材料热力学练习三：各种热力学性质的计算

22:48:11
P
Ml (T1,P1) C
Mv (T2,P2) t
T
22:48:09
纯物质的热力学性质计算
对于均相纯物质，当给定两个强度性质（通常是p，V，T中的 任意两个）后，其他的热力学性质就能计算了，所用模型主 要是状态方程。 纯物质的热力学性质计算，主要计算偏离焓、偏离熵以及逸度 系数等，可借助计算软件ThermalCal进行。 例题3-8（陈新志P46例3-4） 计算异丁烷在400K，2.19MPa 时的压缩因子、偏离焓、偏离熵、逸度系数。
解 ： 三 元 均 相 混 合 物 体 系 的 自 由 度 为 4 ， 给 定 了 T=310.8K ， P=15.2MPa ， y1 = 0.82, y2 = 0.10, y3 = 0.08 后 体 的 质 确 下 了 ， 系 性 就 定 来
计算PR方程常数需要临界参数和偏心因子，查得
临界温度、临界压力和偏心因子 组分（i） 甲烷(1) 氮气(2) 乙烷(3) 计算过程如下：
例题3-9（陈新志P46例3-5 ）试用PR方程计算在200℃、7MPa 下丁烯－1蒸汽的V、H、S。假设0℃的丁烯－1饱和液体的H、S 为零，已知：Tc=419.6K，Pc=4.02MPa，ω=0.187；0℃时丁 烯－1的饱和蒸汽压是Ps=0.1272MPa；
ig CP R =1.967 + 31.63×10−3T − 9.837 ×10−6T 2
T2
∫
1
ig CP P dT − Rln 2 ≈ 22.15J mol-1K-1 (熵 R ) RT P 1 T
T2
∫
1
V2 = 286.41cm 3 mol-1
S(T2 , P ) = 8.314× (−1.6236) − 8.314× (− 9.6202) + 22.15 = 88.63J mol-1K-1 2

1 = V ∂V ∂T P
k
1 ∂V =− V ∂P 。 T
提示：设V=V（T,P）， 求出dV表达式。
解：设V=V（T,P）， ∂V 则dV= ∂T • dT +
P
∂V • dP ∂P T
而β
1 =V
∂V ， ∂T P
②第二dS方程 ②第二dS方程 当S=S(T,P)时， 则dS= + ， 压，不做非体积功W’时， W’ 有 =dH=CpdT, 又由CpdT=TdS+VdP=TdS
而等
(dP=0)
∴dS= 又 =-
,即
=
,
（马氏）
（由dG=-SdT+VdP得到），故有： dS= 第二dS方程
积分有： S-S0=△S= 当为理想气体时： ∵ = =
，而
V ∂T P
，
∴dS= - βVdP （第二dS） dH= CpdT + V (1 − βT )dP （第二dH） 由于k 和β 对于液体而言受压力影响 很小，故常设其为常数，积分时该 常数可以取区间的算术平均值。
CpdT T
3.2.2 剩余（多余）性质法
前面介绍了直接从热力学函数的导 数关系式计算热力学性质，还可使用 多余性质法计算（更为方便）。 （剩）多余性质：气体在真实状态下 的热力学性质与在同样温度、压力下 假设气体处于理想状态下热力学性质 之间的差额。
由Cv=
= ,等容时， 不做W’），
（由dU= + =0，有dU=
又由dU=TdS-PdV= TdS （∵dV=0）
∴Cv= 即 又
= = Cv/T =
=T
,

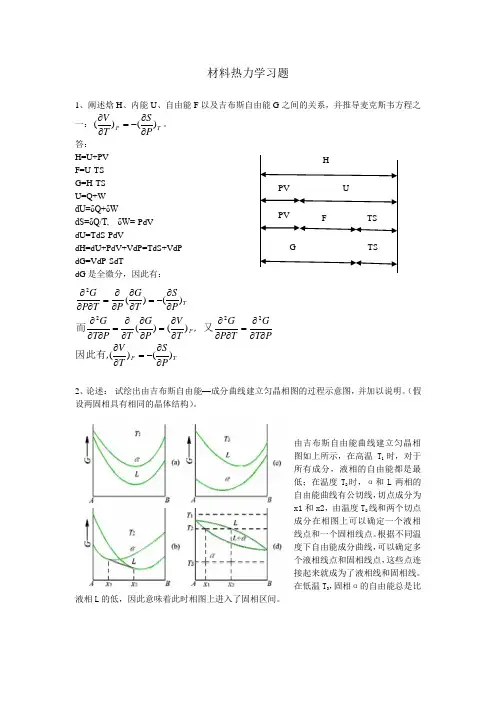
材料热力学习题1、阐述焓H 、内能U 、自由能F 以及吉布斯自由能G 之间的关系，并推导麦克斯韦方程之一：T P PST V )()(∂∂-=∂∂。

答： H=U+PV F=U-TS G=H-TS U=Q+W dU=δQ+δWdS=δQ/T, δW=-PdV dU=TdS-PdVdH=dU+PdV+VdP=TdS+VdP dG=VdP-SdTdG 是全微分，因此有：TP P TP ST V ，PT G T P G ，T V P G T P T G P ST G P T P G )()()()()()(2222∂∂-=∂∂∂∂∂=∂∂∂∂∂=∂∂∂∂=∂∂∂∂∂-=∂∂∂∂=∂∂∂因此有又而2、论述： 试绘出由吉布斯自由能—成分曲线建立匀晶相图的过程示意图，并加以说明。

（假设两固相具有相同的晶体结构）。

由吉布斯自由能曲线建立匀晶相图如上所示，在高温T 1时，对于所有成分，液相的自由能都是最低；在温度T 2时，α和L 两相的自由能曲线有公切线，切点成分为x1和x2，由温度T 2线和两个切点成分在相图上可以确定一个液相线点和一个固相线点。

根据不同温度下自由能成分曲线，可以确定多个液相线点和固相线点，这些点连接起来就成为了液相线和固相线。

在低温T 3，固相α的自由能总是比液相L 的低，因此意味着此时相图上进入了固相区间。

HPV UGTSTS FPV3、论述：通过吉布斯自由能成分曲线阐述脱溶分解中由母相析出第二相的过程。

第二相析出：从过饱和固溶体α中(x0)析出另一种结构的β相(xβ)，母相的浓度变为xα. 即：α→β+ α1α→β+ α1 的相变驱动力ΔGm的计算为ΔGm=Gm(D)-Gm(C)，即图b中的CD段。

图b中EF是指在母相中出现较大为xβ的成分起伏时，由母相α析出第二相的驱动力。

4、根据Boltzman方程S=kLnW，计算高熵合金FeCoNiCuCrAl和FeCoNiCuCrAlTi0.1（即FeCoNiCuCrAl各为1mol，Ti为0.1mol）的摩尔组态熵。

Cu2O (s) + [Fe] = FeO(s) + 2Cu (l) 式中，[ ]表示溶于铜液中。已知 γFeo=19.5。 例题 5-9 已知
问：1）当混合气体（97%H2O + 3%H2, 体积）在 1000 K 是否能将 Ni 氧化？ 2）现有 Ni-Au 固溶体(XNi = 0.1)。已知在 1000 K 时, 与此合金平衡的氢气体体积
例题 6-8 右图所示是铜和铜铝合金(18 at.% Al)在 700℃温度下扩散退火 38.4 天的浓度分
布曲线。求当 Al 的浓度为 4 at%时，Al 在 Cu 中的扩散系数。
18
Cu - Al
Cu
16
A
14
C , at.% Al
12
k
Matano interface
10
8 mark interface
.
材料热力学上课题目
例 1-1 已知液体铅在 1 个大气压下的热容量 Cp(l)为 Cp(l)=32.43-3.10×10-3T J/(mol·k)，固 体铅的热容量 Cp(s)为 Cp(s)=23.56+9.75×10-3T J/(mol·k)，已知液体铅在熔点(600 K)凝固为固 体时放热 4811.60 J/mol，求液体铅过冷至 590K 凝固为固体时焓的变化。
6
4
2
A
1
0 -10 -8 -6 -4 -2 0 2 4 6 8 10
x
六大 板块
第一章 第二章 第三章 第四章 第五章 第六章
物理化学复习纲要
热力学定律（热力学第一定律、热力学第二定律） 自由能（ΔF、ΔG） 热力学状态函数、关系式及应用 相变热力学 溶液 扩散
.

1、由5个粒子所组成的体系，其能级分别为0、ε、2ε及3ε，体系的总能量为3ε。

试分析5个粒子可能出现的分布方式；求出各种分布方式的微观状态数及总微观状态数。

2、有6个可别粒子，分布在4个不同的能级上(ε、2ε、3ε及4ε)，总能量为10ε，各能级的简并度分别为2、2、2、1，计算各类分布的Ωj 及Ω总。

3、振动频率为ν的双原子分子的简谐振动服从量子化的能级规律。

有N 个分子组成玻耳兹曼分布的体系。

求在温度T 时，最低能级上分子数的计算式。

4、气体N 2的转动惯量I =1.394⨯10-46kg ⋅m 2，计算300K 时的Z J 。

5、已知NO 分子的Θυ=2696K ，试求300K 时的Z υ。

~J υ7、计算300K 时，1molHI 振动时对内能和熵的贡献。

8、在298K 及101.3kPa 条件下，1molN 2的Z t 等于多少？9、在300K 时，计算CO 按转动能级的分布，并画出分子在转动能级间的分布曲线。

10、计算H 2及CO 在1000K 时按振动能级的分布，并画出分子在振动能间的分布曲线；再求出分子占基态振动能级的几率。

11、已知HCl 在基态时的平均核间距为1.264⨯10-10m ，振动波数ν~=2990m -1。

计算298K 时的Θm S 。

12、证明1mol 理想气体在101.3kPa 压力下Z t =bLM 3/2(T /K )5/2 (b 为常数)13、计算1molO 2在25︒C 及101.3kPa 条件下的Θm G 、Θm S 及Θm H 。

设Θ0U 等于零。

14、已知300K 时金刚石的定容摩尔热容C V ,m =5.65J ⋅mol -1⋅K -1，求ΘE 及ν。

15．已知300K 时硼的定容摩尔热容C V ,m =10.46J ⋅mol -1⋅K -1，求(1) ΘD ；(2) 温度分别为30K 、50K 、100K 、700K 、1000K 时的C V ,m 值；(3) 作C V ,m 值− T 图形。

4
= 0,∴∆E = 0
Q = ∆ E + W = W = 1 .25 × 10 J
第六章
热力学基础
双原子分子理想气体经过如图的过程， 例 1mol 双原子分子理想气体经过如图的过程，其 为绝热过程、 中1— 2 为直线过程 、2— 3 为绝热过程、3— 1 为等温 过程.已知 T1, T2 = 2T1 , V3 = 8V1 .求：1）各过程的功、 过程 已知 求 ）各过程的功、 热量和内能变化； ）此循环热机效率. 热量和内能变化；2）此循环热机效率 p 解 1): 1— 2
第六章
热力学基础
例：讨论理想气体下图过程中，各过程 讨论理想气体下图过程中，
P A* 1 O 2 绝热 *B V
Q 的正负。
A— B
QAB = 0
WAB = −∆E AB > 0
A— 1— B
QA1B = ∆EAB + WA1B = WA1B −WAB ∵W A1B < W AB ∴ Q A1B < 0
p
A
p=C
解
B
QAB = ∆EAB + WAB
Q AC = W AC
T =C
C
QAD = 0
∵ W AB > W AC > W AD
dQ = 0
D
∆EAB > 0 , ∆EAD < 0
o VA
VB V
∴ Q AB > Q AC > Q AD = 0
第六章
热力学基础
例 一定量理想气体的 图所示， 循环过程如 P－V 图所示， 请填写表格中的空格. 请填写表格中的空格
P A 等温 B
绝热
o
内能增量ΔE/J Δ 0 A→B 过程 B→C C→D D→A ABCD -50 -100 150 50 50 -50 0

热力学练习题全解热力学是研究热能转化和热力学性质的科学，它是物理学和化学的重要分支之一。

在热力学中，我们通过解决一系列练习题来巩固和应用所学知识。

本文将为您解答一些热力学练习题，帮助您更好地理解和应用热力学的基本概念和计算方法。

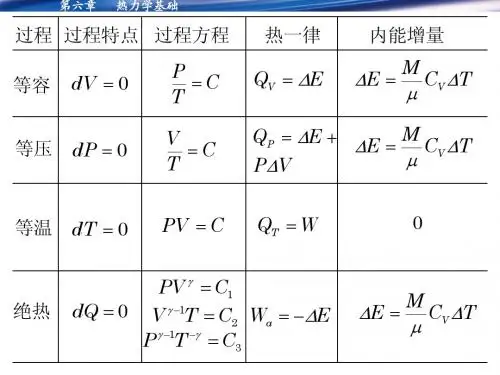
1. 练习题一题目：一个理想气体在等体过程中，吸收了50 J 的热量，对外界做了30 J 的功，求该气体内能的变化量。

解析：根据热力学第一定律，内能变化量等于热量和功之和。

即ΔU = Q - W = 50 J - 30 J = 20 J。

2. 练习题二题目：一摩尔理想气体从A状态经过两个等温过程和一段绝热过程转变为B状态，A状态和B状态的压强和体积分别为P₁、P₂和V₁、V₂，已知 P₂ = 4P₁，V₁ = 2V₂，求这个过程中气体对外界做的总功。

解析：由两个等温过程可知，气体对外界做的总功等于两个等温过程的功之和。

即 W = W₁ + W₂。

根据绝热过程的特性，绝热过程中气体对外做功为零。

因此，只需要计算两个等温过程的功即可。

根据理想气体的状态方程 PV = nRT，结合已知条件可得：P₁V₁ = nRT₁①P₂V₂ = nRT₂②又已知 P₂ = 4P₁，V₁ = 2V₂，代入式①和式②可得：8P₁V₂ = nRT₁③4P₁V₂ = nRT₂④将式③和式④相减，可得：4P₁V₂ = nR(T₁ - T₂) ⑤由于这两个等温过程温度相等，即 T₁ = T₂，代入式⑤可得：4P₁V₂ = 0所以，这个过程中气体对外界做的总功 W = 0 J。

通过以上两个练习题的解答，我们可以看到在热力学中，我们通过应用热力学第一定律和理想气体的状态方程等基本原理，可以解答各种热力学问题。

熟练掌握这些计算方法，有助于我们更深入地理解热力学的基本概念，并应用于实际问题的解决中。

总结：本文对两道热力学练习题进行了详细解答，分别涉及了等体过程和等温过程。

通过这些例题的解析，读者可以理解和掌握热力学的基本计算方法，并将其应用于实际问题的求解中。

高中物理热力学问题中的热容和热功的计算方法热力学是物理学中的一个重要分支，研究物质在热平衡状态下的性质和相互关系。

在高中物理中，热力学是一个重要的考点，其中热容和热功的计算方法是学生们经常遇到的难点。

本文将详细介绍热容和热功的计算方法，并通过具体题目举例，帮助读者更好地理解和应用这些知识。

一、热容的计算方法热容是物质吸收或释放单位温度变化时所吸收或释放的热量。

具体计算方法如下：1. 对于固体和液体物质，热容可以通过以下公式计算：Q = mcΔT其中，Q是物质吸收或释放的热量，m是物质的质量，c是物质的比热容，ΔT是温度变化。

2. 对于气体物质，热容的计算方法略有不同。

在等压条件下，热容可以通过以下公式计算：Q = nCpΔT其中，Q是物质吸收或释放的热量，n是物质的摩尔数，Cp是物质的摩尔热容，ΔT是温度变化。

举例说明：假设有一块质量为0.5kg的铁块，其初始温度为20℃，加热后的最终温度为80℃。

已知铁的比热容为450J/(kg·℃)，求铁块吸收的热量。

解析：根据热容的计算方法，可以使用公式Q = mcΔT来计算。

代入已知条件，得到：Q = 0.5kg × 450J/(kg·℃) × (80℃ - 20℃) = 13500J因此，铁块吸收的热量为13500J。

二、热功的计算方法热功是物质通过热量传递做的功。

具体计算方法如下：1. 对于等容过程，热功可以通过以下公式计算：W = 02. 对于等压过程，热功可以通过以下公式计算：W = PΔV其中，W是热功，P是压强，ΔV是体积变化。

3. 对于绝热过程，热功可以通过以下公式计算：W = Q其中，W是热功，Q是吸收或释放的热量。

举例说明：假设有一摩尔的理想气体，初始体积为V1，初始压强为P1，最终体积为V2，最终压强为P2。

已知该过程是等压过程，求气体所做的热功。

解析：根据热功的计算方法，可以使用公式W = PΔV来计算。

T2
∫
1
ig CP P dT − Rln 2 ≈ 22.15J mol-1K-1 (熵 R ) RT P 1 T
T2
∫
1
V2 = 286.41cm 3 mol-1
S(T2 , P ) = 8.314× (−1.6236) − 8.314× (− 9.6202) + 22.15 = 88.63J mol-1K-1 2
性 质
V v / cm3mol −1
T = 400 K，P = 2.19 MPa， 气相 PR 方 程 三参 数对 态原 应 理 6 a =1461372 MPa cm mol-2， = 72.35675 cm mol-1 b 3 （ 例题5）
1080.85 0.7117 -0.9107 -0.6497 -0.2610
∫
22:48:11
例题3-5（续）
= S(T2 , P ) − Sig (T2 , P ) − S(T , P ) − Sig (T , P ) + Sig (T2 , P ) − Sig (T , P ) 2 2 1 1 1 1 2 1 1
T
S(T2 , P ) = S(T2 , P ) − S(T , P ) 2 2 1 1
T
H(T2 , P ) = H(T2 , P ) − H(T , P ) 2 2 1 1
[
] [
] [
]
2 ig H(T2 , P ) − Hig (T2 ) H(T , P ) − Hig (T ) CP 2 1 1 1 = RT2 − RT dT +R 1 RT2 RT R 1 T 1
22:48:11
例题3-10（陈新志P49例3-6） 混合物性质计算

材料热力学习题答案
材料热力学学习题答案
热力学是物理学的一个重要分支，研究物质的热量和能量转化规律。

在学习热
力学的过程中，我们常常会遇到各种各样的学习题，通过解答这些学习题，我
们可以更好地理解热力学的知识，提高自己的学习能力。

1. 热力学第一定律是什么？请用数学公式表示。

答案：热力学第一定律是能量守恒定律，即能量不会自发地产生或消失，只能
从一种形式转化为另一种形式。

数学公式表示为ΔU = Q - W，其中ΔU表示系
统内能的变化，Q表示系统吸收的热量，W表示系统对外做功。

2. 什么是热容？如何计算物质的热容？
答案：热容是物质单位质量在单位温度变化下吸收或释放的热量。

物质的热容
可以通过公式C = Q/mΔT来计算，其中C表示热容，Q表示吸收或释放的热量，m表示物质的质量，ΔT表示温度变化。

3. 什么是热力学循环？请举例说明一个热力学循环的应用。

答案：热力学循环是指一定物质在一定压力下，经过一系列的热力学过程后，
最终回到初始状态的过程。

一个常见的热力学循环是卡诺循环，它被广泛应用
于蒸汽发电厂和制冷系统中。

通过解答这些学习题，我们可以更加深入地理解热力学的知识，掌握热力学的
基本原理和计算方法。

希望大家在学习热力学的过程中能够勤加练习，提高自
己的学习能力，为将来的科学研究和工程实践打下坚实的基础。

材料热力学试题_参考答案 (2007年)一、填空题（每题5分，共10分）1. 0≥m dS 作为过程的可逆性判据，其适用条件是 绝热或隔离体系 。

2. 热力学基本方程Vdp SdT dG +-=的适用条件是 只作体积功的封闭体系 。

二、简答题 (本题20分，每小题10分)1. 平衡态的判据（即判断某一过程是否能自发进行）有哪几个？哪一个最广泛地在实践中被运用？为什么？（10分）[答] (1) 熵(S)判据（ dS ≥0 ）；(2) 恒温恒容且只作体积功的亥姆霍兹(Helmholtz)自由能判据：自发过程dF <0，平衡过程dF=0 ；(3) 恒温恒压且只作体积功的的吉布斯(Gibbs)自由能判据：自发过程dG <0，平衡过程dG=0。

吉布斯(Gibbs)自由能判据最广泛地被运用。

因为绝大多数的实际过程发生在恒温恒压的条件下。

2. 简述马氏体相变的特点。

并举一实例说明其在具体实践中应用。

（10分）[答] 马氏体相变的特点有：马氏体相变是无扩散相变之一，原子只做有规则的重排（集团式变位）而不进行扩散；(2) 马氏体沿惯习（析）面生长并与奥氏体母相保持一定的取向关系，形成共格晶界；(3) 马氏体相变发生在一定的温度区间内(M s ~M f )；(4) 马氏体相变的可逆性；(5) 快速长大；(6) 马氏体转变的不完全性。

实例1：刀具通过锋刄的高温局部淬火，可达到强度和韧性的结合；实例2：通过高温淬火生产弹簧。

三、计算题（共40分）1. Al 在Fcc 结构时的摩尔吉布斯自由能为G Fcc_A1：-7976.15 + 137.093T - 24.3672 T lnT - 1.88466 T 2×10–3 - 8.7766 T 3×10–7 + 74092 T –1 (298.15<T<700) 计算300K ，500K 时Al 的Cp 值，S 值以及H 值。

热力学习题及答案解析
热力学学习题及答案解析
热力学是物理学的一个重要分支，研究能量转化和热力学系统的性质。

在学习
热力学的过程中，我们经常会遇到各种热力学学习题，通过解题可以加深对热
力学知识的理解。

下面我们就来看看一些常见的热力学学习题及答案解析。

1. 问题：一个理想气体在等温过程中，体积从V1扩大到V2，求气体对外界所
做的功。

答案解析：在等温过程中，理想气体对外界所做的功可以用以下公式表示：
W = nRTln(V2/V1)，其中n为气体的摩尔数，R为气体常数，T为温度。

根据这
个公式，我们可以计算出气体对外界所做的功。

2. 问题：一个物体从20摄氏度加热到80摄氏度，求其温度变化时吸收的热量。

答案解析：物体温度变化时吸收的热量可以用以下公式表示：Q = mcΔT，其
中m为物体的质量，c为物体的比热容，ΔT为温度变化。

根据这个公式，我们
可以计算出物体温度变化时吸收的热量。

3. 问题：一个热机从高温热源吸收了500J的热量，向低温热源放出了300J的
热量，求该热机的热效率。

答案解析：热机的热效率可以用以下公式表示：η = 1 - Q2/Q1，其中Q1为
热机从高温热源吸收的热量，Q2为热机向低温热源放出的热量。

根据这个公式，我们可以计算出该热机的热效率。

通过以上几个热力学学习题及答案解析，我们可以看到在解题的过程中，需要
灵活运用热力学知识，并且掌握一定的计算方法。

希望通过不断的练习和思考，我们能够更好地理解和掌握热力学知识，提高解题能力。

解：（1）可逆膨胀
S
(体系）
(
Q T
)R

Wmax T
nR ln V2 V1
nR ln10 19.14 J K1
S（隔离） S（体系） S（环境） 0 （1）为可逆过程。
上一内容 下一内容 回主目录
返回
2020/2/27
等温过程的熵变
（2）真空膨胀 熵是状态函数，始终态相同，体系熵变也相同，
返回
2020/2/27
变温过程的熵变
(3)物质的量一定从 p1,V1,T1 到 p2 ,V2 ,T2的过程。这种情 况一步无法计算，要分两步计算，有三种分步方法：
1. 先等温后等容 2. 先等温后等压
S nR ln(V2 ) T2 nCV ,mdT
V1
T1
T
S nR ln( p1 ) T2 nCp,mdT
r Sm$ (T ) r Sm$ (298.15K)
T 298.15K
BCp,m (B)dT
B
T
上一内容 下一内容 回主目录
返回
2020/2/27
化学过程的熵变
(3)在298.15 K时，求反应压力为p时的熵变。标准压 力下的熵变值查表可得
r Sm ( p) rSm$ ( p$ )
上一内容 下一内容 回主目录
返回
2020/2/27
等温过程的熵变
例3：在273 K时，将一个22.4 dm3 的盒子用隔板一分为
二，一边放 0.5 mol O，2 (另g)一边放
0.5 mo。l N2 (g)
求抽去隔板后，两种气体混合过程的熵变？
解法1：
S(O2 )

化学热力学计算题练习了解热力学计算的基本公式和应用熟练计算焓变熵变和自由能变化化学热力学计算题练习了解热力学计算的基本公式和应用熟练计算焓变、熵变和自由能变化热力学是研究能量转化和能量传递规律的科学。

在化学领域中，热力学是研究化学反应的热效应和理论基础。

在化学研究和实践中，准确计算焓变、熵变和自由能变化是十分重要的。

本文将介绍热力学计算的基本公式，并通过练习来加深对这些公式的应用和理解。

热力学计算的基本公式如下：1. 焓变（ΔH）的计算公式：ΔH = H(产物) - H(反应物)其中，ΔH代表焓变，H代表焓。

2. 熵变（ΔS）的计算公式：ΔS = S(产物) - S(反应物)其中，ΔS代表熵变，S代表熵。

3. 自由能变化（ΔG）的计算公式：ΔG = ΔH - TΔS其中，ΔG代表自由能变化，ΔH代表焓变，T代表温度，ΔS代表熵变。

下面通过计算题来加深对这些公式的应用：题目一：某化学反应的焓变为-100 kJ，熵变为200 J/K，求在298 K下的自由能变化。

解答：将所给数据代入自由能变化的计算公式中，可以得到：ΔG = ΔH - TΔS= -100 kJ - 298 K × (0.2 kJ/K)= -100 kJ - 59.6 kJ= -159.6 kJ所以，在298 K下，该化学反应的自由能变化为-159.6 kJ。

题目二：某化学反应的焓变为50 kJ，自由能变化为-20 kJ，求在298 K下的熵变。

解答：将所给数据代入熵变的计算公式中，可以得到：ΔG = ΔH - TΔS-20 kJ = 50 kJ - 298 K × ΔSΔS = (50 kJ + 20 kJ) / 298 K= 0.23 kJ/K所以，在298 K下，该化学反应的熵变为0.23 kJ/K。

根据以上两个计算题的练习，我们可以发现，在热力学计算中，焓变、熵变和自由能变化之间存在着密切的关系。

而通过掌握基本的计算公式，能够准确计算出化学反应的焓变、熵变和自由能变化，进而对化学反应的热效应及反应性质进行分析和判断。

热力学计算题型热力学是研究能量转化和热力学性质的分支学科，是物理学、化学等自然科学领域重要的基础知识。

在学习热力学的过程中，我们经常会遇到一些计算题型，通过这些题目的解答，可以加深对热力学原理的理解。

本文将就几个常见的热力学计算题型进行探讨，希望能对读者有所启发。

首先，让我们来看一个热机效率的计算题。

热机效率是指热机从燃料中吸收的热量与输出的有用功之比，通常通过下面的公式来表示:η = 1 - (Tc/Th)其中，η表示热机效率，Tc表示热机的工作温度，Th表示热机吸收热量的温度。

通过这个公式，我们可以很方便地计算热机的效率。

例如，一个热机的工作温度为300K，吸收热量的温度为1000K，则根据上述公式，可以计算出该热机的效率为70%。

接下来，我们来看一个常见的焓变计算题。

焓变是指在恒压条件下，物质在化学反应过程中吸收或释放的热量。

根据热力学第一定律，焓变等于系统的内能变化与对外做功之和。

公式如下：ΔH = ΔE + PΔV其中，ΔH表示焓变，ΔE表示内能变化，P表示压强，ΔV表示体积的变化。

通过这个公式，我们可以计算出化学反应的焓变。

例如，若某化学反应在1 atm和298K下进行，反应体系的初始体积为2L，最终体积为1L，内能的变化为-500 J，代入上述公式，可以计算出焓变为-500 J。

另外，还有一个常见的热力学计算题是计算熵变。

熵是描述系统无序程度的物理量，在热力学中起着重要的作用。

对于一个可逆过程，熵变可以通过下面的公式计算：ΔS = Q / T其中，ΔS表示熵变，Q表示系统吸收或释放的热量，T表示系统的温度。

通过这个公式，我们可以计算出系统的熵变。

例如，若某系统吸收了200 J的热量，并且温度保持恒定为300 K，代入上述公式，可以计算出系统的熵变为200 J/300 K。

最后，让我们来看一个热力学计算题中的综合问题。

假设某系统的焓变为1000 J，熵变为200 J/K，求该系统的自由能变化。

材料热力学习题答案材料热力学习题答案热力学是研究物质的能量转化和能量传递规律的科学。

在材料科学中，热力学是一个重要的分支，它可以帮助我们理解材料在不同条件下的性质和行为。

在学习热力学的过程中，我们经常会遇到一些习题，下面我将给出一些常见材料热力学习题的答案。

1. 问题：在常压下，将1mol的水从25℃加热到100℃，需要吸收多少热量？答案：要计算这个问题，我们可以使用热容的概念。

热容是物质在单位温度变化下吸收或释放的热量。

对于水来说，其热容为4.18J/(g℃)。

首先，我们需要知道水的质量，由于1mol的水的摩尔质量为18g/mol，因此1mol的水的质量为18g。

接下来，我们需要计算水的温度变化，即100℃-25℃=75℃。

最后，我们可以使用公式Q=mCΔT来计算所需吸收的热量，其中Q是热量，m是质量，C是热容，ΔT是温度变化。

代入数值得到Q=18g×4.18J/(g℃)×75℃=5613J。

2. 问题：在恒定温度下，气体的体积与压力之间的关系是什么？答案：根据热力学的理论，理想气体的体积与压力成反比。

这可以用理想气体状态方程PV=nRT来解释，其中P是压力，V是体积，n是物质的摩尔数，R是气体常数，T是温度。

根据这个方程，当温度保持不变时，如果压力增加，体积将减小，反之亦然。

这种关系被称为波义尔定律。

3. 问题：在材料科学中，什么是熵？答案：熵是热力学中的一个重要概念，它用于描述物质的无序程度。

熵可以理解为系统的混乱程度或无序程度。

根据热力学的第二定律，系统的熵总是趋向于增加，即系统总是朝着更高的熵状态发展。

当物质从有序状态转变为无序状态时，熵会增加。

例如，当固体融化成液体，或者液体蒸发成气体时，系统的熵会增加。

熵在材料科学中起着重要的作用，可以帮助我们理解材料的相变行为和稳定性。

4. 问题：什么是自由能？答案：自由能是热力学中另一个重要的概念，它用于描述系统的稳定性和可逆性。

热力学中的热平衡与热力学函数练习题及解答热力学中的热平衡与热力学函数练习题及解答1. 简答题(1) 什么是热平衡？热平衡是指在一个封闭系统中，不同部分之间没有温度差异或温度差异可以被忽略的状态。

在热平衡状态下，系统内部没有净热流动，也就是热量的输入和输出是平衡的。

(2) 什么是热力学函数？热力学函数是用来描述热力学系统特性的函数。

热力学函数包括内能、焓、自由能和吉布斯自由能等。

(3) 内能与焓有何区别？内能是指系统中所有微观粒子的总能量，包括其动能和势能。

焓是内能和系统对外做功之和，因此焓是表示系统实际能量的一个重要指标。

2. 计算题(1) 一定质量的水在常压下被加热，当水的温度升高到100℃时，是否出现相变？为什么？在常压下，当水的温度升高到100℃时，会发生相变，从液态变为气态。

这是因为在常压下，水达到100℃时饱和蒸气压与大气压相等，此时水开始沸腾，液态水分子脱离液面转变为水蒸气。

(2) 一个理想气体的体积与温度之间的关系可以用理想气体状态方程 PV=nRT 表示，在等体积条件下温度变化为ΔT，计算气体内能的变化ΔU。

在等体积条件下，内能的变化等于系统吸收的热量，即ΔU = Q。

根据理想气体状态方程 PV=nRT，可以得到 PV/T = nR，其中 n、R为常数。

将初始状态和最终状态的方程代入，并化简，得到 (P1V1/T1) -(P2V2/T2) = 0。

由于等体积条件下体积不变，因此 V1=V2，代入上式得到 (P1/T1) - (P2/T2) = 0。

可以进一步化简为 (P1/T1) = (P2/T2) ，即 P1/T1 = P2/T2。

因此，对于等体积条件下，气体内能的变化ΔU = 0。

3. 论述题热力学函数在热平衡条件下的应用热力学函数在热平衡条件下起到了重要的作用。

在热平衡状态下，系统的温度不变，因此可以使用温度表示热力学函数的变化。

以下以内能和焓为例进行论述。

热平衡条件下，内能的变化仅与系统吸收或放出的热量有关。