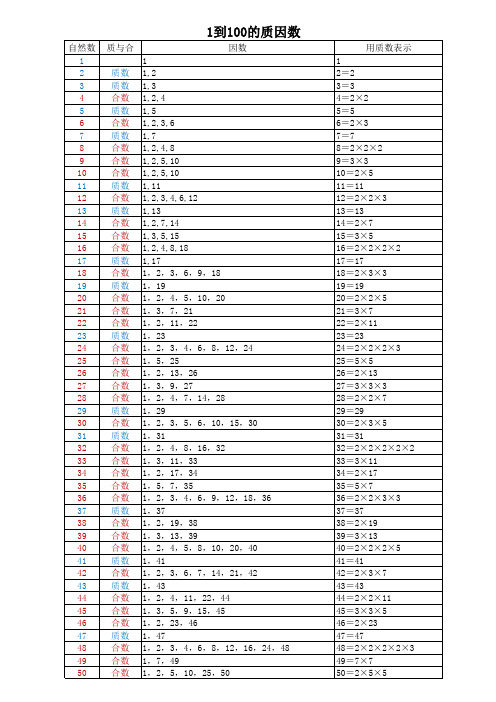
1到100以内的质数表
- 格式:docx
- 大小:37.05 KB
- 文档页数:2

100以内的质数表口诀100以内的质数表口诀一:
二、三、五、七、一十一(2、3、5、7、11);
十三、十七、一十九(13、17、19);
二三九、三一七(23、29、31、37);
五三九、六一七(53、59、61、67);
四一三七、七一三九(41、43、47、71、73、79);八三、八九、九十七(83、89、97)。
质数表口诀二:
二、三、五、七和十一;
十三后面是十七;
十九、二三、二十九;
三一、三七、四十一;
四三、四七、五十三;
五九、六一、六十七;
七一、七三、七十九;
八三、八九、九十七。
质数表口诀三:
二、三、五、七、一十一;
一三、一九、一十七;
二三、二九、三十七;
三一、四一、四十七;
四三、五三、五十九;
六一、七一、六十七;
七三、八三、八十九;
再加七九、九十七;
25个质数不能少;
百以内质数心中记。
质数表口诀四:
二哥独行无偶伴,三五七九十一显。
十三十五十七连,十九廿三在后边。
廿九三十一只差一,三十一来接龙戏。
三十七过四十一,四十三与四十七齐。
五十已过看五十三,五十九紧贴六十一。
六十七前有六十一,七十一后跟七十三。
七十九八十三并肩,八十九后面九十一位空。
百以内最后两质数,八十九、九十七唱压轴。


100以内的质数:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97。
定义编辑质数又称素数。
一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数。
质数性质编辑质数的个数是无穷的。
欧几里得的《几何原本》中有一个经典的证明。
它使用了证明常用的方法:反证法。
具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,p n,设N=p1×p2×……×p n,那么,是素数或者不是素数。
如果为素数,则要大于p1,p2,……,p n,所以它不在那些假设的素数集合中。
1、如果为合数,因为任何一个合数都可以分解为几个素数的积;而N和N+1的最大公约数是1,所以不可能被p1,p2,……,p n整除,所以该合数分解得到的素因数肯定不在假设的素数集合中。
因此无论该数是素数还是合数,都意味着在假设的有限个素数之外还存在着其他素数。
所以原先的假设不成立。
也就是说,素数有无穷多个。
2、其他数学家给出了一些不同的证明。
欧拉利用黎曼函数证明了全部素数的倒数之和是发散的,恩斯特·库默的证明更为简洁,哈里·弗斯滕伯格则用拓扑学加以证明。
记忆方法:100以内的质数共有25个,这些质数我们经常用到,可以用下面的两种办法记住它们。
一、规律记忆法首先记住2和3,而2和3两个质数的乘积为6。
100以内的质数,一般都在6的倍数前、后来的位置上。
如5、7、11、13、19、23、29、31、37、41、43……只有25、35、49、55、65、77、85、91、95这几个6的倍数前后位置上的数不是质数,而这几个数都是5或7的倍数。
由此可知:100以内6的倍数前、后位置上的两个数,只要不是5或7的倍数,就一定是质数。
根据这个特点可以记住100以内的质数。
二、分自类记忆法我们可以把100以内的质数分为五类记忆。

100以内的素数(质数)表
2、3、5、7
11、13、17、19
23、29
31、37
41、43、47
53、59
61、67
;
71、73、79
83、89
97
推荐两种记忆方法,可以把两种方法结合起来(找到素数表中相似的部分)。
(一)口诀:
二、三、五、七、一十一,(表示:2、3、5、7、11)
十三、十七、一十九。
(表示:13、17、19)
二三九,三一七,(表示:23、29、31、37)
—
五三九,六一七。
(表示:53、59、61、67)
四一三七,七一三九,(表示:41、43、47、71、73、79)
八三八九,九十七。
(表示:83、89、97)
(二)按“3的倍数”的相似特点。
在“3的倍数”中,如5□可以填1、4、7;
1□可以填2、5、8;3□可以填0、3、6、9。
也就是把数分成了三部分来记忆:
、
(1) 11、13、17、19(一十几)
41、43、47(四十几)
71、73、79(七十几)
(2) 23、29(二十几)
53、59(五十几)
83、89(八十几)
(3) 31、37(三十几)
61、67(六十几)
|
97(九十几)
(三)素数的个数:
20以内素数有8个,50以内素数有15个,100以内素数有25个。

100以内的质数表质数表100以内有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。
100以内的质数共有25个,质数的分布规律是以36N(N+1)为单位,随着N的增大,素数的个数以波浪形式渐渐增多。
质数表可用顺口溜来记:—位质数偶打头,2、3、5、7要记熟;两位质数不用愁,可以编成顺口溜。
十位若是4和1,个位准有1、3、7; 十位若是2、5、8,个位3、9往上加;十位若是3和6,个位1、7跟在后;十位若是被7占,个位准是1、9、3;19、97最后算。
什么是质数质数也叫质数。
大于1的自然数,除了1和它本身,叫做质数。
质数的数量是无限的。
100以内的质数规律规律一:看区间质数的个数以10个数为一个区间看质数的个数,呈4,4,2,2,3,2,2,3,2,1规律。
规律二:看每个质数的个位数100以内的质数个位数有以下几种:1,2,3,5,7,9,共6种情况。
规律三:看区间有2或3个质数的个位数区间有2个质数的个位数规律为:3,9,或1,7区间有3个质数的个位数规律为:1,3,7或1,3,9100以内有25个质数,你可以自己想办法记。
探究判断质数的方法课本例1提供了一个方法,依次划掉某些数的倍数,把不是质数的都排除了,剩下的就都是质数。
依次划掉2、3的倍数后(2、3除外),接下来应该划掉几的倍数呢?当然不是4!上课认真听讲的同学都知道,接下来只需把5、7的倍数划掉就可以了(5、7除外)。
原理简析:由合数的意义可知,只要判断一个数除了1和它本身还有别的因数,这个数就是合数。
因为因数是成对出现的,所以只要判断前一半即可。
10^2=100,而10以内的质数只有2、3、5、7,所以只要划掉2、3、5、7的倍数即可(2、3、5、7除外)。
重点来了!2、5的倍数一眼就能看出,3的倍数只需计算数字和(1位数+1位数),7的倍数除去2、3、5的倍数及九九表内的数,只剩下77和91,而77又可以一眼看出是合数,所以只剩一个数——91!简单总结一下:100以内除了91,个位数都是1、3、7、9,位数和不是3倍数的都是质数。
1到100以内的质数表
1到100以内的质数表
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
质数,也称为素数,是指大于1且只能被1和自身整除的正整数。
质
数在数学中扮演重要的角色,具有许多独特的性质和应用。
以下是1
到100之间的质数表。
2是最小的质数,同时也是唯一一个偶数质数。
接下来的几个质数是3、5和7。
3是最小的奇数质数,5是最小的奇数的平方并且不是平方的质数,7是最小的不是三角形数或五边形数的质数。
然后是11、13和17,这些质数在十位数上都是1或3,并且它们与奇
数质数的特性相似。
紧随其后的是19,这个质数在个位数上是9的倍
数加上2。
接下来的几个质数是23、29和31,它们有着不同的特点。
23是一个
两位数中以3结尾的质数,29是不同两位数的正质数,而31是一个与
其他两位数质数拥有共同特性的例子。
在接下来的质数表中,我们看到37、41、43和47这些质数都是在个
位数上以7结尾。
接下来的质数是53、59和61,它们在十位数上是5
或6,并表现出了与之前类似的特性。
67是接下来的质数,它是一个以7结尾的两位数质数。
71是一个以1
结尾的质数,73则是一个以3结尾的质数。
79是一个以9结尾的质数,并且它是79和89之间唯一以9结尾的质数。
83和89是两位数质数中的最后两个。
它们都不是以7结尾,并且显示
出了特定的属性。
最后,97是100以内的最大质数,是一个以7结尾
的质数,同时也是唯一一个以7结尾的两位数质数。
通过这个质数表,我们可以看到1到100之间的质数分布的规律和特性。
这些质数在数论和其他领域中具有广泛的应用,例如密码学、因
式分解等。
对质数的理解对于深入研究数学和相关学科是非常重要的。
质数表是数学中的一项基础工具,帮助我们更好地理解数字之间的关
系和模式。
通过研究质数,我们可以探索数学的奥妙,并应用于实际
问题的解决中。
所以,对于数学爱好者和学生来说,研究和记忆质数
表是一个非常有益的练习。
总结起来,1到100以内的质数表对于数学爱好者来说是一个有趣且有
用的工具。
通过研究质数表,我们可以深入了解质数的特性和模式,
同时也能够更好地理解数学中的各种概念和应用。