四川省2017届高三上学期巴蜀黄金大联考试题 理科数学 Word版含答案

四川省2017-2018学年高三巴蜀黄金大联考理科综合能力测试卷考生注意：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共300分，考试时间150分钟。

2．请将各题答案填在试卷后面的答题卡上。

3．可能用到的相对原子质量：H 1 N 14 O 16 Na 23 Al 27 S 32 Cu 64第Ⅰ卷（选择题共126分）一、选择题：本大题共共13小题，每小题6分。

在每给出的四个选项中，只有一项符合题目要求的。

1．下列有关细胞结构与功能的叙述中，正确的是A. 高尔基体是细胞内的“脂肪合成车间”B. 溶酶体能合成水解酶用于分解衰老的细胞器C. 中心体在动物细胞有丝分裂的前期完成倍增D. 细胞液浓度大于外界浓度，植物细胞发生质壁分离2．有关物质运输方式的叙述中,正确的是A. 无机盐离子进出细胞的方式均为主动运输B. mRNA从核孔到达细胞质,该过程需要消耗能量C. 被动运输都是顺浓度梯度进行的,不需要载体和能量D. 分泌蛋白分泌到细胞外的过程主要体现细胞膜的选择透过性3．研究发现,正常干细胞中两种关键蛋白质“失控”发生越位碰撞后,正常干细胞会变成肿瘤干细胞.下列有关说法错误的是A. 干细胞的分化方向与细胞中基因的执行情况有关B. 干细胞具有控制该种生物生长发育的全套遗传物质C. 干细胞分化后的细胞凋亡是由基因决定的D. 干细胞在癌变过程中细胞膜上的甲胎蛋白会减少4．下列实验材料、用具和方法的改变，对实验结果影响最大的是A. 用纤维素酶处理过的植物细胞代替未处理的植物细胞做质壁分离实验B. 用丙酮代替无水酒精进行叶绿体色素的提取C. 用大蒜根尖代替洋葱根尖观察植物细胞有丝分裂D. 用低温代替秋水仙素处理萌发的种子以诱导染色体数目加倍5．苦瓜植株中含一对等位基因D和d，其中D基因纯合的植株不能产生卵细胞，而e基因纯合的植株花粉不能正常发育，杂合子植株完全正常。

现有基因型为Dd的苦瓜植株若干做亲本，下列有关叙述错误的是A．如果每代均自交直至F2，则F2植株中d基因的频率为1/2B．如果每代均自交直至F2，则F2植株中正常植株所占比例为1/2C．如果每代均自由交配直至F2，则F2植株中D基因的频率为1/2D．如果每代均自由交配直至F2，则F2植株中正常植株所占比例为1/26．如图为某细胞一个DNA 分子中a 、b 、c 三个基因的分布状况,图中I 、Ⅱ为无遗传效应的序列.有关叙述正确的是A. 该DNA 片段中含有3个起始密码子B. 片段中a 基因整体缺失,该变异属于染色体结构变异C. 若c 中碱基对发生改变,则性状不一定会发生改变D. 在四分体时期,b 、c 之间可能发生交叉互换7. 化学与人类生产、生活密切相关,下列有关说法正确的是A. 浓硫酸具有吸水性，可作食品干燥剂B. 夏天雷雨过后感觉到空气清新是因为产生了少量2NOC. 缤纷绚丽的烟花中添加了含钾、钠、钙、铜等金属元素的化合物D. 明矾可以使海水淡化，从而解决“淡水供应危机”8. 氢化铝钠由于具有储氢性能而备受关注，它可用氢化物、铝、高压氢在烃或醚溶剂中反应制得：422322N a A l H H Al NaH =++。

2017年四川省省级联考高考数学模拟试卷（理科）一、选择题：本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知i是虚数单位，复数（2+i）2的共轭复数为（）A．3﹣4i B．3+4i C．5﹣4i D．5+4i2．设向量=（2x﹣1，3），向量=（1，﹣1），若⊥，则实数x的值为（）A．﹣1 B．1 C．2 D．33．设集合A={﹣1，1}，集合B={x|ax=1，a∈R}，则使得B⊆A的a的所有取值构成的集合是（）A．{0，1}B．{0，﹣1} C．{1，﹣1} D．{﹣1，0，1}4．执行如图所示的程序框图，输出S的值为（）A．45 B．55 C．66 D．1105．小孔家有爷爷、奶奶、姥爷、姥姥、爸爸、妈妈，包括他共7人，一天爸爸从果园里摘了7个大小不同的梨，给家里每人一个，小孔拿了最小的一个，爷爷、奶奶、姥爷、姥姥4位老人之一拿最大的一个，则梨子的不同分法共有（）A．96种B．120种C．480种D．720种6．函数的部分图象如图所示，则函数f（x）的解析式为（）A．B．C．D．7．设直角坐标平面内与两个定点A（﹣2，0），B（2，0）的距离之差的绝对值等于2的点的轨迹是E，C是轨迹E上一点，直线BC垂直于x轴，则=（）A．﹣9 B．﹣3 C．3 D．98．利用计算机产生120个随机正整数，其最高位数字（如：34的最高位数字为3，567的最高位数字为5）的频数分布图如图所示，若从这120个正整数中任意取出一个，设其最高位数字为d（d=1，2，…，9）的概率为P，下列选项中，最能反映P与d的关系的是（）A．P=lg（1+）B．P=C．P=D．P=×9．如图，A1，A2为椭圆+=1的长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS，OT围成一个平行四边形OPQR，则|OS|2+|OT|2=（）A．5 B．3+C．9 D．1410．设a，b是不相等的两个正数，且blna﹣alnb=a﹣b，给出下列结论：①a+b﹣ab＞1；②a+b＞2；③ +＞2．其中所有正确结论的序号是（）A．①② B．①③ C．②③ D．①②③二、填空题（每题5分，满分25分，将答案填在答题纸上）11．在（2﹣）6的展开式中，含x3项的系数是（用数字填写答案）12．一个几何体的三视图如图所示，则几何体的体积为．13．已知tanα=3，则sinαsin（﹣α）的值是．14．已知圆的方程为x2+y2﹣6x=0，过点（1，2）的该圆的三条弦的长a1，a2，a3构成等差数列，则数列a1，a2，a3的公差的最大值是．15．已知=（1，0），=（1，1），（x，y）=，若0≤λ≤1≤μ≤2时，z=+（m＞0，n＞0）的最大值为2，则m+n的最小值为．三、解答题（本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.）16．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足acosB=bcosA．（1）判断△ABC的形状；（2）求sin（2A+）﹣2cos2B的取值范围．=+2a n（n∈N*）17．设数列{a n}各项为正数，且a2=4a1，a n+1（I）证明：数列{log3（1+a n）}为等比数列；），数列{b n}的前n项和为T n，求使T n＞345成立时n的最小值．（Ⅱ）令b n=log3（1+a2n﹣118．某商场进行有奖促销活动，顾客购物每满500元，可选择返回50元现金或参加一次抽奖，抽奖规则如下：从1个装有6个白球、4个红球的箱子中任摸一球，摸到红球就可获得100元现金奖励，假设顾客抽奖的结果相互独立．（Ⅰ）若顾客选择参加一次抽奖，求他获得100元现金奖励的概率；（Ⅱ）某顾客已购物1500元，作为商场经理，是希望顾客直接选择返回150元现金，还是选择参加3次抽奖？说明理由；（Ⅲ）若顾客参加10次抽奖，则最有可能获得多少现金奖励？19．如图，在正方形ABCD中，点E，F分别是AB，BC的中点．将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．（1）求证：平面PBD⊥平面BFDE；（2）求二面角P﹣DE﹣F的余弦值．20．已知直线l的方程为y=x+2，点P是抛物线y2=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y2=4x 交于点B．（Ⅰ）求点P的坐标；（Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．21．设a，b∈R，函数，g（x）=e x（e为自然对数的底数），且函数f（x）的图象与函数g（x）的图象在x=0处有公共的切线．（Ⅰ）求b的值；（Ⅱ）讨论函数f（x）的单调性；（Ⅲ）若g（x）＞f（x）在区间（﹣∞，0）内恒成立，求a的取值范围．2017年四川省省级联考高考数学模拟试卷（理科）参考答案与试题解析一、选择题：本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知i是虚数单位，复数（2+i）2的共轭复数为（）A．3﹣4i B．3+4i C．5﹣4i D．5+4i【考点】复数代数形式的乘除运算．【分析】利用的运算法则、共轭复数的定义即可得出．【解答】解：复数（2+i）2=3+4i共轭复数为3﹣4i．故选：A．2．设向量=（2x﹣1，3），向量=（1，﹣1），若⊥，则实数x的值为（）A．﹣1 B．1 C．2 D．3【考点】数量积判断两个平面向量的垂直关系．【分析】利用向量垂直的性质求解．【解答】解：∵向量=（2x﹣1，3），向量=（1，﹣1），⊥，∴=（2x﹣1，3）•（1，﹣1）=2x﹣1﹣3=0，解得x=2．故选：C．3．设集合A={﹣1，1}，集合B={x|ax=1，a∈R}，则使得B⊆A的a的所有取值构成的集合是（）A．{0，1}B．{0，﹣1} C．{1，﹣1} D．{﹣1，0，1}【考点】集合的包含关系判断及应用．【分析】利用B⊆A，求出a的取值，注意要分类讨论．【解答】解：∵B⊆A，∴①当B是∅时，可知a=0显然成立；②当B={1}时，可得a=1，符合题意；③当B={﹣1}时，可得a=﹣1，符合题意；故满足条件的a的取值集合为{1，﹣1，0}故选：D．4．执行如图所示的程序框图，输出S的值为（）A．45 B．55 C．66 D．110【考点】程序框图．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算并输出变量S的值，模拟程序的运行，对程序运行过程中各变量的值进行分析，不难得到输出结果．【解答】解：模拟程序的运行，可得：s=0，i=1，i＜10，s=1，i=2，i＜10，s=3，i=3，i＜10，s=6，i=4＜10，s=10，i=5＜10，s=15，i=6＜10，s=21，i=7＜10，s=28，i=8＜10，s=36，i=9＜10，s=45，i=10≤10，s=55，i=11＞10，输出s=5，5，故选：B．5．小孔家有爷爷、奶奶、姥爷、姥姥、爸爸、妈妈，包括他共7人，一天爸爸从果园里摘了7个大小不同的梨，给家里每人一个，小孔拿了最小的一个，爷爷、奶奶、姥爷、姥姥4位老人之一拿最大的一个，则梨子的不同分法共有（）A．96种B．120种C．480种D．720种【考点】排列、组合的实际应用．【分析】小孔的拿法有一种，爷爷、奶奶、姥爷、姥姥4位老人的拿法有4种，其余人的拿法有种，根据乘法原理求得梨子的不同分法．【解答】解：由题意知，小孔拿了最小的一个，爷爷、奶奶、姥爷、姥姥4位老人之一拿最大的一个的拿法有种，其余人的拿法有种，则梨子的不同分法共有480种，故选：C．6．函数的部分图象如图所示，则函数f（x）的解析式为（）A．B．C．D．【考点】由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由题意求出A，T，利用周期公式求出ω，利用当x=时取得最大值2，求出φ，即可得到函数的解析式．【解答】解：由题意可知A=2，T=4（﹣）=π，ω=2，因为：当x=时取得最大值2，所以：2=2sin（2×+φ），所以：2×+φ=2kπ+，k∈Z，解得：φ=2kπ﹣，k∈Z，因为：|φ|＜，所以：可得φ=﹣，可得函数f（x）的解析式：f（x）=2sin（2x﹣）．故选：B．7．设直角坐标平面内与两个定点A（﹣2，0），B（2，0）的距离之差的绝对值等于2的点的轨迹是E，C是轨迹E上一点，直线BC垂直于x轴，则=（）A．﹣9 B．﹣3 C．3 D．9【考点】平面向量数量积的运算．【分析】由条件便可得出轨迹E为双曲线，并可求得方程为，并可求出点C的坐标为（2，3），或（2，﹣3），从而可分别求出向量的坐标，这样即可得出的值．【解答】解：根据题意知，轨迹E是以A，B为焦点的双曲线，方程为，x=2带入方程得：y=±3；∴C点的坐标为（2，3），或（2，﹣3）；（1）若C点坐标为（2，3），则：；∴；（2）若C点坐标为（2，﹣3），则：；∴；综上得，．故选：D．8．利用计算机产生120个随机正整数，其最高位数字（如：34的最高位数字为3，567的最高位数字为5）的频数分布图如图所示，若从这120个正整数中任意取出一个，设其最高位数字为d（d=1，2，…，9）的概率为P，下列选项中，最能反映P与d的关系的是（）A．P=lg（1+）B．P=C．P=D．P=×【考点】频率分布直方图．【分析】利用排除法，即可判断．【解答】解：当d=5时，其概率为P==，对于B，P=，对于C，P=0，对于D，P=，故B，C，D均不符合，故选：A．9．如图，A1，A2为椭圆+=1的长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS，OT围成一个平行四边形OPQR，则|OS|2+|OT|2=（）A．5 B．3+C．9 D．14【考点】椭圆的简单性质．【分析】设Q（x0，y0），则+=1，可得：•=﹣．设直线OS，OT的方程分别为：y=k1x，y=k2x，则=k1，=k2．可得k1k2．直线方程与椭圆方程分别联立可得，；，．即可得出：|OS|2+|OT|2．【解答】解：设Q（x0，y0），则+=1，∴=．设直线OS，OT的方程分别为：y=k1x，y=k2x，则=k1，=k2．∵•===﹣．∴k1k2=﹣．联立，解得=，=．同理可得：=，=．∴|OS|2+|OT|2=+++=+++=+==14．故选：D．10．设a，b是不相等的两个正数，且blna﹣alnb=a﹣b，给出下列结论：①a+b﹣ab＞1；②a+b＞2；③ +＞2．其中所有正确结论的序号是（）A．①② B．①③ C．②③ D．①②③【考点】不等式的基本性质．【分析】①由blna﹣alnb=a﹣b得=，构造函数f（x）=，x＞0，判断a，b的取值范围即可．②由对数平均不等式进行证明，③构造函数，判断函数的单调性，进行证明即可．【解答】解：①由blna﹣alnb=a﹣b，得blna+b=alnb+a，即=，设f（x）=，x＞0，则f′（x）=﹣=，由f′（x）＞0得﹣lnx＞0，得lnx＜0，得0＜x＜1，由f′（x）＜0得﹣lnx＜0，得lnx＞0，得x＞1，即当x=1时，函数f（x）取得极大值，则=，等价为f（a）=f（b），则a，b一个大于1，一个小于1，不妨设0＜a＜1，b＞1．则a+b﹣ab＞1等价为（a﹣1）（1﹣b）＞0，∵0＜a＜1，b＞1．∴（a﹣1）（1﹣b）＞0，则a+b﹣ab＞1成立，故①正确，②由即=，得=，由对数平均不等式得=＞，即lna+lnb＞0，即lnab＞0，则ab＞1，由均值不等式得a+b2，故②正确，③令g（x）=﹣xlnx+x，则g′（x）=﹣lnx，则由g′（x）＞0得﹣lnx＞0，得lnx＜0，得0＜x＜1，此时g（x）为增函数，由g′（x）＜0得﹣lnx＜0，得lnx＞0，得x＞1，此时g（x）为减函数，再令h（x）=g（x）﹣g（2﹣x），0＜x＜1，则h′（x）=g′（x）+g′（2﹣x）=﹣lnx﹣lm（2﹣x）=﹣ln[x（2﹣x）]＞0，则h（x）=g（x）﹣g（2﹣x），在0＜x＜1上为增函数，则h（x）=g（x）﹣g（2﹣x）＜h（1）=0，则g（x）＜g（2﹣x），即g（）＜g（2﹣），∵g（）=﹣ln=+lna==，∴g（）=g（）则g（）=g（）＜g（2﹣），∵g（x）在0＜x＜1上为增函数，∴＞2﹣，即+＞2．故③正确，故选：D二、填空题（每题5分，满分25分，将答案填在答题纸上）11．在（2﹣）6的展开式中，含x3项的系数是64（用数字填写答案）【考点】二项式系数的性质．【分析】根据二项式展开式的通项公式，令展开式中含x项的指数等于3，求出r的值，即可求出展开式中x3项的系数．【解答】解：二项式（2﹣）6展开式的通项公式为=••=（﹣1）r•26﹣r••x3﹣r，T r+1令3﹣r=3，解得r=0；∴展开式中x3项的系数是26×=64．故答案为：64．12．一个几何体的三视图如图所示，则几何体的体积为π．【考点】由三视图求面积、体积．【分析】该几何体是一个半圆柱，即可求出其体积．【解答】解：该几何体是一个半圆柱，如图，其体积为．故答案为：π．13．已知tanα=3，则sinαsin（﹣α）的值是﹣．【考点】同角三角函数基本关系的运用．【分析】利用诱导公式、同角三角函数基本关系式、“弦化切”即可得出．【解答】解：∵tanα=3，则sinαsin（﹣α）=﹣sinαcosα=﹣=﹣=﹣=﹣．故答案为：﹣．14．已知圆的方程为x2+y2﹣6x=0，过点（1，2）的该圆的三条弦的长a1，a2，a3构成等差数列，则数列a1，a2，a3的公差的最大值是2．【考点】等差数列的通项公式．【分析】化圆的一般方程为标准方程，求出圆心坐标和半径，得到最大弦长，再求出过P 且垂直于CP的弦的弦长，即最小弦长，然后利用等差数列的通项公式求得公差得答案．【解答】解：如图，由x2+y2﹣6x=0，得（x﹣3）2+y2=9，∴圆心坐标C（3，0），半径r=3，由圆的性质可知，过点P（1，2）的该圆的弦的最大值为圆的直径，等于6，最小值为过P且垂直于CP的弦的弦长，∵|CP|=，∴|AB|=2，即a1=2，a3=6，∴公差d的最大值为．故答案为：2．15．已知=（1，0），=（1，1），（x，y）=，若0≤λ≤1≤μ≤2时，z=+（m＞0，n＞0）的最大值为2，则m+n的最小值为+．【考点】向量的线性运算性质及几何意义；基本不等式．【分析】化简可得（x，y）=λ（1，0）+μ（1，1），从而可得x=λ+μ，y=μ；从而可得+=1；再化简（m+n）（+）=+1++，从而利用基本不等式求最小值．【解答】解：∵=（1，0），=（1，1），∴（x，y）=λ（1，0）+μ（1，1），∴x=λ+μ，y=μ；z=+=+，∵0≤λ≤1≤μ≤2，z=+（m＞0，n＞0）的最大值为2，∴+=2，即+=1；故（m+n）（+）=+1++≥+2=+；（当且仅当=时，等号成立）．故答案为： +．三、解答题（本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.）16．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足acosB=bcosA．（1）判断△ABC的形状；（2）求sin（2A+）﹣2cos2B的取值范围．【考点】正弦定理；三角函数中的恒等变换应用；余弦定理．【分析】（1）由已知等式结合正弦定理化边为角，再由两角差的余弦求得sin（A﹣B）=0，可得A=B，则△ABC为等腰三角形；（2）把sin（2A+）﹣2cos2B利用两角和的正弦及降幂公式化简，得到关于A的三角函数，再由A的范围求得答案．【解答】解：（1）由acosB=bcosA，结合正弦定理可得，sinAcosB=cosAsinB，即sinAcosB﹣cosAsinB=0，得sin（A﹣B）=0，∵A，B∈（0，π），∴A﹣B∈（﹣π，π），则A﹣B=0，∴A=B，即△ABC为等腰三角形；（2）sin（2A+）﹣2cos2B=sin2Acos+cos2Asin﹣2cos2B=﹣（1+cos2B）=﹣cos2A﹣1==．∵0，∴，则．即sin（2A+）﹣2cos2B的取值范围是．17．设数列{a n}各项为正数，且a2=4a1，a n+1=+2a n（n∈N*）（I）证明：数列{log3（1+a n）}为等比数列；（Ⅱ）令b n=log3（1+a2n﹣1），数列{b n}的前n项和为T n，求使T n＞345成立时n的最小值．【考点】数列的求和；等比数列的通项公式．【分析】（I）由a2=4a1，a n+1=+2a n（n∈N*），可得a2=4a1，a2=，解得a1，a2．由于a n+1+1=+2a n+1=，两边取对数可得：log3（1+a n+1）=2log3（1+a n），即可证明．（II）由（I）可得：log3（1+a n）=2n﹣1，可得b n=log3（1+a2n﹣1）=22n﹣2=4n﹣1，可得数列{b n}的前n项和为T n，代入化简即可得出．【解答】（I）证明：∵a2=4a1，a n+1=+2a n（n∈N*），∴a2=4a1，a2=，解得a1=2，a2=8．∴a n+1+1=+2a n+1=，两边取对数可得：log3（1+a n+1）=2log3（1+a n），∴数列{log3（1+a n）}为等比数列，首项为1，公比为2．（II）解：由（I）可得：log3（1+a n）=2n﹣1，∴b n=log3（1+a2n﹣1）=22n﹣2=4n﹣1，∴数列{b n}的前n项和为T n==．不等式T n＞345，化为＞345，即4n＞1036．解得n＞5．∴使T n＞345成立时n的最小值为6．18．某商场进行有奖促销活动，顾客购物每满500元，可选择返回50元现金或参加一次抽奖，抽奖规则如下：从1个装有6个白球、4个红球的箱子中任摸一球，摸到红球就可获得100元现金奖励，假设顾客抽奖的结果相互独立．（Ⅰ）若顾客选择参加一次抽奖，求他获得100元现金奖励的概率；（Ⅱ）某顾客已购物1500元，作为商场经理，是希望顾客直接选择返回150元现金，还是选择参加3次抽奖？说明理由；（Ⅲ）若顾客参加10次抽奖，则最有可能获得多少现金奖励？【考点】古典概型及其概率计算公式；概率的基本性质．【分析】（Ⅰ）因为从装有10个球的箱子中任摸一球的结果共有种，摸到红球的结果共有种，由此能求出顾客参加一次抽奖获得100元现金奖励的概率．（Ⅱ）设X表示顾客在三次抽奖中中奖的次数，由于顾客每次抽奖的结果是相互独立的，则X﹣B（3，0.4），由此能求出商场经理希望顾客参加抽奖．（Ⅲ）设顾客参加10次抽奖摸中红球的次数为Y．由于顾客每次抽奖的结果是相互独立的，则Y﹣B（10，0.4）．恰好k次中奖的概率为，k=0，1，…，10．由此能求出顾客参加10次抽奖，最有可能获得400元的现金奖励．【解答】解：（Ⅰ）因为从装有10个球的箱子中任摸一球的结果共有种，摸到红球的结果共有种，所以顾客参加一次抽奖获得100元现金奖励的概率是．…（Ⅱ）设X表示顾客在三次抽奖中中奖的次数，由于顾客每次抽奖的结果是相互独立的，则X﹣B（3，0.4），所以E（X）=np=3×0.4=1.2．由于顾客每中奖一次可获得100元现金奖励，因此该顾客在三次抽奖中可获得的奖励金额的均值为1.2×100=120元．由于顾客参加三次抽奖获得现金奖励的均值120元小于直接返现的150元，所以商场经理希望顾客参加抽奖．…（Ⅲ）设顾客参加10次抽奖摸中红球的次数为Y．由于顾客每次抽奖的结果是相互独立的，则Y﹣B（10，0.4）．于是，恰好k次中奖的概率为，k=0，1， (10)从而，k=1，2， (10)当k＜4.4时，P（Y=k﹣1）＜P（Y=k）；当k＞4.4时，P（Y=k﹣1）＞P（Y=k），则P（Y=4）最大．所以，最有可能获得的现金奖励为4×100=400元．于是，顾客参加10次抽奖，最有可能获得400元的现金奖励．…19．如图，在正方形ABCD中，点E，F分别是AB，BC的中点．将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．（1）求证：平面PBD⊥平面BFDE；（2）求二面角P﹣DE﹣F的余弦值．【考点】二面角的平面角及求法；平面与平面垂直的判定．【分析】（1）推导出PD⊥PF，PD⊥PE，则PD⊥平面PEF，由此能证明平面PBD⊥平面BFDE．（2）连结BD、EF，交于点O，以O为原点，OF为x轴，OD为y轴，OP为z轴，建立空间直角坐标系，由此能求出二面角P﹣DE﹣F的余弦值．【解答】证明：（1）由正方形ABCD知，∠DCF=∠DAE=90°，EF∥AC，BD⊥AC，EF⊥BD，∵点E，F分别是AB，BC的中点．将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．∴PD⊥PF，PD⊥PE，∵PE∩PF=P，PE、PF⊆平面PEF．∴PD⊥平面PEF．又∵EF⊂平面PEF，∴PD⊥EF，又BD∩PD=D，∴EF⊥平面PBD，又EF⊂平面BFDE，∴平面PBD⊥平面BFDE．解：（2）连结BD、EF，交于点O，以O为原点，OF为x轴，OD为y轴，OP为z轴，建立空间直角坐标系，设在正方形ABCD的边长为2，则DO=，=，PE=PF=1，PO==，∴P（0，0，），D（0，，0），E（﹣，0，0），F（，0，0），=（﹣，﹣，0），=（0，﹣，），=（，﹣，0），设平面PDE的法向量=（x，y，z），则，取y=1，则=（﹣3，，3），平面DEF的法向量=（0，0，1），设二面角P﹣DE﹣F的平面角为θ，则cosθ===．∴二面角P﹣DE﹣F的余弦值为．20．已知直线l的方程为y=x+2，点P是抛物线y2=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y2=4x 交于点B．（Ⅰ）求点P的坐标；（Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．【考点】直线与抛物线的位置关系．【分析】（Ⅰ）利用点到直线的距离公式，求出最小值，然后求点P的坐标；（Ⅱ）设点A的坐标为，显然y1≠2．通过当y1=﹣2时，求出直线AP的方程为x=1；当y1≠﹣2时，求出直线AP的方程，然后求出Q的坐标，求出B点的坐标，解出直线AB的斜率，推出AB的方程，判断直线AB恒过定点推出结果．【解答】解：（Ⅰ）设点P的坐标为（x0，y0），则，所以，点P到直线l的距离．当且仅当y0=2时等号成立，此时P点坐标为（1，2）．…（Ⅱ）设点A的坐标为，显然y1≠2．当y1=﹣2时，A点坐标为（1，﹣2），直线AP的方程为x=1；当y1≠﹣2时，直线AP的方程为，化简得4x﹣（y1+2）y+2y1=0；综上，直线AP的方程为4x﹣（y1+2）y+2y1=0．与直线l的方程y=x+2联立，可得点Q的纵坐标为．因为，BQ∥x轴，所以B点的纵坐标为．因此，B点的坐标为．当，即时，直线AB的斜率．所以直线AB的方程为，整理得．当x=2，y=2时，上式对任意y1恒成立，此时，直线AB恒过定点（2，2），当时，直线AB的方程为x=2，仍过定点（2，2），故符合题意的直线AB恒过定点（2，2）．…21．设a，b∈R，函数，g（x）=e x（e为自然对数的底数），且函数f（x）的图象与函数g（x）的图象在x=0处有公共的切线．（Ⅰ）求b的值；（Ⅱ）讨论函数f（x）的单调性；（Ⅲ）若g（x）＞f（x）在区间（﹣∞，0）内恒成立，求a的取值范围．【考点】利用导数研究函数的单调性；导数在最大值、最小值问题中的应用．【分析】（Ⅰ）求出两个函数的导数，利用函数f（x）的图象与函数g（x）的图象在x=0处有公共的切线．列出方程即可求解b．（Ⅱ）求出导函数f'（x）=，通过﹣1≤a≤1时，当a2＞1时，分别判断导函数的符号，推出函数的单调区间．（Ⅲ）令h（x）=g'（x）﹣f'（x）=e x﹣x2﹣2ax﹣1，可得h（0）0．求出h'（x）=e x﹣2x﹣2a，令u（x）=h'（x）=e x﹣2x﹣2a，求出导数u'（x）=e x﹣2．当x≤0时，u'（x）＜0，从而h'（x）单调递减，求出．考虑的情况，的情况，分别通过函数的单调性以及函数的最值，推出a的范围即可．【解答】（Ⅰ）f'（x）=x2+2ax+b，g'（x）=e x，由f'（0）=b=g'（0）=1，得b=1．…（Ⅱ）f'（x）=x2+2ax+1=（x+a）2+1﹣a2，当a2≤1时，即﹣1≤a≤1时，f'（x）≥0，从而函数f（x）在定义域内单调递增，当a2＞1时，，此时若，f'（x）＞0，则函数f（x）单调递增；若，f'（x）＜0，则函数f（x）单调递减；若时，f'（x）＞0，则函数f（x）单调递增．…（Ⅲ）令h（x）=g'（x）﹣f'（x）=e x﹣x2﹣2ax﹣1，则h（0）=e0﹣1=0．h'（x）=e x﹣2x ﹣2a，令u（x）=h'（x）=e x﹣2x﹣2a，则u'（x）=e x﹣2．当x≤0时，u'（x）＜0，从而h'（x）单调递减，令u（0）=h'（0）=1﹣2a=0，得．先考虑的情况，此时，h'（0）=u（0）≥0；又当x∈（﹣∞，0）时，h'（x）单调递减，所以h'（x）＞0；故当x∈（﹣∞，0）时，h（x）单调递增；又因为h（0）=0，故当x＜0时，h（x）＜0，从而函数g（x）﹣f（x）在区间（﹣∞，0）内单调递减；又因为g（0）﹣f（0）=0，所以g（x）＞f（x）在区间（﹣∞，0）恒成立．接下来考虑的情况，此时，h'（0）＜0，令x=﹣a，则h'（﹣a）=e﹣a＞0．由零点存在定理，存在x0∈（﹣a，0）使得h'（x0）=0，当x∈（x0，0）时，由h'（x）单调递减可知h'（x）＜0，所以h（x）单调递减，又因为h（0）=0，故当x∈（x0，0）时h（x）＞0．从而函数g（x）﹣f（x）在区间（x0，0）单调递增；又因为g（0）﹣f（0）=0，所以当x∈（x0，0），g（x）＜f（x）．综上所述，若g（x）＞f（x）在区间（﹣∞，0）恒成立，则a的取值范围是．…2017年1月12日。

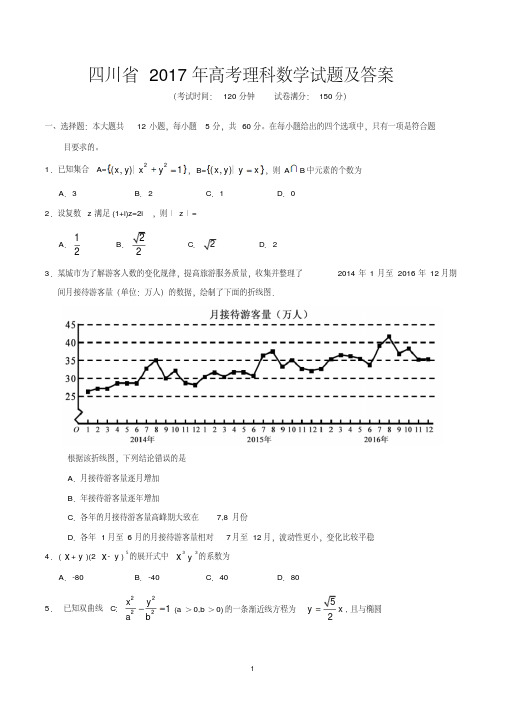
四川省2017年高考理科数学试题及答案（考试时间:120分钟 试卷满分:150分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A={}22(,)1x y x y +=│，B={}(,)x y y x =│，则A B 中元素的个数为A ．3B ．2C ．1D ．02．设复数z 满足（1+i)z=2i ，则∣z ∣= A ．12B ．22C ．2D ．23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图,下列结论错误的是 A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 4．（x +y ）（2x -y ）5的展开式中x 3y 3的系数为A ．-80B ．-40C ．40D ．805． 已知双曲线C ：22221x y a b -= (a ＞0，b ＞0）的一条渐近线方程为52y x =，且与椭圆221123x y += 有公共焦点,则C 的方程为 A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -= 6．设函数f(x)=cos （x+3π)，则下列结论错误的是 A ．f （x ）的一个周期为−2πB ．y=f(x ）的图像关于直线x=83π对称 C ．f(x+π）的一个零点为x=6πD ．f(x ）在（2π，π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为 A ．5 B ．4C ．3D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．3π4C ．π2D ．π49．等差数列{}n a 的首项为1,公差不为0．若a 2,a 3，a 6成等比数列，则{}n a 前6项的和为 A ．—24B ．-3C ．3D ．810．已知椭圆C:22221x y a b+=,(a 〉b 〉0）的左、右顶点分别为A 1,A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A ．63B ．33C ．23D ．1311．已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a=A ．12-B ．13C ．12D ．112．在矩形ABCD 中,AB=1，AD=2,动点P 在以点C 为圆心且与BD 相切的圆上．若AP =λ AB +μAD ，则λ+μ的最大值为A．3 B．CD．2二、填空题：本题共4小题，每小题5分，共20分.13．若x，y满足约束条件y020xx yy-≥⎧⎪+-≤⎨⎪≥⎩，则z34x y=-的最小值为__________．14．设等比数列{}n a满足a1 + a2 = –1, a1– a3 = –3，则a4 = ___________．15．设函数10()20xx xf xx+≤⎧=⎨>⎩，，，，则满足1()()12f x f x+->的x的取值范围是_________.16．a，b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：①当直线AB与a成60°角时,AB与b成30°角；②当直线AB与a成60°角时，AB与b成60°角；③直线AB与a所称角的最小值为45°;④直线AB与a所称角的最小值为60°；其中正确的是________。

第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.设i 为虚数单位，复数z 满足21ii z=-，则复数z 等于（ ） A ．1i -- B ．1i - C ．1i + D ．1i -+ 【答案】D 【解析】试题分析： 由题意可知, 211iz i i==-+-. 考点： 复数运算.2. 设集合2{|20}M x x x =-≥，{|N x y ==，则MN 等于（ ）A ．(1,0]-B ．[1,0]-C ．[0,1)D ．[0,1] 【答案】C考点：集合的交集运算.3. 已知(,0)2x π∈-，4tan 3x =-，则sin()x π+等于（ ） A ．35 B ．35- C ．45- D ．45【答案】D 【解析】试题分析：因为(,0)2x π∈-，4tan 3x =-，所以4sin 5x =-，4sin()sin 5x x π+=-=． 考点：三角函数值.4. 从某项综合能力测试中抽取100人的成绩，统计如下，则这100个成绩的平均数为（ ）A ．3B ．2.5C ．3.5D ．2.75 【答案】A考点：平均数.5. 已知双曲线2222:1(0,0)x y C a b a b -=>>的渐近线方程为34y x =±，且其右焦点为（5,0），则双曲线C的方程为（ ）A ．221916x y -=B ．221169x y -=C ．22134x y -=D ．22143x y -=【答案】B 【解析】试题分析：由题意得34b a =，22225c a b =+=，所以4a =，3b =，所求双曲线方程为221169x y -=．考点：双曲线的性质.6. 将函数()cos 22x x f x =-的图象向右平移23π个单位长度得到函数()y g x =的图象，则函数()y g x =的一个单调递减区间是（ ）A ．(,)42ππ-B ．(,)2ππC ．(,)24ππ--D ．3(,2)2ππ 【答案】C 【解析】试题分析： 因为()2sin()26x f x π=-，所以2()()2sin()2cos 32632x xg x f x πππ=-=--=-，则()g x 在(,)24ππ--上递减．考点：三角函数的性质.7. 设e 是自然对数的底，0a >且1a ≠，0b >且1b ≠，则“log 2log a b e >”是“01a b <<<”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】B考点：充分必要条件.【方法点睛】充分不必要条件、必要不充分条件、既不充分也不必要条件的判断的一般方法： ①充分不必要条件：如果p q ⇒，且p q ⇐/，则说p 是q 的充分不必要条件； ②必要不充分条件：如果p q ⇒/，且p q ⇐，则说p 是q 的必要不充分条件； ③既不充分也不必要条件：如果p q ⇒/，且p q ⇐/，则说p 是q 的既不充分也不必要条件.8. 某几何体的三视图如图所示，则该几何体的体积是（ ）A ．423π+B ．443π+ C ．44π+ D ．24π+ 【答案】A 【解析】试题分析： 该几何体可以看作是14个圆柱体和一个三棱锥组合而成，故体积()2111422(22)224323V ππ=⨯⨯+⨯⨯⨯=+． 考点：三视图.9. 右边程序框图的算法思路来源于我国古代数学名著《数书九章》中的“秦九韶算法”求多项式的值.执行程序框图，若输入01a =，11a =，20a =，31a =-，则输出u 的值为（ ）A ．2B ．1C ．0D ．-1 【答案】B考点：程序框图.10. 如图，在三棱柱111ABC A B C -中，底面为正三角形，侧棱垂直底面，4AB =,16AA =.若E ，F 分别是棱1BB ，1CC 上的点，且1BE B E =，1113C F CC =，则异面直线1A E 与AF 所成角的余弦值为（ ）A B C D 【答案】D【解析】试题分析：以BC 的中点O为坐标原点建立空间直角坐标系如图所示，则A，1A ，(0,2,3)E ，(0,2,4)F -，1(2,3)A E =--，(2,4)AF =--，设1A E ，AF 所成的角为θ，则11||cos ||||5A E AF A E AF θ⋅===⋅⨯．考点： 线面角.11. 如图，椭圆的中心在坐标原点，焦点在x 轴上，1A ，2A ，1B ，2B 为椭圆的顶点，2F 为右焦点，延长12B F 与22A B 交于点P ，若12B PB ∠为钝角，则该椭圆的离心率的取值范围是（）A ．B ．C． D ． 【答案】C考点：椭圆的性质.【思路点睛】根据12B PB ∠为22B A 与21F B 的夹角，并分别表示出22B A 与21F B ，由∠B 1PB 2为钝角，222210B A F B ac b =-+>，利用椭圆的性质，可得到210e e +-<，即可解得离心率的取值范围．12. 设函数()f x 在R 上存在导函数'()f x ，对于任意的实数x ，都有2()4()f x x f x =--，当(,0)x ∈-∞时，1'()42f x x +<.若(1)()42f m f m m +≤-++，则实数m 的取值范围是（ ）A ．1[,)2-+∞ B ．3[,)2-+∞ C ．[1,)-+∞ D ．[2,)-+∞ 【答案】A考点：导数在函数单调性中的应用.【思路点睛】因为22()2()20f x x f x x -+--=，设2()()2g x f x x =-，则()()0g x g x +-=，可得()g x 为奇函数，又1'()'()42g x f x x =-<-，得()g x 在(,0)-∞上是减函数，从而在R 上是减函数，在根据函数的奇偶性和单调性可得(1)()g m g m +≤-，由此即可求出结果.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 设变量x ，y 满足约束条件20,320,4520.y x y x y -≥⎧⎪-+≤⎨⎪-+≥⎩，则目标函数2z x y =+的最大值为__________.【答案】8 【解析】试题分析：根据约束条件画出可行域，当过点(4,2)时，2z x y =+取最大值为8. 考点：简单的线性规划. 在几区14. 在矩形ABCD 中，30CAB ∠=，||AC AD AC =，则AC AB =____________. 【答案】12考点： 平面向量的数量积.15. 61(21)()x x x-+的展开式中3x 的系数为______________. 【答案】30 【解析】试题分析：因为61()x x +的通项公式为6216r rr T C x -++=，所以61(21)()x x x-+的展开式中含x 的奇数次方的通项为5262r r C x -+，令523r -+=，解得4r =.从而所求的系数为46230C =.考点：二项式定理.【思路点睛】本题考查二项式定理，二项展开式的通项公式，求展开式中某项的系数，根据61(21)()x x x-+的展开式的含3x 的项由两类构成，然后求出各类的含4x 的项，再将各个项加起来，即可得到所求的项的系数．16. 在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足22cos 2A A =，sin()4cos sin B C B C -=，则bc=____________.【答案】1 【解析】试题分析：因为22cos 2A A =，所以1cos A A +=，化简得sin()3A π-=.所以23A π=．又因为sin()4cos sin B C B C -=，所以sin cos cos sin 6cos sin B C B C B C +=，所以sin 6cos sin A B C =，即22262c a b a c ca+-=⨯，整理得2222330a c b +-=.又2222212()2a b c bc b c bc =+-⋅-=++，所以22250b bc c --=，两边除以2c 得22()50b bc c--=，解得1bc=+. 考点：余弦定理.【思路点睛】因为22cos 2A A =，化简得sin()3A π-=所以23A π=．又因为sin()4cos sin B C B C -=，所以sin 6cos sin A B C =，由正弦定理和余弦定理整理得2222330a c b +-=.，化简可的22250b bc c --=，两边除以2c 得22()50b b c c --=，即可求得bc.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. （本小题满分12分）设数列{}n a 是公差大于0的等差数列，n S 为数列{}n a 的前n 项和.已知39S =，且12a ，31a -，41a +构成等比数列.（1）求数列{}n a 的通项公式； （2）若数列{}n b 满足1*2()n nna n Nb -=∈，设n T 是数列{}n b 的前n 项和，证明6n T <. 【答案】（1）21n a n =-；（2）详见解析考点：1.等差数列；2.错位相减.【方法点睛】针对数列{}n n a b ⋅（其中数列{}{},n n a b 分别是等差数列和等比数列（公比1q ≠）），一般采用错位相减法求和，错位相减的一般步骤是:1.112233...n n n S a b a b a b a b =++++…①；2.等式112233...n n n S a b a b a b a b =++++两边同时乘以等比数列{}n b 的公比，得到112233...n n n qS a b q a b q a b q a b q =++++…②；3.最后①-②，化简即可求出结果.18. （本小题满分12分）中国乒乓球队备战里约奥运会热身赛暨选拔赛于2016年7月14日在山东威海开赛.种子选手M 与1B ，2B ，3B 三位非种子选手分别进行一场对抗赛，按以往多次比赛的统计，M 获胜的概率分别为34，23，12，且各场比赛互不影响.（1）若M 至少获胜两场的概率大于710，则M 入选征战里约奥运会的最终大名单，否则不予入选，问M 是否会入选最终的大名单？（2）求M 获胜场数X 的分布列和数学期望. 【答案】（1）M 会入选最终的大名单；（2）2312（2）M 获胜场数X 的可能取值为0,1,2,3，则3211(0)()(1)(1)(1)43224P X P ABC ===-⨯-⨯-=，……………………………………………………7分 3213213216(1)()()()(1)(1)(1)(1)(1)(1)43243243224P X P ABC P ABC P ABC ==++=⨯-⨯-+-⨯-⨯+-⨯⨯-=……………………………………………………………………………………………………………………8分32132132111(2)()()()(1)(1)(1)43243243224P X P ABC P ABC P ABC ==++=⨯⨯-+⨯-⨯+-⨯⨯=…9分 3216(3)()43224P X P ABC ===⨯⨯=………………………………………………………………………10分 所以M 获胜场数X 的分布列为：……………………………………………………………………………………………………………………11分数学期望为1611623()01232424242412E X =⨯+⨯+⨯+⨯=.………………………………………………12分 考点：1.对立事件的概率；2.离散型分布列和期望.19. （本小题满分12分）如图，在三棱锥A BCD -中，AD ⊥平面BCD ，CB CD =，AD DB =，P ，Q 分别在线段AB ，AC 上，3AP PB =，2AQ QC =，M 是BD 的中点.（1）证明：//DQ 平面CPM ；（2）若二面角C AB D --的大小为3π，求tan BDC ∠.【答案】（1）详见解析；（2由（1）知//DE PM ，而DE AB ⊥，故PM AB ⊥.所以CPM ∠是二面角C AB D --的平面角， 则3CPM π∠=.…………………………………………………………………………………………………9分设PM a =，则CM =，又易知在Rt ABD ∆中，4B π∠=，可知DM BM ==，在Rt CMD ∆中，tan MC MDC MD ∠===.………………………………………………………12分 考点：1.线面线面平行的判断；2.二面角.【一题多解】以M 为坐标原点，MC ，MD ，ME 所在的直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系.设MC a =，MD b =，则(,0,0)C a ，(0,,0)B b -，(0,,2)A b b ，………………………………………7分 则(,,0)BC a b =，(0,2,2)BA b b =，设1(,,)n x y z =是平面ABC 的一个法向量，20. （本小题满分12分）已知抛物线2:2(0)E y px p =>，直线3x my =+与E 交于A ，B 两点，且6OA OB =，其中O 为坐标原点.（1）求抛物线E 的方程；（2）已知点C 的坐标为（-3,0），记直线CA 、CB 的斜率分别为1k ，2k ，证明：22212112m k k +-为定值. 【答案】（1）2y x =；（2）详见解析【解析】试题分析：设11(,)A x y ，22(,)B x y ，联立方程组223y px x my ⎧=⎨=+⎩，消元得2260y pmy p --=，所以122y y pm +=，126y y p =-.又2121212122()4y y OA OB x x y y y y p ⋅=+=+，所以12p =，从而求出结果.（2）（2）因为1111136y y k x my ==++，2222236y y k x my ==++， 所以1116m k y =+，2216m k y =+，……………………………………………………………………………6分 因此222222121211662()()2m m m m k k y y +-=+++- 222212*********()36()2m m m y y y y =++++-………………………………………………………………8分 222121212221212()2212362y y y y y y m m m y y y y ++-=++- 又122y y pm m +==，1263y y p =-=-，…………………………………………………………………9分所以2222221211622123622439m m m m m m k k -++-==+⨯+⨯-=.……………………………………11分 即22212112m k k +-为定值.……………………………………………………………………………………12分 考点：1.抛物线方程；2.直线与抛物线的位置关系.21. （本小题满分12分）已知函数1()()ln (0)a x f x a x a x a a=+-->. （1）求函数()f x 的单调区间和极值；（2）证明：当1[,2]2a ∈时，函数()f x 没有零点（提示：ln 20.69≈）【答案】（1）详见解析；（2）详见解析试题解析：解：（1）因为2211()()ln [(1)ln ]a x a f x a x x a x x a a a x=+--=+--， 所以22(1)()'()x x a f x ax +-=.…………………………………………………………………………………2分 因为0x >，所以当2(0,)x a ∈时，'()0f x <，当时2(,)x a ∈+∞，'()0f x >.所以函数()f x 的单调递增区间为2(,)a +∞，单调减区间为2(0,)a .………………………………………4分 当2x a =时，()f x 取得极小值22221()[1(1)ln ]f a a a a a=+--.…………………………………………5分 （2）由（1）可知：当2x a =时，()f x 取得极小值，亦即最小值.22221()[1(1)ln ]f a a a a a =+--，又因为122a ≤≤，所以2144a ≤≤． 设1()1(1)ln (4)4g x x x x x =+--≤≤，则1'()ln g x x x=-，……………………………………………7分 因为'()g x 在1[,4]4上单调递减，且'(1)0g >，'(2)0g <，所以'()g x 有唯一的零点(1,2)m ∈，使得()g x 在1[,)4m 上单调递增，在(,4]m 上单调递减，…………9分 又由于156ln 2()044g -=>，(4)56ln 20g =->，……………………………………………………10分 所以()0g x >恒成立.从而22221()[1(1)ln ]0f a a a a a=+-->恒成立，则()0f x >恒成立. 所以当1[,2]2a ∈时，函数()f x 没有零点.…………………………………………………………………12分 考点：1.导数在求函数极值中的应用； 2.函数的零点. 请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22. （本小题满分10分）选修4-1：几何证明选讲如图，点C 是圆O 直径BE 的延长线上一点，AC 是圆O 的切线，A 为切点，ACB ∠的平分线CD 与AB 相交于点D ，与AE 相交于点F .（1）求EFC ∠的度数；（2）若AB AC =，证明：2AB AE BC =⋅.【答案】（1）45EFC ∠=；（2）详见解析考点： 与圆有关的比例线段．23. （本小题满分10分）选修4-4：坐标系与参数方程在平面直角坐标系xOy中，已知曲线:sin x a C y a⎧=⎪⎨=⎪⎩（a 为参数），直线:60l x y --=. （1）在曲线C 上求一点P ，使点P 到直线l 的距离最大，并求出此最大值；（2）过点(1,0)M -且与直线l 平行的直线1l 交C 于A ，B 两点，求点M 到A ，B 两点的距离之积.【答案】（1）；（2）1【解析】试题分析：（1）化极坐标方程为 普通方程，设出P 的坐标，利用点到直线的距离公式求出距离，利用三角函数的最值求出此最大值；（2）求出椭圆的参数方程，利用此时的几何意义，求解点M 到A B ，两点的距离之积．试题解析：解：（1）设点,sin )P a a ，则点P 到直线l 的距离为d == ∴当sin()13a π-=-时，31(,)22P -，此时max d =……………………………………………………5分 （2）曲线C 化为普通方程为：2213x y +=，即2233x y +=，直线1l的参数方程为1,.x y ⎧=-+⎪⎪⎨⎪=⎪⎩（t 为参数），代入2233x y +=化简得：2220t --=，得121t t =-，∴12||||||1MA MB t t ⋅==.……………………………………………………………………………………10分 考点：1.简单曲线的极坐标方程；2.参数方程化成普通方程．24. （本小题满分10分）选修4-5：不等式选讲 设函数()|||2|(0)f x x a x a a =-+-<.（1）证明：1()()6f x f x +-≥；（2）若不等式1()2f x <的解集为非空集，求a 的取值范围. 【答案】（1）详见解析；（2）（-1,0）考点：1.绝对值不等式；2.基本不等式.：。

2020届四川省高三上学期巴蜀黄金大联考数学（理）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合{}{}2|4120,|23A x x x B x x =--<=>,则A B =（ ）A ．3,62⎛⎫⎪⎝⎭ B ． 3,22⎛⎫⎪⎝⎭C ．()1,6D ．()1,2 2.若复数()421aiz a R i-=∈-的实部为1，则z 的虚部为 （ ） A ．1 B ．3 C ．1- D ．3- 3. 已知向量()()2,,1,2a m b ==-，若()222a a b b m -=+，则实数m = （ ）A ．12 B ．52 C ．544. 巳知47972coscos sin sin cos cos 51551523x x πππππ⎛⎫-=++ ⎪⎝⎭，则sin 2x =（ ） A ．13 B ． 13- C. 112 D ．112- 5. 执行如图所示的程序框图，输出S 的值为（ ）A ．14B ．20 C. 30 D ．556. 若实数,x y 满足条件1022010x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩，则543z x y =-+的最大值为 （ ）A ．158-B ．54- C.12- D ．1- 7. “()22143m x dx ≤-⎰”是“函数()122x x m f x +=+的值不小于4” 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．即不充分也不必要条件8. 甲、乙、丙三位同学将独立参加英语听力测试，根据平时训练的经验，甲、乙、丙三人能达标的概率分别为23,,35P ，若三人中有人达标但没有全部达标的概率为23，则P =（ ） A ．23 B ．34 C.45 D ．569. 已知函数()()12cos cos 3f x x x ϕ=++是偶函数，其中0,2πϕ⎛⎫∈ ⎪⎝⎭，则下列关于函数()()cos 2g x x ϕ=-的正确描述是 （ ）A ．()g x 在区间上,123ππ⎡⎤-⎢⎥⎣⎦的最小值为1- B ．()g x 的图象可由函数()f x 的图象先向上平移2个单位，再向右平移3π个单位得到C. ()g x 的图象可由函数()f x 的图象向左平移3π个单位得到D ．()g x 的图象可由函数()f x 的图象向右平移3π个单位得到10. 已知函数()2,011,1x f x x -<<⎧=⎨≥⎩，则不等式()2134log log 41log 15x x f x ⎛⎫--+≤ ⎪⎝⎭的解集为（ ）A ．1,13⎛⎫ ⎪⎝⎭B ．[]1,4 C. 1,43⎛⎫ ⎪⎝⎭D ．[)1,+∞11. 已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为(),0,,F c M N -在双曲线C 上，O 是坐标原点，若四边形OFMN 为平行四边形，且四边形OFMN，则双曲线C 的离心率为（ ） AB ．2C.．12. 已知函数()()263,x e exf x x xg x ex+=---=，实数,m n 满足0m n <<，若[]()12,,0,x m n x ∀∈∃∈+∞，使得()()12f x g x =成立，则n m -的最大值为 （ ）A ．4B ．．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 51x ⎛⎫- ⎪⎝⎭的展开式中的常数项为 __________.14. 若抛物线()220y px p =>上的点()00,22p x x ⎛⎫>⎪⎝⎭到其焦点的距离为52，则p = __________. 15. 已知等差数列{}n a 的前n 项和为n S ，且3634a a =+，若510S <，则2a 的取值范围是 _________. 16. 在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ，22sin cos sin cos 4sin ,cos c A A a C C B B D +==是AC 上一点，且23BCD S ∆=，则AD AC = _________.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）已知数列{}n a 的前n 项和为n S ，且()163n n S a n N +*=+∈. （1）求a 的值及数列{}n a 的通项公式；（2）设 ()()2311log n nn b an a a +=-，求1n b ⎧⎫⎨⎬⎩⎭的前n 项和为n T .18.（本小题满分12分）在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ，且232cos cos a c bA B-=.（1） 若b B =,求a ；（2）若a ABC =∆求b c +. 19.（本小题满分12分）为推行“新课堂”教学法，某化学老师分別用原传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班进行教学实验，为了解教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图，记成绩不低于70分者为“成绩优良”.（1）由以上统计数据填写下面22⨯列联表，并判断能否在犯错误的摡率不超过0.025的前提下认为“ 成绩优良与教学方式有关” ？ 附:()()()()()22n ad bc K a b a d a c b d -=++++，其中n a b c d =+++独立性检验临界表（2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法来抽取8人进行考核，在这8人中，记成绩不优良的乙班人数为X ，求X 的分布列及数学期望.20.（本小题满分12分）已知右焦点为(),0F c 的椭圆()2222:10x y M a b a b +=>>过点31,2⎛⎫⎪⎝⎭，且椭圆M关于直线x c =对称的图形过坐标原点. （1）求椭圆M 的方程；（2）过点()4,0且不垂直于y 轴的直线与椭圆M 交于,P Q 两点，点Q 关于x 轴的对称点为E ，证明: 直线PE 与x 轴的交点为F .21.（本小题满分12分）已知函数()()()322ln f x a x a x a R =--+-∈. （1）若函数()y f x =在区间()1,3上单调，求a 的取值范围 ； （2）若函数()()g x f x x =-在10,2⎛⎫⎪⎝⎭上无零点， 求a 的最小值.请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-4：坐标系与参数方程已知极点与直角坐标系的原点重合 ，极轴与x 轴的正半轴重合，圆C 的极坐标是2sin a ρθ=，直线l 的参数方程是35(45x t a t y t ⎧=-+⎪⎪⎨⎪=⎪⎩为参数）.（1）若2,a M =为直线l 与x 轴的交点，N 是圆C 上一动点，求MN 的最大值； （2）若直线l 被圆C截得的弦长为求a 的值 . 23.（本小题满分10分）选修4-5：不等式选讲 设函数()1f x x =+. （1）解不等式()2f x x <； （2） 若()28f x x a+->对任意x R ∈恒成立，求实数a 的取值范围.2020届四川省高三上学期巴蜀黄金大联考数学（理）试题参考答案一、选择题（每小题5分，共60分）1-5. CBDAC 6-10.CABCC 11-12.DA 二、填空题（每小题5分，共20分）13. 20- 14. 1 15. (),2-∞ 16. 59三、解答题17.解：（1）163,n n S a +=+∴当1n =时，11669S a a ==+；当2n ≥时，()16623n n n n a S S -=-= ，即{}13,n n n a a -=∴是等比数列，11a ∴=，则96a +=，得3,a =-∴数列{}n a 的通项公式为()13n n a n N -*=∈.()2sin cos 3sin cos 2sin cos ,2sin cos sin cos 2sin 3sin cos A B C A B A A B B A C C A =-∴+== ，2sin 0,cos 3C A ≠∴=，则sin 5sin ,A b B ==∴由正弦定理得：5sin sin 3b a A B ==.（2）ABC ∆1sin 2bc A ∴=，得()2224103,6,6,633bc a b c bc b c bc ==∴+-=∴+-=，即()216,0,0,4b c b c b c +=>>∴+=.19.解：（1）根据22⨯列联表中的数据，得2K 的观测值为()240941611 5.227 5.024,25152020k ⨯-⨯=≈>∴⨯⨯⨯能在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”. （2）由表可知在8人中成绩不优良的人数为158340⨯=，则X 的可能取值为0,1,2,3. ()()()()32112311114114433331515151533446640;1;2;39191455455C C C C C C P X P X P X P X C C C C ============. X ∴的分布列为：()01239191455455455E X ∴=⨯+⨯+⨯+⨯=. 20.解：（1）椭圆M 过点223191,,124ab ⎛⎫∴+= ⎪⎝⎭， ① 椭圆M 关于直线x c =对称的图形过坐标原点，2222232,,4a c abc b a ∴==+∴=，② 由①②得224,3,a b ==∴椭圆M 的方程为22143x y +=. （2）证明：易知直线PQ 的斜率必存在，设直线PQ 的的方程为()()40y k x k =-≠，代人22143x y +=得()2222343264120k xk x k +-+-=，由()()()2222324364120k k k ∆=--+->得，11,22k ⎛⎫∈- ⎪⎝⎭，设()()()112222,,,,,P x y Q x y E x y -，则22121222326412,3434k k x x x x k k-+==++，则直线PE 的方程为()1212112y y y y x x x x +-=--，令0y =得：()()()122112122111121212448x k x x k x x x x y x y x y x y y y y k x x -+--+=-+==+++- ()222212122122641232242434341328834k k x x x x k k k x x k ---+++===+--+， ∴直线PE 过定点()1,0，又M 的右焦点为()1,0，∴直线PE 与x 轴的交点为F .21.解：（1）()()322'3a x f x a x x--=--=,当3a ≥时，()'0f x <，即函数()f x 在区间()1,3上单调递减，当3a <时，令()'0f x =，得23x a =-，若函数()y f x =在区间()1,3上单调递增，则213a≤-或233a ≥-，解得1a ≤或733a ≤<；综上，a 的取值范围是(]7,1,3⎡⎫-∞+∞⎪⎢⎣⎭. （2）因为当0x →时，()g x →+∞，所以()()()212ln 0g x a x x =---<在区间10,2⎛⎫⎪⎝⎭上恒成立不可能，故要使函数()g x 在10,2⎛⎫ ⎪⎝⎭上无零点，只要对任意的()10,,02x g x ⎛⎫∈> ⎪⎝⎭上恒成立，即对12ln 0,,221x x a x ⎛⎫∈>- ⎪-⎝⎭恒成立，令()2ln 12,0,12x l x x x ⎛⎫=-∈ ⎪-⎝⎭，则()()()()222212ln 2ln 2'11x x x x x l x x x --+-=-=--，再令()212ln 2,0,2m x x x x ⎛⎫=+-∈ ⎪⎝⎭，则 ()()222122'0x m x x x x --=-+=<，故()m x 在10,2⎛⎫ ⎪⎝⎭上为减函数，于是()122ln 202m x m ⎛⎫>=-> ⎪⎝⎭，从而，()'0l x >，()l x 在10,2⎛⎫ ⎪⎝⎭上为增函数，所以()124ln 22l x l ⎛⎫<=- ⎪⎝⎭，故要使2ln 21x a x >--上恒成立，只要[)24ln 2,a ∈-+∞，综上，()g x 在10,2⎛⎫⎪⎝⎭上无零点，则a 的最小值为24ln 2-. 22.解：（1）由24sin ρρθ=得圆C 可化为2240x y y +-=， 将直线l 的参数方程化为直角坐标方程，得()423y x =--，令0y =，得2x =，即点M 的坐标为()2,0.又圆C 的圆心坐标为()0,2，半径2r =，则MC=，所以MN 的最大值为2MC r +=+.（2）因为圆()222:C x y a a +-=，直线:4340l x y a +-=，所以圆心C 到直线l的距离为34,55a a ad -==∴=52a =±. 23.解：（1） 由()2f x x <得12x x +<，则212x x x -<+<，即1212x xx x +<⎧⎨+>-⎩，解得1,x >∴不等式()2f x x <的解集为()1,+∞.（2）()111f x x a x x a x x a a +-=++-≥+-+=+,又()3282f x x a +->=对任意x R ∈恒成立，即()3f x x a +->对任意x R ∈恒成立，13a ∴+>，解得4a <-或2a >，∴实数a 的取值范围是()(),42,-∞-+∞.、。

四川省2017年高考理科数学试题及答案（考试时间：120分钟 试卷满分：150分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A={}22(,)1x y x y +=│，B={}(,)x y y x =│，则A B 中元素的个数为A ．3B ．2C ．1D ．02．设复数z 满足(1+i)z=2i ，则∣z ∣=A ．12B ．2C D ．23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是 A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 4．(x +y )(2x -y )5的展开式中x 3y 3的系数为A ．-80B ．-40C ．40D ．805． 已知双曲线C ：22221x y a b-= (a ＞0,b ＞0)的一条渐近线方程为2y x =,且与椭圆221123x y += 有公共焦点，则C 的方程为 A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -= 6．设函数f(x)=cos(x+3π)，则下列结论错误的是 A ．f(x)的一个周期为−2πB ．y=f(x)的图像关于直线x=83π对称 C ．f(x+π)的一个零点为x=6πD ．f(x)在(2π,π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为 A ．5 B ．4C ．3D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．3π4C ．π2D ．π49．等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为A ．-24B ．-3C ．3D ．810．已知椭圆C ：22221x y a b+=，（a>b>0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A ．3B ．3C ．3D ．1311．已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a=A．12-B．13C．12D．112．在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若AP=λAB+μAD，则λ+μ的最大值为A．3 B．CD．2二、填空题：本题共4小题，每小题5分，共20分。

数学（理科）考试时间：2016年12月6日下午15：00~17：00考生注意：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。

2．请将各题答案填在试卷后面的答题卡上。

3．本试卷主要考试内容：必修1、3、4、5，选修1—1、1—2（立体几何不考大纲）。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分，在没小题给出的四个选项中，只有一项是符合题目要求的1. 已知集合}3log 2|{}0124|{32＞，＜x x B x x x A =--=，则B A 等于（ ） A.)6,23( B.)2,23( C.(1，6) D,(1，2)2. 若复数)(124R a iaiz ∈--=的实部为1，则z 的虚部为（ ） A. 1 B. 3 C.1- D.3-3. 已知向量),2,1(),,2(-==b m a 若22)2(m b b a a +=-⋅，则实数m 等于（ ）A.21B.25C.45 D.454. 已知32cos )2cos(157sin 59sin 15754++=-x x COS COS πππππ，则x 2s in 等于（ ） A.31 B.31- C.121 D.121-5. 执行如图所示的程序框图，若49=a ，则输出S 的值为（ ） A.10B.12C.14D.166. 若实数y x ,满足条件⎪⎩⎪⎨⎧≤-≥-+≥+-,01,022,01x y x y x 则y x z 345+-=的最大值为（ ）n m ,A.815-B. 45-C.21-D.1-7. “dx x m )34(221-≤⎰”是“函数m x x x f ++=212)(的值不小于4”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8. 甲、乙、丙三位同学将独立参加英语听力测试，根据平时训练的经验，甲、乙、丙三人能达标的概率分别为5332、、P ，若将三人中有人达标但没有全部达标的概率为32，则P 等于（ ） A.32 B.43 C.54 D.659. 已知函数)3cos(cos 21)(ϕ++=x x x f 是偶函数，其中ϕ)2,0(π∈，则下列关于函数)2c o s ()(ϕ-=x x g 的正确描述是（ ） A.)(x g 在区间]3,12[ππ-上的最小值为-1. B.)(x g 的图象可由函数)(x f 的图象先向上平移2个单位，在向右平移3π个单位得到. C.)(x g 的图象可由函数)(x f 的图象先向左平移3π个单位得到. D.)(x g 的图象可由函数)(x f 的图象先向右平移3π个单位得到.10. 已知函数⎩⎨⎧≥-=,1,1,10,2)(x x x f ＜＜则不等式5)1(log )14(log log 3412≤+--x f x x 的解集为（ ）A.)1,31( B.[1,4] C.)4,31( D.[1,∞+)11. 已知双曲线）＞，＞00(1:2222b a b y a x C =-的左焦点为F N M c 、),0,(-在双曲线C 上，O 是坐标原点，若四边形OFMN 为平行四边形，且四边形OFMN 的面积为cb 2，则双曲线C 的离心率为（ ）A.2B.2C.22D.3212. 已知函数ex exe x g x x xf x +=---=)(,36)(2，实数 满足m ＜n ＜0。

2017年四川省大教育联盟高考数学三诊试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知全集U，集合M，N满足M⊆N⊆U，则下列结论正确的是（）A．M∪N=U B．（∁U M）∪（∁U N）=U C．M∩（∁U N）=∅D．（∁U M）∪（∁U N）=∅2．（5分）已知复数z满足（2+i）z=2﹣i（i为虚数单位），则z在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．（5分）已知α是锐角，若cos（α+）=，则sin（α﹣）=（）A．﹣ B．﹣C．D．4．（5分）已知实数x，y满足不等式，则3x+2y的最大值为（）A．0 B．2 C．4 D．55．（5分）《九章算术》是我国古代内容极为丰富的数学名著，系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”，若某“阳马”的三视图如图所示（单位：cm），则该阳马的外接球的体积为（）A．100πcm3B．C．400πcm3D．6．（5分）运行如图所示的程序，若输出y的值为1，则输入x的值为（）A．0 B．0或﹣1 C．±1 D．17．（5分）设直角坐标平面内与两个定点A（﹣2，0），B（2，0）的距离之差的绝对值等于2的点的轨迹是E．过点B作与x轴垂直的直线l与曲线E交于C，D 两点，则=（）A．﹣9 B．﹣3 C．3 D．98．（5分）利用计算机产生120个随机正整数，其最高位数字（如：34的最高位数字为3，567的最高位数字为5）的频数分布图如图所示，若从这120个正整数中任意取出一个，设其最高位数字为d（d=1，2，…，9）的概率为P，下列选项中，最能反映P与d的关系的是（）A．P=lg（1+）B．P=C．P=D．P=×9．（5分）已知ω为正整数，函数f（x）=sinωxcosωx+在区间内单调递增，则函数f（x）（）A．最小值为，其图象关于点对称B．最大值为，其图象关于直线对称C．最小正周期为2π，其图象关于点对称D．最小正周期为π，其图象关于直线对称10．（5分）将正方形ABCD沿对角线BD折成直二面角后的图形如图所示，若E 为线段BC的中点，则直线AE与平面ABD所成角的余弦为（）A．B．C．D．11．（5分）在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的半圆分别交BA及其延长线于点M，N，点P在上运动（如图）．若，其中λ，μ∈R，则2λ﹣5μ的取值范围是（）A．[﹣2，2]B．C．D．12．（5分）已知椭圆M：（a＞b＞0）的一个焦点为F（1，0），离心率为，过点F的动直线交M于A，B两点，若x轴上的点P（t，0）使得∠APO=∠BPO总成立（O为坐标原点），则t=（）A．2 B．C．D．﹣2二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）从0，1，2，3，4五个数字中随机取两个数字组成无重复数字的两位数，则所得两位数为偶数的概率是．（结果用最简分数表示）14．（5分）曲线y=和直线y=x围成的图形面积是．15．（5分）在△ABC中，∠BAC=120°，AC=2AB=4，点D在BC上，且AD=BD，则AD=．16．（5分）已知函数f（x）=（x﹣1）e x+（其中a∈R）有两个零点，则a的取值范围是．三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）已知数列{a n}中，a2=2，其前n项和S n满足：（n ∈N*）．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若，求数列{b n}的前n项和T n．18．（12分）第96届（春季）全国糖酒商品交易会于2017年3月23日至25日在四川举办．交易会开始前，展馆附近一家川菜特色餐厅为了研究参会人数与餐厅所需原材料数量的关系，查阅了最近5次交易会的参会人数x （万人）与餐厅所用原材料数量t （袋），得到如下数据：（Ⅰ）请根据所给五组数据，求出t 关于x 的线性回归方程；（Ⅱ）已知购买原材料的费用C （元）与数量t （袋）的关系为投入使用的每袋原材料相应的销售收入为600元，多余的原材料只能无偿返还．若餐厅原材料现恰好用完，据悉本次交易会大约有14万人参加，根据（Ⅰ）中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？（注：利润L=销售收入﹣原材料费用）．（参考公式：=，）19．（12分）如图，三棱柱ABC ﹣A 1B 1C 1中，侧棱AA 1⊥底面ABC ，，AB ⊥AC ，D 是棱BB 1的中点． （Ⅰ）证明：平面A 1DC ⊥平面ADC ；（Ⅱ）求平面A 1DC 与平面ABC 所成二面角的余弦值．20．（12分）已知直线l的方程为y=x+2，点P是抛物线y2=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y2=4x交于点B．（Ⅰ）求点P的坐标；（Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．21．（12分）已知函数f（x）=alnx+b（a，b∈R），曲线f（x）在x=1处的切线方程为x﹣y﹣1=0．（Ⅰ）求a，b的值；（Ⅱ）证明：；（Ⅲ）已知满足xlnx=1的常数为k．令函数g（x）=me x+f（x）（其中e是自然对数的底数，e=2.71828…），若x=x0是g（x）的极值点，且g（x）≤0恒成立，求实数m的取值范围．[选修4-4：坐标系与参数方程]22．（10分）已知α∈[0，π），在直角坐标系xOy中，直线l1的参数方程为（t为参数）；在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，直线l2的极坐标方程是ρcos（θ﹣α）=2sin（α+）．（Ⅰ）求证：l1⊥l2（Ⅱ）设点A的极坐标为（2，），P为直线l1，l2的交点，求|OP|•|AP|的最大值．[选修4-5：不等式选讲]23．已知函数|﹣|，其中﹣3≤a≤1．（Ⅰ）当a=1时，解不等式f（x）≥1；（Ⅱ）对于任意α∈[﹣3，1]，不等式f（x）≥m的解集为空集，求实数m的取值范围．2017年四川省大教育联盟高考数学三诊试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知全集U，集合M，N满足M⊆N⊆U，则下列结论正确的是（）A．M∪N=U B．（∁U M）∪（∁U N）=U C．M∩（∁U N）=∅D．（∁U M）∪（∁U N）=∅【解答】解：∵全集U，集合M，N满足M⊆N⊆U，作出文氏图，如下：∴由文氏图得M∩（∁U N）=∅．故选：C．2．（5分）已知复数z满足（2+i）z=2﹣i（i为虚数单位），则z在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：由（2+i）z=2﹣i，得，∴z在复平面内对应的点的坐标为（），位于第四象限．故悬案：D．3．（5分）已知α是锐角，若cos（α+）=，则sin（α﹣）=（）A．﹣ B．﹣C．D．【解答】解：∵α是锐角，α+∈（，），且cos（α+）=，∴sin（α+）==，∴sin（α﹣）=sin[（α+）﹣]=sin（α+）cos﹣cos（α+）sin=﹣=．故选：C．4．（5分）已知实数x，y满足不等式，则3x+2y的最大值为（）A．0 B．2 C．4 D．5【解答】解：由约束条件作出可行域如图，联立，解得A（1，1），令z=3x+2y，化为y=﹣，由图可知，当直线y=﹣过A时，直线在y 轴上的截距最大，z有最大值为5．故选：D．5．（5分）《九章算术》是我国古代内容极为丰富的数学名著，系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”，若某“阳马”的三视图如图所示（单位：cm），则该阳马的外接球的体积为（）A．100πcm3B．C．400πcm3D．【解答】解：如图所示，该几何体为四棱锥P﹣ABCD．底面ABCD为矩形，其中PD⊥底面ABCD．AB=6，AD=2，PD=6．则该阳马的外接球的直径为PB====10．∴该阳马的外接球的体积==cm3．故选：B．6．（5分）运行如图所示的程序，若输出y的值为1，则输入x的值为（）A．0 B．0或﹣1 C．±1 D．1【解答】解：根据如图所示的程序语言知，该程序运行后输出函数y=；当x≥0时，y=2x=1，解得x=0；当x＜0时，y=|x|=1，解得x=﹣1；综上，输出y的值为1时，输入x的值为0或﹣1．故选：B．7．（5分）设直角坐标平面内与两个定点A（﹣2，0），B（2，0）的距离之差的绝对值等于2的点的轨迹是E．过点B作与x轴垂直的直线l与曲线E交于C，D 两点，则=（）A．﹣9 B．﹣3 C．3 D．9【解答】解：直角坐标平面内与两个定点A（﹣2，0），B（2，0）的距离之差的绝对值等于2，由双曲线的定义可得轨迹E是以A，B为焦点的双曲线，且c=2，a=1，b=，方程为x2﹣=1，x=2代入方程得：y=±3，可设C点的坐标为（2，3），D（2，﹣3），则=（4，3）•（0，﹣3）=4×0+3×（﹣3）=﹣9．故选：A．8．（5分）利用计算机产生120个随机正整数，其最高位数字（如：34的最高位数字为3，567的最高位数字为5）的频数分布图如图所示，若从这120个正整数中任意取出一个，设其最高位数字为d（d=1，2，…，9）的概率为P，下列选项中，最能反映P与d的关系的是（）A．P=lg（1+）B．P=C．P=D．P=×【解答】解：当d=5时，其概率为P==，对于B，P=，对于C，P=0，对于D，P=，故B，C，D均不符合，故选：A．9．（5分）已知ω为正整数，函数f（x）=sinωxcosωx+在区间内单调递增，则函数f（x）（）A．最小值为，其图象关于点对称B．最大值为，其图象关于直线对称C．最小正周期为2π，其图象关于点对称D．最小正周期为π，其图象关于直线对称【解答】解：∵f（x）=sinωxcosωx+=sin2ωx+﹣=sin （2ωx+），又∵f（x）在在区间内单调递增，∴由﹣≤2×（﹣）ω+，2×ω+≤，解得：ω≤，ω≤，∴由ω为正整数，可得ω=1，f（x）=sin（2x+），∴f（x）的最大值为，最小正周期为π，故A，C选项错误；∵令2x+=kπ+，k∈Z，解得：x=+，k∈z，可得当k=﹣1时，f（x）关于直线x=﹣对称．∴B选项错误，D选项正确．故选：D．10．（5分）将正方形ABCD沿对角线BD折成直二面角后的图形如图所示，若E 为线段BC的中点，则直线AE与平面ABD所成角的余弦为（）A．B．C．D．【解答】解：如图所示，取DB中点O，连接CO、AO，∵四边形ABCD为正方形，∴CO⊥DB．又∵面DCB⊥面ADB，∴CO⊥面ABD，过E作EH∥CO交DB于H，则有EH⊥面ADB．H为OB中点，连接AH，则∠EAH就是直线AE与平面ABD所成的角．设正方形ABCD的边长为2，则EH=，AH=，∴，cos∠EAH=，∴直线AE与平面ABD所成角的余弦为．故选：C．11．（5分）在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的半圆分别交BA及其延长线于点M，N，点P在上运动（如图）．若，其中λ，μ∈R，则2λ﹣5μ的取值范围是（）A．[﹣2，2]B．C．D．【解答】解：建立如图所示的坐标系，则A（0，0），B（2，0），D（0，1），C（2，2），E（2，1），F（1，1.5），P（co sα，sinα）（0≤α≤π），由=λ+μ得，（cosα，sinα）=λ（2，1）+μ（﹣1，）⇒cosα=2λ﹣μ，sinα=λ+⇒λ=，∴2λ﹣5μ=2（）﹣5（）=﹣2（sinα﹣cosα）=﹣2sin（）∵∈[﹣，]∴﹣2sin（）∈[﹣2，2]，即2λ﹣5μ的取值范围是[﹣2，2]．12．（5分）已知椭圆M：（a＞b＞0）的一个焦点为F（1，0），离心率为，过点F的动直线交M于A，B两点，若x轴上的点P（t，0）使得∠APO=∠BPO总成立（O为坐标原点），则t=（）A．2 B．C．D．﹣2【解答】解：由题意可知c=1，椭圆的离心率e==，则a=，b2=a2﹣c2=1，∴椭圆的标准方程：，当直线AB斜率不存在时，t可以为任意非零实数，当直线AB的斜率存在时，设AB的方程为y=k（x﹣1），设A（x1，y1），B（x1，y1），则，整理得：（1+2k2）x2﹣4k2x+2k2﹣2=0，则x1+x2=，x1x2=，由∠APO=∠BPO，则直线PA与PB的斜率之和为0，则+=0，整理得：2x1x2﹣（t+1）（x1+x2）+2t=0，∴2×﹣（t+1）×+2t=0，解得：t=2，二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）从0，1，2，3，4五个数字中随机取两个数字组成无重复数字的两位数，则所得两位数为偶数的概率是．（结果用最简分数表示）【解答】解：从0，1，2，3，4五个数字中随机取两个数字组成无重复数字的两位数，基本事件总数n=4×4=16，所得两位数为偶数包含的基本事件的个数m=4×1+2×3=10， ∴所得两位数为偶数的概率p=．故答案为：．14．（5分）曲线y=和直线y=x 围成的图形面积是．【解答】解：曲线和直线y=x 交点为：（1，1），所以围成的图形面积为=（）|=；故答案为：．15．（5分）在△ABC 中，∠BAC=120°，AC=2AB=4，点D 在BC 上，且AD=BD ，则AD=．【解答】解：∵在△ABC 中，∠BAC=120°，AC=2AB=4，∴由余弦定理得BC==2，由正弦定理，得：，∴sinB===，∴cosB==，∵AD=BD ，∴设AD=BD=x ，由余弦定理得：cosB==，∴AD=x==．故答案为：．16．（5分）已知函数f（x）=（x﹣1）e x+（其中a∈R）有两个零点，则a的取值范围是（﹣∞，﹣1）∪（﹣1，0）．【解答】解：f′（x）=）=（x﹣1）e x+e x+ax=x（e x+a），①当a≥0时，e x+a＞0，∴x∈（﹣∞，0）时，f′（x）＜0，x∈（0，+∞）时，f′（x）＞0，f（x）在（﹣∞，0）递减，在（0，+∞）递增，且f（0）=0，此时f（x）=（x﹣1）e x+（其中a∈R）不存在有两个零点；②当a=﹣1时，f′（x）≥0恒成立，函数f（x）单调，此时f（x）=（x﹣1）e x+（其中a∈R）不存在有两个零点；③当a＜0且a≠﹣1时，令f′（x）=0，解得x1=0，x2=ln（﹣a）（a≠﹣1）．a∈（﹣1，0）时，x2＜0，函数在（﹣∞，ln（﹣a）））递增，在（ln（﹣a），0）递减，在（0，+∞）递增，而f（0）=0，此时函数恰有两个零点；a∈（﹣∞，﹣1），时，x2＞0，函数在（﹣∞，0）递增，在（0，ln（﹣a））递减，在（ln（﹣a），+∞）递增，而f（0）=0，此时函数恰有两个零点；综上，则a的取值范围是：（﹣∞，﹣1）∪（﹣1，0）故答案为：（﹣∞，﹣1）∪（﹣1，0）三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）已知数列{a n}中，a2=2，其前n项和S n满足：（n ∈N*）．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若，求数列{b n}的前n项和T n．【解答】解：（Ⅰ）由题意有．所以，则有（n≥2），所以2（S n﹣S n﹣1）=na n﹣（n﹣1）a n﹣1，即（n﹣2）a n=（n﹣1）a n﹣1（n≥2）．所以（n﹣1）a n+1=na n，两式相加得2（n﹣1）a n=（n﹣1）（a n+1+a n﹣1），即2a n=a n+1+a n﹣1（n≥2），即a n+1﹣a n=a n﹣a n﹣1（n≥2，n∈N），故数列{a n}是等差数列．又a1=0，a2=2，所以公差d=2，所以数列{a n}的通项公式为a n=2n﹣2．（Ⅱ）由（Ⅰ）知，则…+n•22n﹣2，两边同乘以22得+…+（n﹣1）•22n﹣2+n•22n，两式相减得+22n﹣2﹣n•22n，即=，所以．18．（12分）第96届（春季）全国糖酒商品交易会于2017年3月23日至25日在四川举办．交易会开始前，展馆附近一家川菜特色餐厅为了研究参会人数与餐厅所需原材料数量的关系，查阅了最近5次交易会的参会人数x（万人）与餐厅所用原材料数量t（袋），得到如下数据：（Ⅰ）请根据所给五组数据，求出t关于x的线性回归方程；（Ⅱ）已知购买原材料的费用C （元）与数量t （袋）的关系为投入使用的每袋原材料相应的销售收入为600元，多余的原材料只能无偿返还．若餐厅原材料现恰好用完，据悉本次交易会大约有14万人参加，根据（Ⅰ）中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？（注：利润L=销售收入﹣原材料费用）．（参考公式：=，）【解答】解：（Ⅰ）由数据，求得，，10×25+12×29=1273，102+122=510，=，，∴t 关于x 的线性回归方程为．（Ⅱ）由（Ⅰ）中求出的线性回归方程，当x=14时，，即预计需要原材料34.2袋，∵∴，若t＜35，利润L=600t﹣（300t+20）=300t﹣20，当t=34时，利润L max=300×34﹣20=10180元；若t≥35，利润L=600×34.2﹣290t=20520﹣290t，当t=35时，利润L max=20520﹣290×35=10370元；综上所述，该餐厅应购买35袋原材料，才能获得最大利润，最大利润是10370元．19．（12分）如图，三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，，AB⊥AC，D是棱BB1的中点．（Ⅰ）证明：平面A1DC⊥平面ADC；（Ⅱ）求平面A1DC与平面ABC所成二面角的余弦值．【解答】（Ⅰ）证明：∵侧棱AA1⊥底面ABC，∴AA1⊥AC，又∵AB⊥AC，AB∩AC=A，∴AC⊥平面ABB1A1，∵A1D⊂平面ABB1A1，∴AC⊥A1D，设AB=a，由，AB⊥AC，D是棱BB1的中点．得，AA 1=2a，则+，∴AD⊥A1D，∵AD∩AC=A，∴A1D⊥平面ADC．又∵A1D⊂平面A1DC，∴平面A1DC⊥平面ADC；（Ⅱ）解：如图所示，分别以AB，AC，AA1所在直线为x，y，z轴建立空间直角坐标系，不妨设AB=1，则A（0，0，0），D（1，0，1），C（0，1，0），A1（0，0，2）．显然是平面ABC的一个法向量，设平面A 1DC的法向量，由令z=1，得平面A 1DC的一个法向量，∴=，即平面A1DC与平面ABC所成二面角的余弦值为．20．（12分）已知直线l的方程为y=x+2，点P是抛物线y2=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y2=4x交于点B．（Ⅰ）求点P的坐标；（Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．【解答】解：（Ⅰ）设点P的坐标为（x0，y0），则，所以，点P到直线l的距离．当且仅当y0=2时等号成立，此时P点坐标为（1，2）．…（4分）（Ⅱ）设点A的坐标为，显然y1≠2．当y1=﹣2时，A点坐标为（1，﹣2），直线AP的方程为x=1；可得B（，3），直线AB：y=4x﹣6；当y1≠﹣2时，直线AP的方程为，化简得4x﹣（y1+2）y+2y1=0；综上，直线AP的方程为4x﹣（y1+2）y+2y1=0．与直线l的方程y=x+2联立，可得点Q的纵坐标为．因为，BQ∥x轴，所以B点的纵坐标为．因此，B点的坐标为．当，即时，直线AB的斜率．所以直线AB的方程为，整理得．当x=2，y=2时，上式对任意y1恒成立，此时，直线AB恒过定点（2，2），也在y=4x﹣6上，当时，直线AB的方程为x=2，仍过定点（2，2），故符合题意的直线AB恒过定点（2，2）．…（13分）21．（12分）已知函数f（x）=alnx+b（a，b∈R），曲线f（x）在x=1处的切线方程为x﹣y﹣1=0．（Ⅰ）求a，b的值；（Ⅱ）证明：；（Ⅲ）已知满足xlnx=1的常数为k．令函数g（x）=me x+f（x）（其中e是自然对数的底数，e=2.71828…），若x=x0是g（x）的极值点，且g（x）≤0恒成立，求实数m的取值范围．【解答】解：（Ⅰ）f（x）的导函数，由曲线f（x）在x=1处的切线方程为x﹣y﹣1=0，知f'（1）=1，f（1）=0，所以a=1，b=0．（Ⅱ）令=，则=，当0＜x＜1时，u'（x）＜0，u（x）单调递减；当x＞1时，u'（x）＞0，u（x）单调递增，所以，当x=1时，u（x）取得极小值，也即最小值，该最小值为u（1）=0，所以u（x）≥0，即不等式成立．（Ⅲ）函数g（x）=me x+lnx（x＞0），则，当m≥0时，g'（x）＞0，函数g（x）在（0，+∞）内单调递增，g（x）无极值，不符合题意；当m＜0时，由，得，结合y=e x，在（0，+∞）上的图象可知，关于x的方程一定有解，其解为x0（x0＞0），且当0＜x＜x0时，g'（x）＞0，g（x）在（0，x0）内单调递增；当x＞x0时，g'（x）＜0，g（x）在（x0，+∞）内单调递减．则x=x0是函数g（x）的唯一极值点，也是它的唯一最大值点，x=x0也是g'（x）=0在（0，+∞）上的唯一零点，即，则．所以g（x）max=g（x0）==．由于g（x）≤0恒成立，则g（x）max≤0，即，（*）考察函数，则，所以h（x）为（0，+∞）内的增函数，且，，又常数k满足klnk=1，即，所以，k是方程的唯一根，于是不等式（*）的解为x0≤k，又函数（x＞0）为增函数，故，所以m的取值范围是．[选修4-4：坐标系与参数方程]22．（10分）已知α∈[0，π），在直角坐标系xOy中，直线l1的参数方程为（t为参数）；在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，直线l2的极坐标方程是ρcos（θ﹣α）=2sin（α+）．（Ⅰ）求证：l1⊥l2（Ⅱ）设点A的极坐标为（2，），P为直线l1，l2的交点，求|OP|•|AP|的最大值．【解答】解：（Ⅰ）证明：直线l1的参数方程为（t为参数）；消去参数t可得：直线l1的普通方程为：xsinα﹣ycosα=0．又直线l2的极坐标方程是ρcos（θ﹣α）=2sin（α+）．展开为ρcosθcosα+ρsinθsinα=2sin（α+）．即直线l 2的直角坐标方程为：xcosα+ysinα﹣2sin（α+）=0．因为sinαcosα+（﹣cosα）sinα=0，根据两直线垂直的条件可知，l1⊥l2．（Ⅱ）当ρ=2，时，ρcos（θ﹣α）=2cos=2sin（α+）．所以点A（2，），在直线ρcos（θ﹣α）=2sin（α+）上．设点P到直线OA的距离为d，由l1⊥l2可知，d的最大值为=1．于是|OP|•|AP|=d•|OA|=2d≤2所以|OP|•|AP|的最大值为2．[选修4-5：不等式选讲]23．已知函数|﹣|，其中﹣3≤a≤1．（Ⅰ）当a=1时，解不等式f（x）≥1；（Ⅱ）对于任意α∈[﹣3，1]，不等式f（x）≥m的解集为空集，求实数m的取值范围．【解答】解：（Ⅰ）当a=1时，f（x）=|x+2|﹣|x|，①当x＜﹣2时，不等式即为﹣x﹣2+x≥1，不等式无解；②当﹣2≤x≤0时，不等式即为x+2+x≥1，解得；③当x＞0时，不等式即为x+2﹣x≥1，不等式恒成立．综上所述，不等式的解集是．（Ⅱ）由．而=4+4=8，∴，∴．要使不等式f （x ）≥m 的解集为空集，则有，所以，实数m 的取值范围是．赠送初中数学几何模型【模型一】“一线三等角”模型： 图形特征：60°60°60°45°45°45°运用举例：1.如图，若点B 在x 轴正半轴上，点A (4，4)、C (1，－1)，且AB ＝BC ，AB ⊥BC ，求点B 的坐标；xyB CAO2.如图，在直线l 上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ，则14S S += ．ls 4s 3s 2s 13213. 如图，Rt △ABC 中，∠BAC =90°，AB =AC =2，点D 在BC 上运动（不与点B ，C 重合），过D 作∠ADE =45°，DE 交AC 于E ． （1）求证：△ABD ∽△DCE ；（2）设BD =x ，AE =y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围； （3）当△ADE 是等腰三角形时，求AE 的长．EB4.如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。

数学（理）试题 第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合{}{}2|4120,|2A x x x B x x =--<=>,则A B =（ ）A ．3,62⎛⎫⎪⎝⎭ B ． 3,22⎛⎫⎪⎝⎭C ．()1,6D ．()1,2 2.若复数()421aiz a R i-=∈-的实部为1，则z 的虚部为 （ ） A ．1 B ．3 C ．1- D ．3- 3. 已知向量()()2,,1,2a m b ==-，若()222a a b b m -=+，则实数m = （ ）A ．12 B ．52 C ．4D ．54 4. 巳知47972coscos sin sin cos cos 51551523x x πππππ⎛⎫-=++ ⎪⎝⎭，则sin 2x =（ ） A ．13 B ． 13- C. 112 D ．112- 5. 执行如图所示的程序框图，输出S 的值为（ ）A ．14B ．20 C. 30 D ．556. 若实数,x y 满足条件1022010x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩，则543z x y =-+的最大值为 （ ）A ．158-B ．54- C.12- D ．1- 7. “()22143m x dx ≤-⎰”是“函数()122xx m f x +=+的值不小于4” 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．即不充分也不必要条件8. 甲、乙、丙三位同学将独立参加英语听力测试，根据平时训练的经验，甲、乙、丙三人能达标的概率分别为23,,35P ，若三人中有人达标但没有全部达标的概率为23，则P =（ ） A ．23 B ．34 C.45 D ．569. 已知函数()()12cos cos 3f x x x ϕ=++是偶函数，其中0,2πϕ⎛⎫∈ ⎪⎝⎭，则下列关于函数()()cos 2g x x ϕ=-的正确描述是 （ ）A ．()g x 在区间上,123ππ⎡⎤-⎢⎥⎣⎦的最小值为1- B ．()g x 的图象可由函数()f x 的图象先向上平移2个单位，再向右平移3π个单位得到 C. ()g x 的图象可由函数()f x 的图象向左平移3π个单位得到 D ．()g x 的图象可由函数()f x 的图象向右平移3π个单位得到10. 已知函数()2,011,1x f x x -<<⎧=⎨≥⎩，则不等式()2134log log 41log 15x x f x ⎛⎫--+≤ ⎪⎝⎭的解集为（ ）A ．1,13⎛⎫⎪⎝⎭ B ．[]1,4 C. 1,43⎛⎫ ⎪⎝⎭D ．[)1,+∞11. 已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为(),0,,F c M N -在双曲线C 上，O是坐标原点，若四边形OFMN 为平行四边形，且四边形OFMN，则双曲线C的离心率为（ ）A ．2 C. ．12. 已知函数()()263,x e exf x x xg x ex+=---=，实数,m n 满足0m n <<，若[]()12,,0,x m n x ∀∈∃∈+∞，使得()()12f x g x =成立，则n m -的最大值为 （ ）A ．4B ．．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 51x ⎛⎫- ⎪⎝⎭的展开式中的常数项为 __________.14. 若抛物线()220y px p =>上的点()00,22p x x ⎛⎫> ⎪⎝⎭到其焦点的距离为52，则p = __________.15. 已知等差数列{}n a 的前n 项和为n S ，且3634a a =+，若510S <，则2a 的取值范围是 _________.16. 在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ，22sin cos sin cos 4sin ,cos c A A a C C B B D +==是AC 上一点，且23BCD S ∆=，则ADAC= _________. 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）已知数列{}n a 的前n 项和为n S ，且()163n n S a n N +*=+∈.（1）求a 的值及数列{}n a 的通项公式；（2）设 ()()2311log n nn b an a a +=-，求1n b ⎧⎫⎨⎬⎩⎭的前n 项和为n T .18.（本小题满分12分）在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ，且232cos cos a c bA B-=.（1）若b B =,求a ； （2）若a ABC =∆求b c +. 19.（本小题满分12分）为推行“新课堂”教学法，某化学老师分別用原传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班进行教学实验，为了解教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图，记成绩不低于70分者为“成绩优良”.（1）由以上统计数据填写下面22⨯列联表，并判断能否在犯错误的摡率不超过0.025的前提下认为“成绩优良与教学方式有关” ？ 附:()()()()()22n ad bc K a b a d a c b d -=++++，其中n a b c d =+++独立性检验临界表（2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法来抽取8人进行考核，在这8人中，记成绩不优良的乙班人数为X ，求X 的分布列及数学期望.20.（本小题满分12分）已知右焦点为(),0F c 的椭圆()2222:10x y M a b a b +=>>过点31,2⎛⎫⎪⎝⎭，且椭圆M 关于直线x c =对称的图形过坐标原点. （1）求椭圆M 的方程；（2）过点()4,0且不垂直于y 轴的直线与椭圆M 交于,P Q 两点，点Q 关于x 轴的对称点为E ，证明: 直线PE 与x 轴的交点为F .21.（本小题满分12分）已知函数()()()322ln f x a x a x a R =--+-∈. （1）若函数()y f x =在区间()1,3上单调，求a 的取值范围 ； （2）若函数()()g x f x x =-在10,2⎛⎫ ⎪⎝⎭上无零点， 求a 的最小值. 请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分. 22.（本小题满分10分）选修4-4：坐标系与参数方程已知极点与直角坐标系的原点重合 ，极轴与x 轴的正半轴重合，圆C 的极坐标是2sin a ρθ=，直线l 的参数方程是35(45x t a t y t ⎧=-+⎪⎪⎨⎪=⎪⎩为参数）. （1）若2,a M =为直线l 与x 轴的交点，N 是圆C 上一动点，求MN 的最大值； （2）若直线l 被圆C截得的弦长为求a 的值 . 23.（本小题满分10分）选修4-5：不等式选讲 设函数()1f x x =+. （1）解不等式()2f x x <； （2） 若()28f x x a+->对任意x R ∈恒成立，求实数a 的取值范围.四川省2017届高三上学期巴蜀黄金大联考数学（理）试题参考点案一、选择题（每小题5分，共60分）1-5. CBDAC 6-10.CABCC 11-12.DA 二、填空题（每小题5分，共20分）13. 20- 14. 1 15. (),2-∞ 16. 59三、解答题 17.解：（1）163,n n S a +=+∴当1n =时，11669S a a ==+；当2n ≥时，()16623n n n n a S S -=-= ，即{}13,n n n a a -=∴是等比数列，11a ∴=，则96a +=，得3,a =-∴数列{}n a 的通项公式为()13n n a n N -*=∈.()2sin cos 3sin cos 2sin cos ,2sin cos sin cos 2sin 3sin cos A B C A B A A B B A C C A=-∴+== ，2sin 0,cos 3C A ≠∴=，则sin 5sin ,3A bB ==∴由正弦定理得：5sin sin 3b a AB ==.（2）ABC ∆的面积为1sin 222bc A ∴=，得()2224103,6,6,633bc a b c bc b c bc ==∴+-=∴+-=，即()216,0,0,4b c b c b c +=>>∴+=.19.解：（1）根据22⨯列联表中的数据，得2K 的观测值为()240941611 5.227 5.024,25152020k ⨯-⨯=≈>∴⨯⨯⨯能在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”. （2）由表可知在8人中成绩不优良的人数为158340⨯=，则X 的可能取值为0,1,2,3. ()()()()32112311114114433331515151533446640;1;2;39191455455C C C C C C P X P X PX P X C C C C ============.X ∴的分布列为：()01239191455455455E X ∴=⨯+⨯+⨯+⨯=.20.解：（1）椭圆M 过点223191,,124a b ⎛⎫∴+= ⎪⎝⎭， ① 椭圆M 关于直线x c =对称的图形过坐标原点，2222232,,4a c abc b a ∴==+∴=， ② 由①②得224,3,a b ==∴椭圆M 的方程为22143x y +=. （2）证明：易知直线PQ 的斜率必存在，设直线PQ 的的方程为()()40y k x k =-≠，代人22143x y +=得()2222343264120k x k x k +-+-=，由()()()2222324364120kk k ∆=--+->得，11,22k ⎛⎫∈- ⎪⎝⎭，设()()()112222,,,,,P x y Q x y E x y -，则22121222326412,3434k k x x x x k k -+==++，则直线PE 的方程为()1212112y y y y x x x x +-=--，令0y =得：()()()122112122111121212448x k x x k x x x x y x y x y x y y y y k x x -+--+=-+==+++- ()222212122122641232242434341328834k k x x x x k k k x x k ---+++===+--+， ∴直线PE 过定点()1,0，又M 的右焦点为()1,0，∴直线PE 与x 轴的交点为F . 21.解：（1）()()322'3a x f x a x x--=--=,当3a ≥时，()'0f x <，即函数()f x 在区间()1,3上单调递减，当3a <时，令()'0f x =，得23x a =-，若函数()y f x =在区间()1,3上单调递增，则213a ≤-或233a ≥-，解得1a ≤或733a ≤<；综上，a 的取值范围是(]7,1,3⎡⎫-∞+∞⎪⎢⎣⎭. （2）因为当0x →时，()g x →+∞，所以()()()212ln 0g x a x x =---<在区间10,2⎛⎫ ⎪⎝⎭上恒成立不可能，故要使函数()g x 在10,2⎛⎫ ⎪⎝⎭上无零点，只要对任意的()10,,02x g x ⎛⎫∈> ⎪⎝⎭上恒成立，即对12ln 0,,221x x a x ⎛⎫∈>-⎪-⎝⎭恒成立，令()2ln 12,0,12x l x x x ⎛⎫=-∈ ⎪-⎝⎭，则()()()()222212ln 2ln 2'11x x x x x l x x x --+-=-=--，再令()212ln 2,0,2m x x x x ⎛⎫=+-∈ ⎪⎝⎭，则 ()()222122'0x m x x x x --=-+=<，故()m x 在10,2⎛⎫⎪⎝⎭上为减函数，于是()122ln 202m x m ⎛⎫>=-> ⎪⎝⎭，从而，()'0l x >，()l x 在10,2⎛⎫⎪⎝⎭上为增函数，所以()124ln 22l x l ⎛⎫<=- ⎪⎝⎭，故要使2ln 21x a x >--上恒成立，只要[)24ln 2,a ∈-+∞，综上，()g x 在10,2⎛⎫⎪⎝⎭上无零点，则a 的最小值为24ln 2-.22.解：（1）由24sin ρρθ=得圆C 可化为2240x y y +-=， 将直线l 的参数方程化为直角坐标方程，得()423y x =--，令0y =，得2x =，即点M 的坐标为()2,0.又圆C 的圆心坐标为()0,2，半径2r =，则MC =MN 的最大值为2MC r +=.（2）因为圆()222:C x y a a +-=，直线:4340l x y a +-=，所以圆心C 到直线l 的距离为34,55a a ad -==∴==52a =±. 23.解：（1） 由()2f x x <得12x x +<，则212x x x -<+<，即1212x xx x+<⎧⎨+>-⎩，解得1,x >∴不等式()2f x x <的解集为()1,+∞. （2）()111f x x a x x a x x a a +-=++-≥+-+=+,又()3282f x x a+->=对任意x R ∈恒成立，即()3f x x a +->对任意x R ∈恒成立，13a ∴+>，解得4a <-或2a >，∴实数a 的取值范围是()(),42,-∞-+∞.。