华科船舶静力学大作业

格式：ppt
大小：5.51 MB
文档页数：42

下载文档原格式

华南理工大学_814船舶静力学2004--2017年_考研真题

第
2 页
4.（13 分）某内河船的排水量=580t，重心高 zG=2.5m,浮心高 zC=1.56m，该船各横倾角的形状稳性力臂如下表： 10 20 30 40 50 60 0 ls(m) 0.390 0.715 0.970 1.110 1.150 1.130 请列表计算和绘制出静稳性臂曲线和动稳性臂曲线，根据所绘制的静稳性臂曲线和动稳性臂曲线求出：（1）最大复原力臂、最大复原力矩、极限静倾角。（2）该船正浮时（ϕ0=0o），在外力作用下所能承受的最大动倾力矩以及与之对应的动倾角。（3）当横摇角 ϕ0=-15o 时，在外力作用下所能承受的最大动倾力矩和与之对应的动倾角。
814
华南理工大学 2017 年攻读硕士学位研究生入学考试试卷
（试卷上做答无效，请在答题纸上做答，试后本卷必须与答题纸一同交回）科目名称：船舶静力学适用专业：船舶与海洋工程；船舶与海洋工程（专硕）共 3 页一、填空题（每小题 1.5 分，共 15 分） 1.梯形法基本原理是：用若干直线段组成的近似地代替曲线，即以若干梯形面积之和来代替曲线下所包围的面积。 2.船舶漂浮的平衡条件为；。 3. 军用舰艇五种典型的排水量为：、标准排水量、、满载排水量、。 4.对于民用船舶来说，两种最基本的典型排水量为：和。 5.船舶由淡水驶入海水时，不变，发生了变化，还有可能发生。 6.在等体积倾斜的情况下，的交线必然通过原水线面的。 7.静水力曲线是将船舶在正浮状态的与之间的函数关系绘制在同一张图上。 8.利用曲线可方便地求得船舶在纵倾状态下的。 9.从动稳性角度考虑，在船舶倾斜过程中当稳性力矩等于外力矩时，船舶仍不能终止倾斜是因为大于。 10.大倾角静稳性臂公式 l=lb-lg 中，lb 称为，lg 称为。二、名词解释（每小题 2.5 分，共 25 分） 1 三舱制船 2.极限动横倾角 3.棱形系数 4.损失浮力法 5.正浮 6.稳性消失角 7.设计水线长

船舶静力学习题答案

Exercise 1-3
某内河驳船的水下体积V=4400m3，吃水d=2.6m，方形系数Cb=0.815，水线面系数Cw=0.882，求水线面面积Aw。
已知：Cb=0.815;Cw=0.882;V=4400t 解：Cvp=Cb/Cw=0.815/0.882=0.924
∵Cvp=V/(Aw.d) ∴Aw=V/(Cvp.d)=4400/(0.924*2.6)=1831.5 m2
Exercise 1-1
∵Am=πr2/2 Aw=2*0.2*4r*r=4r2 V=1/3(πr2)*2r=2/3 πr3
∴Cm=Am/(2r*r)= π/4=0.785 Cp=V/(1/2πr2*4r)= 1/3=0.333 Cwp=Aw /(4r*2r)= 1/2=0.500 Cb=V/(4r*2r*r)=π/12=0.261 Cvp=V/(4r2*r)=π/6=0.522
船舶静力学作业
船舶静力学习题答案
响砂山月牙泉
Exercise 1-1
1-1 两相等的正圆锥体在底部处相连接，每个锥体的高等于其底部直径．这个组合体浮于水面，使其两个顶点在水表面上，试绘图并计算：（1）中横剖面系数Cm，（2）纵向棱形系数Cp，（3）水线面系数Cw，（4）方形系数Cb。
V=(A *h)/3 d
Exercise 1-4源自各站型值：Bx2
y2[1(0.5L)2]
序
0
1
2
3
4
5
6
7
8
9
10
x -30
-24
-18
-12
-6
0
6
12
18
24
30
y
0
1.512 2.688 3.528 4.032 4.2 4.032 3.528 2.688 1.512

华科大有限元分析题及大作业题答案——船海专业(DOC)

（1）NDIV取5时的常应变三节点单元（单元数23）
图1-9(a)NDIV为5的网格划分及约束受载图
图1-9(b)NDIV为5的位移分布图
图1-9(c)NDIV为5的应力分布图
（2）NDIV为10的常应变三节点单元（单元数80）
图1-10(a)NDIV为10的网格划分及约束受载图
图1-10(b)NDIV为10的位移分布图
姓名：
学号：
班级：
有限元分析及应用作业报告
一、问题描述
图示无限长刚性地基上的三角形大坝，受齐顶的水压力作用，试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析，并对以下几种计算方案进行比较：
1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算；
2)分别采用不同数量的三节点常应变单元计算；
3）定义材料参数
4）生成几何模
a. 生成特征点
b.生成坝体截面
5）网格化分：划分网格时，拾取所有线段设定input NDIV 为10，选择网格划分方式为Tri+Mapped，最后得到200个单元。
6)模型施加约束：
约束采用的是对底面BC全约束。
大坝所受载荷形式为Pressure，作用在AB面上，分析时施加在LAB上，方向水平向右，载荷大小沿LAB由小到大均匀分布（见图1-2）。以B为坐标原点，BA方向为纵轴y，则沿着y方向的受力大小可表示为：
（Hale Waihona Puke ）其中ρ为水的密度，取g为9.8m/s2，可知Pmax为98000N，Pmin为0。施加载荷时只需对LAB插入预先设置的载荷函数（1）即可。
网格划分及约束受载情况如图1-3(a)和1-4(a)所示。
7）分析计算
8）结果显示
四、计算结果及结果分析

船舶静力学习题答案共60页

船舶静力学习题答案
11、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克
谢谢！
51、天下之事常成等于是呼吸，生命是活动。——卢梭
53、伟大的事业，需要决心，能力，组织和责任感。 ——易卜生 54、唯书籍不朽。——乔特
55、为中华之崛起而读书。 ——周恩来

船舶静力学讲稿

绪论船舶静力学是研究船舶航海性能的科学，是船舶设计与制造专业的一门重要专业技术基础课程，本学科要求有《高等数学》、《材料力学》、《理论力学》、《流体力学》等学科作为基础，也是今后学习《船舶强度与结构规范设计》、《船舶设计原理》、《造船工艺学》等课程的基础，因此要求同学们重视这门课的学习。

本课程包括六章。

其中第六章船舶的下水计算因在造船工艺学有阐述故在船舶静力学中不加以阐述。

第二、三、四章是重点章节。

通过本课程的学习，学生应对船舶浮性、稳性、抗沉性有一个全面的了解，在船舶设计时保证船舶具有合理的浮态（船舶在静水中的平衡状态，参数有吃水d、横倾角θ以及纵倾角ψ）和足够的稳性和抗沉性，同时学生应掌握衡量船舶稳性、浮性、抗沉性各种指标及其计算方法，能在设计时提供各种必要的计算说明书和曲线等数据。

一、船舶原理的内容船舶原理是研究船舶航海性能的科学。

（1）浮性——船舶在一定的装载情况下浮于一定水面位臵的能力（保持平衡位臵能力）。

（2）稳性——船舶在外力作用下，船舶发生倾斜而不致倾覆，当外力的作用消失后，仍能回到原来的平衡位臵的能力。

（3）抗沉性——当船体破损，海水进入舱室，船舶仍能保持一定的浮性和稳性而不致沉没和倾覆的能力。

（4）船舶快速性（速航性）——船舶尽可能消耗低的功率而达到一定航速的能力，包括船舶阻力与推进两部分，前者研究船舶在航行过程所遭受的各种阻力。

后者是研究克服阻力的推进器及其与船体间的相互作用（推力减额和伴流分数）。

（5）适航性（或称耐波性）——船舶在风流情况下的运动性能，主要研究船舶的横摇（rolling）、纵摇(pithing)、升沉等习惯上称为摇荡（摇摆、振荡）（6）操纵性——包括航向稳定性和船舶机动性(航向稳定性和船舶机动性是相互制约的，对船体的要求也是相互制约的)是按照驾驶员的意图保持原定航向和改变航向的能力。

船舶原理=船舶静力学+船舶动力学船舶静力学是以流体静力学为基础，研究船舶在不同条件下的浮性、稳性、抗沉性等问题。

华南理工大学《814船舶静力学》考研专业课真题试卷

四、计算题（50 分） 1.（5 分）已知某游艇的排水体积 =30 m3，长宽比 L/B=5，宽度吃水比 B/d=2.8，方形系数 CB=0.53。试求该游艇的主尺度 L，B 和 d。 2.（13 分）某海船船长 L=110 m，首吃水 dF=4.6 m，尾吃水 dA=5.1 m，每厘米吃水吨数 TPC=97 t/cm，每厘米纵倾力矩 MTC=102 tm/cm，漂心纵坐标 xF=-3.8 m。今在船上装载 100t 的货物，问装在何处可使船平浮？
第
1 页
3.（7 分）某海船水线间距为 0.5m，各水线对应的水线面积为： 0 1 2 3 水线 WL
4
42 151 194 242 242 水线面积 AW(m2) 求吃水为 2.0 m 时的排水体积，浮心垂向坐标 KB，垂向掕形系数 CVP 及每厘米吃水吨数 TPC. 4. (12 分)已知某驳船的船长 L=50 m，吃水 d=3 m，排水体积=735 m3，重心垂向坐标 KG=2.81m，浮心垂向坐标 KB 可按下式估算： KB
二、简答题（42 分） 1. 提高数值积分的方法有哪些？ 2. 何谓邦戎曲线？它有什么用途？ 3. 衡量船舶初稳性好坏的主要指标是什么？如何应用它判断船舶的稳定性？为什么船通常是横向倾覆而不是纵向倾覆？ 4. 船舶进水舱可分为哪几类？各有什么特点？μ=0.85 表示什么意思？ 5. 船舶在纵向重力下水方式过程中，船尾上浮是船舶下水过程中必然发生的现象；该现象出现在下水过程中的哪个阶段？可能出现哪些不利影响？可采取什么措施消除不利的影响？ 6. 静稳性曲线有哪些特征？三、问答题（34 分） 1. 什么是船舶静水力曲线？它包括哪几种性质的曲线？静水力曲线有什么用途？ 2. 船舶因重量移动产生了一个初始横倾角Φ0 ，现在船再受到一阵风作用，问阵风自出水舷吹来危险？还是自入水舷吹来危险？请作图说明原因。

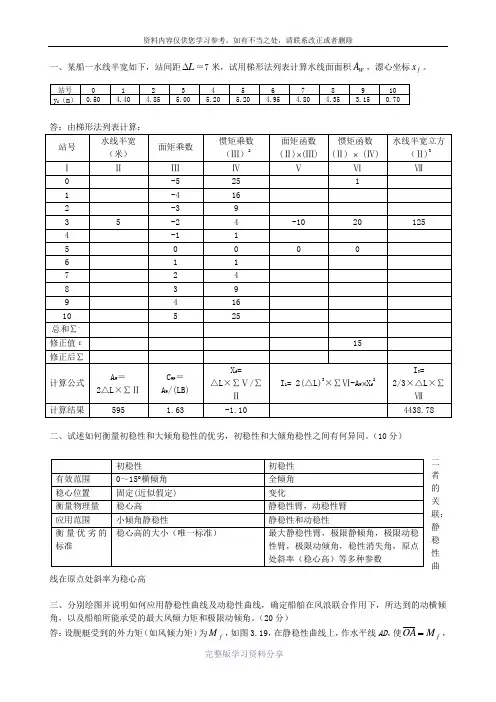
船舶静力学大题汇总

一、某船一水线半宽如下，站间距L ∆＝7米，试用梯形法列表计算水线面面积W A ，漂心坐标f x 。

答：由梯形法列表计算：二、试述如何衡量初稳性和大倾角稳性的优劣，初稳性和大倾角稳性之间有何异同。

（10分）二者的关联：静稳性曲线在原点处斜率为稳心高三、分别绘图并说明如何应用静稳性曲线及动稳性曲线，确定船舶在风浪联合作用下，所达到的动横倾角，以及船舶所能承受的最大风倾力矩和极限动倾角。

（20分）答：设舰艇受到的外力矩（如风倾力矩）为f M ，如图3.19，在静稳性曲线上，作水平线AD ，使f M OA =，并移动垂线CD 使BCD OAB S S =，即可确定动横倾角d φ。

但是，由于要凑得两块面积相等，实际操作比较麻烦，故通常直接应用动稳性曲线来确定d φ。

φM R (l)o BA CφdoT R (ld )φM fDM fm a x φd57.3o M fM fm a xφd m a x φd m a x C 'A 'B 'D 'NC 1D 1图1 静、动稳性曲线的应用横倾力矩fM所作的功为 φφd M T f f ⎰=0由于fM为常数，所以fT 为一直线，其斜率为fM，故当1=φ弧度＝53.3°时，ff M T =。

因此，在动稳性曲线上的横坐标=φ°处作一垂线，并量取f M得N 点，连接ON ，则直线ON 即为f T 随φ而变的规律。

fT 与TR 两曲线的交点C1表示横倾力矩fM所作的功与复原力矩MR 所作的功相等。

与C1点相对应的倾角即为d φ。

潜艇所能承受的最大风倾力矩max f M（或力臂m ax f l）在静稳性曲线图上，如图1所示，如增大倾斜力矩f M ，则垂线CD 将向右移，当D 点达到下降段上的D ‘位置时,'''''D C B B OA S S =,如倾斜力矩f M 再增大,复原力矩所作的功不能与倾斜力矩所作的功相等，所以，这时的倾斜力矩即为所求的最大倾斜力矩max f M （或力臂m ax f l ），D ‘点相对应的倾角称为极限动横倾角m ax d φ。

船舶静力学考研真题

船舶静力学考研真题船舶静力学是船舶与水的力学相互作用的研究，是船舶工程领域中的重要分支。

本文将通过一道船舶静力学考研真题，来探讨船舶静力学的相关知识。

一、题目描述某船舶的重心高度为G=12m，初始浮心高度为B=14m，船体折割点偏心量为e=1.6m。

当此船停泊在一水深为H=20m的水上时，请计算此时船舶是否会发生侧翻。

二、问题分析在本题中，我们需要计算船舶是否会发生侧翻，即判断船舶的倾覆稳定性。

船舶的倾覆稳定性受到重力和浮力的相互作用影响，需要通过计算浮力和重力的力矩来判断。

三、计算过程1. 确定水面与船体折割点间的距离：h = H - e = 20m - 1.6m = 18.4m。

2. 计算重力矩：Mg = G * Tg，其中Tg为船舶总重力。

3. 计算浮力矩：Mf = B * Tf，其中Tf为船舶的浮力。

4. 判断船舶是否会发生侧翻：- 若Mf > Mg，则船舶不会发生侧翻，稳定。

- 若Mf <= Mg，则船舶会发生侧翻，不稳定。

四、计算结果1. 计算重力矩：- 船舶总重力Tg = m * g，其中m为船舶的质量，g为重力加速度。

- 假设船舶的质量为100吨，则m = 100 * 1000 kg。

根据题目中给出的重心高度G=12m，计算得到：- Mg = G * Tg = 12m * 100 * 1000 kg * 9.8 m/s^2。

2. 计算浮力矩：- 船舶的浮力Tf = V * ρ * g，其中V为船舶的体积，ρ为水的密度。

由于题目未给出具体船舶形状和尺寸，故无法准确计算船舶的体积。

因此，我们假设船舶的体积为1000立方米。

同时，水的密度ρ = 1000 kg/m^3。

根据题目中给出的初始浮心高度B=14m，计算得到：- Mf = B * Tf = 14m * 1000 m^3 * 1000 kg/m^3 * 9.8 m/s^2。

3. 判断船舶是否会发生侧翻：- 若Mf > Mg，则船舶不会发生侧翻，稳定。

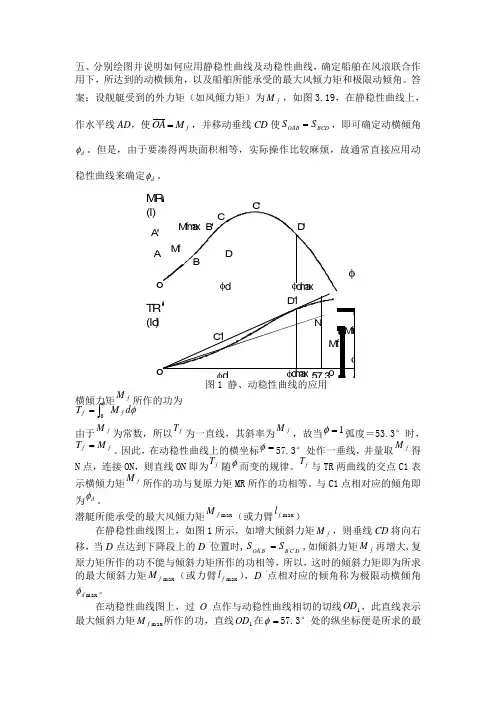
船舶静力学习题

五、分别绘图并说明如何应用静稳性曲线及动稳性曲线，确定船舶在风浪联合作用下，所达到的动横倾角，以及船舶所能承受的最大风倾力矩和极限动倾角。

答案：设舰艇受到的外力矩（如风倾力矩）为f M ，如图3.19，在静稳性曲线上，作水平线AD ，使f M OA =，并移动垂线CD 使BCD OAB S S =，即可确定动横倾角d φ。

但是，由于要凑得两块面积相等，实际操作比较麻烦，故通常直接应用动稳性曲线来确定d φ。

φM R (l)o BACφdoT R (ld )φM fDM fm a x φd57.3oM fM fm a xφd m a xφd m a x C 'A 'B 'D 'NC 1D 1图1 静、动稳性曲线的应用横倾力矩fM 所作的功为 φφd M T f f ⎰=0 由于f M 为常数，所以f T 为一直线，其斜率为f M，故当1=φ弧度＝53.3°时，ff M T =。

因此，在动稳性曲线上的横坐标=φ57.3°处作一垂线，并量取f M 得N 点，连接ON ，则直线ON 即为f T 随φ而变的规律。

f T与TR 两曲线的交点C1表示横倾力矩f M所作的功与复原力矩MR 所作的功相等。

与C1点相对应的倾角即为d φ。

潜艇所能承受的最大风倾力矩max f M （或力臂max f l）在静稳性曲线图上，如图1所示，如增大倾斜力矩f M ，则垂线CD 将向右移，当D 点达到下降段上的D ‘位置时,'''''D C B B O A S S =,如倾斜力矩f M 再增大,复原力矩所作的功不能与倾斜力矩所作的功相等，所以，这时的倾斜力矩即为所求的最大倾斜力矩max f M （或力臂max f l ），D ‘点相对应的倾角称为极限动横倾角max d φ。

在动稳性曲线图上，过O 点作与动稳性曲线相切的切线1OD ，此直线表示最大倾斜力矩max f M 所作的功，直线1OD 在=φ57.3°处的纵坐标便是所求的最大倾斜力矩max f M （或力臂max f l ），切点D 1对应的倾角便是极限动横倾角max d 。

华科船舶结构强度第二次大作业

船体强度与结构设计------第二次大作业班级：姓名：学号：题目：图示为某船舶横剖面结构示意图。

请计算当船舶船舯为波谷，且弯矩值为9.0×107N ·m ，考虑折减系数计算总纵弯矩应力。

解答：一、计算依据 1、计算载荷计算弯矩 79.010m M N =⨯⋅2、船体材料计算剖面的所有构件均采用低碳钢，屈服极限=235aY MP σ3、许用应力（1）总纵弯曲许用应力[]0.5Yσσ=(2)总纵弯曲与板架局部玩去合成应力的许用应力：在板架跨中 12[+]0.65Y σσσ= 在横仓壁处 12[+]Y σσσ=二、总纵弯曲正应力计算1、总纵弯曲正应力第一次近似计算肋骨剖面计算简图如题图所示。

将图中个强力构件编号并将其尺寸填入表中。

船体剖面要素及第一次近似总纵弯曲应力的计算在下表中完成。

在计算中，参考轴取在基线处。

利用上表中的数据可得第一次近似中和轴距参考轴的距离为：=2748.361702.81=1.614m ∆÷所以，第一次近似中和轴距基线的距离为1.614m 船体剖面对水平中和轴的惯性矩为：222=2(9951.42138.512748.361702.81)11308.1cm m I ⨯+-÷=⋅剖面上各构件的应力为：'i i =/100M Z Iσ 式中'i i Z Z =-∆ 2、临界压力计算由于该计算中船舶船舯处于波谷中，即船舶处于中垂状态，所以下面只列出中和轴以上部分受压板的临界应力。

纵骨架式板格（四边自由支持）按下式计算：210076()cr t bσ=3、船体总纵弯曲应力第二次近似计算（1）剖面折减系数计算已知本船体结构为纵骨架势，因此对于只参加抵抗总纵弯曲的构件criσϕβσ=式中 cr σ——板格的临界应力i σ——与所计算的板在同一水平线上的刚性构件总纵弯曲压应力的绝对值β——系数，275btβ=-，若1β>，则取1β= b ——纵骨间距计算结果见下表：（2）总纵弯曲应力第二次近似计算由上表知本船在波谷位置时，甲板板发生折减。

船舶静力学习题集

船舶静力学习题集《船舶静力学》习题集《船舶静力学》习题集严谨敬业办公勤学校训求实团结教风精业Ayen工作作风唯实勤勉学风勤思求真第一章绪论坚忍善育高效率力争上游第2页《船舶静力学》习题集自学目标1．了解课程学习内容2．掌控补足科学知识中的有关概念思考与练习1．船舶原理研究哪些内容？2．中机形船、尾机形船各有什么优缺点？3．船体坐标的正负是怎么规定的？第二章船体几何要素及船体近似计算法学习目标1.掌控船体主尺度、船型系数等船形参数的定义及几何意义；能根据有关数据排序船型系数。

2.船体几何要素包括船体主尺度、船形系数和尺度比,是表示船体大小、形状、肥瘦程度的几何参数。

3.认知船体近似计算法的基本原理；4.掌握梯形法、辛氏法的计算公式；运用梯形法、辛氏法进行积分的近似计算.5.掌握运用梯形法进行船体水线面和横剖面计算的数值积分公式及计算表格。

6.实例练习思索与练1.作图说明船体的主尺度是怎样定义的？其尺度比的主要物理意义如何？2．作图说明船形系数是怎样定义的?其物理意义如何?试举一例说明其间的关系。

3．某海洋客船船长l=155m,船宽b=18.0m,吃水d=7.1m排水体积?=10900m3。

中横剖面面积am=115m2,水线面面积aw=1980m2.试求:(1)方形系数cb;(2)横向棱形系数cp;(3)水线面系数cwp;(4)中横剖面系数cm;(5)橡胶垫棱形系败cvp。

4.两相等的正圆锥体在底部处相连接,每个锥体的高等于其底部直径.这个组合体浮于水面,使其两个顶点在水表面上试绘图并计算：(1)中横剖面系数cm;(2)横向棱形系数cp;(3)水线面系数cwp;(4)方形系数cb。

5.某游艇排洪体积?=25m3,主尺度比为：宽度比l/b=5.0,宽度排水量比b/d=2.7,方形系cb=0.52,谋：该艇的主要尺度l、b及d。

第3页《船舶静力学》习题集6.试说明船舶静力学计算中常用的近似计算法有哪几种?梯形法和辛氏法的基本原理以及它们的优缺点？7.设曲线方程为y=sinx,利用以下各种方法排序准确求解展开比较,并算出相对误差。

船舶静力学考试题及答案

船舶静力学考试题及答案一、单项选择题（每题2分，共20分）1. 船舶在静水中的浮态通常是指（）。

A. 正浮B. 半载C. 满载D. 空载答案：A2. 船舶的排水量是指（）。

A. 船体自重B. 船体和货物的总重量C. 船体排开水的质量D. 船体和货物的总体积答案：C3. 船舶的重心是指（）。

A. 船体重心B. 货物重心C. 船体和货物的共同重心D. 船体和货物的共同质心答案：D4. 船舶的稳心是指（）。

A. 浮心B. 重心C. 船舶正浮时的重心D. 船舶正浮时的浮心答案：D5. 船舶的初稳性高是指（）。

A. 重心到基线的距离B. 重心到浮心的距离C. 浮心到基线的距离D. 重心到浮心的距离答案：D6. 船舶的横倾角是指（）。

A. 船舶纵轴与水平面的夹角B. 船舶纵轴与垂直面的夹角C. 船舶横轴与水平面的夹角D. 船舶横轴与垂直面的夹角答案：C7. 船舶的横倾力矩是指（）。

A. 由于重力产生的力矩B. 由于浮力产生的力矩C. 由于重力和浮力产生的力矩D. 由于外力产生的力矩答案：D8. 船舶的横倾力臂是指（）。

A. 重心到浮心的距离B. 重心到基线的距离C. 浮心到基线的距离D. 重心到浮心的距离答案：A9. 船舶的横倾力矩平衡条件是（）。

A. 横倾力矩等于零B. 横倾力矩大于零C. 横倾力矩小于零D. 横倾力矩等于横倾力臂乘以重力答案：A10. 船舶的横倾回复力矩是指（）。

A. 由于重力产生的力矩B. 由于浮力产生的力矩C. 由于重力和浮力产生的力矩D. 由于外力产生的力矩答案：C二、多项选择题（每题3分，共15分）11. 船舶的浮性包括（）。

A. 正浮B. 半载C. 排水量D. 浮心位置答案：AC12. 船舶的稳性包括（）。

A. 初稳性B. 大倾角稳性C. 横倾力矩D. 横倾力臂答案：AB13. 影响船舶稳性的因素包括（）。

A. 船体形状B. 货物分布C. 船体材料D. 船舶载重答案：ABD14. 船舶的横倾可能由以下哪些因素引起（）。

2016-2018年华南理工大学814船舶静力学硕士研究生入学考试题

814
华南理工大学
2018年攻读硕士学位研究生入学考试试卷（试卷上做答无效，请在答题纸上做答，试后本卷必须与答题纸一同交回）
科目名称：船舶静力学
适用专业：船舶与海洋工程；船舶与海洋工程(专硕)
图1 半潜船艉浮箱
所示为两种典型的船舶静稳性曲线。

某方形浮码头
LxBxD=20x5x3(单位：m)。

请问它的静稳性曲线更接近于图中哪种情况，并阐释其特
图2 两种典型的船舶静稳性曲线
为瓦良格号航母的下水现场图片，试判断其下水方式。

图3置，试分析其用途。

图3 瓦良格号航母的下水现场
图4 静稳性力臂曲线和动稳性力臂曲线
图5方形浮码头主尺度
6方形浮码头横剖面浸湿
吃水为1.0m时的排水体积和浮心垂向坐标
排水体积V= m3
浮心垂向坐标zb= m
814
华南理工大学
2017年攻读硕士学位研究生入学考试试卷
（试卷上做答无效，请在答题纸上做答，试后本卷必须与答题纸一同交回）
科目名称：船舶静力学
适用专业：船舶与海洋工程；船舶与海洋工程（专硕）
814
华南理工大学
2016年攻读硕士学位研究生入学考试试卷
（试卷上做答无效，请在答题纸上做答，试后本卷必须与答题纸一同交回）
科目名称：船舶静力学
适用专业：船舶与海洋工程
（其中，的单位为；
=30。

船舶静力学作业

b=1.5m，l1=2m，l2=1.5m，b1=1.2m，b2=1.5m。求：该水线面面积 Aw 及形心坐标 XB、YB，。
2－3
某船水线长 L＝100m，在正浮状态时，各站号的横剖面面积如下表所列： 6 54.3 7 44.7 8 30.1 9 13.5 10 0
0 1 2 3 4 5 站号横剖面面 0 13.3 30.4 44.4 53.8 57.3 积（1）以适当比例画出该船的横剖面面积曲线；浮心纵向坐标 XB；（3）求纵向棱形系数 Cp。 2－4
z 4 3 2 1 0 2.24 1.00 1.00 1.00 1.00 2.00 1.60 1.20 z 6.00 4 3 2 1 y 0 5.16 4.10 2.25
1.00 1.00 1.00 1.00 y
1－12
某船的水线面曲线在各站号处的半宽值如下表所列（站距为 12m）站号 0 0 1 2 3 4 5 6 7 8 9 10 0 6.35 8.55 8.67 8.67 8.47 8.67 8.60 7.55 4.18
（2）用梯形法和辛氏第一法按表格计算排水体积 ∇ ，用梯形法和辛氏第一法按表格计算
某海船中横剖面是长方形。各水线长均为 128m，最大宽度为 15.2m，每隔 1.22m 自
上而下各水线面面积系数是；0.80，0.78，0.72，0.62,0.24 和 0.04。试列表计算：（1）各水线的每厘米吃水吨数；（2）最高水线下的排水量和浮心垂向坐标；（3）自上而下第二水线下的排水量和浮心垂向坐标；（4）最高水线下的方形系数；（5）最高水线下的棱形系数。 2－5 某船长为 60m ，其水线下横剖面为半圆形（其形心里向的位置距基线高为

船舶静力学试题

00船舶与海洋工程专业《船舶静力学》试题B姓名：学号：_______ 一、综合题（填空）（30分）1．梯形法计算公式为（⎥⎦⎤⎢⎣⎡-≈=A ∑⎰=n i i dy n L x y 00d ε），其中修正项是（ ε = 20n y y +）； 2．梯形法、高斯法、辛浦生法和乞贝雪夫法在纵坐标数目相同的情况下，计算精度由高到低依次为（高斯法）、(乞贝雪夫法)、(辛浦生法)、 (梯形法)；3．写出三心（浮心、重心和稳心的垂向坐标之间的关系，即稳性高GM 等于（GM=BM+KB-KG ）；4．LGM MTC L 100⋅∆=称为（引起纵倾1cm 的纵倾力矩），其中L 为（船长），∆为（排水量），GM L 为（纵稳性高）；5．船舶的平衡条件是（1）：（重力与浮力的大小相等方向相反）；（2）：（重心和浮心在同一条铅垂线上）；6．横剖面面积曲线是以（船长L ）为横坐标，以（横剖面面积A 0）为纵坐标所绘制的一条曲线，它与横轴所围成的面积表示（该吃水时的排水体积）的大小，它的形状表示（船舶排水体积）沿（船长方向）的分布；7．船舶的横稳心高与横稳性高是不同的概念，横稳性高表示的是（横稳心和重心）之间的距离，而横稳心高表示的是（横稳心和浮心）之间的距离；8．∇=T I BM 称为（初稳心半径），它表示的是（横稳心和浮心）两点之间的距离，其中I T 为（水线面积对于纵向中心轴线的横向惯性矩），∇为（排水体积）；9．排水量为∇的船上有一重量为p 的重物，重物的横向移动距离为l ，船的初稳性高为 GM ，船的横倾角正切tg φ为等于（GMΔl p ⨯⨯=φtg ）； 10．当船舶发生小角度横倾时，倾斜水线面与正浮时水线面相交于通过（原水线面漂心）的纵轴。

二、回答问题（40分）1．绘出静稳性曲线的示意图，并说明什么是动横倾角？什么是静横倾角？2．什么是稳性横截曲线？绘出曲线的示意图并标出和说明曲线的纵坐标和横坐标。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

表4：表4给出了用不同船型不同方法在低速阻力测试试验中得出的外形因子的汇总；从表中可以看出，无论是直接法还是间接法，除了较小尺寸的模型船都得到了较好的可以接受的结果，而用间接法可以得出一致性更好的结果。特别地，间接法更具有优势：得出的结果既不依赖于指数n也不依赖于多项式方程的形式。因此选择以下约定作为标准： » 直接法进行计算 » 取指数n=5 » 采用二次拟合
单击此处编辑母版标题样式理论研究
然而，在模型试验中，还有一种方法能够在保持傅汝德数相同的基础上改变雷诺数，即改变实船与模型船之间的缩尺比。将缩尺比记为λ ，则雷 1 诺数与 λ^ .5成正比。
4、模型试验
1）本研究中，共选了12种不同的船型，如下表1 所示；模型试验从1992年到2006年共进行了15年，如表2所示；
上式中，a是与波形阻力系数相关的常量；n代表波形阻力的大小，是个常量。从物理的角度看指数n一般在4-6 之间变化，其值取决于船型。在本次研究中分别用n=4、5、 6来研究不同的指数取值对实验结果的影响。
单击此处编辑母版标题样式理论研究
在间接法的计算中，用从低速船模试验中的数据 FnN/CFM和CTM/CFM对应，并为了应用方便，用如下符号进行替换：
单击此处编辑母版标题样式试验及分析
单击此处编辑母版标题样式试验及分析
单击此处编辑母版标题样式试验及分析
一般情况下，由于在速度十分接近设计速度的时测量出的阻力值是离散的，所以在设计速度下很难得出一致的有实际意义的形状因数。如表5 所示，然而，得到有实用价值的数据是完全有可以的。当得出在设计速度下的外形因数时，应当明白它是另外的流体动力学问题。与低速范围的情形形成对比，在设计速度下产生的船行波会影响到外形阻力，也即是说外形阻力受到雷诺数和傅汝德数的双重影响。然而没有方法去估计雷诺数、傅汝德数和用目前的研究结果的得出的外形因子之间的相互关系。
单击此处编辑母版标题样式试验及分析
Table1
单击此处编辑母版标题样式试验及分析
Table2
单击此处编辑母版标题样式试验及分析
2）为了系统地分析试验结果，把选中的12种船型分为4 组：the fine higher-speed ship group, the gas carrier group, the full slow-speed ship group, and the special ship group;如下表所示：
单击此处编辑母版标题样式研究方向
所以研究ITTC提出的外形因子概念的有效性是非常有必要的。因此作者进行了以下三个基本研究：（1）依据ITTC的定义求解船舶外形系数的方法（2）船舶外形因子与雷诺数之间的关系（3）在给定航速时求解船舶外形系数的方法所有基本的和必须的试验都是在HMRI（现代重工海事研究所）的深水池中进行。试验水池长220m,宽14m,深6m。一些特殊的测试在汉堡船模试验水池（HSVA）和瑞典的SSPA进行。在本文中，作者仅给出了在HMRL试验中得出的数据与试验结果。
然后用最小二乘法对上式分别进行二次拟合和三次拟合，即可将外形因子表示成常量形式。
单击此处编辑母版标题样式理论研究
2、关于在设计航速下外形因子计算的建议
当雷诺数大于107时流体可以看成全部处于紊流状态，此时的外形因子无限接近一个常量。因此试验要尽可能在雷诺数大于107的速度下进行。幸运的是作者发现当模型船的长度大于6m且当其速度与实船的设计速度相对应时，这种情况就更令人满意。下面关于波形阻力系数的表达式是在当模型速度与设计速度保持很小差别时外形因子几乎保持为常量的假设的基础上引入的：
单击此处编辑母版标题样式研究方向
汉堡船模试验水池（HSVA） HSVA home page： /valanto.htm SSPA简介：SSPA海事齐询公司设于CHARLMER理工大学校园内。CHARLMER是瑞典著名的工学院，尤其是船舶工程。冷战时期这里是绝密之地，至今仍保留着一套安全体系。然而，更优秀的是发达的软件业即计算机辅助设计及电脑模拟。 SSPA home page：http://www.sspa.se/home
5.实验结果及分析 5.实验结果及分析
1）.低速阻力测试实验与外形因子的计算如前面提到的，为了求取外形因子，对选定的32条模型船反复地进行低速阻力测试试验。下面图4、5、6展示了依据ITTC定义推出的外形因子随傅汝德数变化的趋势：
图4：小尺寸模型船的阻力变化趋势与大尺寸的变化不同，这种现象在试验中相当常见。因为在这一系列试验中雷诺数约为10^5，此时船模周围的流体为层流或者过渡状态。
Fig. 3 Models of the 317,000-TDW very large crude carrier (VLCC)
Fig. 2 Models of the 155,000-m3 liquefied natural gas (LNG) carrier
单击此处编辑母版标题样式试验及分析
单击此处编辑母版标题样式试验及分析
单击此处编辑母版标题样式试验及分析
单击此处编辑母版标题样式试验及分析
单击此处编辑母版标题样式试验及分析
Table 4 Sample form factors determined from low-speed resistance tests
单击此处编辑母版标题样式试验及分析
单击此处编辑母版标题样式理论研究
为此，作者尝试提出一种依据ITTC定义来计算船舶外形因子的通用方法。 2）.直接法（1）数据选取。对于CTM/CFM的值来说需要极小的傅汝德数，这就要求进行较低速的阻力测试。为了使用方便进行如下代换： x=FN, y=CTM/CFM (6) 利用最小二乘法将数据拟合成下面的多项式等式曲线：
在该理论中，利用ITTC'57曲线计算摩擦阻力系数：
上式中，RN为雷诺数，V为船舶航行速度，L为船长，为运动粘性系数 υ
单击此处编辑母版标题样式 ITTC'78简介简介
单击此处编辑母版标题样式 ITTC'78简介 ITTC'78简介
尽管这个方法已经被ITTC所采取并作为标准计算方法，然而依据该理论进行的实船阻力性能预测的结果却随着模型试验水池的变化而变化，这已是业内专家所熟知现象。这种现象的发生可能是由两个原因造成：一是外形因子的确定，首先在低速情况下测量阻力是十分困难的，所以根据外形因子的定义准确地得出外形因数是十分困难的；二是两个基本假设本身的准确性。但事实上，作者也支持外形因子这个概念。该作者认为无论在何种情况下，能够分别出与船体外形有பைடு நூலகம்的阻力成分都是具有实际意义的。
单击此处编辑母版标题样式试验及分析
3）为了求取外形因子，依据ITTC定义，对 32条模型船全部进行低速阻力测试试验；对12条条模型船在速度接近设计航速时进行阻力测试试验。下列图标分别给出了四种模型船及相应的不同尺寸的模型：
单击此处编辑母版标题样式试验及分析
Fig. 1 Models of the 8,600-TEU container carrier
单击此处编辑母版标题样式理论研究
利用大型的模型船进行试验，在几个与设计速度相差极小的速度下便可分别测出其对应的阻力值，再将在两个相邻的速度上获得的阻力值带入上述方程组便可解出外形因子和波形阻力因子。
单击此处编辑母版标题样式理论研究
3、外形因子与雷诺数之间的联系
1）说明：随着船舶速度的增大，产生的船行波对外形阻力的影响便不断增强，也就是外形因子开始受傅汝德数与雷诺数的双重影响。如果要研究船行波对外形阻力的影响，还需要再一系列基本的研究。为了本研究的进展，船行波对外形的影响已经被排除，即假设外形阻力仅与雷诺数有关。 2）研究理论为了研究外形因子与雷诺数之间的关系，外形因子的测量应该在不同的雷诺数下进行。试验中如果保持一定的实模比，应通过增大拖拽速度而使雷诺数增加，但如此一来便不能够采用ITTC的定义来计算外形因子了。
单击此处编辑母版标题样式理论研究
1、利用ITTC定义计算外形因子的建议利用ITTC定义计算外形因子的建议 ITTC
1）.概要模型船的总阻力系数表述如下： CTM=(1+k)CFM+CW （5）如果能够同步地测量出模型船的总阻力和波形阻力，那么利用式（5）便可求得较精确的外形因子。然而，由于测量波形阻力不仅困难而且误差也很大，所以这种方法并没有实际意义。此外，利用定义（2）直接计算外形因子也是不可能的。而在实际应用中，通常通过测量模型船低速运动的阻力来间接求取外形因子，可问题是准确地测量模型船的低速阻力是很困难的。
单击此处编辑母版标题样式试验及分析
2）.在速度接近设计速度时的阻力测试和外形因子的计算回顾前面所述的计算方法：
在等式13中取用不同的指数n 在等式13中，取用不同的指数n，既n=6，参数选 13 n=6，取的依据是不同速度范围的波浪阻力理论。取的依据是不同速度范围的波浪阻力理论。所有为求取外形因子而进行的低速阻力试验和速度接近设计速度的模型试验结果均被汇集在表5 近设计速度的模型试验结果均被汇集在表5中。
考虑到船体外形主尺度对船舶阻力的影响，考虑到船体外形主尺度对船舶阻力的影响，1978 年国际拖曳水池会议（ITTC）年国际拖曳水池会议（ITTC）通过了船舶阻力测试方法，在两个基本假设的基础上引入了外形因试方法，子的概念。两个基本假设为：子的概念。两个基本假设为： 1）模型船的外形因子与实船相同 2）外形因子与船舶航行速度无关然而，依据ITTC'78定义的方法不仅很难确定外 ITTC'78定义然而，依据ITTC'78定义的方法不仅很难确定外形因子，形因子，而且两个基本假设本身也有许多无法解决的问题，决的问题，为此作者进行了三次关于船体外形因子的基本研究，子的基本研究，为实船的阻力性能计算提出了一个新的理论。个新的理论。