智慧金字塔立体篇第四册、第五册答案全解
- 格式:doc
- 大小:6.20 MB
- 文档页数:60

第一单元 生活智慧与时代精神政治·必修4·人教版一、选择题:本题共20小题,每小题3分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
黑格尔是德国古典哲学著名代表,其对哲学做出过许多非常形象生动而又耐人寻味的比喻,引人深思。
回答1—2题。
1.黑格尔曾经说过哲学是人的精神的故乡,“一个有文化的民族”,如果没有哲学,“就像一座庙,其他各方面都装饰得富丽堂皇,却没有至圣的神那样”。
这是因为( )①哲学是给人智慧、使人聪明的学问②哲学智慧产生于人类的实践活动③真正的哲学为生活和实践提供积极有益的指导④哲学是科学的世界观和方法论A.①②B.①③C.②④D.③④2.针对有人将哲学看得太容易,不致力于哲学研究却高谈阔论,还装作非常内行的样子,黑格尔打过一个比方:人人有脚作模型,也有学习制鞋的天赋,但做鞋必须有专门的技术,否则不敢妄事制作。
这告诉我们( )①自觉学习和研究哲学是非常必要的②世界观人人都有,但并非人人都是哲学家③学习了哲学就等于掌握了一门专门技能④掌握专门技术才有资本就哲学高谈阔论A.①②B.①③C.②④D.③④1.B 【解题思路】 材料强调的是要发挥哲学的作用,①③分别从本质和作用上正确指出了其中的原因。
②与题干不构成因果关系。
哲学不都是科学的世界观和方法论,④说法错误。
2.A 【解题思路】 人人有脚作模型,也有学习制鞋的天赋,但做鞋必须有专门的技术,否则不敢妄事制作,这形象地说明,世界观人人都有,但一般人自发形成的世界观还不等于哲学,只有哲学家依据一定的自然知识、社会知识和思维知识,把不自觉、不系统的世界观加以系统化、理论化而形成思想体系才能产生哲学,也说明自觉学习和研究哲学是非常必要的,①②符合题意。
③④明显错误。
3.[2019江苏扬州中学阶段性检测]下列看法中,属于世界观的有( )①物质是不依赖于人的意识并能为人的意识所反映的客观实在 ②一切从实际出发 ③水往低处流 ④存在即被感知 ⑤天行有常,不为尧存,不为桀亡A.①②④⑤B.①②③④⑤C.①②⑤D.①④⑤3.D 【解题思路】 世界观是人们对整个世界的总的看法和根本观点,①④⑤入选。
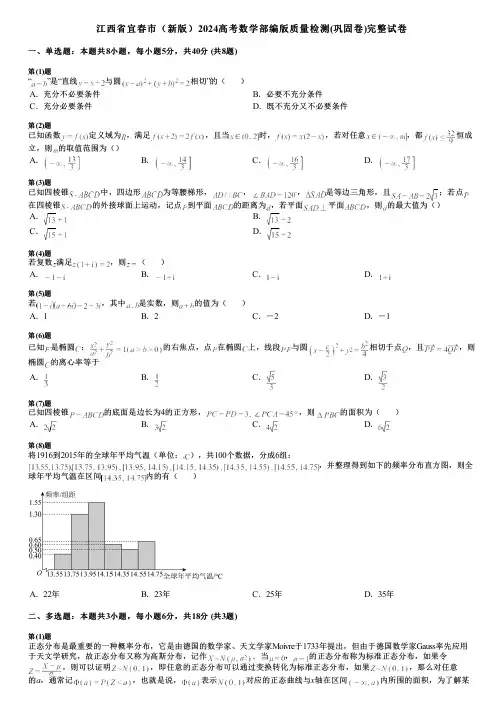
江西省宜春市(新版)2024高考数学部编版质量检测(巩固卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题“”是“直线与圆相切”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件第(2)题已知函数定义域为,满足,且当时,,若对任意,都恒成立,则的取值范围为()A.B.C.D.第(3)题已知四棱锥中,四边形为等腰梯形,,,是等边三角形,且;若点在四棱锥的外接球面上运动,记点到平面的距离为,若平面平面,则的最大值为()A.B.C.D.第(4)题若复数满足,则()A.B.C.D.第(5)题若,其中是实数,则的值为()A.1B.2C.-2D.-1第(6)题已知是椭圆:的右焦点,点在椭圆上,线段与圆相切于点,且,则椭圆的离心率等于A.B.C.D.第(7)题已知四棱锥的底面是边长为4的正方形,,则的面积为()A.B.C.D.第(8)题将1916到2015年的全球年平均气温(单位:),共100个数据,分成6组:,并整理得到如下的频率分布直方图,则全球年平均气温在区间内的有()A.22年B.23年C.25年D.35年二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题正态分布是最重要的一种概率分布,它是由德国的数学家、天文学家Moivre于1733年提出,但由于德国数学家Gauss率先应用于天文学研究,故正态分布又称为高斯分布,记作.当,的正态分布称为标准正态分布,如果令,则可以证明,即任意的正态分布可以通过变换转化为标准正态分布,如果,那么对任意的a,通常记,也就是说,表示对应的正态曲线与x轴在区间内所围的面积,为了解某市高三数学复习备考情况,该市教研机构组织了一次模拟考试、研究发现,本次检测的数学成绩X近似服从正态分布.则下列说法正确的有()参考数据:可供查询的(部分)标准正态分布对应的概率值.a0.240.250.260.350.360.59480.59870.60640.63680.6406A.已知,则B.C.按以往的统计数据,该市数学成绩能达到升一本分数要求的同学约占,据此估计本次检测成绩达到升一本的数学成绩约为108(精确到整数)D.已知该市考生约有10000名,某学生此次检测数学成绩为110分,则该学生在全市排名大概位于名之间第(2)题下列说法中正确的是()A.用简单随机抽样的方法从含有60个个体的总体中抽取一个容量为6的样本,则个体m被抽到的概率是0.1B.已知一组数据1,2,m,6,7的平均数为4,则这组数据的方差是C.数据13,27,24,12,14,30,15,17,19,23的第70百分位数是23D.若样本数据的标准差为8,则数据的标准差为32第(3)题下列物体中,能够被整体放入棱长为1(单位:)的正方体容器(容器壁厚度忽略不计)内的有()A.表面积为的球体B.体积为的正四面体C.体积为的圆柱体D.底面直径为,高为的圆锥三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知抛物线:的焦点为,过且斜率为1的直线交于,两点,若的面积为,则______.第(2)题若复数满足,其中是虚数单位,则___________.第(3)题如图,在正四棱台中,上、下底面的棱长分别为2和3,侧棱长为,分别延长,,,交于点,则四棱锥的体积为______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题2021年春晚首次采用“云”传播、“云”互动形式,实现隔空连线心意相通,春晚还将现场观众互动和“云观众”融入现场,全球华人心连心“云团圆”,共享新春氛围.“云课堂”亦是一种真正完全突破时空限制的全方位互动性学习模式,某市随机抽取200人对“云课堂”倡议的了解情况进行了问卷调查,统计结果如下表所示:了解情况了解不了解人数14060(1)请根据所提供的数据,完成下面的列联表,并判断能否有99%的把握认为是否了解“云课堂”倡议与性别有关;男女合计了解80不了解40合计(2)用样本估计总体,将频率视为概率,在男性市民和女性市民中各随机抽取3人,记“3名男性中至少有1人了解云课堂倡议”的概率为,“3名女性中至少有1人了解云课堂倡议”的概率为,试求出与.附:,其中.0.100.050.0250.0100.0050.0012.7063.841 5.024 6.6357.87910.828第(2)题整数,集合,A,B,C是集合P的3个非空子集,记,为所有满足 ,的有序集合对的个数.(1)求;(2)求.第(3)题设数列是首项为1,公差为d的等差数列,且,,是等比数列的前三项.(1)求的通项公式;(2)设,求数列的前n项和.第(4)题如图2,在三棱锥中,为的中点.(1)证明:平面;(2)若点在上且,求点到平面的距离.第(5)题在中,内角的对边分别为.(1)判断的形状,并证明;(2)求的最小值.。

1、观潮温故知新一、略二、mèn zhàng bèn hùdiàn hào三、山崩地裂漫天卷地七上八下若隐若现风号浪吼东奔西走互为近义词的有:山崩地裂漫天卷地若隐若现风号浪吼互为反义词的有:七上八下东奔西走四、1✔ 2✔ 5✔五、1人山人海 2天下奇观 3人声鼎沸 4若隐若现六、1一次一回 2宽广 3依然仍然 4犹如 5一时6许久七、风平浪静一条白线犹如千万匹白色战马齐头并进,浩浩荡荡地飞奔而来;如同山崩地裂,好像大地都被震得颤动起来。
依旧风号浪吼江水已经涨了两丈来高了天下奇观惊叹自豪熟读精思1(霎)时间:瞬间,极短的时间。
无影无(踪):痕迹,脚印。
2.太阳的光更柔弱了,可它的脸颊更红了,像个大红球。
艳丽的晚霞弥漫了大半个天,像铺开了一幅巨大的瑰丽的绸缎。
3、时间动态颜色害羞的小姑娘大火球巨大的瑰丽的绸缎4、白日依山尽,黄河入海流——王之涣《登鹳雀楼》大漠孤烟直,长河落日圆。
——王维《使至塞上》落霞与孤鹜齐飞,秋水共长天一色。
——王勃《滕王阁序》山气日夕佳,飞鸟相与还。
——陶渊明《饮酒》一溪绿水皆春雨,半岸清山半夕阳。
——查慎行《池河驿》言为心声(略)【根据自己的想法来写】2 走月亮温故知新一、(略)二、葡萄庄稼跳跃风俗牵手鹅卵石三、高高的点苍山闪闪烁烁的小星星细细的溪水灰白色的鹅卵石秋虫唱着歌夜鸟拍打翅膀照亮大道运载新鲜的花瓣四、淘洗掏出风俗富裕兔子免礼五、明亮的月亮柔和的月亮美丽的月亮秋天的夜晚洒满湖光的夜晚奇妙的夜晚六、1明亮柔和 2洒满 3运载熟读精思(一)课内阅读1、月光闪闪月影团团美丽闪闪烁烁2、抒发了我和阿妈走月亮时无比幸福和喜悦的心情。
3、我的心完全陶醉在如梦似幻的意境中,天上人间,月亮、星星与阿妈和我已融为一体。
3、(写一个排比句)(二)课外阅读1、格外:分外,超出寻常。
微细:细微,细小。
2、每一种月光下的事物都有了光明,难道不是真好吗?(改成反问句)哪里都谈不上永恒之美。

新疆博尔塔拉蒙古自治州2024-2025学年四上数学第五单元《平行四边形和梯形》部编版基础掌握测试卷学校:_______ 班级:__________姓名:_______ 考号:__________(考试分数:100分时间:90分钟)注意事项:1.答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.所有题目必须在答题卡上作答,在试卷上作答无效。
3.考试结束后将试卷和答题卡一并交回。
总分栏题号一二三四五六七总分得分评卷人得分一、选择题(共16分)1.小红在一张纸上画了两条直线,分别用a、b表示,这两条直线的位置关系是a∥b。
小红画的是()。
A.B.C.D.2.看图选择.下面的直线,哪组是平行线?()A.B.C.D.3.下面说法中,错误的是()。
A.正方形相邻的两条边互相垂直。
B.两条直线互相平行,这两条直线相等。
C.长方形是特殊的平行四边形。
D.将圆平均分成360份,人们把其中的1份所对的角作为角的单位。
4.下面说法中,()不符合等腰梯形的特征。
A.两腰相等B.两腰平行C.两底角相等5.在同一个平面内,如果直线a和直线b分别与直线c互相垂直,那么直线a和直线b的位置关系是()。
A.互相平行B.互相垂直C.无法确定6.下面说法正确的是()。
A.每两个计数单位之间的进率是10。
B.直线比射线长。
C.只有一组对边平行的四边形叫做梯形。
7.丽丽在作业本上画了两条直线,这两条直线的位置关系是()。
A.相交或平行B.垂直或平行C.平行8.观察一下照片,你知道以下的测量运用了什么原理吗()A.点到直线的距离最短B.平行线间距离处处相等C.点到线的距离垂线段最短评卷人得分二、填空题(共16分)1.图中有________个平行四边形,________个梯形。
2.看一看,数一数.( )个长方形,( )个梯形,( )个平行四边形,( )个三角形3.标出下面图形的各部分名称.4.按要求填空:(1)写出不等式x<4的所有正整数解: .(2)写出不等式x≥﹣3的所有负整数解: .(3)写出不等式x≤3的所有非负整数解: .(4)写出不等式x>﹣2的最小整数解: .5.下面几组直线中,互相平行的有( ),互相垂直的有( )。

第十三讲沙漏与金字塔- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -观察故事中的第4幅图,太阳照下来在桌面上形成一个圆形的亮斑,如图1所示,我们将图形抽象成三角形,如图2所示.观察一下,这个图形与生活中的什么东西比较像?对了,沙漏!今天,就让我们来学习一下有关“沙漏”的知识.沙漏有一个必要条件:线段AB 平行于线段CD ,如图2所示.在沙漏中,我们总结出了如下性质:这就是我们今天要研究的平行线间的比例关系——即沙漏形三角形间的比例关系,简称沙漏.例题1.如图所示,梯形ABCD 的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少? 分析:图中给出的是一个梯形,梯形的上底和下底是平行的,你能找到平行线间的沙漏吗?如何利用这个沙漏呢?练习1.如图所示,梯形的面积是48平方厘米,下底是上底的3倍,求阴影部分的面积.图2A C图1A BC- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -在沙漏模型中,各线段的长度有比例关系,各区域的面积也有比例关系.如图所示,如果沙漏形的上下底之比为a :b ,四个三角形的面积之比为a ²:ab :ab :b ².- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题2.如图,平行四边形ABCD 的面积是90.已知E 点是AB 上靠近A 点的三等分点,求阴影部分的面积.分析:图中有没有沙漏形?它的上底与下底之比是多少? 练习2.如图,正方形ABCD 的边长是6,E 点是BC 的中点.求△AOD 的面积.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -寻找沙漏的时候,一定把握住一点:平行线.题目中如果出现了平行线,那么只要找到平行线间的相交线就可以找到沙漏.同学们在做题的过程中一定要用心体会这一点.小故事沙漏沙漏也叫做沙钟,是一种测量时间的装置.西方沙漏由两个玻璃球和一个狭窄的连接管道组成.利用上面的玻璃球的沙子穿过狭窄管道流入底部玻璃球所花费的时间来对时间进行测量.一旦所有的沙子都已流到底部玻璃球,该沙漏就可ABCD EOABCD EO以被颠倒以重新测量时间了.一般的沙漏有一个名义上的运行时间1小时.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题3.如图所示,边长为8厘米和12厘米的两个正方形并排放在一起,求图中阴影部分的面积. 分析:图中有很多组平行线,那么这些平行线就构造出很多沙漏,你能找出这些沙漏吗?那么想求阴影部分的面积,该利用哪一个沙漏呢?练习3.如图所示,图中的两个正方形的边长分别是10和6,那么阴影部分的面积是多少?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -我们发现,沙漏模型由一组平行线和一组相交线构成,且相交线的交点在平行线之间.如果交点在两条平行线的同一侧,就会构成一种新的模型,我们形象的称之为金字塔模型.在金字塔模型中也有相应的比例关系.111222a b c a b c == 1122a b a b = 11112122a b ca ab bc ==++ 沙漏模型金字塔模型FB- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4.如图,直角三角形ABC 中,AB =4,BC =6.又知BE :EC =1:3,求△CDE 的面积.练习4.如图,EF 与BC 平行,:1:2AF FB =.已知2AE =,3EF =,那么CE 的长度是多少?AC 的长度是多少?BC 的长度是多少?例题5.如图所示,在正方形ABCD 中,E 、F 分别是BC 、CD 的中点,已知正方形ABCD 的面积为60平方厘米,求阴影部分的面积.分析:如图所示,假设阴影三角形的另外两个顶点是G 和H .容易看出,三角形AGH 在三角形ABD 中,而三角形ABD 的面积是正方形ABCD 的一半,如果我们能够找到这两个三角形之间的面积关系,那么本题也就迎刃而解了.AFEBCD F例题6.已知三角形ADE的面积为3平方厘米,D是AB边的三等分点(靠近A点),且DE与BC平行,请求出三角形OBC的面积为多少平方厘米?分析:图中既有沙漏形,也有金字塔形.沙漏形的上底和下底分别是DE和BC,它们的比是多少?是不是需要用到金字塔形中的比例关系?AD EB OC埃及金字塔在非洲古国埃及的尼罗河畔,开罗城近郊的广裹沙漠中,巍然耸立着一群巨大的方锥形建筑物,这就是全球著名的古代世界八大奇观之首的埃及金字塔.它气势威严,历经沧桑,迄今已有四、五千年的历史.它又是古埃及高度文明的象征,是人类遥远历史的见证.金字塔以其形体极似汉字的“金”字,因此在中国称为“金字塔”.在欧洲则称为“庇拉米斯”,是古埃及语“高”的意思,可见高大是金字塔的特征.埃及金字塔是奴隶制帝王的陵墓,国王生前穷奢极欲,死后也仍想主宰天下.因此,在生前就不惜一切为自己修造所谓的“永久坚固的寓所”——金字塔,帝王希图永远保存自己的尸骨和尊严,于是从埃及第三王朝起便开始兴建金字塔.约在公元前2800-2300年之间,那是金字塔盛行的时代.在埃及有大、小金字塔70余座.第1座是埃及第三王朝国王杰赛尔的阶梯形金字塔,后来的角锥形金字塔,是在此基础上发展演变而来的.其中位于开罗郊区吉萨城附近的胡夫和哈夫拉两座金字塔,被列为世界古代八大奇观之首.这两座金字塔加上显示国王威严的狮身人面像,成为埃及金字塔风光的象征.胡夫金字塔规模最大,所以又称为“大金字塔”.它高146.5米,像一座40层高楼,拔地而起.在1889年巴黎埃菲尔铁塔(312.5米)修建之前,一直是世界上最高的建筑物.该塔占地80亩,边长2300多米,周长约1公里.全塔用230多万块大、小不同的巨石砌成,总体积250万立方米.平均每块石头重2.5吨,最重的一块约160吨.石块连接没有使用丝毫粘着物,但石块间丝隙皆无,使人赞叹!塔内有甫道、石阶、通风道和墓室.墓室分3层,位于塔底正中地下30米深处.胡夫大金字塔建筑之奇,至今仍是不解之谜.金字塔这样宏伟的建筑,有人认为是天外来客所建,但毕竟金字塔巍峨壮观地坐落在地球上,成为人类史上一座不朽的丰碑.它生动具体地告诉人们:古代埃及的奴隶们是怎样地在没有火药、没有机械的年代,利用双手及简单工具而创造出这一惊人的奇迹.金字塔至今作为世界奇观,傲对碧空,成为当今闻名世界的旅游胜地.作业1. 如图所示,DE 与BC平行,已知,,,则BC 的长度是多少?作业2. 如图所示,DE 与BC 平行,已知,,△ADE 的面积为32,则四边形DECB 面积是多少?作业3. 如图所示,梯形ABCD 的面积是50,下底长是上底长的1.5倍,阴影三角形的面积是多少?作业4. 如图所示,正方形ABCD 的边长是6,E 点是BC 的三等分点.△AOD 的面积是多少?作业5. 如图,平行四边形ABCD 的面积是12AC 与BE 的交点为F ,那么图中阴影部分面积是多少?5BD = 4AD = 16DE = 5BD = 4AD = ADE BCCADEBABCDBCE第十三讲 沙漏与金字塔例题1. 答案:16详解:上底与下底的长度比为1:2,设△OCD 面积是1份,则△AOD 与△BOC 的面积均为2份,△ABO 的面积为4份,共有9份,梯形面积为36,故一份所对应的面积为4.则△ABO 的面积为16.例题2. 答案:33详解:由沙漏模型知,:::2:3BE CD BO OD EO OC ===,设△OBE 的面积为4份,则△OBC 的面积为6份,△OCD 的面积为9份,△OBC 的面积与△OCD 的面积之和为整个四边形面积的一半,因此四边形的面积为30份,总面积为90,则一份对应的面积为3,阴影部分占了11份,面积为33.例题3. 答案:45详解:由条件知,:12:203:5GF BE ==,由沙漏模型知:3:5GO OE =,那么△GOF 与△EOF 的面积之比也是3:5.△OEF 的面积为512122458⨯÷⨯=.例题4. 答案:6.75详解:由金字塔模型知,::3:4DE AB CE CB ==,则3434DE =⨯=.又知道36 4.54CE =⨯=,可求出△CDE 的面积为3 4.52 6.75⨯÷=.例题5. 答案:10平方厘米详解:由条件知,1:2BE AD ==,则:1:2BG GD =,13BG BD =.同理,:1:2DF AB =,则:1:2DH HB =,13DH BD =.由此可得,13GH BD =.阴影部分面积为602310÷÷=平方厘米.例题6. 答案:13.5详解:由金字塔模型知,::1:3AD AB DE BC ==,设△ODE 的面积为1份,则△ODB 的面积为3份,△OEC 的面积为3份,△OBC 的面积为9份.又因为△ADE 与△DEC 等高,可知△ADE 的面积为2份,由此可知△OBC 的面积为32913.5÷⨯=平方厘米. 练习1.答案:27平方厘米简答:上底与下底之比为1:3.由沙漏模型可知四个三角形的面积之比是1:3:3:9,那么阴影部分的面积是()481339927÷+++⨯=平方厘米. 练习2.答案:12简答:连结DE ,因为BE 与AD 之比是1:2,可如图所示设份数.可知△AOD 的面积是正方形面积的三分之一,是12.BC E练习3.答案:400 13简答:58AH ADHG BG==,那么△ABH与△BGH的面积之比也是5:8,△ABH的面积是△ABG面积的5 13.5400 101621313⨯÷⨯=.练习4.答案:简答:12AF AEFB EC==,可求出4CE=,6AC=.13EF AFBC AB==,可求出9BC=.作业1.答案:36.简答:由金字塔模型,::4:9AD AB DE BC==,16DE=,则36BC=.作业2.答案:130.简答::4:9AD AB=,则:4:9AE AC=,△ADE是△ABC面积的1681,则△ABC的面积为162,四边形DEBC的面积为130.作业3.答案:18.简答:上底与下底的长度比为2:3,设△OCD面积是4份,则△AOD与△BOC的面积均为6份,△ABO的面积为9份,总面积为50,故一份所对应的面积为2.则△ABO的面积为18.作业4.答案:13.5.简答:由沙漏模型,::1:3BE AD BO OD==,△AOB与△AOD等高,面积比为1:3,因此△AOD的面积为3 66213.54⨯÷⨯=.作业5.答案:8.简答:AE:BC=2:3,设份数可知ABCD为30份,△AEF为4份,阴影部分占11份,面积为4.4.。


城关一小《教师教学智慧》作业冯文龙第一章理解教材的能力2012.11.261、理解教材指的是什么?答:一般所说的理解教材,主要指对教材中有关事物的本质和规律的认识,从而达到理性上的掌握。
理解教材主要包括璐姐教材的结构、教材的重点和难点、课文的编写思路、教材的优点和缺点。
第二章驾驭教材的能力2013.04.01一、驾驭教材的能力是指什么?答:驾驭教材的能力是指教师运用教材实施教学活动,并通过对教材的熟悉、研究、运用达到最理想化的教学效果的能力。
二、在驾驭教材的时候应从哪些地方入手?答: 1)、教师要树立正确的教材观。
2)、创造性地使用教材。
3)、采用合理的教学方法。
4)、恰当处理教学内容。
三、对于处理教材方面能力有欠缺的教师的几项建议?答:1)、适当调整顺序。
2)、适当删减内容3)、注重内在联系。
教师必须更新观念,充分调动自身的智慧与能力,这样才能不断提高处理教材的能力,为推动课堂教学的改革,实现教学创新二作出贡献,才能进行有效的教学活动,教给学生真正有用的知识。
第三章信息收集和处理的能力2013.06.10一、信息收集和处理的原则?答:1、准确性原则:该原则要求收集到的信息要真是、可靠。
2、全面性原则:给原则要求收集到的信息要广泛、全面完整。
3、时效性原则:信息的利用价值取决于该信息是否能及时的提供,即它的时效性。
4、可靠性原则:收集的信息必须是真实对象或环境产生的,必须保证收集的信息来源可靠,必须保证收集的信息能反映真实的状况。
二、教师如何具备大量但不加筛选信息的能力?答:1、教师应先培养自己适应网络阅读的能力,要能够从文本阅读走向超文本阅读;从单纯阅读文字发展到多媒体电子阅读;再到网络的高效率检索式阅读。
2、习惯用计算机写作包括掌握超文本结构的多媒体写作。
如:教学课件、个人网站建立等。
3、教师应学会和主动地在多媒体室或计算机室上课,边学边用,逐步掌握和提高应用能力。
4、教师应经常培养自己多用计算机处理日常食物的能力。

第一单元探索世界与把握规律第一课时代精神的精华第一框追求智慧的学问基础过关练题组一哲学的起源1.(2020广东深圳长江中学高二期中,改编)截至2019年8月12日5时50分,山东省受第9号台风“利奇马”影响,灾情涉及济南、青岛、淄博、枣庄、东营等14个市79个县(市、区)的522个乡镇(街道)。
对此,人们思考了一系列带有哲学性质的问题:人们能否提前发出准确预警?人们如何把灾害导致的损失降至最低?这表明()A.真正的哲学可以使我们正确地看待自然B.哲学智慧产生于人类的实践活动C.在实践中产生的思想都是哲学思想D.开展实践活动是为了适应哲学发展的需要2.(2020重庆一中高二月考,改编)朱熹小时候就问父亲“天上有何物”;陆九渊三四岁时就问父亲“天地有没有尽头”,并为此废寝忘食;波普尔八岁时就在思考“空间是无限的还是有限的”。
这些人后来成为大思想家与他们从小善于思考不无关系。
这说明(易错)A.哲学源于人们对自然万物的惊讶、困惑B.哲学思想源于伟大哲学家的智慧C.哲学起源于人们在生活实践中对宇宙、人生的追问和思考D.学习哲学是为了质疑现存的东西题组二哲学是系统化理论化的世界观3.(2020河南豫南九校联盟高二联考)世界观和方法论是同一问题的两个方面。
人们关于世界是什么、怎么样的根本观点是世界观,用这种观点去认识世界和改造世界,就成了方法论。
下列对世界观和方法论理解正确的是(易错)A.世界观和方法论不能相互脱离B.世界观和方法论就是哲学C.世界观和方法论密不可分、互为前提D.有什么样的方法论,就有什么样的世界观4.(2020福建泉州南安一中高二上月考,改编)心理学上有一种“自我实现的预言”的说法:当你为未知的未来许下一个预言,因为你相信事情会向预料的情况发展,所以你采取了加强的措施,这就提高了这个预言实现的可能性,最后的结果会同你自己的预言一样呈现在你眼前。
这种观点体现了()A.世界观决定方法论B.方法论影响世界观C.哲学是系统化理论化的世界观D.方法论决定世界观5.(2020黑龙江哈尔滨第三中学高二期末)中华文化崇尚和谐,中国“和”文化源远流长,蕴涵着天人合一的宇宙观、协和万邦的国际观、和而不同的社会观、人心和善的道德观。


智学智练同步达优高中语文必修五答案1、1《将进酒》这首诗的主旨句是“天生我材必有用,千金散尽还复来”。
[判断题] *对(正确答案)错2、1《项链》的作者是莫泊桑,他和欧亨利、契诃夫并称为世界三大短篇小说巨匠。
[判断题] *对错(正确答案)3、1议论文中论据与论点的关系是证明与被证明的关系。
[判断题] *对(正确答案)错4、1《我的空中楼阁》中写道:往返于快乐与幸福之间,哪儿还有不好走的路呢?这句话是说小屋不仅仅是物,还是作者理想境界的化身,是作者快乐与幸福的源泉,寄托了作者热爱自己的小屋,热爱自由快乐的生活,保持独立的人格的思想感情。
[判断题] *对(正确答案)错5、1“积土成山,风雨兴焉”的下一句是“积水成渊,蛟龙生焉”。
[判断题] *对(正确答案)错6、下列选项中加着重号字注音正确的一项是()[单选题] *A、槁暴pù輮使之然róu舟楫jì舆马yúB、蛟龙jiāo跬步kuǐ骐骥jì爪牙zhǎo(正确答案)C、镂金lóu 弩马nǔ洞穴xué生非异也xìngD、跂而望qì锲而不舍qì二螯áo 参省乎己xǐng7、1“小王一把拽住正准备闯红灯的老伯说:‘你活得不耐烦了?真是为老不尊!’”这句话中小王使用的语言不得体。
[判断题] *对错(正确答案)8、根据《红楼梦》的内容,完成下面的题目。
《红楼梦》中有许多重要章节,对于表现人物性格、推动情节发展有着重要的作用。
请选择人物序号填写在空格处。
《红楼梦》中,醉卧芍药裀的是()[单选题] *A.贾宝玉B.林黛玉C.王熙凤D.史湘云(正确答案)9、下面中括号内的字的注音完全正确的一组是()[单选题] *A.[溺]水(ruò)竹[筏](fá)倒[毙](bì)B.保[佑](yòu)[墓]地(mù)褴[褛](lǚ)(正确答案)C.[混]杂(hùn)埋[藏](cáng)[笼]罩(lóng)D.吹[嘘](xū)[煞]白(shà)[措]施(chuò)10、下列词语中,加着重号字的读音完全相同的一项是()[单选题] *A、翩然偏执扁舟翩跹(正确答案)B、阡陌陷阱纤维纤夫C、缥缈剽窃漂白饿殍D、点缀辍学拾掇赘述11、1介绍工艺流程一般按照工序的先后顺序逐一介绍,突出每个步骤的操作要领。

2025-高考科学复习创新方案-数学-提升版第八章第1讲基本立体图形及其直观图[课程标准]1.认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.2.能用斜二测画法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合)的直观图.1.多面体、旋转体的定义(1)01平面多边形围成的几何体叫多面体.(2)一条平面曲线(包括直线)02一条定直线旋转所形成的03旋转面,封闭的旋转面围成的几何体叫做旋转体.2.棱柱的概念及其分类(1)棱柱的概念04互相平行,05四边形,并且相邻两个四边形的公06互相平行,由这些面所围成的多面体叫做棱柱.(2)棱柱的分类①按底面多边形边数来分:三棱柱、四棱柱、五棱柱……②按侧棱是否与底面垂直07直棱柱,08斜09正棱柱,底面是平行四边形的四棱柱也10平行六面体.3.棱锥的概念及其分类(1)棱锥的概念有一个面是11多边形,其余各面都是有一个公共顶点的12三角形,由这些面所围成的多面体叫做棱锥.(2)棱锥的分类①按底面多边形的边数分:三棱锥、四棱锥……②底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做13正棱锥.4.棱台的概念及其分类(1)棱台的概念用一个14平行于棱锥底面的平面去截棱锥,底面和截面之间那部分多面体叫做棱台.(2)棱台的分类由三棱锥、四棱锥、五棱锥……截得的棱台分别为三棱台、四棱台、五棱台……5.圆柱、圆锥、圆台、球的概念及表示定义图形及表示圆柱以15矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱,如图中圆柱表示为圆柱O′O圆锥以16直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体,如图中圆锥表示为圆锥SO圆台用17平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台,如图中圆台表示为圆台O′O球 18半圆以它的直径所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球,如图中的球表示为球O6.简单组合体(1)概念由19简单几何体组合而成的几何体叫做简单组合体.(2)两种构成形式①由简单几何体20拼接而成;②由简单几何体21截去或挖去一部分而成.7.直观图(1)画法:常用22斜二测画法.(2)用斜二测画法画水平放置的平面图形的直观图的步骤1.斜二测画法中的“三变”与“三不变”“三变”⎩⎪⎨⎪⎧坐标轴的夹角改变与y 轴平行的线段的长度变为原来的一半图形改变“三不变”⎩⎪⎨⎪⎧平行性不改变与x ,z 轴平行的线段的长度不改变相对位置不改变2.直观图与原图形面积的关系S 直观图=24S 原图形(或S 原图形=22S 直观图).1.下列结论正确的是( )A .侧面都是等腰三角形的三棱锥是正三棱锥B .六条棱长均相等的四面体是正四面体C .有两个侧面是矩形的棱柱是直棱柱D .用一个平面去截圆锥,底面与截面之间的部分叫圆台答案 B解析 底面是等边三角形,且各侧面三角形全等,这样的三棱锥才是正三棱锥,A 错误;斜四棱柱也可能有两个侧面是矩形,C 错误;截面平行于底面时,底面与截面之间的部分才叫圆台,D 错误.故选B.2.如图所示,△A ′B ′C ′是水平放置的△ABC 的直观图,则在△ABC 的三边及中线AD 中,最长的线段是( )A .ABB .ADC .BCD .AC答案 D解析 △ABC 是直角三角形,且∠ABC =90°,则AC >AB ,AC >AD ,AC >BC .故选D.3.(人教B 必修第四册11.1.1练习A T 4改编)以下利用斜二测画法得到的结论中,正确的是( )A .相等的角在直观图中仍相等B .相等的线段在直观图中仍相等C .平行四边形的直观图是平行四边形D.菱形的直观图是菱形答案 C解析根据斜二测画法的规则可知,平行于坐标轴的直线平行性不变,平行于x轴的线段长度不变,平行于y轴的线段长度减半,故A,B,D错误;对于C,根据平行性不变原则,平行四边形的直观图仍然是平行四边形,C正确.故选C.4.(多选)(人教B必修第四册11.1.1练习A T1(3)改编)如图是一个正方体的平面展开图,将其复原为正方体后,互相重合的点是()A.A与B B.D与EC.B与D D.C与F答案ABD解析将平面展开图还原成正方体如图所示,所以互相重合的点是A与B,D与E,C与F.故选ABD.5. (人教A必修第二册习题8.1 T8改编)如图所示,长方体ABCD-A′B′C′D′被截去一小部分,其中EH∥A′D′,则剩下的几何体是()A.棱台B.四棱柱C.五棱柱D.简单组合体答案 C解析由几何体的结构特征知,剩下的几何体为五棱柱.故选C.考向一空间几何体的结构特征例1下列说法正确的是()A.有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱B.四棱锥的四个侧面都可以是直角三角形C.有两个平面互相平行,其余各面都是梯形的多面体是棱台D.棱台的各侧棱延长后不一定交于一点答案 B解析A错误,如图1;B正确,如图2,其中PD⊥底面ABCD,且底面ABCD 是矩形,可以证明∠P AB,∠PCB都是直角,这样四个侧面都是直角三角形;C 错误,如图3;D错误,由棱台的定义知,其侧棱延长后必相交于同一点.故选B.识别空间几何体的两种方法定义法紧扣定义,由已知构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本要素,根据定义进行判定反例法通过反例对结构特征进行辨析,要说明一个结论是错误的,只要举出一个反例即可1.下列结论正确的是()A.各个面都是三角形的几何体是三棱锥B.夹在圆柱的两个平行截面间的几何体还是一个旋转体C.若正棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥D.圆锥的顶点与底面圆周上任意一点的连线都是母线答案 D解析由图1知,A错误;如图2,当两个平行平面与底面不平行时,截得的几何体不是旋转体,B错误;若六棱锥的所有棱长都相等,则底面多边形是正六边形,由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长,C 错误;由母线的概念知,D正确.故选D.2.(多选)如图,将装有半槽水的长方体水槽固定底面一边后倾斜一个角度,则倾斜后水槽中的水形成的几何体可以是()A.四棱柱B.四棱台C.三棱柱D.三棱锥答案AC解析根据题图,因为有水的部分始终有两个平面平行,而其余各面都易证是平行四边形,因此形成的几何体是四棱柱或三棱柱.故选AC.考向二平面图形与其直观图的关系例2(多选)(2023·朝阳建平实验中学月考)如图所示,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=2O′B′=2,则以下说法正确的是()A.△ABC是钝角三角形B.△ABC的面积是△A′B′C′的面积的2倍C.△ABC是等腰直角三角形D.△ABC的周长是4+4 2答案CD解析根据斜二测画法可知,在原图形中,O为CA的中点,AC⊥OB,因为O′C′=O′A′=2O′B′=2,所以CO=AO=2,AC=4,OB=2,则△ABC是斜边为4的等腰直角三角形,如图所示,所以△ABC的周长是4+42,面积是4,故A错误,C,D正确;由斜二测画法可知,△ABC的面积是△A′B′C′的面积的22倍,故B错误.故选CD.在斜二测画法中,要确定关键点及关键线段.平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半.倍.注意:直观图面积是原图形面积的24用斜二测画法画出的某平面图形的直观图如图,边AB平行于y′轴,BC,AD平行于x′轴.已知四边形ABCD的面积为2 2 cm2,则原平面图形的面积为________cm2.答案8解析解法一:依题意可知∠BAD=45°,则原平面图形为直角梯形,上、下底的长分别与BC,AD相等,高为梯形ABCD的高的22倍,所以原平面图形的面积为8 cm2.解法二:依题意可知,S直观图=22(cm2),故S原图形=22S直观图=8(cm2).多角度探究突破考向三空间几何体的展开图和截面图角度空间几何体的展开图问题例3某圆柱的高为2,底面周长为16,M,N分别是圆柱上、下底面圆周上的两点,O为下底面圆的圆心,ME是圆柱的母线,OE⊥ON,如图所示,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.217 B.2 5C.3 D.2答案 B解析圆柱的侧面展开图及M,N的位置(N为EP的四等分点)如图所示,连接MN,则图中MN即为M到N的最短路径.EN=12+EN2=22+42=2 5.故选B.4×16=4,EM=2,∴MN=EM角度空间几何体的截面问题例4某同学在参加《通用技术》实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为43的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),若其中一个截面圆的周长为4π,则该球的半径是()A.2 B.4C.2 6 D.4 6答案 B解析设截面圆的半径为r,球的半径为R,则球心到某一截面的距离为正方体棱长的一半,即23,根据截面圆的周长可得4π=2πr,得r=2,故由题意知R2=r2+(23)2,即R2=22+(23)2=16,所以R=4.故选B.(1)通常利用空间几何体的表面展开图解决以下问题:①求几何体的表面积或侧面积;②求几何体表面上任意两个点的最短表面距离.(2)求解与截面有关的问题的关键是确定截面的形状,并从几何体中获取相关的数据进行计算.(3)作多面体截面的关键在于确定截点,有了位于多面体同一表面上的两个截点即可连接成截线,从而得到截面.1.如图,已知正三棱柱ABC-A1B1C1的底面边长为1 cm,高为5 cm,若一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点,则该质点所经最短路线的长为()A.12 cm B.13 cmC.61 cm D.15 cm答案 C解析如图所示,把侧面展开两周可得对角线最短,AA′1=62+52=61 (cm).故选C.2.(多选)已知正方体ABCD-A1B1C1D1的棱长为2,AC1⊥平面α.平面α截此正方体所得的截面有以下四个结论,其中正确的是()A.截面形状可能是正三角形B.截面的形状可能是正方形C.截面形状可能是正五边形D.截面面积的最大值为3 3答案AD解析对于A,当α截此正方体所得截面为B1CD1时满足,故A正确;对于B,由对称性得截面形状不可能为正方形,故B错误;对于C,由对称性得截面形状不可能是正五边形,故C错误;对于D,当截面为正六边形时面积最大,为6×34×(2)2=33,故D正确.故选AD.课时作业一、单项选择题1.将一个等腰梯形绕它的较长的底边所在的直线旋转一周,所得的几何体包括()A.一个圆台、两个圆锥B.两个圆台、一个圆柱C.两个圆柱、一个圆台D.一个圆柱、两个圆锥答案 D解析从较短的底边的端点向另一底边作垂线,两条垂线把等腰梯形分成了两个直角三角形,一个矩形,所以一个等腰梯形绕它的较长的底边所在直线旋转一周形成的是由一个圆柱、两个圆锥所组成的几何体,如图所示.故选D.2.(2024·衡水模拟)将12根长度相同的小木棍通过黏合端点的方式(不可折断),不可能拼成()A.正三棱柱B.正四棱锥C.正四棱柱D.正六棱锥答案 D解析A,B,C中的图形均可由12根长度相同的小木棍通过黏合端点的方式得到;对于D,因为正六边形的中心到六个顶点的距离都等于边长,所以正六棱锥的侧棱长总比底边长,故D不成立.故选D.3.(2023·济南一模)已知正三角形的边长为2,用斜二测画法画出该三角形的直观图,则所得直观图的面积为()A.24 B.64C.2 2 D.2 6答案 B解析S原图=12×2×2×sin60°=3,由斜二测画法中直观图和原图的面积的关系S直观图S原图=24,得S直观图=24×3=64.故选B.4.在我国古代数学名著《数学九章》中有这样一个问题:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”意思是“圆木长2丈4尺,圆周长为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺?”(注:1丈等于10尺),则这个问题中,葛藤长的最小值为()A.2丈4尺B.2丈5尺C.2丈6尺D.2丈8尺答案 C解析由题意,圆柱的侧面展开两次后是一条直角边(即圆木的高)长24尺,另一条直角边长5×2=10尺的矩形,因此葛藤长的最小值为242+102=26(尺),即为2丈6尺.故选C.5.通用技术老师指导学生制作统一规格的圆台形容器,用如图所示的圆环沿虚线剪开得到的一个半圆环(其中小圆和大圆的半径分别是1 cm和4 cm)制作该容器的侧面,则该圆台形容器的高为()A.32cm B.1 cmC. 3 cmD.332cm答案 D解析由已知圆台的侧面展开图为半圆环,不妨设上、下底面圆的半径分别为r cm,R cm(r<R),则2πr=π×1,2πR=π×4,解得r=12,R=2.所以圆台的轴截面为等腰梯形,其上、下底边的长分别为1 cm和4 cm,腰长为3 cm,即AD=1 cm,BC=4 cm,AB=3 cm,过点A作AH⊥BC,垂足为H,所以BH=32cm,AH=332cm,该圆台形容器的高为332cm.故选D.6.过棱长为1的正方体的一条体对角线作截面,则截得正方体的截面面积的最小值是()A.1 B. 2C.32 D.62答案 D解析取AA1的中点E,CC1的中点F,连接BE,ED1,D1F,FB,如图所示.四边形BED1F为过棱长为1的正方体的一条体对角线BD1所作截面的面积最小的截面,且四边形BED1F是菱形,其截面面积为12BD1·EF=12×3×2=62.故选D.7.如图所示,在单位正方体ABCD -A 1B 1C 1D 1的面对角线A 1B 上存在一点P ,使得AP +D 1P 取得最小值,则此最小值为( )A .2 B.2+62 C .2+ 2 D.2+ 2答案 D解析 如图所示,把对角面A 1C 绕A 1B 旋转至A 1BC ′D 1′,使其与△AA 1B 在同一平面上,连接AD 1′,则AD 1′=1+1-2×1×1×cos135°=2+2为所求的最小值.故选D.8.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5-14 B.5-12 C.5+14D.5+12答案 C解析 如图,O 为正方形ABCD 的中心,E 为CD 的中点.设CD =a ,PE =b ,则PO =PE 2-OE 2=b 2-a 24,由题意,得PO 2=12ab ,即b 2-a 24=12ab ,化简得4⎝ ⎛⎭⎪⎫b a 2-2·b a -1=0,解得ba =5+14(负值舍去).故选C.二、多项选择题9.(2023·池州期中)如图,我们常见的足球是由若干个正五边形和正六边形皮革缝合而成.如果我们把足球抽象成一个多面体,它有60个顶点,每个顶点发出的棱有3条,设其顶点数V 、面数F 与棱数E 满足V +F -E =2,据此判断,关于这个多面体的说法正确的是( )A .共有20个六边形B .共有10个五边形C .共有90条棱D .共有32个面答案 ACD解析 由题意,设共有m 个正五边形,n 个正六边形,即5m +6n3+(m +n )-5m +6n 2=2,解得m =12,故B 错误;∵顶点数V =5m +6n3=60,解得n =20,故A 正确;棱数E =5m +6n2=90,故C 正确;面数F =m +n =32,故D 正确.故选ACD.10.(2024·成都模拟)如图是由斜二测画法得到的水平放置的△ABC 的直观图△A 1B 1C 1,其中A 1B 1=B 1C 1,A 1D 1是B 1C 1边上的中线,则由图形可知下列结论中正确的是( )A .AB =BC =AC B .AD ⊥BC C .AB ⊥BC D .AC >AD >AB >BC答案 CD解析 由直观图知△ABC 为直角三角形,AB ⊥BC ,AB =2A 1B 1,BC =B 1C 1,D 为BC 的中点,如图所示,又A 1B 1=B 1C 1,故A ,B 错误,C ,D 正确.11.在通用技术课上,某小组将一个直三棱柱ABC-A1B1C1展开,得到的平面图如图所示,其中AB=4,AC=3,BC=AA1=5,M是BB1上的点,则()A.AM与A1C1是异面直线B.AC⊥A1MC.平面AB1C将三棱柱截成两个四面体D.A1M+MC的最小值是106答案ABD解析由题设,得如图1所示直三棱柱,由直三棱柱的结构特征知,AM与A1C1是异面直线,A正确;因为AA1⊥AC,BA⊥AC,且AA1∩BA=A,则AC⊥平面AA1B1B,又A1M⊂平面AA1B1B,故AC⊥A1M,B正确;由图1知,平面AB1C 将三棱柱截成四棱锥B1-ACC1A1和三棱锥B1-ABC,一个五面体和一个四面体,C错误;将平面AA1B1B和平面CC1B1B展开到一个平面内,如图2,当A1,M,C共线时,A1M+MC最小,为106,D正确.故选ABD.三、填空题12.若已知△ABC的直观图△A′B′C′是边长为a的正三角形,则△ABC的面积为_________.答案622a解析 如图所示是△ABC 的直观图△A ′B ′C ′.作C ′D ′∥y ′轴交x ′轴于点D ′,则C ′D ′对应△ABC 的高CD ,∴CD =2C ′D ′=2×2×C ′O ′=22×32a =6a .而AB =A ′B ′=a ,∴S △ABC =12a ·6a =62a 2.13.过年了,小张准备去探望奶奶,到商店买了一盒点心.为了美观,售货员用彩绳对点心盒做了一个捆扎(如图1所示),并在角上配了一个花结.彩绳与长方体点心盒均相交于棱的四等分点处.设这种捆扎方法所用绳长为l 1,一般的十字捆扎(如图2所示)所用绳长为l 2.若点心盒的长、宽、高之比为2∶2∶1,则l 1l2的值为________.答案22解析 设点心盒的长为2a (a >0),因为点心盒的长、宽、高之比为2∶2∶1,所以点心盒的宽、高分别为2a ,a .如题图1,绳长l 1=4×22a +4×2a =62a ,如题图2,绳长l 2=4×2a +4a =12a ,所以l 1l 2=62a 12a =22.14.中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为________.答案262-1解析先求面数,有如下两种解法.解法一:由“半正多面体”的结构特征及棱数为48可知,其上部分有9个面,中间部分有8个面,下部分有9个面,共有2×9+8=26个面.解法二:一般地,对于凸多面体,顶点数(V)+面数(F)-棱数(E)=2.(欧拉公式)由题图知,棱数为48的半正多面体的顶点数为24.故由V+F-E=2,得面数F=2+E-V=2+48-24=26.再求棱长.作中间部分的横截面,由题意知该截面为各顶点都在边长为1的正方形上的正八边形ABCDEFGH,如图,设其边长为x,则正八边形的边长即为棱长.连接AF,过H,G分别作HM⊥AF,GN⊥AF,垂足分别为M,N,则AM=MH=NG=NF=22x.又AM+MN+NF=1,∴22x+x+22x=1,∴x=2-1,即半正多面体的棱长为2-1.四、解答题15.一个圆台的母线长为12 cm,两底面面积分别为4π cm2,25π cm2,求:(1)圆台的高;(2)将圆台还原为圆锥后,圆锥的母线长.解(1)圆台的轴截面是等腰梯形ABCD(如图所示).由已知可得O 1A =2 cm ,OB =5 cm.又由题意知腰长AB =12 cm ,所以圆台的高AM =122-(5-2)2=315(cm).(2)如图所示,延长BA ,OO 1,CD ,交于点S ,设截得此圆台的圆锥的母线长为l cm ,则由△SAO 1∽△SBO ,可得l -12l =25,解得l =20,即截得此圆台的圆锥的母线长为20 cm.16.如图,圆台的上、下底面半径分别为5 cm ,10 cm ,母线长AB =20 cm ,从圆台母线AB 的中点M 拉一条绳子绕圆台侧面转到点A .求:(1)绳子的最短长度;(2)在绳子最短时,求上底面圆周上的点到绳子的最短距离.解 (1)如图,绳子的最短长度为侧面展开图中AM 的长度.由OB OB +AB =510,得OB =20 cm ,所以OA =40 cm ,OM =30 cm. 设∠BOB ′=θ,由2π×5=OB ·θ, 解得θ=π2.所以AM =OA 2+OM 2=50(cm), 即绳子的最短长度为50 cm.(2)过点O 作OQ ⊥AM 于点Q ,交BB ′︵于点P ,则PQ 的长度为所求最短距离.因为OA ·OM =AM ·OQ ,所以OQ =24 cm.故PQ =24-20=4(cm),即上底面圆周上的点到绳子的最短距离为4 cm.17.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是π,3=π,故其总曲率为4π.所以正四面体在各顶点的曲率为2π-3×π3(1)求四棱锥的总曲率;(2)若多面体满足:顶点数-棱数+面数=2,证明:这类多面体的总曲率是常数.解(1)由题意可知,四棱锥的总曲率等于四棱锥各顶点的曲率之和.可以从整个多面体的角度考虑,所有与顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知,四棱锥共有5个顶点,5个面,其中4个面为三角形,1个面为四边形.所以四棱锥的表面内角和为4个三角形,1个四边形的所有内角和,则其总曲率为2π×5-(4π+2π)=4π.(2)证明:设顶点数、棱数、面数分别为n,l,m,所以有n-l+m=2.设第i个面的棱数为x i,所以x1+x2+…+x m=2l,所以总曲率为2πn-π[(x1-2)+(x2-2)+…+(x m-2)]=2πn-π(2l-2m)=2π(n-l+m)=4π,所以这类多面体的总曲率是常数.。
建筑工程识图智慧树知到课后章节答案2023年下酒泉职业技术学院酒泉职业技术学院绪论单元测试1.新世纪环球中心以()为设计主题。
A:海浪B:鲸C:海洋D:海鸥答案:海洋2.成都新世纪环球中心是有世界著名建筑大师()设计的。
A:安东尼·高迪B:戴维·菲舍尔C:贝聿铭D:扎哈·哈迪德答案:扎哈·哈迪德3.哈利法塔的设计为()建筑风格A:基督教 B:佛教 C:道教D:伊斯兰教答案:伊斯兰教4.北京中信大厦是仿照古代礼器“尊”进行设计()。
A:对 B:错答案:对5.迪拜旋转摩天大楼能够360°旋转()。
A:对 B:错答案:对任务一测试1.一套完整的施工图包括()。
A:设备施工图B:建筑施工图 C:结构施工图答案:设备施工图;建筑施工图;结构施工图2.建筑工程图的线型包括有()等。
A:曲线 B:折断线C:波浪线 D:实线 E:虚线答案:折断线;波浪线;实线;虚线3.在建筑工程图样上,尺寸的组成包括( )。
A:尺寸数字B:尺寸线 C:尺寸界线 D:尺寸起止符号 E:尺寸大小答案:尺寸数字;尺寸线;尺寸界线;尺寸起止符号4.建筑施工图简称“建施”的图样通常包括()。
A:建筑立面图B:建筑平面图 C:首页和总平面图 D:基础平面图 E:建筑详图答案:建筑立面图;建筑平面图;首页和总平面图;建筑详图5.在建筑工程图样上,尺寸标注中要用细实线表示的部分有()。
A:尺寸数字 B:尺寸起止符号 C:尺寸大小D:尺寸线 E:尺寸界线答案:尺寸线;尺寸界线任务二测试1.建筑设计说明中并不对建筑的高度进行任何说明。
()A:错 B:对答案:错2.工程做法表只对室内部分的装饰装修做法进行详细说明。
()A:对 B:错答案:错3.建筑施工图上一般注明的标高是()。
A:绝对标高和相对标高B:绝对标高C:相对标高D:要看图纸上的说明答案:相对标高4.建筑工程图中尺寸单位,总平面图和标高单位用()为单位。
第十一章综合测试一、选择题1.已知两个平面相互垂直,下列命题①一个平面内已知直线必垂直于另一个平面内的任意一条直线②一个平面内已知直线必垂直于另一个平面内的无数条直线③一个平面内任意一条直线必垂直于另一个平面④过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面其中正确命题个数是()A.1B.2C.3D.42.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径,“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式d»,人们还用p»L判断,下列近似公式中最精确的一个是()过一些类似的近似公式,根据 3.14159A.d»B.d»C.d»D.d»∥的充要条件是()3.设a,b为两个平面,则a bA.a内有无数条直线与b平行B.a内有两条相交直线与b平行C.a,b平行于同一条直线D.a,b垂直于同一平面4.如图,在直角梯形SABC中,90^交SC于点D,以AD为折痕把ABC BCS°Ð=Ð=,过点A作AD SC-的的体积最大时,则下列命题中正确的个数是()△折起,当几何体S ABCDSAD①AC SB^②AB∥平面SCD③SA与平面SBD所成的角等于SC与平面SBD所成的角④AB与SC所成的角等于DC与SA所成的角A.4B.3C.2D.15.(多选题)设l为直线,a,b是两个不同的平面,下列命题中错误的是()A .若l a ∥,l b ∥,则a b∥B .若l a ^,l b ^,则a b ∥C .若l a ^,l b ∥,则a b ∥D .若a b ^,l a ∥,则l b^6.(多选题)如图正方体ABCD —A 1B 1C 1D 1的棱长为a ,以下结论正确的是()A .异面直线A 1D 与AB 1所成的角为60°B .直线A 1D 与BC 1垂直C .直线A 1D 与BD 1平行D .三棱锥A —A 1CD 的体积为316a 二、填空题7.一个正方体内接于一个球(即正方体的8个顶点都在球面上),过球心作一截面,则截面的图形可能是________.8.现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2,高为8的圆柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.9.在正方体ABCD —A'B'C'D'中,过对角线BD'的一个平面交AA'于点E ,交CC'于点F ,则:①四边形BFD'E 一定是平行四边形;②四边形BFD'E 有可能是正方形;③四边形BFD'E 在底面ABCD 内的投影一定是正方形;④平面BFD'E 有可能垂直于平面BB'D .以上结论正确的为________.(写出所有正确结论的编号)10.如图所示,以等腰直角三角形ABC 斜边BC 上的高AD 为折痕,使ABD △和ACD △折成互相垂直的两个平面,则:(1)BD与CD的关系为________;(2)BACÐ=________.三、解答题11.如图,直四棱柱ABCD—A1B1C1D1的底面是菱形,14AA=,2AB=,60BADÐ=°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.12.如图,在三棱锥P—ABC中,90ACBÐ=°,PA^底面ABC.(1)求证:平面PAC^平面PBC;(2)若AC BC PA==,M是PB的中点,求AM与平面PBC所成角的正切值.第十一章综合测试答案解析一、1.【答案】B【解析】由题意,对于①,当两个平面垂直时,一个平面内的不垂直于交线的直线不垂直于另一个平面内的任意一条直线,故①错误;对于②,设平面m a b =I 平面,n a Ì,l b Ì,Q 平面a ^平面b ,\当l m ^时,必有l a ^,而n a Ì,l n \^,而在平面b 内与l 平行的直线有无数条,这些直线均与n 垂直,故一个平面内的已知直线必垂直于另一个平面内的无数条直线,即②正确;对于③,当两个平面垂直时,一个平面内的任一条直线不垂直于另一个平面,故③错误;对于④,当两个平面垂直时,过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面,这是面面垂直的性质定理,故④正确;故选:B 。
备课素材【教材分析】全文条理清晰,重点突出,语言平实流畅,描写细致。
介绍了埃及金字塔的形状及其建筑历史,写出了外观宏伟、结构精巧的特点以及建造金字塔所采用的办法,热情讴歌了古埃及人民杰出的智慧和超人的才干。
借物写人,借“金字塔”建筑,讴歌古埃及人民的智慧和才干以及勤劳。
两篇课文在结构、内容上都有许多相似之处,许多内容互相印证。
【作者介绍】穆青(1921---2003),新华通讯社原社长、当代著名新闻记者穆青,他的新闻作品、新闻主张和新闻实践,均为20世纪中国新闻史上不可或缺的重要部分。
【与文章相关的资料介绍】古埃及古埃及,四大文明古国之一,位于非洲东北部尼罗河中下游地区,是典型的水力帝国,受宗教影响极大,举世闻名的金字塔就是古埃及人对永恒观念的一种崇拜产物,也是法老的陵墓。
除了金字塔以外,狮身人面像、木乃伊也是埃及的象征。
古埃及文明形成于6000年前(公元前4000年)左右,古埃及前王朝开始于5500年前(公元前35世纪)左右时美尼斯统一上下埃及建立第一王朝,终止于公元前343年波斯再次征服埃及。
金字塔金字塔在埃及和美洲等地均有分布。
现在的尼罗河下游,散布着约80座金字塔遗迹。
最大的是开罗郊区胡夫的三座金字塔。
狮身人面像狮身人面像,是一座位在卡夫拉金字塔旁的雕像,外型是一个狮子的身躯和人的头。
位于埃及开罗西萨市南郊沙漠中,在金字塔的前方,为著名的景点。
古埃及人在“大金字塔”附近建造了一座“人面狮身像”。
至今仍然没有人确定建造这座由“狮身”与“人面”组成的巨大石雕的原因。
一些人相信“狮身人面像”可能是金字塔的守护神,另一些则认为它是古埃及伟大文明的象征。
尼罗河尼罗河是一条流经非洲东部与北部的河流,自南向北注入地中海。
尼罗河长6670公里,是世界上最长的河流。
尼罗河从苏丹首都向北穿过苏丹和埃及,所经过的地方均是沙漠。
从古代开始埃及的文明就依靠尼罗河而形成和兴旺。
除海港和海岸附近的城市外埃及所有的城市和大多数居民住在阿斯旺以北的尼罗河畔,几乎所有的古埃及遗址均位于尼罗河畔。
1全国第三批新高考2024-2024年物理核心考点压轴计算题汇编学校:_______ 班级:__________姓名:_______ 考号:__________(满分:100分时间:75分钟)总分栏题号一二三四五六七总分得分评卷人得分一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题有关量子理论及相关现象,下列说法中正确的是( )A.能量量子化的观点是爱因斯坦首先提出的B.在光电效应现象中,遏止电压与入射光的频率成正比C.一个处于n=4激发态的氢原子向基态跃迁时,最多能辐射出3种频率的光子D.α射线、β射线、γ射线都是波长极短的电磁波第(2)题2019年1月,我国嫦娥四号探测器成功在月球背面软着陆,在探测器“奔向”月球的过程中,用h表示探测器与地球表面的距离,F表示它所受的地球引力,能够描F随h变化关系的图像是( )A.B.C.D.第(3)题如图所示,正四面体的四个顶点ABCD分别固定一个点电荷,A点电荷量为,其余点电荷为,E、F、H点分别为AB、AD和BC的中点,下列说法正确的是( )A.E点场强大于F点的场强B.E点场强小于H点的场强C.正四面体中心的电势低于F点电势D.将正电荷沿直线从H点移到F点,电势能一直降低第(4)题倾角为的光滑绝缘斜面下半部分存在垂直斜面向上的匀强磁场,一半径为r的单匝圆形金属线圈用绝缘细绳挂在斜面上,圆心为O点,a、b是圆环上的两点,线圈总电阻为R。
如图所示,aOb连线恰好与磁场边界重合,从开始,磁感应强度B随时间t变化的规律为(k为常数,且)。
磁场变化过程中线圈始终未离开斜面,下列说法正确的是( )A.线圈中电流方向为逆时针B.时刻穿过线圈的磁通量为C.ab两端的电压为D.线圈中的感应电流为第(5)题排球运动员在某次发球中,左手托球由静止开始竖直向上运动时,排球脱离左手继续向上运动达到最高点,然后下落被右手击出。
加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第十章综合测试基础练习一、选择题1.复数()2z m m mi =++(m ∈R ,i 为虚数单位)是纯虚数,则实数m 的值为( ) A.0或1−B.0C.1D.1−2.在复平面内,复数2334ii−+−(i 是虚数单位)所对应的点位于( ) A.第一象限B.第二象限C.第三象限D.第四象限3.已知平行四边形OABC ,O 、A 、C 三点对应的复数分别为0、12i +、32i −,则向量 AB 的模 ||AB 等于( )B.C.44.设122iz i −=+,2(1)(1)z i i =+−,12z z z =+,则z =( ) A.435i − B.3455i + C.13445i −D.13455i +5.已知复数1cos sin 1212z i ππ⎫+⎪⎭,2cos sin 66z i ππ⎫+⎪⎭,则12z z 的代数形式是( )cos sin 44i ππ⎫+⎪⎭cos sin 1212i ππ⎫+⎪⎭二、填空题6.已知复数()21 2(4)z a a i =−+−,()21 2(4)z a a i =−+−,且12 z z −为纯虚数,则a =________。