九年级数学方差与标准差
- 格式:docx
- 大小:54.88 KB
- 文档页数:4
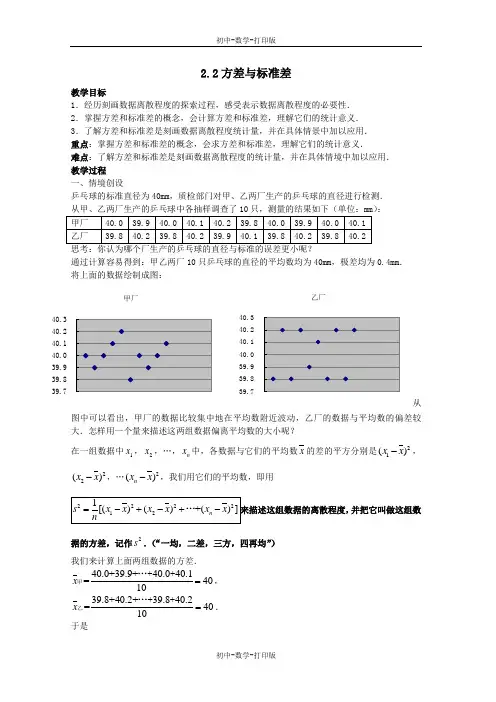
2.2方差与标准差教学目标1.经历刻画数据离散程度的探索过程,感受表示数据离散程度的必要性.2.掌握方差和标准差的概念,会计算方差和标准差,理解它们的统计意义.3.了解方差和标准差是刻画数据离散程度统计量,并在具体情景中加以应用.重点:掌握方差和标准差的概念,会求方差和标准差,理解它们的统计意义.难点:了解方差和标准差是刻画数据离散程度的统计量,并在具体情境中加以应用. 教学过程一、情境创设乒乓球的标准直径为40mm ,质检部门对甲、乙两厂生产的乒乓球的直径进行检测.:通过计算容易得到:甲乙两厂10只乒乓球的直径的平均数均为40mm ,极差均为0.4mm . 将上面的数据绘制成图: 乙厂39.739.839.940.040.140.240.3从图中可以看出,甲厂的数据比较集中地在平均数附近波动,乙厂的数据与平均数的偏差较大.怎样用一个量来描述这两组数据偏离平均数的大小呢?在一组数据中1x ,2x ,…,n x 中,各数据与它们的平均数x 的差的平方分别是21()x x -,22()x x -,…2()n x x -,我们用它们的平均数,即用2222121[()()+()]n s x x x x x x n=-+-+-…来描述这组数据的离散程度,并把它叫做这组数据的方差,记作2s .(“一均,二差,三方,四再均”)我们来计算上面两组数据的方差. 40.0+39.9+40.040.1=4010x =甲…++, 39.8+40.2+39.840.2=4010x =乙…++. 于是甲厂39.739.839.940.040.140.240.3222221[(40.040)(40.140)(40.040)(39.940)]=0.01210s =-+-++-+-甲…, 222221[(39.840)(40.240)(40.240)(39.840)]=0.03410s =-+-++-+-乙…. 22s s <甲乙,说明甲组数据的离散程度较小.通常我们也可以用方差的算术平方根,即数据的标准差,记作s .例如上述数据的标准差分别是:0.11s ≈甲,0.18s ≈乙. 通常,一组数据的方差或者标准差越小,这组数据的离散程度越小,这组数据就越稳定. 二、例题讲解《学与练》P3例1、例2、拓展提升方差的单位是数据单位的平方,标准差的单位与数据单位一致.三、课堂练习四、小结1.我们知道极差只能反映一组数据中两个 之间的大小情况,而对其他数据的波动情况不敏感.2.描述一组数据的离散程度可以采取许多方法,在统计中常采用先求这组数据的 ,再求这组数据与 的差的 的平均数,用这个平均数来衡量这组数据的波动性大小,即2222121[()()+()]n s x x x x x x n=-+-+-… . 3.一组数据方差的算术平方根叫做这组数据的 。


初中数学方差标准差公式(一)方差的计算、知识点归纳方差在考试中考察不是很难,记住基本公式往里带就能解答正确,但是方差的概念让不少同学为此很是头痛。
那方差到底是什么,怎样计算呢,下面小编就为大家整理一些题型和解题方法技巧。
初一、概念和公式方差的概念与计算公式,例1 两人的5次测验成绩如下:X: 50,100,100,60,50 E(X)=72;Y: 73, 70, 75,72,70 E(Y)=72。
平均成绩相同,但X 不稳定,对平均值的偏离大。
方差描述随机变量对于数学期望的偏离程度。
单个偏离是消除符号影响方差即偏离平方的均值,记为D(X):直接计算公式分离散型和连续型,具体为:这里是一个数。
推导另一种计算公式得到:“方差等于平方的均值减去均值的平方”。
其中,分别为离散型和连续型计算公式。
称为标准差或均方差,方差描述波动程度。
基本定义:设X是一个随机变量,若E{[X-E(X)]2}存在,则称E{[X-E(X)]2}为X的方差,记为D(X),Var(X)或DX。
即D(X)=E{[X-E(X)]2}称为方差,而σ(X)=D(X)0.5(与X有相同的量纲)称为标准差(或均方差)。
即用来衡量一组数据的离散程度的统计量。
方差刻画了随机变量的取值对于其数学期望的离散程度。
(标准差、方差越大,离散程度越大。
否则,反之)若X的取值比较集中,则方差D(X)较小,若X的取值比较分散,则方差D(X)较大。
因此,D(X)是刻画X取值分散程度的一个量,它是衡量取值分散程度的一个尺度。
当数据分布比较分散(即数据在平均数附近波动较大)时,各个数据与平均数的差的平方和较大,方差就较大;当数据分布比较集中时,各个数据与平均数的差的平方和较小。
因此方差越大,数据的波动越大;方差越小,数据的波动就越小二、计算方法和原理若x1,x2,x3......xn的平均数为m则方差方差公式方差公式例1 两人的5次测验成绩如下:X: 50,100,100,60,50 E(X )=72;Y: 73, 70, 75,72,70 E(Y )=72。

初中数学知识归纳方差与标准差的应用初中数学知识归纳:方差与标准差的应用统计学是一门研究和分析数据的学科,方差和标准差是其中重要的统计量。
本文将介绍方差和标准差的定义、计算方法以及在实际生活中的应用。
1. 方差的定义与计算方法方差是衡量数据分散程度的统计量。
对于一组数据,假设有n个观测值,分别为x1, x2, ..., xn,其平均值为x。
方差的计算公式如下:方差 = ((x1 - x)^2 + (x2 - x)^2 + ... + (xn - x)^2) / n其中,(x1 - x)^2表示每一个观测值与平均值的差的平方,然后将这些平方差相加,并除以观测值的个数n。
2. 标准差的定义与计算方法标准差是方差的平方根,它表示数据分散程度的一种度量。
标准差的计算公式如下:标准差= √方差标准差是方差开方得到的结果,它与原始数据具有相同的单位。
3. 方差与标准差的应用方差和标准差在实际应用中具有广泛的意义,在以下几个方面得到了广泛的应用:3.1 统计数据的比较方差和标准差可以用于比较不同数据集的分散程度。
如果两个数据集的方差或标准差相差很大,则说明它们的数据分布情况存在较大的差异。
3.2 风险评估在金融领域,方差和标准差用于评估投资的风险。
投资组合的方差和标准差越大,代表其风险越高,投资者需要更加谨慎。
3.3 质量控制在生产领域,方差和标准差可以用于衡量产品质量的一致性。
通过收集一批产品的相关数据,计算方差和标准差可以判断产品制造过程的稳定性,从而改进生产流程。
3.4 结果分析在调查研究中,方差和标准差可以帮助分析和解释结果的可靠性。
如果调查结果的方差或标准差较大,则说明数据的可靠性较低,需要进一步深入分析。
4. 实例说明为了更好地理解方差和标准差的应用,我们以学生成绩为例进行说明。
假设有一组学生的数学成绩如下:80, 85, 90, 75, 95。
首先,计算平均值:平均值x = (80 + 85 + 90 + 75 + 95) / 5 = 85然后,计算方差:方差 = ((80 - 85)^2 + (85 - 85)^2 + (90 - 85)^2 + (75 - 85)^2 + (95 -85)^2) / 5= (25 + 0 + 25 + 100 + 100) / 5= 50最后,计算标准差:标准差 = √方差= √50 ≈ 7.07通过计算,我们可以得出这组学生成绩的平均值为85,方差为50,标准差为7.07。
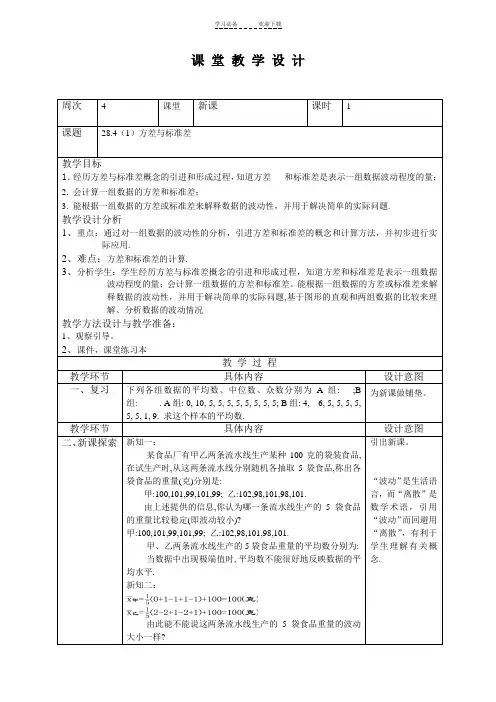
课堂教学设计周次 4 课型新课课时 1课题28.4(1)方差与标准差教学目标1.经历方差与标准差概念的引进和形成过程,知道方差和标准差是表示一组数据波动程度的量;2. 会计算一组数据的方差和标准差;3. 能根据一组数据的方差或标准差来解释数据的波动性,并用于解决简单的实际问题.教学设计分析1、重点:通过对一组数据的波动性的分析,引进方差和标准差的概念和计算方法,并初步进行实际应用.2、难点:方差和标准差的计算.3、分析学生:学生经历方差与标准差概念的引进和形成过程,知道方差和标准差是表示一组数据波动程度的量;会计算一组数据的方差和标准差。
能根据一组数据的方差或标准差来解释数据的波动性,并用于解决简单的实际问题,基于图形的直观和两组数据的比较来理解、分析数据的波动情况教学方法设计与教学准备:1、观察引导。
2、课件,课堂练习本教学过程教学环节具体内容设计意图一、复习下列各组数据的平均数、中位数、众数分别为A组:___;B组:_____. A组: 0, 10, 5, 5, 5, 5, 5, 5, 5, 5; B组: 4, 6, 5, 5, 5, 5,5, 5, 1, 9. 求这个样本的平均数.为新课做铺垫。
教学环节具体内容设计意图二、新课探索新知一:某食品厂有甲乙两条流水线生产某种100克的袋装食品,在试生产时,从这两条流水线分别随机各抽取5袋食品,称出各袋食品的重量(克)分别是:甲:100,101,99,101,99; 乙:102,98,101,98,101.由上述提供的信息,你认为哪一条流水线生产的5袋食品的重量比较稳定(即波动较小)?甲:100,101,99,101,99; 乙:102,98,101,98,101.甲、乙两条流水线生产的5袋食品重量的平均数分别为:当数据中出现极端值时,平均数不能很好地反映数据的平均水平.新知二:由此能不能说这两条流水线生产的5袋食品重量的波动大小一样?引出新课。

九年级数学方差与标准差Revised on November 25, 2020方差与标准差班级姓名学号学习目标:1、了解方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
4.经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验。
学习重点掌握方差与标准差的概念及计算公式,会用方差计算公式来比较两组数据的波动大小。
学习难点探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验。
教学过程一、情境引入:1.世乒赛派谁去你有什么办法厂:,,,,,(单位:mm),,,,;B厂:,,,,,,,,,。
怎么描述这些数据相对于它门的平均数的离散程度呢二、知识点在一组数据中x1,x2…xn,个数据与它们的平均数分别是(x1-x)2,(x2-x)2…,(x n-x)2我们用它们的平均数,即用S 2=[(x 1-x)2+(x 2-x)2+…+(x n -x)2] 来描述这组数据的离散程度,并把它叫做这组数据的方差。
在有些情况下,需要用方差的算术平方根,即来描述一组数据的离散程度,并把它叫做这组数据的标准差。
注意:一般来说,一组数据的方差或标准差越小,这组数据离散程度越小,这组数据越稳定。
三、试一试1、一组数据:2-,1-,0,x ,1的平均数是0,则x =.方差=2S .2、如果样本方差[]242322212)2()2()2()2(41-+-+-+-=x x x x S , 那么这个样本的平均数为.样本容量为.3、已知321,,x x x 的平均数=x 10,方差=2S 3,则3212,2,2x x x 的平均数为,方差为.4、样本方差的作用是()A 、估计总体的平均水平B 、表示样本的平均水平C 、表示总体的波动大小D 、表示样本的波动大小,从而估计总体的波动大小 四、例题:1.甲、乙两台机床生产同种零件,10天出的次品分别是 甲:0、1、0、2、2、0、3、1、2、4 乙:2、3、1、2、0、2、1、1、2、1分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好 思维点拨:方差是描述一组数据波动大小的特征数,可通过比较其大小判断波动的大小,方差越小越稳定,说明机床的性能较好。



初中数学知识归纳方差与标准差的概念和计算方差与标准差是初中数学中重要的统计学概念。
它们代表了一组数据的离散程度,对于分析和比较数据的差异非常有用。
本文将详细介绍方差与标准差的概念,并给出计算方法和实际应用示例。
一、方差的概念和计算方法方差是一组数据平均值与各个数据之间差异的平方的平均值。
它可以衡量数据的离散程度。
方差的计算公式如下:方差= (∑(xi-平均值)²)/n其中,xi代表数据中的每一个数值,平均值是数据的平均值,n是数据的个数。
用具体的例子来说明方差的计算过程。
假设我们有一组数列:2, 4, 6, 8, 10。
首先计算平均值,(2+4+6+8+10)/5 = 6。
然后依次计算每个数据与平均值之差的平方,并求和:((2-6)²+(4-6)²+(6-6)²+(8-6)²+(10-6)²)/5 = 8。
所以这组数列的方差为8。
方差的计算过程可能比较繁琐,为了简化计算,我们引入了标准差的概念。
二、标准差的概念和计算方法标准差是方差的平方根,它与方差一样,用来衡量数据的离散程度。
标准差的计算公式如下:标准差= √方差标准差的计算方法更加简单直观,它可以直接反映出数据集合的波动情况。
在前面的例子中,这组数据的标准差为√8,约等于2.83。
三、方差和标准差的应用举例方差和标准差在实际问题中有广泛的应用。
以下是一些具体的应用示例:1. 统计学研究:方差和标准差常用于统计学的研究中,可以帮助研究人员了解数据的分布情况、比较不同数据集的离散程度等。
2. 财务分析:方差和标准差可以用于财务分析中,帮助分析师评估不同投资组合的风险程度。
标准差越大,数据集合的波动性越高,风险也就越大。
3. 质量控制:在生产过程中,方差和标准差可以用来衡量产品质量的稳定性。
如果方差或标准差较大,说明产品质量波动较大,需进一步调整生产过程。
4. 教育评估:方差和标准差可以用于教育评估中,帮助评估学生的成绩分布情况、班级或学校的教学水平等。

苏科版数学九年级上册3.4 方差、标准差教学设计一. 教材分析苏科版数学九年级上册3.4 方差、标准差是本册的重点内容,也是难点内容。
这一节主要介绍了方差和标准差的概念,以及它们的计算方法。
方差是衡量一组数据波动大小的量,标准差是方差的平方根,用来衡量一组数据的离散程度。
本节内容对于学生来说比较抽象,需要通过大量的例子来帮助学生理解和掌握。
二. 学情分析九年级的学生已经学习了一元二次方程、不等式等基础知识,对于函数、统计等概念也有一定的了解。
但是,对于方差、标准差这样的抽象概念,学生可能难以理解。
因此,在教学过程中,需要通过具体的例子来帮助学生理解概念,并通过大量的练习来巩固知识。
三. 教学目标1.了解方差、标准差的概念,理解它们的意义。
2.学会计算方差、标准差的方法。
3.能够应用方差、标准差来解决实际问题。
四. 教学重难点1.方差、标准差的概念。
2.方差、标准差的计算方法。
3.应用方差、标准差解决实际问题。
五. 教学方法采用问题驱动法、案例教学法、小组合作法等教学方法。
通过具体的例子引出方差、标准差的概念,通过案例教学法讲解计算方法,通过小组合作法让学生互相讨论、交流,巩固知识。
六. 教学准备1.PPT课件。
2.相关案例资料。
3.练习题。
七. 教学过程1.导入(5分钟)通过一个具体的问题引出方差、标准差的概念。
例如,某学校九年级有甲、乙两个班级,在一次数学考试中,甲班平均分是80分,乙班平均分是82分,问这两个班的数学成绩是否存在显著性差异?2.呈现(10分钟)通过PPT课件呈现方差、标准差的定义和计算公式。
方差是衡量一组数据波动大小的量,标准差是方差的平方根,用来衡量一组数据的离散程度。
3.操练(10分钟)让学生分组讨论,每组找一个例子,计算其方差和标准差。
教师巡回指导,解答学生疑问。
4.巩固(10分钟)让学生独立完成练习题,教师选取部分题目进行讲解。
5.拓展(10分钟)让学生思考:方差、标准差在实际生活中有哪些应用?引导学生联系生活实际,举例说明。

九年级上册《方差与标准差》导学案数学教案
标题:九年级上册《方差与标准差》导学案
一、教学目标:
1. 学生能够理解并掌握方差和标准差的概念。
2. 学生能够熟练地计算一组数据的方差和标准差。
3. 学生能够运用方差和标准差来描述数据的离散程度,并能对不同数据集的离散程度进行比较。
二、教学重点难点:
1. 教学重点:方差和标准差的概念及其计算方法。
2. 教学难点:理解和运用方差和标准差描述数据的离散程度。
三、教学过程:
1. 导入新课:
通过实际生活中的例子引入课题,比如学生的考试成绩分布,引出描述数据集中趋势和离散程度的需求。
2. 新课讲解:
(1)介绍平均数作为描述数据集中趋势的一个指标,然后引出描述数据离散程度的需要。
(2)讲解方差的概念和计算方法,引导学生理解方差反映的是数据相对于平均数的偏离程度。
(3)讲解标准差的概念和计算方法,说明它是方差的平方根,更直观地反映了数据的离散程度。
3. 练习巩固:
设计一些练习题,让学生通过计算实例数据的方差和标准差,加深对方差和标准差的理解。
4. 小结:
总结本节课学习的主要内容,强调方差和标准差在描述数据离散程度中的作用。
5. 作业布置:
布置一些包含计算方差和标准差的题目,让学生在实践中进一步熟悉这两个概念。
四、教学反思:
在教学过程中,要关注学生的学习反馈,及时调整教学策略,以提高教学效果。
方差和标准差公式初中在初中数学的学习中,方差和标准差公式可是个有点小复杂但又特别重要的知识点。
先来说说方差吧,方差的公式是:$S^2 = \frac{1}{n}[(x_1 -\overline{x})^2 + (x_2 - \overline{x})^2 + \cdots + (x_n -\overline{x})^2]$ ,这里面的$n$表示样本数量,$\overline{x}$是样本的平均数,$x_1, x_2, \cdots, x_n$是各个样本值。
那标准差呢,其实就是方差的算术平方根,公式就是$S = \sqrt{\frac{1}{n}[(x_1 -\overline{x})^2 + (x_2 - \overline{x})^2 + \cdots + (x_n -\overline{x})^2]}$ 。
我记得有一次给学生们讲这部分内容的时候,那场面可真是有趣极了。
我在黑板上写下了一组数据:10, 12, 15, 18, 20。
然后问大家:“你们觉得这组数据的波动情况怎么样?” 有的同学说看起来好像不太稳定,有的同学则一脸茫然。
我笑着说:“那咱们就用今天学的方差和标准差公式来算算,看看能不能找到答案。
”我带着大家先算出这组数据的平均数,$\overline{x} = \frac{10 + 12 + 15 + 18 + 20}{5} = 15$ 。
接下来,一个个地计算$(x_i -\overline{x})^2$ 。
比如说,第一个数 10,$(10 - 15)^2 = 25$ ;第二个数 12,$(12 - 15)^2 = 9$ ;依此类推。
这时候,有个平时挺调皮的同学叫小王,他开始嘀咕了:“哎呀,老师,这也太麻烦啦!” 我笑着回应他:“别急别急,虽然现在麻烦点,但等你掌握了,就能轻松看出数据的波动规律啦。
” 大家算完之后,把这些结果加起来除以 5,就得到了方差。
再开个平方根,标准差也就出来啦。
标准差和方差的区别介绍在统计学中,标准差和方差是两个重要的概念。
它们都是用来度量数据的离散程度,但是具体的计算方式和解释有所不同。
本文将详细解释标准差和方差的定义、计算方法以及它们之间的区别。
方差的定义和计算方法方差是衡量随机变量离其期望值的预测精度的统计量。
它表示数据的离散程度或者变异程度。
方差的计算公式如下:方差= (∑(x-μ)^2) / N其中,x代表每个观测值,μ代表数据的平均值,N代表观测值的总数。
方差的单位是观测值数的平方。
方差的计算过程相对简单,只需要计算每个观测值与平均值的差的平方,并求和,最后除以观测值的总数即可得到方差的值。
方差越大,表示数据的离散程度越高。
标准差的定义和计算方法标准差是方差的平方根,用来衡量数据的离散程度或者波动程度。
标准差的计算公式如下:标准差= √方差标准差的单位和原始数据的单位相同。
标准差越大,表示数据的波动性越大,即数据的离散程度越高。
方差和标准差之间的关系方差和标准差之间存在着一定的数学关系。
标准差就是方差的平方根,即标准差的计算方法是对方差的结果开方得到的。
方差和标准差都是用来衡量数据的离散程度,但是它们的解释和使用上略有不同。
方差可以直接表示数据的离散程度,而标准差更容易理解和解释,因为标准差的单位和原始数据的单位一致。
在实际应用中,方差和标准差都有各自的优势和用途。
方差通常用于计算统计数据的离散程度,并且在一些数学模型中有着广泛的应用。
而标准差更易于解释和理解,因此在一些实际场景中更常用。
总结标准差和方差是两个重要的统计概念,用于衡量数据的离散程度。
方差是数据离其期望值的平均偏离程度的平方,标准差是方差的平方根。
方差和标准差都有各自的应用场景和优势,选择使用哪一个取决于具体的数据分布和分析需求。
无论是方差还是标准差,它们都是统计学中非常有用的工具,可以帮助我们理解和分析数据的离散程度,进而得出有关数据的结论。
因此,在统计分析领域中对于方差和标准差的理解和应用至关重要。
初中方差和标准差公式在咱们初中数学的世界里,方差和标准差这两个家伙可是相当重要的角色呢!先来说说方差,方差的公式是:一组数据中各个数据与这组数据的平均数的差的平方的平均数。
哎呀,这话说起来有点绕口,咱举个例子就清楚啦。
比如说有一组数 5、8、10、12、15,它们的平均数是(5 + 8 + 10 + 12 + 15)÷ 5 = 10 。
那每个数与平均数 10 的差分别是 -5、-2、0、2、5 ,差的平方分别是 25、4、0、4、25 ,这些平方的平均数就是方差啦,算出来是(25 + 4 + 0 + 4 + 25)÷ 5 = 10 。
再看看标准差,它其实就是方差的平方根。
所以上面那组数据的标准差就是根号 10 。
还记得我之前教过的一个学生小明,他一开始对方差和标准差那是一头雾水。
有一次做作业,碰到了一道求方差的题目,他愣是算错了好几遍。
我就坐在他旁边,看着他眉头紧锁,嘴里还念念有词:“这到底咋算呀?”我就耐心地给他一步一步讲解,告诉他先求出平均数,再算每个数与平均数的差,然后平方、求和、再求平均。
小明听着听着,眼睛突然亮了起来,“哦!老师,我懂啦!”然后他重新算了一遍,终于算对了,那高兴劲儿,就像解开了一道超级难题似的。
方差和标准差在实际生活中的用处可大着呢!比如说,在比较两个班级学生的成绩稳定性时,就可以用方差和标准差。
如果一个班级成绩的方差小,说明这个班级学生的成绩比较稳定,大家的水平都差不多;要是方差大,那就说明成绩参差不齐,有的同学特别好,有的同学可能就稍微落后一些。
再比如,在工厂生产零件的时候,通过测量零件的尺寸,计算其方差和标准差,可以判断生产过程是否稳定,产品质量是否可靠。
还有在体育比赛中,比如射击比赛,运动员每次射击的成绩就可以通过方差和标准差来衡量其稳定性。
如果一个运动员成绩的标准差小,说明他发挥很稳定,是个高手哟!总之,方差和标准差虽然看起来有点复杂,但只要咱们多做几道题,多联系实际想想,就能轻松掌握啦!就像小明一样,只要认真学,一定能搞明白的。
2.2方差
与标准差
班级姓名学号
学习目标:
1、了解方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
4.经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验。
学习重点
掌握方差与标准差的概念及计算公式,会用方差计算公式来比较两组数据的波动大小。
学习难点
探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验。
教学过程 一、情境引入:
1.世乒赛派谁去?你有什么办法?
2.A 厂:40.0,39.9,40.0,40.1,40.2,(单位:mm) 39.8,40.0,39.9,40.0,40.1;
B 厂:39.8,40.2,39.8,40.2,39.9, 40.1,39.8,40.2,39.8,40.2。
怎么描述这些数据相对于它门的平均数的离散程度呢? 二、知识点
在一组数据中x1,x2…xn ,个数据与它们的平均数分别是(x 1-x)2,(x 2-x)2…,(x n -x)2
我们用它们的平均数,即用S 2=[(x 1-x)2+(x 2-x)2+…+(x n -x)2
]
来描述这组数据的离散程度,并把它叫做这组数据的方差。
在有些情况下,需要用方差的算术平方根,即
来描述一组数据的离散程度,并把它叫做这组数据的标准差。
注意:一般来说,一组数据的方差或标准差越小,这组数据离散程度越小,这组数据越稳定。
三、试一试
1、一组数据:2-,1-,0,x ,1的平均数是0,则x =.方差=2
S . 2、如果样本方差[]242322212
)2()2()2()2(4
1
-+-+-+-=x x x x S
,
那么这个样本的平均数为.样本容量为.
3、已知321,,x x x 的平均数=x 10,方差=2
S 3,则3212,2,2x x x 的平均数为,方差为. 4、样本方差的作用是()
A 、估计总体的平均水平
B 、表示样本的平均水平
C 、表示总体的波动大小
D 、表示样本的波动大小,从而估计总体的波动大小 四、例题:1.甲、乙两台机床生产同种零件,10天出的次品分别是 甲:0、1、0、2、2、0、3、1、2、4 乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
思维点拨:方差是描述一组数据波动大小的特征数,可通过比较其大小判断波动的大小,方差越小越稳定,说明机床的性能较好。
2.已知,一组数据x 1,x 2,……,x n 的平均数是10,方差是2, ①数据x 1+3,x 2+3,……,x n +3的平均数是方差是, ②数据2x 1,2x 2,……,2x n 的平均数是方差是, ③数据2x 1+3,2x 2+3,……,2x n +3的平均数是方差是,
思维点拨:本题可通过相关计算公式进行实际计算,得出相应的结果。
点评:你能找出数据的变化与平均数、方差的关系吗?
四、归纳总结:
【课后作业】
班级姓名学号
1、(08,大连)随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为:,,,,则小麦长势比较整齐的试验田是。
13=甲x 13=乙x 6.3S
2
=甲
8.15S 2=乙
2、在统计中,样本的标准差可以反映这组数据的()
A .平均状态
B .分布规律
C .离散程度
D .数值大小
3、(08,嘉兴)已知甲、乙两组数据的平均数分别是80x =甲,90x =乙,方差分别是2
10S =甲,
2
5S =乙,比较这两组数据,下列说法正确的是()
A .甲组数据较好
B .乙组数据较好
C .甲组数据的极差较大
D .乙组数据的波动较小 4、下列说法正确的是()
A .两组数据的极差相等,则方差也相等
B .数据的方差越大,说明数据的波动越小
C .数据的标准差越小,说明数据越稳定
D .数据的平均数越大,则数据的方差越大 5、(08,河南)样本数据3,6,a ,4,2的平均数是3,则这个样本的方差是。
6、数据1x ,2x ,3x ,4x 的平均数为m ,标准差为5,那么各个数据与m 之差的平方和为_________。
7、已知数据1,2,3,4,5的方差为2,则11,12,13,14,15的方差为_________,标准差为_______。
8、甲乙两人在相同的条件下各射靶10次,他们的环数的方差是S 甲2
=2.4,•S 乙2
=3.2,则射击稳定性是()A .甲高B .乙高C .两人一样多D .不能确定
9、若一组数据1a ,2a ,…,n a 的方差是5,则一组新数据12a ,22a ,…,n a 2的方差是 A .5B .10 C .20D .50
10、若一组数据1x ,2x ,…,n x 的方差为9,则数据321-x ,322-x ,…,32-n x 的标准
差是_______.
11、某校初三年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计的个数,经统计和计算后结果如下表:
有一位同学根据上面表格得出如下结论:①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班同学比赛成绩的波动比乙班学生比赛成绩的波动大。
上述结论正确的是
12、对甲、乙两同学100米短跑进行5次测试,他们的成绩通过计算得;x&&甲=x&&乙,S2甲=0.025,S2
乙=0.026,下列说法正确的是()
A、甲短跑成绩比乙好
B、乙短跑成绩比甲好
C、甲比乙短跑成绩稳定
D、乙比甲短跑成绩稳定
13、数据70、71、72、73、74的标准差是()A B、2 C、5 4
14、从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)甲:9、10、11、12、7、13、10、8、12、8;
乙:8、13、12、11、10、12、7、7、9、11;
问:(1)哪种农作物的苗长的比较高?
(2)哪种农作物的苗长得比较整齐?。