当前位置：文档之家 › 大学物理A第十章 波函数

大学物理A第十章 波函数

  • 格式：doc
  • 大小：85.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

波函数及其物理意义

波函数及其物理意义
2
A
2 b
(2)求出归一化的波函数和几率密度 几率密度为：
W ( x, t ) ( x, t ) 0
2
2
( x b / 2), x b / 2)
2 2 x W ( x, t ) ( x, t ) cos ( ) (b / 2 x b / 2) b b
结论：自由粒子的物质波是单色平面波。
一个频率为、波长为沿x方向传播的单色平面波 x 的表达式为：
( x, t ) A cos 2 (t
利用波粒二象性的关系式，用描述粒子性的物理 量来代替描述波动性的物理量，有：
3

)
2 ( x, t ) 0 cos ( Et px ) h
P
单缝1使通过它的电 子处于1态；单缝2 使其处于2态。
13
量子力学中态的叠加原理导致了叠加态下观测结果的 不确定性，出现了干涉图样。
它是由微观粒子波粒两象性所决定的。 态迭加原理还有下面的含义：当粒子处于态1和2的 线性迭加态时，粒子是既处于1 ，又处于态2 。
量子力学中态的迭加，虽然在数学上与经典波的迭 加原理相同，但在物理本质上却有根本的不同：量子 态的迭加是指一个粒子的两个态的迭加，其干涉也是 自己与自己的干涉，决不是两个粒子互相干涉。而且 这种态的迭加将导致在迭加态下测量结果的不确定性。
10
2.归一化条件 由于粒子必定要在空间中的某一点出现，所以任 意时刻，在整个空间发现粒子的总几率应是1。所以 2 应有： | | dV 1

V
V | 0 | dV 1
2
这称为波函数的归一化条件。
量子力学中的波函数具有一个独特的性质：波 函数与波函数/=c（c为任意常数）所描写的是 粒子的同一状态。 原因：粒子在空间各点出现的几率只决定于波函数 在空间各点的相对强度，而不决定于强度的绝对大 小。如果把波函数在空间各点的振幅同时增大一倍， 并不影响粒子在空间各点的几率。所以将波函数乘 上一个常数后，所描写的粒子的状态并不改变。 如果波函数对整个空间的积分值是有限的，但不 为零，则可以适当选取波函数的系数，使这积分值 为1，这个过程称为波函数的归一化过程。

大学物理10-2平面简谐波函数

大学物理10-2平面简谐波函数

解: ① 波源振动方程 y
y A cos(t ) 0.04 m
0.4m
o
T /u
0.2m
u P
2 / T 2u / 2 0.08 / 0.4 2 / 5
§2.平面简谐波的波函数 / 四.举例
t
t
=
0
时，o点处的
y 0.04 m
a
b
质点向 y 轴负向
o
运动
/2
y0.2m
u P
波源的振动方程为
y
0.04
cos
2
5
t
2
o
u =0.08 m/s
② 波函数
y
0.04
cos
2
5
t
x 0.08
2
§2.平面简谐波的波函数 / 四.举例
【例题3】如图所示，平面简谐波在 t =0时刻与 t =2s
时刻的波形曲线。求：
（1）坐标原点处介质质点的振动方程；
（2）该波的波动方程。 解：由图的已知量有
o
t
y
A
cos t
x u
y f (x,t)
波函数是波程 x 和时 y
间 t 的函数
o
x
§2.平面简谐波的波函数 / 三.波函数的物理意义
1. 当x一定时，y=y(t)
x=x0,
yxo
(t)
A c os t
x0 u
即 x=x0 处质点的振动方程。 2. 当t一定时，y=y(x)
t=t0
第二节
平面简谐波的 波函数
基本要求
1、掌握简谐波的波函数及其物理意义； 2、能熟练写出简谐波的波动方程； 3、能画波动曲线，并与振动图线相比较。

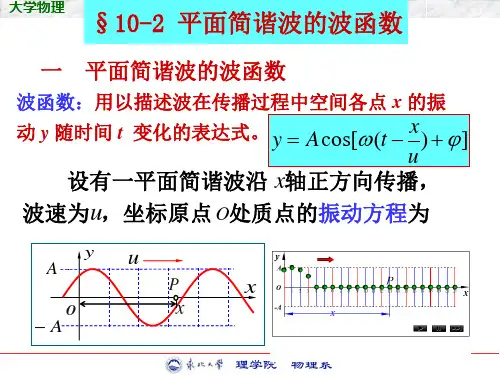
10-2平面简谐波的波函数

10-2平面简谐波的波函数

x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
yO Acost
yO表示质点O在 t时刻离开平衡位置的距离.
考察波线上P点(坐标x), P点比O点的振
动t 落Δ后t 时刻t 的ux,位P移点，在由t此时得刻的位移是O点在
y A
u
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
y
u
A
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
故P点的振动方程（波动方程）为：
y
yo
(t
t)
A cos[ (t
x) u
]
对波动方程的各种形式，应着重从
物理意义上去理解从形式上看：波动是波形的传播.
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
大学物理 §§1100--22 平平面简面谐波简的谐波函波数 的波函数
一 平面简谐波的波函数
波函数：用以描述波在传播过程中空间各点 x 的振
动 y 随时间 t 变化的表达式。 y Acos[(t x) ]
u
设有一平面简谐波沿 x轴正方向传播，
波速为u，坐标原点 O处质点的振动方程为
y A
u
P
uu
Acos[(t x ) ( x0 )]
理学u院 物理u系
大学物理
§10-2 平面简谐波的波函数
例4 一平面简谐波以速度 u 20 m s-1 沿直线传播，波线上点 A 的简谐运动方 程
yA 3102 cos(4 π t); ( y, t单位分别为m，s).

大学物理波函数

大学物理波函数


18
例1:已知描述粒子的归一化波函数为(t,x,y,z)，求在t时刻、 在x到x+dx的无限大薄层内发现粒子的概率。
( t,x ,y ,z ) d x d y d z 解: 体积元内的概率为
Ψ
2
7
4.用电子双缝衍射实验说明概率波的含义 先看经典波： 声波的干涉
振幅矢量相加
i t A ( x ) e 通过上缝的声波用 描述 1 it )e 描述 2(x 通过下缝的声波用 A
A A ) e 双缝 齐开时的声波为 ( 1 2
i t
8
A A ) e 双缝 齐开时的声波为 ( 1 2
薛定谔方程
§15-1 §15-2 §15-3 §15-4 波函数及其统计诠释 薛定谔方程 力学量的算符表示和平均值 一维势阱和势垒问题
1
波函数的统计解释 一、波函数和概率波
二、物理对波函数的要求
三、自由粒子的波函数
2
一、波函数和概率波
1. 波函数
物质波波函数写成 ( r ,t )
2.玻恩（M.Born）假设 物质波不代表实在物理量的波动 而是刻划粒子在空间概率分布的概率波
10
•双缝齐开时 电子可通过上缝 也可通过下缝 通过上 下缝各有一定的概率 总概率幅
Ψ Ψ Ψ 12 1 2
2 12 2 2
21
| Ψ | | Ψ Ψ | 总概率密度 P 12 1
2 1 2 2

12
出现了干涉
干涉项
11
结论 1)干涉是概率波的干涉 是由于概率幅的线性叠加产生的 2)即使只有一个电子 当双缝齐开时
归一化条件
( r , t ) ( r , t ) d 1

大学物理课件：波函数 薛定谔方程

大学物理课件：波函数 薛定谔方程

14.6.2 薛定谔方程
薛定谔方程：适用于低速下微观粒子在力场中运动的 波函数所满足的微分方程称为薛定谔方程. 1.薛定谔方程的建立
a.自由粒子平面波函数：
(x, y,z,t) 0ei[Et(xpx ypy zpz )]/
b.自由粒子的薛定谔方程：
（14.6.4）
2
2 i
2m
t
（14.6.6）
波函数 薛定谔方程 14.6.1 波函数及其统计解释
波函数：由于微观粒子具有波粒二象性，其位置 与动量不能同时确定，所以已无法用经典物理方 法去描述其运动状态，故用波函数描述微观粒子 的运动。
1.经典的波与波函数
机械波：y(x,t) Acos2π(t x )
电磁波：
E ( x,t )
E0
c os 2π(t
c.粒子在外力场中运动且势能为 V
粒子的能量：
E
1 2m
(
px2
py2
pz2
)
V
(x,
y,
z,t)
对应的薛定谔方程：
2
2 V i
2m
t
该方程是关于空间、时间的线性偏微分方程，具有波动 方程的形式。将其应用于微观粒子所得大量结果与实验 符合，薛定谔因此贡献荣获1933年度诺贝尔物理学奖。
2.定态薛定谔方程
例题 14.6.1 设质量为m的粒子沿x轴方向运动，其势
能为：
u(x)
, 0,
x 0,x a 0 x a （14.6.15）
Ep
无限深势阱：该势能如图所示形如一
无限深的阱，故称无限深势阱，本问
题为求解该一维无限深势阱内粒子的
o
ax
波函数。
解：分析 因为势能不随时间变化，故粒子波函数

波函数

波函数
的 能量应等于两个定态的能量差h： En Ek
反子，则吸收光子到高能级去。
31
（2）定态只能是这样的状态，电子饶核公转的动 量矩L等于 h 的整数倍。
2
L n h n n 1,2,3
2
玻尔从经典电磁理论和牛顿运动定律算出氢原子 的定态能量，从而得出氢原子所发的光的频率。
中的电子形成驻波.
28
§3 氢原子
一、原子光谱的实验定律
原子都会发光。原子发的光经过光谱仪后就形成 线状光谱。不同的原子，具有不同的线状光谱。 实验得知：每一种原子都有特定的一系列的光谱项，
个T1光,T谱2 ,项T3的,差。，它所发出的光的波数 ，就是两
Tn Tk n k
n为奇数时
nx A eiknx eiknx
n

2 A cos
kn x

A1
cos
x 2a21
n为偶数时
nx A eiknx eiknx
n
2iA sin kn x A2 sin 2a x
归一化（-a,a)的波函数
nx
1 cos n x
波函数。
d2x dt 2


2
x

0
x Acost
2y 1 2y x2 u2 t 2
y Acos 2 t x
8
当粒子的运动速度远小于光速时，能量E（对自由 粒子，就是动能）和动量P之间的关系：
E p2 2m
i 2 Et px
波函数
1
波函数
对于微观粒子，牛顿方程已不适用，粒子的位 置这一概念是毫无意义的。必需建立能描述微 观粒子运动的基本方程。

大学物理波函数

大学物理波函数

P2

2 a
sin
2
2π a
x
3
E3 9E1
3
2 sin 3π x aa
P3

2 a
sin
2
3π a
x
46
一维无限深方势阱中粒子的波函数和概率密度
电子的相干性注意差别之处10电子的状态用波函数描述?只开上缝时电子有一定的概率通过上缝其状态用描述?只开下缝时电子有一定的概率通过下缝其状态用描述111212干涉项总概率密度电子可通过上缝也可通过下缝通过上下缝各有一定的概率121干涉是概率波的干涉是由于概率幅的线性叠加产生的2即使只有一个电子两部分概率幅的叠加就会产生干涉3微观粒子的波动性实质上就是概率幅的相干叠加性它的状态也要用来描述结论13经典声波干涉项干涉项物质波电子双缝齐开时总的概率幅为1212振幅概率幅14波函数统计诠释量子力学中描述微观粒子的波函数本身是没有直接物理意义的具有直接物理意义的是波函数的模的平方它代表了粒子出现的概率
概率密度为 (x, y, z, t) (x, y, z, t) (x, y, z, t)
波函数是单值的、连续的和有限的。
波函数 (r,t)和A (r,t) (A是常数)描述了同一个量子 态，对于空间任意两点 ri 和 rj 有
(ri ,t) 2

(rj
,
t
)
2

写成
i
t


2 2m
2 x 2
•令上述关系作用于波函数 (x,t)
•得到自由粒子满足的薛定谔方程
i (x,t) 2 2 (x, t)
t
2m x2
23
3. 有势场中粒子的薛定谔方程

波函数PPT课件

波函数PPT课件
什么是波包？波包是各种波数（长）平面波的迭加。
平面波描写自由粒子，其特点是充满整个空间，这是因为平面波 振幅与位置无关。如果粒子由波组成，那么自由粒子将充满整个空间， 这是没有意义的，与实验事实相矛盾。
实验上观测到的电子，总是处于一个小区域内。例如在一个原子内，其 广延不会超过原子大小≈1 Å 。
)
x
(ax) 1 ( x)
|a|
f ( x) ( x x0 )
f
(
x0
)
(
x
x0
)
.
作代换：px x，px x0，则
(
px
px )
1
2
e dx i (
p
x
px
)
x
14
II 平面波 归一化
p(r , t )
i[
Ae
p•r Et ]
p
(r )e
i
Et
t=0 时的平面波
写成分量形式
Q光
屏
Q
6
结论：衍射实验所揭示的电子的波动性是： 许多电子在同一个实验中的统计结果，或者是一个
电子在许多次相同实验中的统计结果。
波函数正是为了描述粒子的这种行为而引进的，在此基
础上，Born 提出了波函数意义的统计解释。
在电子衍射实验中，照相底片上
r 点附近衍射花样的强度
正比于该点附近感光点的数目， 正比于该点附近出现的电子数目， 正比于电子出现在 r 点附近的几率。
.
12
（4）平面波归一化 I Dirac —函数
定义：
0 ( x x0 )
x x0 x x0
x0 x0
(x
x0 )dx
( x x0 )dx 1

大学物理 平面简谐波的波函数

大学物理 平面简谐波的波函数
此刻的波形.
y Acos[2 π x (2π t )] T
y(x,t) y(x ,t)（波具有空间的周期性）
波程差
x21 x2 x1
12
1 2
2π
x2 x1
2π
x21
2π
x
回目录
3若
x, t 均变化，波函数表示波形沿传播方向的运动情况（行波）.
yu
t 时刻
x
O
x
t t 时刻
xx
x 0.5处m质点的振动方程
y 1.0cos(π t π)m
y
y/m
3
1.0
3*
2
4
4O
2
0
* 1.0
* 2.0
*
t /s
1 -1.0* 1
*
x 0.5 m 处质点的振动曲线
回目录
例2 一平面简谐波以速度
沿u直线传20播m,波线/ s上点 A 的简谐运动方
程
. yA 310 2 cos(4 π t)m
y Acos式(中Bt Cx)
A, B, C 为正常数，求波长、波速、波传播方向上相距为 的两点间的相位差.
d
y Acos(Bt Cx)
y Acos2 π ( t x )
T
2π
C
T 2π B
u B
TC
2π d dC回目录
二 波函数的物理意义
y Acos[(t x) ] Acos[2 π( t x ) ]
u
8m 5m 9m
C
B oA
Dx
1）以 A 为坐标原点，写出波函数
两种方法：时间推迟法和相位落后法
y 3102 cos[4 π(t x )]m 20

大一物理波函数知识点

大一物理波函数知识点

大一物理波函数知识点波函数是描述处于量子力学状态的粒子的数学函数。

在物理学中，波函数是一种表示粒子位置和能量状态的数学函数，它可以用来预测粒子在空间中的位置和运动状态。

在大一物理学中，学生需要掌握一些关键的波函数知识点，以理解和解决与波函数相关的问题。

本文将介绍几个在大一物理课程中常见的波函数知识点。

1. 波函数的定义和性质在量子力学中，波函数通常用符号ψ表示。

波函数是一个复数函数，其绝对值的平方表示了粒子在各个位置出现的概率密度。

波函数必须满足归一化条件，即波函数的平方在整个空间积分等于1。

波函数还必须是连续且可导的，并且在无穷远处趋于零，以保证物理意义上的可行性。

2. 波函数的时间依赖性波函数的时间演化由薛定谔方程描述。

根据薛定谔方程，波函数随时间的演化由一个时间项决定。

这个时间项通常表示为一个复数指数函数，其中包含了粒子的能量和时间。

通过求解时间演化的薛定谔方程，我们可以获得粒子随时间的行为和定态的波函数。

3. 波函数的定态和本征态定态波函数是指不随时间变化的波函数，它们对应于粒子的定态能量和定态位置。

对于定态波函数，它们的时间项为常数，通常表示为e^(-iEt/ħ)，其中E代表粒子的能量，ħ是普朗克常数除以2π。

与定态波函数相关联的能量称为本征能量，而定态波函数本身称为本征态。

4. 波函数和测量根据量子力学的测量原理，测量粒子的某个物理量会导致波函数的坍缩，使其变为特定的态。

例如，在进行位置测量时，波函数将坍缩为表示粒子处于特定位置的本征态。

这种波函数坍缩的概率由波函数在各个位置的概率密度确定。

波函数坍缩后，我们可以得到特定位置的测量结果。

5. 波函数的叠加和干涉波函数存在叠加和干涉的现象。

叠加指的是当存在多个可能状态时，波函数可以表示为这些状态的线性组合。

例如，一个粒子既可以处于位置A，也可以处于位置B，那么粒子的波函数可以表示为ψ = αψ_A + βψ_B，其中α和β是复数系数。

当这些状态存在相位差时，波函数还会发生干涉现象，导致一些位置的概率密度增强或减弱。

大学物理平面简谐波的波函数精选精品文档

大学物理平面简谐波的波函数精选精品文档

u
1m 0
λ10m 8 m 5 m 9 m
C
B oA
Dx
第十章 波动
21
物理学
第五版
选择进入下一节：
本章目录
6-1 机械波的几个概念
6-2 平面简谐波的波函数
6-3 波的能量 能流密度 6-4 惠更斯原理 波的衍射和干涉
6-5 驻波
6-6 多普勒效应
第十章 波动
22

x






A cos


t

2πx




第十章 波动
4
物理学
第五版
6-2 平面简谐波的波函数
波函数
yAcos(t[x)]
u
质点的振动速度，加速度
v y A si n (t [x)]
t
u
a 2 t2 y 2A co (ts[u x)]
第五版
6-2 平面简谐波的波函数
(3) x0.5m处质点的振动规律并作图
y1.0co2π s([t x)π] 2.0 2.0 2
x0.5m处质点的振动方程
ycoπst[π](m)
y
y/m
3
3
1.0
*
4O
2
0 2* 1.0 *4 2.0 * t / s
1 -1.0*1
*
x0.5m处质点的振动曲线
第十章 波动
15
物理学
第五版
6-2 平面简谐波的波函数
例2 一平面简谐波以速度u20ms-1
沿直线传播，波线上点 A 的简谐运动方 程
yA31 0 2co4π st)(; ( y, t单位分别为m，s).

大学本科大学物理第5次课 波函数

大学本科大学物理第5次课 波函数

os2π
t T
x
A c ost
2πx
第十章 波动
5
物理学
第五版
10-6 多普勒效应
波函数
y Acos[(t x) ]
u
质点的振动速度，加速度
v y Asin[(t x) ]
t
u
a
2 y t 2
2
A cos[ (t
x) u
]
第十章 波动
6
物理学
第五版
10-6 多普勒效应
二 波函数的物理含义
y
y/m
3
3
1.0
*
4O
2
0 2* 1.0 *4 2.0 * t / s
1 -1.0*1
*
x 0.5 m 处质点的振动曲线
第十章 波动
16
物理学
第五版
10-6 多普勒效应
例2 一平面简谐波以速度u 20 m s-1
沿直线传播，波线上点 A 的简谐运动方 程
yA 3102 cos(4 π t); ( y, t单位分别为m，s).
yu
O
x
第十章 波动
10
物理学
第五版
10-6 多普勒效应
4 沿 x轴方向传播的波动方程
如图，设 O 点振动方程为
yO A cost
P点振动比O点超前了 Δt x u
y
u
A
P
x
O
x
A
第十章 波动
11
物理学
第五版
10-6 多普勒效应
故P点的振动方程（波动方程）为：
y
yo (t
t)
A c os [ (t
点C 的相位比点A 超前

大学物理A第十章 波函数

大学物理A第十章 波函数

第十章 波函数一、填空题（每空3分）10-1 A,B 是简谐波同一波线上两点，已知B 点的相位比A 点超前2π，且波长4m λ=，波速2u m s =，则两点相距 ，频率为 。

(1,12m Hz )10-2 A,B 是简谐波同一波线上两点，已知B 点的相位比A 点超前2π，且波长4m λ=，波速2u m s =，则两点相距 。

(1m )10-3 一列横波沿X 正向传播，波速u=1m/s,波长λ=2m,已知在X=0.5m 处振动表达式为Y=2cos πt(SI),则其波函数为_______.( y=2cos(πt-πx+2π) （SI ）) 10-4波源位于x 轴的坐标原点，运动方程为t y π240cos 100.43-⨯=，式中y 的单位为m ，t的单位为s ，它所形成的波形以 1s m 30-⋅ 的速度沿x 轴正向传播，则其波动方程为___ _____。

（))(8240cos(100.43m x t y ππ-⨯=-）10-5机械波的表达式为()()0.05cos 60.06y t x m ππ=+，则该波的周期为 。

(13s ) 10-6一平面简谐波的波动方程为)2 4cos(08.0x t y ππ-=，式中单位为SI 制 。

则：（1）对于某一平衡位置，2=t s 与1.2=t s 时的相位差为 ；（2）对于同一时刻，离波源0.80 m 及0.30 m 两处的相位差为 。

（0.4π；π）10-7 一列横波在x 轴线上沿正向传播，在t 1＝0和t 2＝0.5s 时波形如图所示，设周期12t t T ->，波动方程为 。

()42cos(2.0xt y πππ-+=)10-8 某波线上有相距2.5cm 的A 、B 两点，已知振动周期为2.0s ，B 点的振动落后于A 点的相位为π/6，则波长λ = ，波速u = 。

（λ=0.3m ，u=0.15m/s ） 10-9一横波沿x 轴正向传播,波速u = 1m/s, ,已知在 x = 0.5m 处振动表达式为t yπcos 5=(SI) ,o242.0m y /mx /01=t s 5.02=t则其波函数为___ 。

波函数

波函数
x P 点振动比O点超前了 Δt u
A
y
O
u
P x
x
A
第十章 波动
11
物理学
第五版
10-6
多普勒效应
故P点的振动方程（波动方程）为：
x y yo (t t ) A cos[ (t ) ] u
对波动方程的各种形式，应着重从 物理意义上去理解和把握. 从实质上看：波动是振动的传播.
(3) x 0.5 m 处质点的振动规律并作图. 解 (1) 写出波动方程的标准式 t x y A cos[ 2π ( ) ] T
第十章 波动
13
物理学
第五版
10-6
多普勒效应
t x y A cos[ 2π ( ) ] T
t 0 x0
π y y 0, v 0 2 t t x π y cos[ 2 π ( ) ] (m) 2.0 2.0 2
2 1
2
1
AC

]
410 πs u y A (3 10 m) cos( m )t 8m 5m 9m
C B
2
1
oA
D
x
20
第十章 波动
物理学
第五版
10-6
多普勒效应
点 D 的相位落后于点 A
AD y D (3 10 m)cos[4 s ]t 2 λ 9 2 1 (3 10 m) cos[( 4 π s )t π] 5
y
o
第十章 波动
x
9
物理学
第五版
10-6
多普勒效应
3 x 、 t 都变 方程表示在不同时刻各质点的位移， 即不同时刻的波形，体现了波的传播.

大学物理 平面简谐波的波函数

大学物理 平面简谐波的波函数

17
3）写出传播方向上点C、点D 的简谐运动方程
u
C
8m
y A 310 cos( 4 π t )m 10m 5m 9m
B
2
oA
D
x
AC
点 C 的相位比点 A 超前
cos( 4 π t 2 π )m 13 2 3 10 cos( 4 π t π)m 5 点 D 的相位落后于点 A AD 2 y D 3 10 cos( 4 π t 2 π )m 9 2 3 10 cos( 4 π t π)m 5
4
波动方程的其它形式
t x y ( x,t ) A cos[ 2 π( ) ] T λ y( x, t ) A cos(t kx )
质点的振动速度，加速度 角波数 k 2 π
(wave number)

y x v A sin[ (t ) ] t u
分析：
2 3 ( D) 2
( B)

,
由波形图可判定O点在该时刻的振动方向竖直向 上（如图示）
A x
3 由旋转矢量图可知此时的相位为 2
23
3.在下面几种说法中,正确的说法是: （C）
(A)波源不动时,波源的振动周期与波动的周期在数 值上是不同的。 (B)在波传播方向上的任一质点振动位相总是比波源 的位相超前。 (C)在波传播方向上的任一质点振动位相总是比波源 的位相滞后。 (D) 波源的振动速度与波速相同。
在t＝1／v时刻：
1 v | x x2 2A sin 2 (1 ) 2A 4
即速度比为-1。
3 v | x x1 2A sin 2 (1 ) 2A 4

大学物理(下册) 10.3平面简谐波的波函数

大学物理(下册) 10.3平面简谐波的波函数

y A cos(t )
2 1 A 0.2m ， T 2s ， π s 。 由图10.7可知： T
π 0 0.2cos ， 将初始条件代入振动方程可得： 2 由旋转矢量法得 t 0 y 0 处质点的速度大于零,既有：
π y 0.2cos( t ) 2 2
各质点相对平衡 位置位移
(1)
波线上各质点 平衡位置
波函数：介质中坐标为 x 的质点相对其平衡位置的位 移 y 随 t 的变化关系 y ( x, t ) 称为波函数；
二、平面简谐波波函数的建立
设：平面简谐波以速度u 沿 x 轴正向传播；
导出简谐波的波函数： 时间推迟法；
波源：设位于原点O 的质点作初相为零的谐振动；
振动方程： yO A cos t
(2)
问题：由于该质点的振动及弹性介质，使 x 轴上其 它质点产生振动，它们的振动方程 如何？
选择x 轴上距波源 O 点为 x 的 P点 作 为 研 究象，当振动传到 P 点时，该质点以相 同的振幅、频率重复O点振动，但时间上落后：
x t u
即点P的振动相位落后O点：
x (t ) u
(3)
(4)
于是点P 的振动可表示为：
x y P A cos (t ) u
(5)
P 点是任选的，故上式对 x 轴上任意一点均成立：
故得沿 x 轴正向传播的平面简谐波波函数：
x y A cos (t ) u
(6)
A
若原点初相不为零：
y
u

x
x 0， 0
，
(2)由相位落后法知，任意点处质点 的振动相位落后原点处质点的相 位，故波函数为：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十章波函数一、填空题(每空3分）１0—1 A,B就是简谐波同一波线上两点,已知B点得相位比A点超前，且波长，波速,则两点相距 ,频率为。

()10—2 A，B就是简谐波同一波线上两点,已知B点得相位比A点超前，且波长,波速，则两点相距 .（1m ）１０—3 一列横波沿X正向传播，波速u＝1m／ｓ，波长λ=2m，已知在X=0.5m处振动表达式为Y=２cos t（SI),则其波函数为_＿_＿___、（ｙ=2coｓ（t-x+） (SI)) １0—4波源位于ｘ轴得坐标原点，运动方程为,式中y得单位为m,t得单位为s，它所形成得波形以得速度沿ｘ轴正向传播，则其波动方程为___ ＿____。

（）10—5机械波得表达式为，则该波得周期为。

（）10-6一平面简谐波得波动方程为，式中单位为ＳI制。

则:（１）对于某一平衡位置,s与ｓ时得相位差为;(2)对于同一时刻，离波源０。

８０ｍ及0.３0m两处得相位差为.（0、4π;π)１0—7 一列横波在ｘ轴线上沿正向传播,在ｔ1=0与t２=0、5ｓ时波形如图所示，设周期，波动方程为.（）10-８某波线上有相距2．5ｃm得A、B两点，已知振动周期为2、0ｓ,B点得振动落后于A点得相位为π/6，则波长λ= ,波速u= 。

(λ＝0.３ｍ,ｕ=０。

15m/s) １0-９一横波沿ｘ轴正向传播，波速u = 1m／ｓ, ，已知在x ＝０．5m处振动表达式为（S Ｉ），则其波函数为___。

（）1０—10两波相干得充要条件就是 .（频率相同、振动方向平行、相位相同或有恒定得相位差.)１0－1１一简谐波沿X轴正向传播，λ = 4m，T =已知点得振动曲线如图所示,点得振动方程为_＿__________＿_＿_____，波函数为_＿__＿_______＿_＿___＿___＿_＿＿_（, )１0－12 为两相干波源，其振幅相等，并发出波长为得简谐波，P点就是两列波相遇区域中得一点，距离如图所示， 得振动方程为 , 若只有波源时，s １ 、p 间得相位差为＿＿_____，当同时存在时,若P 点处发生相消干涉时，得振动方程为__＿_____＿_、(4π, 或）10－13 一平面简谐波以速度 ｕ = 20 ｍ / ｓ 沿直线传播,已知在传播路径上某点 A 得简谐运动方程为其频率，C Ｄ 两点得相位差为__＿＿_＿_____、（, ）10-１4 已知位于x 轴坐标原点处得波源作振幅为A 、周期为0、0２ｓ得振动，若振动以得速度沿ｘ轴正向传播，设时波源处得质点经平衡位置向正方向运动,则其波动方程为＿_____＿＿_.（）１0－15 在波长为λ得驻波中,相邻得波腹与波节之间得距离为_＿___＿__＿。

（）10－16 在波长为λ得驻波中,两个相邻得波腹之间得距离为_________。

() *u x二、选择题（每小题3分）10—17 简谐波传播过程中，沿传播方向相距半个波长得两点,同一时刻该两点得振动位移必定( A )(A)大小相等，而方向相反；（B)大小与方向均相等;(Ｃ)大小不同,方向相同； (Ｄ)大小不同，而方向相反。

10—18 械波得表达式为则( C )(Ａ)波长为; (Ｂ)波速为；(C）周期为； (D）波沿轴正方向传播。

10-1９在下面几种说法中，正确得就是（ C )。

（Ａ）机械振动一定能产生机械波;（Ｂ) 质点得振动速度与波得传播速度就是相等得；(C）质点得振动周期与波得振动周期就是相等得；（D) 波动方程中得坐标原点一定选取在波源位置.10—２0在简谐波传播过程中,沿传播方向相距为(为波长）得两点得振动速度必定（Ａ）A 大小相等，而方向相反、 B 大小与方向均相等、C大小不同，方向相同、D大小不同，而方向相反、10-21 下面说法正确得就是（ C ）（Ａ)波源不动时，波源得振动周期与波动得周期在数值上就是不同得；（B)波源振动得速度与波速相同；（C)在波传播方向上,任一质点得振动相位总就是比波源得相位滞后;（D）在波传播方向上,任一质点得振动相位总就是比波源得相位超前.10－２2一平面简谐波得方程为,在时刻，与两点处介质质点速度之比就是（ B )（A）；（B）；（Ｃ）； (Ｄ).10－23一平面简谐波沿x轴正向传播,已知振幅Ａ、周期为T、波长为λ，在t＝０时,x = 0处得质点位于y得正方向得最大位移处(题中单位采用ＳＩ制)，则波得表达式为:( D ) (A）m; (Ｂ) ｍ;（Ｃ）m ; （D）m 。

1０-２４在波长为λ得驻波中,两个相邻得波腹之间得距离( B ）（A)；（Ｂ)；(C); （D）.10-25 一平面简谐波沿x轴负向传播,已知振幅A、角频率ω、波速u ,在ｔ= 0时,ｘ=０处得质点位于平衡位置，且向位移(ｙ)得正方向运动,则波得表达式为：( B)（Ａ)m ；（Ｂ) ｍ;（Ｃ）m ; (Ｄ）m。

1０-26 一平面简谐波得波动方程为y＝Aｃos(Bt Ｃｘ）,式中A，B,C为正值恒量，则( Ｄ)（A)波速为Ｃ；（B)周期为１/B；（C）波长为C/2 ; （D）角频率为B。

1０—27下面几种说法中，正确得就是:( C)(A)波源振动得速度与波速相同；（B）当波从一种介质进入另一种介质时，波速不会改变。

（C)当波从一种介质进入另一种介质时，频率不会改变。

(D)当波从一种介质进入另一种介质时,波长不会改变.10—28一平面简谐波沿x轴正向传播,波长为λ,已知处质点得振动方程为，其波动方程为( B ）(A) （Ｂ)(Ｃ）（D)10-29 一平面简谐波在弹性媒质中传播时，在传播方向上媒质中某质元在负得最大位移处,则它得（Ｂ）(A）动能为零，势能最大（Ｂ）动能为零，势能为零（C)动能最大，势能最大 (D）动能最大,势能为零10—３0图(a)表示t=0时简谐波得波形图，波沿x轴负方向传播，图（ｂ）为一质点得振动曲线.则图（a)所表示得x ＝0处振动得初相位与图（b)所表示得振动得初相位分别为（C）(10—31（（Ｂ）；（C)；（Ｄ）。

１0－32如图所示,Ｐ点相遇,波在点S1振动得初相位就是,点S1点得距离就是，波在点S2振动得初相位就是,点S2到Ｐ点得距离就是，以k代表零或正、负整数，则点P就是干涉极大值得条件为( D）(Ａ)；（B)；(C）；（D)S2S1Pr2r1三、计算题(共40分）10-3３一平面简谐波在传播路径上有A、B两点，B点得振动相位比A点落后已知AB之间得距离为,振动周期为2s,试求：(1)波长与波速;（2）若时刻，A点正位于且向正方向运动（为振幅,），试以B点为坐标原点，波传播方向为轴正向，写出波函数。

１0—34(本题1０分)一平面简谐波在传播路径上有A、Ｂ两点，B点得振动相位比Ａ点落后已知AB之间得距离为,振动周期为２s,试求:(１）波长与波速；（２)若时刻,A点正位于且向正方向运动(为振幅，），试以B点为坐标原点,波传播方向为轴负向，写出波函数。

10－35 频率为得声波以得速度沿某一波线传播,先经过波线上得A点,再传到B点，设,试求：(1）同一时刻A、B两点振动得相位差。

（2）同一振动状态从A传播到B点所需得时间.10-３6 (１0分)图为t=０时,平面简谐波得波形图，波速u＝8ｍｍ/s求（1）原点O得振动方程;（2）波动方程；(3）X=3m处质点得振动方程、２ 3 ４10-3７一平面简谐波在时刻得波形如图所示,设波得频率为，且此时图中P点得运动方向向上,求（１）此波得波函数；（2）P点得振动方程。

10-38 两相干波源分别在P、Q干波，R为PQ连线上得一点.得初相位；(2）两波源初相位差为.设两波在P解:设,两波源P,Q得初相位分别为1０—39 一波源作简谐振动,周期为，振幅为，以波源经平衡位置向正方向运动时作为计时起点。

设此振动以得速度沿直线传播，以波源处为原点,波传播方向为轴正方向。

试写出波函数。

10-40图为平面简谐波在t＝０时刻得波形图，设此简谐波得频率为250Hｚ,且此时图中质点P 得运动方向向上。

求：（1)该波得波动方程；（2)在坐标轴正向距原点O为5m 处质点得运动方程与t＝０时该点得振动速度。

（1０分）【解】（１）O点得振动方程 (3分）波动方程(2分)（2）（2分）时（3分)10-41两相干波源位于同一介质中得A、B 两点,其振幅相等、频率皆为100Hz，B比Ａ得相位超前 。

若A、B相距30.0m ，波速为ｕ＝400m/s ,试求AB 连线上因干涉而静止得各点得位置.(１０分)解：(2分)位于点A外侧部分（2分)位于点B外侧部分(2分）以上两区域均无干涉静止点位于点Ａ、B中间部分(2分) 干涉静止得点满足方程即干涉静止得点距A 端 1，３,…29m （2分）10－42 如图所示，A、Ｂ两点为同一介质中两相干波源,其振幅为5cm，频率皆为1００H z,但当点A为波峰时,点 B 适为波谷，设波速为10m/s ,试求A、Ｂ发出得两列波传到点P 时得相位差及干涉得结果.(10分)【解】（2分)(２分）（３分)两波传到Ｐ点处相位差为π得奇数倍,故在Ｐ点干涉相消。

（3分）10－4３ 沿x 轴正向传播得波，波速为２m/s,波源得振动方程为Y=０、１cos t （SI),介质无吸收、求：（１）波得振幅、频率、周期、波长；（2)波动方程；（3）同一时刻在距原点分别为1米、1.5米得两点得相位差、解：（1） (１分） （２分）（1分) (１分）(2） 波动方程为 ｍ （3分）（３） （2分）10－44 图为平面简谐波在t = 0 时刻得波形图，此简谐波以速度沿ｘ轴正向传播。

求:（1）该波得波动方程;（２）ｍ处质点P 得运动方程. (1０分）解：(1) (2分）(2分）波动方程（3分)(2）处得Ｐ点得振动方程为10—4５ 图所示为处质点得振动曲线，求此波得波动方程、（10分）【解】由题意知质点振动得振幅A=０。

4ｍ,处得质点在A/2 处并向Oy 轴正向移动(1作出旋转矢量图,可得初相位 （2分)当质点第一次回到平衡位置，由得 (2分）所以在处得运动方程为 （2分)波动方程得标准形式为：其中及带入上式，比较可得即得 （2分）所以波动方程为(１分）。