第三章 平面连杆机构及其设计-样稿-李瑞琴汇编

第三章 平面连杆机构及其设计内容提要：本章以平面四杆机构的运动学特性和综合为主线。

其主要内容有：介绍平面连杆机构的特点和应用；阐明平面连杆机构的基本类型及其演化方法；探讨平面连杆机构的运动特性，重点探讨平面四杆机构的设计的图解法及解析法；给出平面连杆机构的计算机辅助设计的流程及实例；拓展阅读部分介绍平面多杆机构的设计。

§3.1 平面连杆机构的类型和应用3.1.1 平面连杆机构的特点连杆机构是由低副将若干构件联接而成的，故又称为低副机构。

连杆机构可根据其构件之间的相对运动是平面运动还是空间运动，分为平面连杆机构和空间连杆机构；又可根据机构中构件数目的多少分为五杆机构、六杆机构等。

一般将五个或五个以上的构件组成的连杆机构称为多杆机构。

单闭环的平面连杆机构的构件数至少为4，因而没有平面三杆机构；单闭环的空间连杆机构的构件数至少为3，因而可由三个构件组成空间三杆机构。

平面连杆机构是若干个构件用平面低副(转动副、移动副)连接而成，各构件在相互平行的平面内运动，又称为平面低副机构。

由于平面连杆机构能够实现多种运动轨迹曲线和运动规律，且低副不易磨损而又易于加工，以及能由本身几何形状保持接触等特点，因此广泛应用于各种机械及仪表中。

平面连杆机构的不足之处主要有两点，其一是连杆机构中作变速运动的构件惯性力及惯性力矩难以完全平衡；其二是连杆机构较难准确实现任意预期的运动规律，设计方法较复杂。

连杆机构中应用最广泛的是平面四杆机构，它是构成和研究平面多杆机构的基础。

本章主要讨论平面四杆机构及其运动设计问题。

3.1.2 平面四杆机构的基本型式如图3.1所示，所有运动副均为转动副的平面四杆机构称为铰链四杆机构，它是平面四杆机构的基本型式。

其它型式的四杆机构都可以看成是在它的基础上通过演变而成的。

在此机构中，构件4称为机架，与机架以运动副相联的构件1和构件3称为连架杆。

在连架杆中，能绕其轴线回转360° 者称为曲柄；仅能绕其轴线往复摆动的，称为摇杆。

不与机架相连的构件2作平面复杂运动，称为连杆。

按照两连架杆运动形式的不同，可将铰链四杆机构分为三种基本型式。

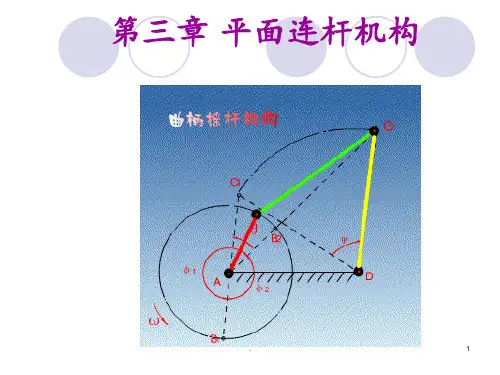
1．曲柄摇杆机构（Crank-rocker mechanism ）图3.1 铰链四杆机构的基本型式3连架杆2在铰链四杆机构中，若两连架杆中有一个为曲柄，另一个为摇杆，则称为曲柄摇杆机构。

图3.2所示的调整雷达天线俯仰角的机构和图3.3所示的电影放映机拉片机构均是曲柄摇杆机构的应用实例。

2．双曲柄机构（Double-crank mechanism ）两连架杆均为曲柄的机构称为双曲柄机构。

在双曲柄机构中，若两组对边的构件长度相等，则可得如图3.4（a ）所示的平行四边形机构和图3.4（b ）所示的反平行四边形机构。

平形四边形机构的特点是：两曲柄的回转方向相同，且角速度时时相等，连杆作平动。

平行四边形机构有一个位置不确定的问题，如图3.5中的位置2C ，2C 所示。

为解决此问题，可以在从动曲柄CD 上加装一个惯性较大的轮子，利用惯性维持从动曲柄转向不变。

也可以通过加虚约束使机构保持平行四边形，如图3.6所示的机车车轮联动的平行四边形机构，从而避免机构运动的不确定性。

反向平行四边形机构中的两曲柄回转方向相反，且角速度不等。

图3.7所示的汽车车门启闭机构即为其应用实例。

图3.4 双曲柄机构C（a ）平行四边形机构（b ）反平行四边形机构图3.7 汽车车门启闭机构3．双摇杆机构(Double-rocker mechanism)在铰链四杆机构中，若两连架杆均为摇杆，则称为双摇杆机构。

图3.8所示的鹤式起重机中的四杆机构ABCD 即为双摇杆机构，当主动摇杆AB 摆动时，从动摇杆CD 也随之摆动，位于连杆CB 延长线上的重物悬挂点E 将近似沿水平方向作直线移动。

B 1C 2AB C D EF 1 2345图3.6 机车车轮联动机构图3.5 平行四边形机构的位置不确定性A BCD2C C 1 C 2B 1B 21 234C'B'CE BE'DQ QA图3.8 鹤式起重机中的双摇杆机构3.1.2 平面四杆机构的演化除了上述铰链四杆机构外，工程实际中还广泛应用着其它类型的四杆机构，这些四杆机构都可以看作是由铰链四杆机构通过不同的方法演化而来的，掌握这些演化方法，有利于对平面连杆机构进行创新设计。

下面介绍一些常用的演化方法。

1．转动副转化成移动副4在图3.9（a ）所示的曲柄摇杆机构中，摇杆3上的点C 的运动轨迹是以D 为圆心，以摇杆长CD l 为半径所作的圆弧。

若将构件3改为滑块，使其在以D 点为圆心，以CD l 为半径的弧形槽中运动，则机构的运动特性完全一样，此时机构演化成图3.9（b ）所示的具有弧形滑道的连杆机构。

若此弧形槽的半径增至无穷大，则弧形槽变成直槽，转动副也就转化成移动副，构件3也就由摇杆变成了滑块，这样，曲柄摇杆机构就演化成了图3.9（c ）所示的曲柄滑块机构。

该机构中滑块3上的转动副中心在定参考系中的移动方位线不通过连架杆1的回转中心，称为偏置曲柄滑块机构。

图中e 为连架杆转动中心至滑块上转动副中心的移动方位线的垂直距离，称为偏距。

若偏距0e =，则滑块上的转动副中心移动方位线通过曲柄回转中心，称为对心曲柄滑块机构，如图3.9（d ）所示。

（a ）α（b ）图3.9 一个转动副转化成移动副（a ）曲柄摇杆机构（b ）曲线导轨曲柄滑块机构（d ）对心曲柄滑块机构（c ）偏置曲柄滑块机构6如图3.10（a ）所示，将对心曲柄滑块机构中的连杆2变换成滑块，滑块3变换成具有半径为BC l 弧形槽的移动构件，则机构的运动特性不变，得到图3.10（b ）所示的机构形式。

若弧形槽的半径BC l 趋于无穷远，则对心曲柄滑块机构演化成具有两个移动副的机构，如图3.10（c ）所示。

该机构具有如下几何尺寸关系：sin AB s l ϕ=。

因此，该机构也称为正弦机构。

缝纫机的引线机构就是一正弦机构。

进行类似的变换，可在曲柄滑块机构的基础上，将转动副A 演变成移动副，得到如图3.11所示的双滑块机构。

图3.12所示的椭圆仪机构是双滑块机构的应用实例；也可将转动副B 演变成移动副，得到图3.13所示的正切机构，该机构的几何尺寸满足正切关系：tan y L ϕ=。

图3.12 椭圆仪机构 2．选取不同的构件为机架低副机构具有运动的可逆性，即无论取哪一个构件为机架，机构各构件间的相对运动关系不变。

但选取不同构件为机架时，却可得到不同型式的机构。

这种采用不同构件为机架的演变方式称为机构的倒置。

如表3.1所示，对于曲柄摇杆机构，选取不同的构件为机架时，可得到双曲柄机构、双摇杆机构和另一个曲柄摇杆机构。

习惯上称后三种机构为第一种机构的倒置机构。

对于曲柄滑块机构，当选取不同的构件为机架时，可得到具有一个移动副的几种四杆机构。

当杆状构件与块状构件组成移动副时，若杆状构件为机架，则称其为导路；若杆状构件作整周转动，则称其为转动导杆；若杆状构件作非整周转动，则称其为摆动导杆；若杆状构件作移动，则称其为移动导杆。

对于具有两个移动副的双滑块机构，当取不同构件为机架时，可得到四种不同型式的四杆机构。

图3.11 双滑块机构图3.13 正切机构图3.10 两个转动副转化成移动副3．扩大转动副的尺寸在图3.14（a ）所示的曲柄摇杆机构中，如果将曲柄1端部的转动副B 的半径加大至超过曲柄1的长度AB l ，便可得到如图3.14（b ）所示的偏心轮机构。

此时，曲柄1变成了一个几何中心为B ，回转中心为A 的偏心圆盘，其偏心距e 为原曲柄长。

该机构与原曲柄摇杆机构的运动特性完全相同。

在设计机构时，当曲柄长度很短、曲柄销需承受较大冲击载荷而工作行程很小时，常采用这种偏心圆盘结构型式，在冲床、剪床、压印机床、柱塞油泵等设备中，均可见到这种机构。

图3.14 偏心圆盘机构（a ）（b ）表3.1四杆机构的几种演化型式§3.2 平面连杆机构的运动特性和传力特性平面连杆机构具有传递和变换运动，以及实现力的传递和变换的功能，前者称为平面连杆机构的运动特性，后者称为平面连杆机构的传力特性。

了解这些特性，对于正确选择平面连杆机构的类型，进而进行机构设计具有重要意义。

3.2.1 平面四杆机构有曲柄的条件平面铰链四杆机构有三种基本型式：曲柄摇杆机构（一个曲柄）、双曲柄机构（二个曲柄）和双摇杆机构（没有曲柄）。

可见有没有曲柄，有几个曲柄是铰链四杆机构基本型式的主要特征。

因此，曲柄存在条件在连杆机构设计中具有十分重要的地位。

下面以图3.15所示的铰链四杆机构为例分析曲柄存在的条件。

设AB a =，BC b =，CD c =，AD d =设d a >，在杆1绕转动副A 转动的过程中，铰链点B 与D 之间的距离是不断变化的。

如果杆1能绕转动副A 作整周转动，则杆1应能通过1AB 和2AB 这两个关键位置，即连架杆1与机架4拉直共线的位置和重叠共线的位置。

根据这两个位置构成的三角形11B C D 和三角形22B C D 中的杆长关系可推出以下各式：由11B C D ∆可得： a d b c ++≤ （a ）由22B C D ∆可得： ()b c d a +-≤ → a b c d ++≤ （b ） 和 ()c b d a +-≤ → a c b d ++≤ （c ）将式（a ），（b ），（c ）分别两两相加得：a ba c a d ⎧⎪⎨⎪⎩≤≤≤ （3.1） 如果d a <，用同样的方法可以得到杆1能绕转动副A 相对于杆4作整周转动的条件为：ABCD B 1B 2C 1C 2123 4 图3.15 平面四杆机构的有曲柄条件10d a b c ++≤ （d ）d b a c ++≤ （e ） d c a b ++≤ （f ）d a d b d c ⎧⎪⎨⎪⎩≤≤≤ （3.2） 式（3.1）和式（3.2）说明组成整转副A 的两构件中，必有一杆为最短杆；式（a ），（b ），（c ）和式（d ），（e ），（f ）说明，该最短杆与最长杆杆长之和小于或等于其它两杆长度之和，该长度之和关系称为“杆长和条件”。

综合以上两种情况，可以得出以下重要结论：在铰链四杆机构中，如果某个转动副能成为整转副，则它所连接的两个构件中，必有一个为最短杆，并且四个构件的长度关系满足杆长和条件。

在有整转副存在的铰链四杆机构中，最短杆两端的转动副均为整转副。

此时，若取最短杆为机架，则得双曲柄机构；若取最短杆的任一邻边构件为机架，则得曲柄摇杆机构；若取最短杆的对边构件为机架，则得双摇杆机构。

如果四杆机构不满足杆长和条件，则不论选取哪个构件为机架，所得机构均为双摇杆机构。

需要指出的是：在这种情形下所形成的双摇杆机构与上述双摇杆机构不同，它不存在整转副。