数控r圆弧算法和编程

数控编程圆弧计算方法(一)数控编程圆弧计算方法在数控机床上，圆弧是常见的加工形式之一。

然而，要正确地编写圆弧的数控程序，需要掌握圆弧的计算方法，包括圆弧的起点、终点、半径等参数的计算。

下面将详细介绍数控编程中的圆弧计算方法。

圆弧的定义圆弧是一个弧线形状，由圆锥曲线或球面曲线的一部分组成。

圆弧有起点、终点、圆心和半径等参数。

圆弧的表示方法在数控编程时，圆弧可以用多种方式来表示。

其中一种常用的方式是用圆心坐标及起点、终点的位置坐标来表示。

假设圆弧的起点为P1，终点为P2，圆心为C，半径为R，则圆心坐标可以用以下公式计算：C=(P1+P2)/2+(P1−P2)⊥∗R/(2∗|P1−P2|)其中“+”表示向量加法，“⊥”表示向量垂直，“|.|”表示向量的模。

通过圆心坐标及起点、终点的位置坐标，可以计算出圆弧的圆心角度数、圆弧的弧长等参数。

圆弧的程序调用格式在数控编程中，圆弧通常使用G02或G03指令来表示。

以G02指令为例，其格式为：G02 X_ Y_ I_ J_ R_其中X、Y表示终点坐标，I、J表示圆心坐标与起点的相对距离，R表示圆弧半径。

需要注意的是，只有当起点与当前点之间没有直线段时才能使用I、J参数。

圆弧的误差分析在数控加工中，为了保证加工精度，需要对圆弧误差进行分析。

圆弧误差包括位置误差和形状误差。

位置误差是由起点到圆心、圆心到终点的直线段引起的误差，可以通过适当调整I、J参数来补偿。

形状误差是由数控机床控制系统、加工刀具等因素引起的误差，可以通过加工补偿、精度提高等措施来减小。

总结圆弧计算方法是数控编程中的核心内容之一，正确地编写圆弧程序可以提高加工效率、保证加工精度。

需要掌握圆弧的定义、表示方法、程序调用格式以及误差分析等方面的知识，才能编写出高质量的数控程序。

圆弧计算方法示例以下是一组示例，展示如何通过已知起点、终点和圆弧半径来计算圆心坐标和其他相关参数。

假设起点坐标为(0, 0)，终点坐标为(2, 2)，圆弧半径为1，则可按如下方法计算圆心坐标：C=(P1+P2)/2+(P1−P2)⊥∗R/(2∗|P1−P2|)=(0+2)/2+(0−2,0−2)⊥∗1/(2∗√2)=(1,1)由此可得圆心坐标为(1, 1)。

数控原理圆弧偏差计算公式在数控加工中，圆弧偏差是一个非常重要的概念。

它表示了数控加工中圆弧轮廓与理想圆弧轮廓之间的偏差大小。

圆弧偏差的计算公式可以帮助我们准确地评估加工精度，从而指导加工过程中的调整和改进。

本文将介绍数控原理圆弧偏差的计算公式，并探讨其在数控加工中的应用。

圆弧偏差的计算公式可以分为两种情况，内偏差和外偏差。

内偏差是指实际加工的圆弧轮廓位于理想圆弧轮廓内部的情况，而外偏差则是指实际加工的圆弧轮廓位于理想圆弧轮廓外部的情况。

下面分别介绍这两种情况的计算公式。

首先是内偏差的计算公式。

假设我们要计算一个实际加工的圆弧轮廓与其理想圆弧轮廓之间的内偏差，可以使用以下公式：δi = R (R e) cos(α)。

其中，δi表示内偏差的大小，R表示理想圆弧的半径，e表示实际加工的圆弧轮廓与理想圆弧轮廓之间的偏差，α表示圆弧的角度。

接下来是外偏差的计算公式。

如果我们要计算一个实际加工的圆弧轮廓与其理想圆弧轮廓之间的外偏差，可以使用以下公式：δo = (R + e) cos(α) R。

其中，δo表示外偏差的大小，R表示理想圆弧的半径，e表示实际加工的圆弧轮廓与理想圆弧轮廓之间的偏差，α表示圆弧的角度。

这两个公式可以帮助我们准确地计算出实际加工的圆弧轮廓与其理想圆弧轮廓之间的偏差大小。

通过比较偏差大小与加工精度要求，我们可以对加工过程进行调整和改进，以提高加工精度。

在实际应用中，我们还可以通过数控系统的数据采集功能，实时监测加工过程中圆弧偏差的大小。

通过实时监测，我们可以及时发现加工过程中的问题，并采取相应的措施进行调整，以确保加工精度达到要求。

除了计算偏差大小，我们还可以通过数控系统的仿真功能，对加工过程中的圆弧偏差进行预测和分析。

通过仿真分析，我们可以发现加工过程中可能出现的偏差情况，并提前采取措施进行调整，以避免偏差的发生。

总之，圆弧偏差的计算公式是数控加工中一个非常重要的工具。

它可以帮助我们准确地评估加工精度，指导加工过程中的调整和改进。

第３期（总第１７２期）２０１２年６月机械工程与自动化ＭＥＣＨＡＮＩＣＡＬ　ＥＮＧＩＮＥＥＲＩＮＧ　＆　ＡＵＴＯＭＡＴＩＯＮＮｏ．３Ｊｕｎ．文章编号：１６７２－６４１３（２０１２）０３－００６８－０３数控车床上圆弧螺纹的宏程序编程与加工夏静文１，穆丽沙２（１．山西煤炭职业技术学院，山西　太原　０３００３１；２．山西省应用技术学校，山西　太原　０３００２４）摘要：主要讨论了在数控车床上对圆弧螺纹的加工。

利用ＦＡＮＵＣ　０ｉ—ＴＣ系统数控车床提供的宏功能为各种直径和螺距的圆弧螺纹加工编制了通用的数控车削程序，并详细说明了圆弧螺纹刀具选择和宏程序的参数设置方法。

在程序中巧妙地结合了普通车床车削梯形螺纹时应用的各种工艺技巧，提供了一种有较高实用价值的加工程序。

关键词：圆弧螺纹；宏程序；数控车床加工中图分类号：ＴＧ６５９∶ＴＰ３１１．１ 文献标识码：Ａ收稿日期：２０１２－０１－１６；修回日期：２０１２－０２－１５作者简介：夏静文（１９８２－），男，山西太原人，助教，硕士，研究方向：机械设计与制造。

０　引言数控系统中常用的螺纹切削指令主要是指编制内外圆柱螺纹、内外圆锥螺纹、多线螺纹等较规则和螺距较小的常用联接螺纹的加工程序，且螺纹的牙型也仅限于三角形，多采用直进式进刀方式。

圆弧螺纹深度较深、宽度大、螺距大，采用数控系统自带的标准螺纹切削指令，编制加工半圆形螺纹或圆弧圆心角大于１８０°的圆弧螺纹时，程序编写较复杂繁琐，而且当圆弧型螺纹的导程、公称直径、长度、螺纹槽深、牙宽、圆弧半径等参数中任何一值不同时，就需要重新编制程序。

如果能编写出圆弧形螺纹加工的通用宏程序模板就可以解决这一问题，且可以简化程序，提高生产效率，降低加工成本。

１　圆弧螺纹的加工工艺分析１．１　刀具选择加工圆弧形螺纹时，使用标准数控机夹螺纹车刀是根本不可行的，尖形车刀和宽度较小的普通切槽刀尚可勉强使用标准数控机夹，但若遇到螺纹的弧形大于或等于半圆时，使用尖形车刀和普通切槽刀就会发生干涉。

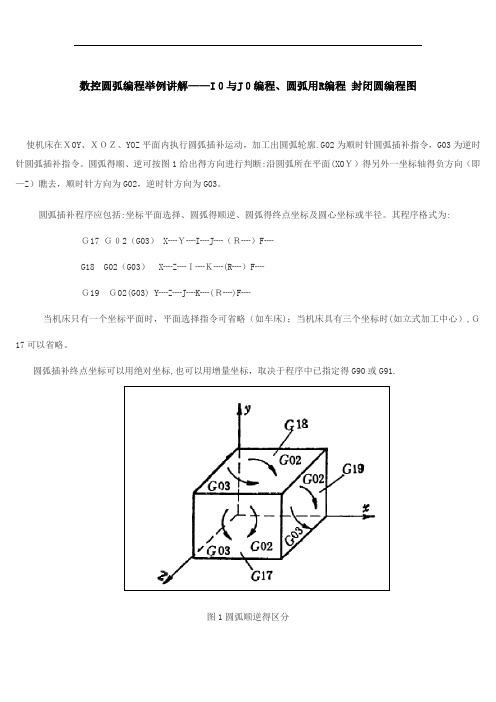
数控圆弧编程举例讲解——I０与J０编程、圆弧用R编程封闭圆编程图使机床在ＸOY、ＸＯＺ、YOZ平面内执行圆弧插补运动，加工出圆弧轮廓.G02为顺时针圆弧插补指令，G03为逆时针圆弧插补指令。

圆弧得顺、逆可按图1给出得方向进行判断:沿圆弧所在平面(XOＹ）得另外一坐标轴得负方向（即—Z）瞧去，顺时针方向为G02，逆时针方向为G03。

圆弧插补程序应包括:坐标平面选择、圆弧得顺逆、圆弧得终点坐标及圆心坐标或半径。

其程序格式为:Ｇ17 Ｇ０2（G03） X┈Ｙ┈I┈J┈（Ｒ┈）F┈G18 G02（G03）X┈Z┈Ｉ┈Ｋ┈(R┈）F┈Ｇ19 Ｇ02(G03) Y┈Z┈J┈K┈(Ｒ┈)F┈当机床只有一个坐标平面时，平面选择指令可省略（如车床)；当机床具有三个坐标时(如立式加工中心）,Ｇ17可以省略。

圆弧插补终点坐标可以用绝对坐标,也可以用增量坐标，取决于程序中已指定得G90或G91.图1圆弧顺逆得区分圆心坐标Ｉ、J、K一般用圆心相对于圆弧起点（矢量方向指向圆心)在X、Y、Z坐标得分矢量，且总就是为增量值（圆弧起点作为圆心坐标得原点），与程序中已指定得G９0无关。

圆心参数也可用半径R。

由于在同一半径R得情况下,从圆弧得起点到终点有两个圆弧得可能性,为区别二者,当圆心角θ≤１80°得圆弧用Ｒ,当θ〉180°得圆弧用-R.用R参数时,不能描述整圆。

应注意得就是,圆弧就是由数控装置得圆弧插补器完成得，若给出得圆弧参数有误差时,圆弧得终点处必残留一个小得直线段而形成圆弧误差ε,一般限制在ε≤10μ。

现代得数控机床都可跨象限编制圆弧程序。

但有些旧式数控机床就是按象限划分程序段得。

图2为封闭圆，用圆心坐标I、J编程。

设刀具起点在坐标原点Ｏ,刀具回转中心快速移到A ,按箭头方向以Ｆ=1０0mm／ｍin速度切削整圆至A,再返回原点。

(1)假定不能跨象限编程，只能按Ⅰ、Ⅱ、Ⅲ、Ⅳ象限分别编程。

用绝对坐标:N0０1 G92 XＯYO ＬFN0０２ G90 G00 X２0 ＹO S200 Ｍ0３ T0１ＬFN003 G０3 X0 Y２0 I—20 J0 Ｆ100 LFＮ00４ X-20 Ｙ０ I0 J-20 LFＮ0０5 X0 Y-20 I2０Ｊ0 LＦN00６Ｘ20 Y0 I０Ｊ20 LFＮ0０7 GOO Ｘ0 Y0 Ｍ0２LF注:Ｉ0与J0可以省略用增量坐标:Ｎ０0１ G91 G０0 X2０ Y0 Ｓ200 M０3 Ｔ0１ LFN０02 Ｇ03 X－20 Y20 I－２0 J０Ｆ10０ＬFN００3 X—2０Y-20 I0 J-20 LＦN０04 X２0 Y—20 I20 J０ LＦN0０５X2０ Y20 I0 J20 LFN00６ＧOＯＸ—20 Ｙ０M02 ＬＦ增量坐标还可以表达为:N00１ G0０ U2０ V0 S2０0 M03 T0１ＬFN002 G03 U—２０Ｖ20 I—20 J0 F100 LFN０0３U—20 V—20 Ｉ0 J-20 LＦN00４ U2０ V-２0 I20 Ｊ０ LFN00５Ｕ20 Ｖ20 Ｉ0 J２0 LFN006 G０0 U-20 V０ M02 ＬF图２封闭圆编程＜＝””>图图３圆弧用R编程(2)可以跨象限编程用绝对坐标:Ｎ00１ G９２ X０ Y0 ＬFN０02 Ｇ90 G00 X20 Ｙ0 Ｓ200 Ｍ03 T01 LFN003 G03 X2０ Y0 Ｉ－20 J０F1０0 LFN００４Ｇ００ X0 Y0 M0２ＬＦ用增量坐标：N０01 G91 G00 X２0 Y0 S200 M03 Ｔ0１ LFN００2 G０３ X0 Ｙ0 I-2０Ｊ0 Ｆ100N003 G０0 X—20 Y0 M0２ LF图3为圆弧插补圆参数用R编程。

数控编程圆弧计算方法在数控加工中，圆弧是一种常见的加工形式。

为实现圆弧加工，在数控编程中需要计算出圆弧的各种参数。

下面介绍数控编程中圆弧计算的方法。

首先需要明确的是，圆弧主要由起点、终点和圆心三个参数来确定。

在数控编程中，通常采用以下两种方法计算圆弧参数：1. 利用坐标计算圆弧参数在此方法中，圆弧的起点和终点坐标已知，需要通过计算圆心坐标来确定圆弧的参数。

具体操作步骤如下：1) 计算圆心坐标圆心坐标可以通过起点和终点坐标以及圆弧半径来计算。

假设起点坐标为(x1,y1)，终点坐标为(x2,y2)，圆弧半径为R，则圆心坐标可表示为：xc = (x1+x2)/2 + (y2-y1)/(2R)yc = (y1+y2)/2 + (x1-x2)/(2R)2) 计算圆弧角度圆弧角度可以通过起点、终点和圆心坐标来计算。

假设圆心坐标为(xc,yc)，起点坐标为(x1,y1)，终点坐标为(x2,y2)，则圆弧角度可表示为：θ = atan2(y2-yc,x2-xc) - atan2(y1-yc,x1-xc)其中，atan2函数是求反正切的函数，它可以将坐标点(x,y)转化为极坐标系下的角度。

3) 计算圆弧方向根据圆弧的起点和终点坐标，可以判断出圆弧的方向是顺时针还是逆时针。

2. 利用半径计算圆弧参数在此方法中，圆弧的起点和终点坐标已知，需要通过计算圆弧半径来确定圆弧的参数。

具体操作步骤如下：1) 计算圆弧中心坐标圆弧中心坐标可以通过起点、终点和圆弧半径来计算。

假设起点坐标为(x1,y1)，终点坐标为(x2,y2)，圆弧半径为R，则圆心坐标可表示为：xc = (x1+x2)/2 + sqrt(R^2 - ((x2-x1)/2)^2)yc = (y1+y2)/2 + sqrt(R^2 - ((y2-y1)/2)^2)2) 计算圆弧角度和方向圆弧角度和方向可以根据起点、终点和圆心坐标来计算，计算方法与上述方法相同。

总之，在数控编程中，圆弧计算是一项非常重要的工作，正确的计算方法可以确保圆弧加工的准确性和效率。

端面圆弧计算公式数控编程数控编程是一种通过计算机控制机床进行加工的技术，它可以大大提高加工效率和精度。

在数控编程中，端面圆弧的计算是非常重要的一部分，因为端面圆弧的加工需要精确的编程来实现。

本文将介绍端面圆弧计算公式在数控编程中的应用。

首先，我们来看一下端面圆弧的定义。

端面圆弧是指在零件的端面上进行的圆弧加工，它通常用于连接两个不同方向的加工面，或者用于修整零件的边缘。

在数控编程中，我们需要计算端面圆弧的起点、终点、半径和角度，然后将这些参数转化为机床可以识别的指令，以实现端面圆弧的加工。

端面圆弧的计算公式如下：1. 端面圆弧的起点坐标计算公式：X1 = X0 + R cos(α)。

Y1 = Y0 + R sin(α)。

其中，(X0, Y0)为圆弧的圆心坐标，R为圆弧的半径，α为圆弧的起始角度。

2. 端面圆弧的终点坐标计算公式：X2 = X0 + R cos(β)。

Y2 = Y0 + R sin(β)。

其中，β为圆弧的终止角度。

3. 端面圆弧的角度计算公式：θ = βα。

4. 端面圆弧的切线方向计算公式：tan(φ) = (Y2 Y1) / (X2 X1)。

以上公式中，X1、Y1为圆弧的起点坐标，X2、Y2为圆弧的终点坐标，θ为圆弧的角度，φ为圆弧的切线方向。

在数控编程中，我们可以根据以上公式计算出端面圆弧的各项参数，然后将这些参数转化为机床可以识别的指令。

例如，对于常见的G代码编程，我们可以使用G02和G03指令来实现端面圆弧的加工。

其中，G02表示顺时针圆弧插补，G03表示逆时针圆弧插补。

通过合理的编程，我们可以实现各种复杂的端面圆弧加工，从而提高加工效率和精度。

除了上述的基本计算公式外，还有一些特殊情况需要考虑。

例如，当圆弧的起点和终点在同一直线上时，需要特殊处理以避免出现意外的加工结果。

此外，当圆弧的半径非常小或非常大时，也需要考虑机床的加工能力和精度，以避免出现加工误差。

总之，端面圆弧的计算公式在数控编程中起着非常重要的作用。

不少人觉得数控车床手工编程遇到圆弧，倒角，计算点位坐标的时候比较繁琐。

今天这篇文章分享两个知识点,让你编程省心又省力。

1, 倒角的图纸标注2，直接图纸编程方法一，倒角的图纸标注1，相互倾斜的两个面上进行倒角，尤其是倒圆角时候，这部分尺寸非常混乱，因此为了明确这部分的尺寸标注，一般情况下，图纸是从倒角的交点处标注。

比如上面简图，两边倒圆角，是以两边延长线的交点P为基准标注的。

而编程的时候，如使用G02/G03需要计算出圆弧起点和终点坐标值。

但是图纸标注的时候大多是以倒角的交点处标注，这也是为什么数车师傅遇到圆弧，采用手工算点比较繁琐的原因了。

2，45度倒角标注，一般用字母C 表示（英语chamfer的第一个字母表示），比如下图：C3此含义是：倒角的斜度为45度，长度为3mm,需要注意的是这个长度不是斜边长度,，而是直边长，如下图所示：二，直接图纸编程方法。

顾名思义也就是按照图纸标注的尺寸来编程。

其格式如下：G01X _Z_R_ (圆弧)G01X _Z_A_ (倒角)也就是在G01指令后面直接添加A或R 。

其中:A为倒角R为倒圆角比如下面简图：A后面的倒角度数是倒角边与Z轴的夹角。

注意：倒角边和Z轴会出现两个比如下面简图：倒角边与Z轴的夹角，仔细看上图，夹角会出现两个数值。

比如C3的倒角：(夹角开口朝向)与Z轴正方向夹角135°与Z轴负方向夹角45°比如上图20度的倒角：与Z轴正方向夹角160°与Z轴负方向夹角20°好，我上面编程的时候选择了与Z轴负方向的夹角，所以A后面为负。

当然你也可以选择与Z轴正方向的夹角，那么下面程序完全等同于上面程序：基于以上分析，我们看下面简图的程序：（车内孔）备注：在用直接图纸编程方式的时候，有些机床需要在A，或R前面添加“逗号”。

比如：G01X24. ,A45.G01 X30. ,A20. ,R5.你可以找到系统参数#3405把第四位CCR设为1，那么字母A，R前面就不需要添加“逗号”。

数控编程圆弧计算方法
数控编程是机械加工中非常重要的一部分，它可以通过编程来控制机床进行加工。

其中圆弧计算是数控编程中的一个重要内容，因为很多零件都包含有圆弧形状，准确计算圆弧可以保证零件的精度和质量。

数控编程圆弧计算方法主要包括以下几个方面：
1. 圆弧的半径计算：在圆弧加工中，半径是一个非常重要的参数，需要根据零件图纸中给出的半径进行计算。

计算方法是：半径=圆弧的直径÷2。

2. 圆弧的圆心计算：圆弧的圆心是计算圆弧路径的重要参数，需要根据零件图纸中给出的圆心坐标进行计算。

计算方法是：圆心坐标=起点坐标+向量1+向量2，其中向量1和向量2可以根据起点、终点和半径计算得出。

3. 圆弧的切线方向计算：圆弧的切线方向是计算进给速度和刀具路径的重要参数，需要根据圆心坐标和半径计算得出。

计算方法是：切线方向=圆心坐标-起点坐标或终点坐标-圆心坐标，这两个向量都是在圆弧平面内的向量。

4. 圆弧的角度计算：圆弧的角度是计算圆弧路径长度和编程精度的重要参数，需要根据圆弧的半径和圆心角度计算。

计算方法是：角度=圆心角度×π÷180，其中π是圆周率，180是角度制和弧度制之间的转换因子。

数控编程圆弧计算方法是数控编程中的基础知识之一，掌握了这些计算方法可以提高圆弧加工的精度和效率。

同时，在数控编程中，还有很多其他的计算方法和技巧需要掌握，只有不断学习和实践才能成为一名优秀的数控编程工程师。

规定圆心角≤180°时，由于在同一半径只的情况下，圆弧终点坐标为圆弧终点在工件坐标系中的坐标值，从圆弧的起点到终点有两个圆弧的可能性，用U。

本系统I、用半径只指定圆心位置时，并带有“±”号、K为增量值。

2、半径、K为圆弧起点到圆弧中心所作矢量分别在X，当分矢量的方向与坐标轴的方向不一致时取“－”号。

若圆弧圆心角gt、圆心坐标I，用“＋R”表示、W表示G2或G3 X Z 的终点坐标CR= （R多少）3，不能描述整圆，要么是简单的加减法，需要在图纸上标出来N1 G92 X40 Z5 （设立坐标系，定义对刀点的位置）N2 M03 S400 （主轴以400r min旋转）N3 G00 X0 （到达工件中心）N4 G01 Z0 F60 （工进接触工件毛坯）N5 G03 U24 W-24 R15 （加工R15圆弧段）N6 G02 X26 Z-31 R5 （加工R5圆弧段）N7 G01 Z-40 （加工Φ26外圆）N8 X40 Z5 （回对刀点）N9 M30 （主轴停、主程序结束并复位）数控车床与普通车床相比具有适应性强，加工精度高，生产效率高，能完成复杂型面的加工等特点。

随着新产品的开发，其形状越来越复杂，精度要求也越来越高，无疑要充分发挥数控车床的优点。

圆弧加工就体现了数控车床的优点。

但是，在实际加工大圆弧时，由于加工工艺的选择不当或缺少辅助计算工具常常出现编程困难，重者出现异常加工误差。

对此引起了我的注意，通过长期的试切实验，证明应用下面方法在圆弧编程中思路简单，加工出的零件精度高。

下面我以几种常见零件为例与大家一起讨论。

一、圆弧分层切削法1. 圆弧始点、终点均不变，只改变半径R在零件加工一个凸圆弧，根据过两点作圆弧，半径越小曲率越大的原则，因此在切削凸圆弧时，可以固定始点和终点把半径R由小逐渐变大至规定尺寸。

但要注意，圆弧半径最小不得小于成品圆弧弦长的一半。

N10 G01 X40 Z-5 F0.3; N20 G03 X40 Z-25 R10.2 F0.2; N30 G00 X53; N40 Z-5;N50 G01 X40 F0.3;N60 G03 X40 Z-25 R12 F0.2; N70 G00 X53; N80 Z-5;N90 G01 X40 F0.3;N100 G03 X40 Z-25 R16 F0.1 :2. 圆弧始点、终点坐标变化，半径R不变在零件上加工一个凹圆弧，为了合理分配吃刀量，保证加工质量，采用等半径圆弧递进切削，编程思路简单。