画三视图专项练习

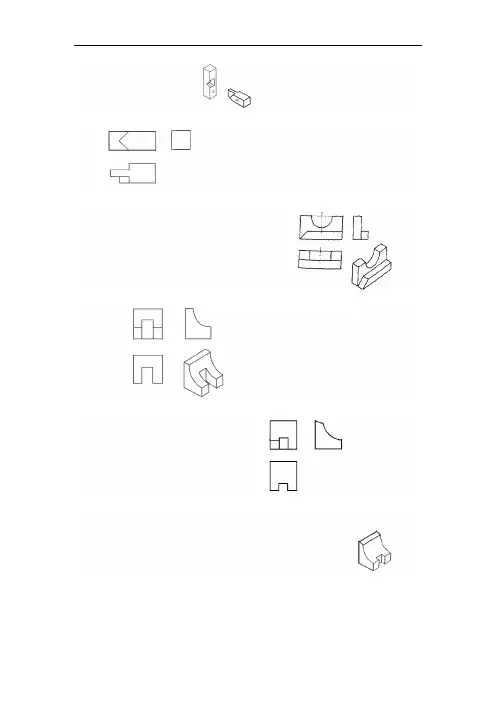
三视图绘制班级姓名1．由视图画三视图２．由视图画三视图３．由视图画三视图４．由视图画三视图三视图绘班姓５．由视图画三视６．由视图画三视７．由视图画三视图８．由视图画三视图主视图方向三视图绘制班级姓名1．由视图画三视图２．由视图画三视图３．由视图画三视图４．由视图画三视图三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条８．添加所缺的三条三视图绘制班级姓名1．添加所缺的三条线2．添加所缺的三条线3．添加所缺的三条线4．添加所缺的三条线．添加所缺的三条．添加所缺的三条7．添加所缺的三条线8．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线三视图绘制班级姓名1．添加所缺的三条线２．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘班姓５．添加所缺的三条６．添加所缺的三条７．添加所缺的三条线８．添加所缺的三条线。

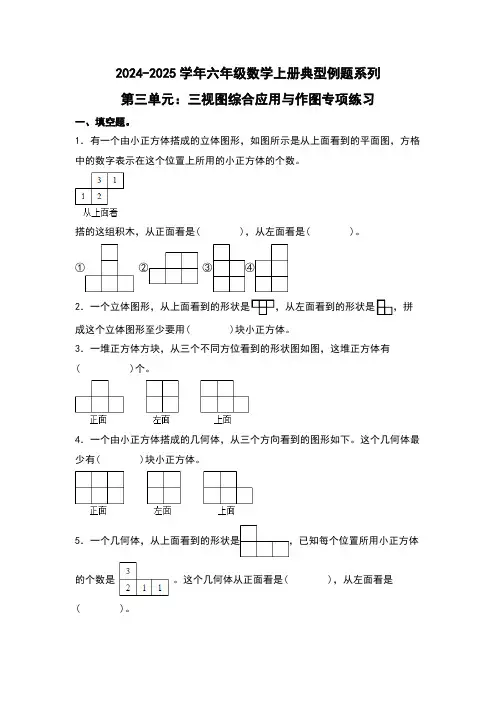
2024-2025学年六年级数学上册典型例题系列第三单元：三视图综合应用与作图专项练习一、填空题。

1．有一个由小正方体搭成的立体图形，如图所示是从上面看到的平面图，方格中的数字表示在这个位置上所用的小正方体的个数。

搭的这组积木，从正面看是( )，从左面看是( )。

①②③④2．一个立体图形，从上面看到的形状是，从左面看到的形状是，拼成这个立体图形至少要用( )块小正方体。

3．一堆正方体方块，从三个不同方位看到的形状图如图，这堆正方体有( )个。

4．一个由小正方体搭成的几何体，从三个方向看到的图形如下。

这个几何体最少有( )块小正方体。

5．一个几何体，从上面看到的形状是，已知每个位置所用小正方体的个数是。

这个几何体从正面看是( )，从左面看是( )。

6．一个由若干个相同小正方体摆成的立体图形，从上面看到的形状如下图，上面的数字表示这个位置所用的小正方体个数。

摆这个立体图形一共用了( )个小正方体，从左面看到的形状是图( )（填甲或乙）。

7．如果要搭建一个从正面、左面、上面看到的图形都是的几何体，至少需要( )个。

8．一个立体图形，从上面看是，从左面看是，要搭成这样的立体图形，至少要用( )个小正方体。

9．用小正方体搭成的立体图形，从左面看，从正面看，搭这个立体图形最少用( )个小正方体。

10．用小正方体摆一个几何体，从上面看是的，从左面看是的，摆这个几何体最少用( )个小正方体，最多用( )个小正方体。

11．小明用小正方体积木搭成的图形，从上面看是这样的积木上面的数字表示这个位上所用小正方体的个数。

那么，这个搭成的图形从正面看是( )，从左面看是( )。

①②③④12．一个几何体，从上面看到的图形是，从正面看到的图形是，搭这样一个几何体，最少需要( )个小正方体。

13．用小正方体搭建几何体，从三个方向看到的图形如下，搭建这个几何体一共要( )个小正方体。

从上面看：从正面看：从左面看：14．小芳用几个同样的小正方体摆几何体，从上面和正面看到的形状都是。

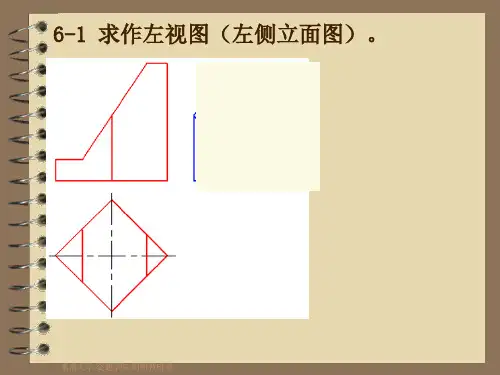
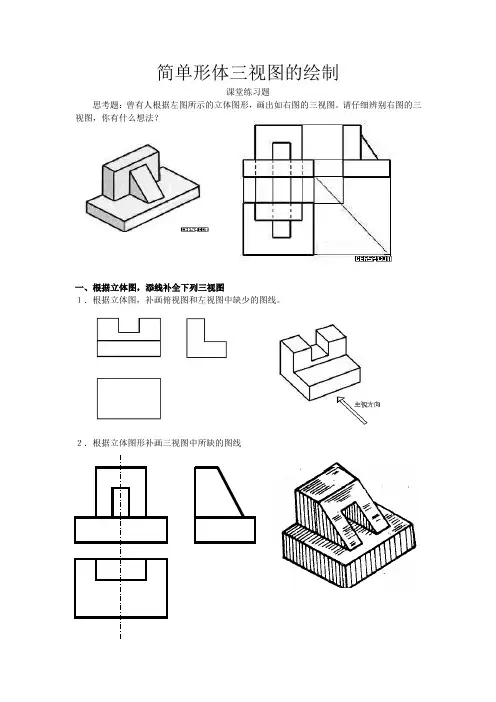
简单形体三视图的绘制
课堂练习题
思考题：曾有人根据左图所示的立体图形，画出如右图的三视图。

请仔细辨别右图的三视图，你有什么想法？
一、根据立体图，添线补全下列三视图
１．根据立体图，补画俯视图和左视图中缺少的图线。

２．根据立体图形补画三视图中所缺的图线
３．根据题图所示形体，（1）画出主视图。

（2）补全左视图的缺漏线条。

４．根据题图所示形体，（1）画出主视图。

（2）补全俯视图的缺漏线条。

二、作出下列模型的三视图
三、形体尺寸的标注
根据所给视图和立体图，补齐三视图中的缺线，并在三视图中标注该组合体的总长、总宽、总高。

尺寸从图中量取，以mm为单位取整数。

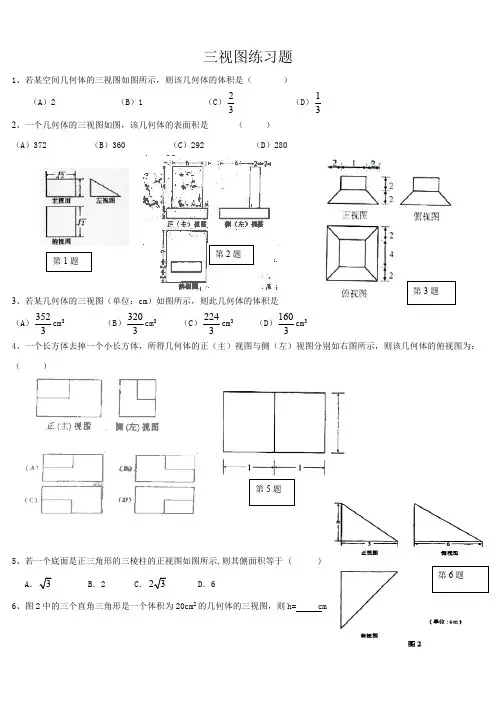
三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为 。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为 （）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

2023-2024学年四年级数学下册第二单元：三视图的判断、确认与绘制专项练习一、填空题。

1．看一看，填一填。

(1)从左面看是图形A的有( )。

(2)从正面看是图形A的有( )。

【答案】(1)①②④(2)①【分析】先观察题中四个几何体，再分别从正面、侧面观察这些物体，然后把观察到的形状分别与图形A对照做出选择。

【详解】（1）从左面看是图形A的有①②④。

（2）从正面看是图形A的有①。

【点睛】本题是考查从不同方向观察物体和几何图形，要求学生发挥观察能力和想象能力，能正确看出从正面、侧面、上面观察看到的平面图形，体验从不同的位置观察立体图形所看到的形状可能不同，关键是培养学生的观察能力。

2．哪个几何体符合从正面看是，从上面看是的要求？在括号里打“√”。

【答案】见详解【分析】第一个图形从正面看到的图形是，从上面看到的图形是；第二个图形从正面看到的图形是，从上面看到的图形是；第三个图形从正面看到的图形是，从上面看到的图形是。

【详解】如图所示：【点睛】本题考查观察物体，明确从正面和上面看到的形状是解题的关键。

3．从不同方向看图1，则图2是从( )面看到的，图3是从( )面看到的。

【答案】上左【分析】从上面看，可以看到左边是一个长方形，中间是一个圆，右边是一个中间有一个点的圆；从左面看，圆挡住了三角形的一部分，长方形挡住了圆的一部分。

据此解答。

【详解】由分析可知：从不同方向看图1，则图2是从上面看到的，图3是从左面看到的。

【点睛】本题考查从不同的方向观察物体。

4．下面分别是从哪个面看到的图形，填在括号里。

( )面 ( )面 ( )面【答案】正右上【分析】观察立体图形可知，这个图形是由5个相同的小正方体组成。

从正面能看到4个小正方形，分两层，下层3个，上层1个且居右；从右面能看到3个小正方形，分两层，下层2个，上层1个且居右；从上面能看到4个小正方形，分两层，上层3个，下层1个且居中。

据此判断三个平面图是从哪个面看到的。

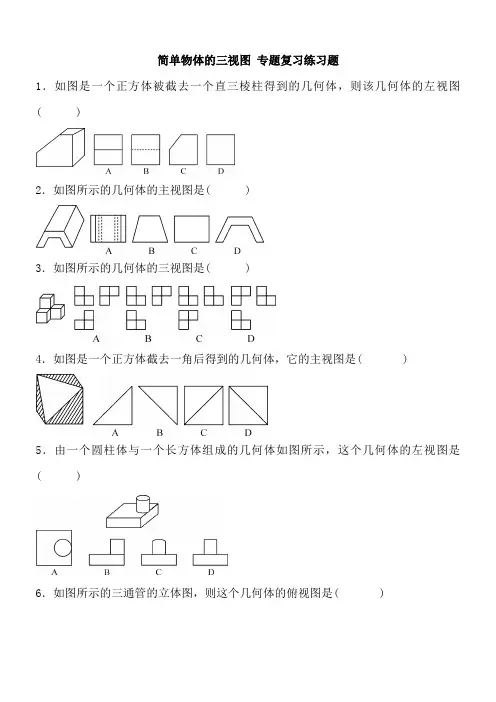
简单物体的三视图专题复习练习题1．如图是一个正方体被截去一个直三棱柱得到的几何体，则该几何体的左视图( )2．如图所示的几何体的主视图是( )3．如图所示的几何体的三视图是( )4．如图是一个正方体截去一角后得到的几何体，它的主视图是( )5．由一个圆柱体与一个长方体组成的几何体如图所示，这个几何体的左视图是( )6．如图所示的三通管的立体图，则这个几何体的俯视图是( )7. 如图所示的零件的左视图是( )8. 如图，从不同方向看一只茶壶，你认为其俯视图可能是( )9. 在生活和生产实践中，我们经常需要运用三视图来描述物体的形状和大小．小亮在观察如图所示的热水瓶时，得到的左视图是( )10. 如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三视图中面积最小的是___________．11. 如图，图①是一个水平摆放的小正方体木块，图②③是由这样的小正方体木块按一定的规律叠放而成．其中图①的主视图有1个正方形，图②的主视图有4个正方形，图③的主视图有9个正方形，按照这样的规律继续叠放下去，则图⑩的主视图有_________个正方形．12. 两个正方体形状的积木摆成如图所示的塔形平放于桌面上，上面正方体下底面的四个顶点恰好是正面相邻正方体的上底面各边的中点，并且下面正方体的棱长为1，则能被看到部分的面积为______．13. 已知某几何体的主视图和俯视图如图所示．(1)画出该几何体的左视图；(2)该几何体是几面体？它有多少条棱？多少个顶点？(3)该几何体的表面有哪些你熟悉的平面图形？14. 如图，一个工件是由大长方体上面中间部位挖去一个小长方体后形成的，主视图是凹字形的轴对称图形．(1)请补画该工件的俯视图；(2)若该工件的前侧面(即主视图部件)需涂油漆，根据图中尺寸(单位：cm)，计算需涂油漆部位的面积．15．墙角处有若干个大小相同的小正方体堆成如图所示的立体图形，如果你打算搬走其中部分小正方体，但希望搬完后该立体图形的主视图、左视图和俯视图都不变，那么你最多可以搬走____个小正方体？16．如图，上、下底面为全等的正六边形礼盒，其主视图与左视图均由矩形构成，主视图中大矩形边长如图所示，左视图中包含两个全等的矩形，如果用彩色胶带按如图所示的方式包扎礼盒，那么所需胶带长度至少为多少厘米？(结果精确到1 cm)答案：1---9 ADCCD ABAB 10. 左视图 11. 100 12. 713. 解：(1)略 (2)六 12 8 (3)梯形，正方形 14. 解：(1)俯视图如图(2)57 cm 215. 解：搬走最多的小正方体方案不唯一，如：第1列最多可以搬走9个小正方体；第2列最多可以搬走8个小正方体；第3列最多可以搬走3个小正方体；第4列最多可以搬走5个小正方体；第5列最多可以搬走2个小正方形．最多可以搬9＋8＋3＋5＋2＝27(个)16. 解：根据题意，作出实际图形的上底面，如解图．AC ，CD 是上底面的两边，过点C 作CB ⊥AD 于点B .易得∠ACD ＝120°，AC ＝CD ，CB ⊥AD ，∴∠CDB ＝30°，∴CB ＝12CD .∵最长对角线长60 cm ，∴2CB ＋CD ＝60 cm ，∴CB ＝15 cm ，CD ＝30 cm ，∴BD ＝153，∴AD ＝30 3 cm.∴胶带的长至少为303×6＋20×6≈432(cm)。

画三视图练习题1．下面是一些立体图形的三视图，?请在括号内填上立体图形的名称．2．如图4-3-26，下列图形都是几何体的平面展开图，你能说出这些几何体的名称吗？3．如图，从不同方向看下面左图中的物体，右图中三个平面图形分别是从哪个方向看到的？4．一天，小明的爸爸送给小明一个礼物，小明打开包装后画出它的主视图和俯视图如图所示．根据小明画的视图，你猜小明的爸爸送给小明的礼物是A．钢笔 B．生日蛋糕 C．光盘 D．一套衣服5．一个几何体的主视图和左视图如图所示，它是什么几何体？请你补画出这个几何体的俯视图．6．一个物体的三视图如图所示，试举例说明物体的形状．7．已知一个几何体的三视图如图所示，则该几何体的体积为多少？8．已知几何体的主视图和俯视图如图所示．画出该几何体的左视图；该几何体是几面体？它有多少条棱？多少个顶点？该几何体的表面有哪些你熟悉的平面图形？9．小刚的桌上放着两个物品，它的三视图如图所示，你知道这两个物品是什么吗？10．一个由几个相同的小立方体搭成的几何体的俯视图如图所示，方格里的数字表示该位置的小立方体的个数，请你画出这个几何体的主视图和左视图．11．如图所示，下列三视图所表示的几何体存在吗？如果存在，请你说出相应的几何体的名称．12．由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示，俯视图的方格中的字母和数字表示该位置上小立方体的个数，求x，y的值．13．马小虎准备制作一个封闭的正方体盒子，他先用5?个大小一样的正方形制成如图所示的拼接图形，经折叠后发现还少一个面，请你在下图中的每个图形上再接一个正方形，?使新拼接成的图形经过折叠能成为一个封闭的正方体盒子．14．由几个小立方体叠成的几何体的主视图和左视图如图，求组成几何体的小立方体个数的最大值与最小值．参考答案:1．圆柱，正三棱锥．圆锥圆柱正方体三棱柱3．上正侧．B ．略6．如粉笔，灯罩等．1208．略六面体，12条，8个等腰梯形，?正方形9．长方体木板的正前方放置了一个圆柱体 10．略 11．不存在12．x=1或x=2，y= 13．略 14．12个，7个1.1.5三视图课程学习目标［课程目标］目标重点：正投影与三视图的画法与应用, 目标难点：三视图的画法以及应用学法关键1．画三视图时，可以把垂直投影面的视线想象成平行光线从不同的方向射向几何体，体会可见的轮廓线的投影就是所要画出的视图，画出的三视图要检验是否符合.长对正、高平齐、宽相等.的基本特征.2．由三视图想象几何体时也要根据.长对正、高平齐、宽相等.的基本特征，想象视图中每部分对应的实物的形象，特别注意几何体中与投影面垂直或平行的线及面的位置研习教材重难点研习点1 正投影1．定义：在物体的平行投影中，如果投射线与投射面垂直，则称这样的平行投影为正投影.. 正投影的性质：①直线或线段的平行投影仍是直线或线段；②平行直线的平行投影是平行或重合的直线；③平行于投影面的线段，它的投影与这条线段平行且等长；④与投影面平行的平面图形，它的投影与这个图形全等；⑤在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比；⑥垂直于投影面的直线或线段的正投影是点；⑦垂直于投影面的平面图形的正投影是直线或直线的一部分.研习点三视图1. 水平投射面：一个投射面水平放置，叫做水平投射面.. 俯视图：投射到水平投射面内的图形叫做俯视图.3. 直立投射面：一个投射面放置在正前方，这个投射面叫做直立投射面.. 主视图：投射到直立投射面内的图形叫做主视图.5. 侧立投射面：和直立、水平两个投射面都垂直的投射面叫做侧立投射面.. 左视图：投射到侧立投射面内的图形叫做左视图.7. 三视图：将空间图形向水平投射面、直立投射面、侧立投射面作正投影，然后把这三个投影按一定的布局放在一个平面内，这样构成的图形叫做空间图形的三视图.研习点3．三视图的画法要求:三视图的主视图、俯视图、左视图分别是人从物体的正前方、正上方、正左方看到的物体轮廓线的正投影组成的平面图形；一个物体的三视图的排列规则是：俯视图放在主视图的下面，长度与主视图一样，左视图放在主视图的右面，高度与主视图一样，宽度与俯视图的宽度一样；记忆口诀：长对正，高平齐，宽相等；主左一样高，主俯一样长，俯、左一样宽。

三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为 。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为 （）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

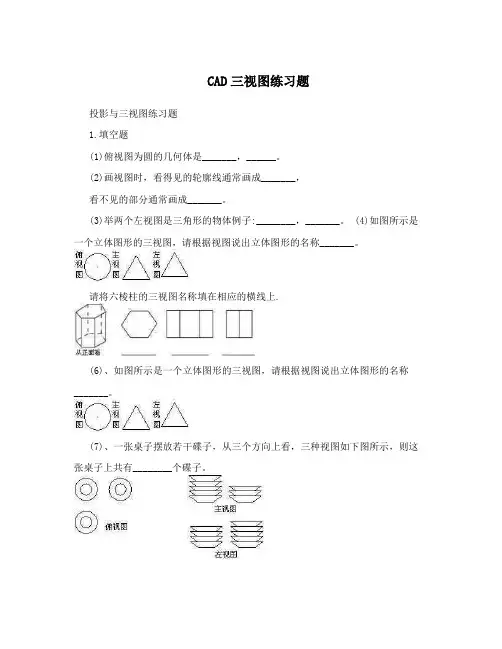
CAD三视图练习题投影与三视图练习题1.填空题(1)俯视图为圆的几何体是_______，______。

(2)画视图时，看得见的轮廓线通常画成_______，看不见的部分通常画成_______。

(3)举两个左视图是三角形的物体例子:________，_______。

(4)如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称_______。

请将六棱柱的三视图名称填在相应的横线上.(6)、如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称_______。

(7)、一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有________个碟子。

(8)、某几何体的三种视图分别如下图所示，那么这个几何体可能是_____。

(9)人在观察目标时，从眼睛到目标的叫做视线。

所在的位置叫做视点，有公共的两条所成的角叫做视角。

视线不能到达的区域叫做。

(10)物体在光线的照射下，在某个内形成的影子叫做，这时光线叫做，投影所在的叫做投影面。

由的投射线所形成的投影叫做平行投影。

由的投射线所形成的投影叫做中心投影。

(11)在平行投影中，如果投射线垂直于投影面，那么这种投影就称为正投影。

(12)物体的三视图是物体在三个不同方向的。

上的正投影就是主视图，水平面上的正投影就是，上的正投影就是左视图。

2.选择题(1)圆柱对应的主视图是( )。

(A) (B) (C) (D)(2)某几何体的三种视图分别如下图所示，那么这个几何体可能是( )。

(A)长方体 (B)圆柱 (C)圆锥 (D)球(3)下面是空心圆柱在指定方向上的视图，正确的是…( )(4)一个四棱柱的俯视图如右图所示，则这个四棱柱的主视图和左视图可能是( )(5)主视图、左视图、俯视图都是圆的几何体是( )。

(A)圆锥(B)圆柱 (C)球 (D)空心圆柱(6)在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下( )A、小明的影子比小强的影子长B、小明的影子比小强的影子短C、小明和小强的影子一样长D、无法判断谁的影子长 3、解答题(1)根据要求画出下列立体图形的视图。