高二数学三视图专项练习
- 格式:doc
- 大小:2.08 MB
- 文档页数:26
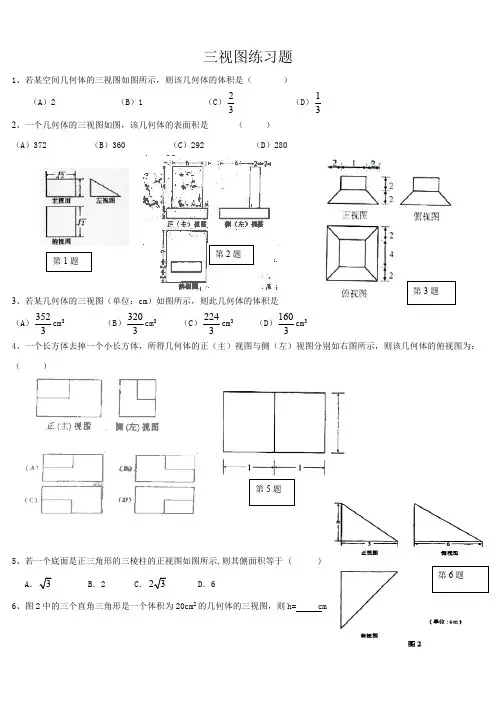
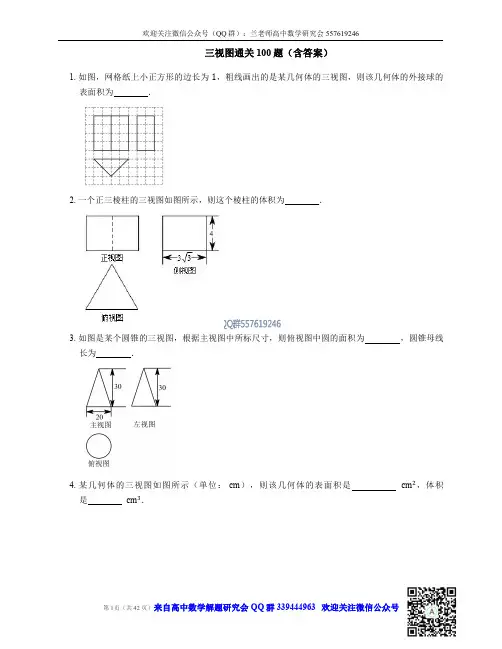
三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是()(A)2(B)1(C)23(D)132、一个几何体的三视图如图,该几何体的表面积是()(A)372 (B)360 (C)292 (D)2803、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是(A)3523cm3(B)3203cm3 (C)2243cm3(D)1603cm34、一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为:()5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB.2 C..66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为 。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图)是( )10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .B .C .D .9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为 ()(A )(B )(C )(D )13、若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 3cm .14、设某几何体的三视图如上图所示。
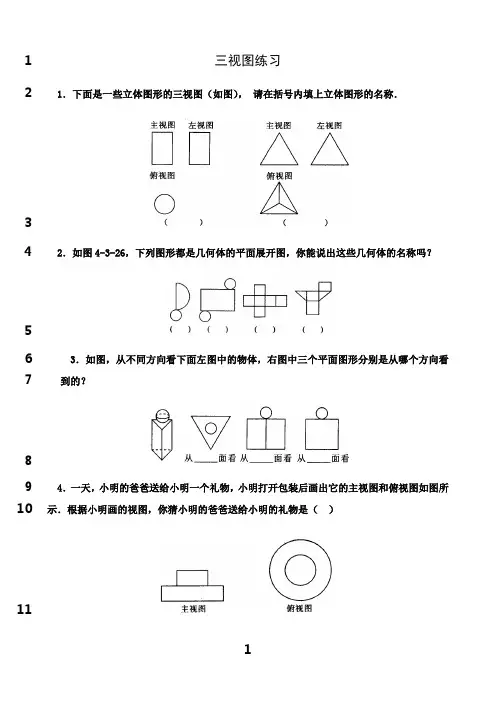
三视图练习121.下面是一些立体图形的三视图(如图),•请在括号内填上立体图形的名称.342.如图4-3-26,下列图形都是几何体的平面展开图,你能说出这些几何体的名称吗?563.如图,从不同方向看下面左图中的物体,右图中三个平面图形分别是从哪个方向看7到的?894.一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的主视图和俯视图如图所10示.根据小明画的视图,你猜小明的爸爸送给小明的礼物是()1112A.钢笔 B.生日蛋糕 C.光盘 D.一套衣服135.一个几何体的主视图和左视图如图所示,它是什么几何体?请你补画出这个几何体14的俯视图.1516176.一个物体的三视图如图所示,试举例说明物体的形状.18197.已知一个几何体的三视图如图所示,则该几何体的体积为多少?20218.已知几何体的主视图和俯视图如图所示.22(1)画出该几何体的左视图;23(2)该几何体是几面体?它有多少条棱?多少个顶点?24(3)该几何体的表面有哪些你熟悉的平面图形?2526279.小刚的桌上放着两个物品,它的三视图如图所示,你知道这两个物品是什么吗?2829303110.一个由几个相同的小立方体搭成的几何体的俯视图如图所示,方格里的数字表示该32位置的小立方体的个数,请你画出这个几何体的主视图和左视图.33343511.如图所示,下列三视图所表示的几何体存在吗?如果存在,请你说出相应的几何体36的名称.3712.由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图38 的方格中的字母和数字表示该位置上小立方体的个数,求x ,y 的值.394041 13.马小虎准备制作一个封闭的正方体盒子,他先用5•个大小一样的正方形制成如图42 所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的每个图形上再43 接一个正方形,•使新拼接成的图形经过折叠能成为一个封闭的正方体盒子.(注:添加44 的正方形用阴影表示)4546 14.由几个小立方体叠成的几何体的主视图和左视图如图,求组成几何体的小立方体47 个数的最大值与最小值.4849 1.如图,在长方体1111ABCD A B C D -中,3cm AB AD ==,12cm AA =, 50 则四棱锥11A BB D D -的体积为 cm 3.51 2.某三棱锥的三视图如图所示,该三梭锥的表面积是( )5253 A. 28+65 B. 30+65 C. 56+ 125 D. 60+12554 555657 5859 60 61 6263 64 65 66 67 6869DABC 1C 1D 1A1B7. 一个多面体的三视图分别为正方形、等腰三角形和矩形,如图所示,则该多面体的体积70为( )71A.24 cm3 B.48 cm3 C.32 cm3D.28 cm37273第7题第8题748.若正四棱锥的正(主)视图和俯视图如图所示,则该几何体的表面积是( ).75A.4 B.4+410 C.8 D.4+41176779.如下图是某几何体的三视图,其中正(主)视图是腰长为2的等腰三角形,侧(左)视图是78半径为1的半圆,则该几何体的体积是( ).79A.π B..π3C.3π D.3π3808182第9题第10题8384 10.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的85 体积是( )86 A.34000cm 3 B.38000cm 3C.32000cmD.34000cm 87 11.如图,一个空间几何体的正视图、侧视图都是面积为3,且一个内角为60的菱形,俯88 视图为正方形,那么这个几何体的表面积为( ) 89 A .23 B .43 C . 4D . 89091 第11题 第12题 第13题 92 12.一空间几何体的三视图如图所示,则该几何体的体积为( ).93 A.223π+ B. 423π+ C. 232π+234π+94 13.如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是( ) 95 A. 2(202)cm + B.21 cm C. 2(242)cm + D. 24 cm 96 14.若一个螺栓的底面是正六边形,它的正(主)视图和俯视图如图所示,则它的体积是97 ( ).9899A.273+12π B.93+12π C.273+3π D.543+3π100101第14题第15题10215.一个五面体的三视图如下,正视图与侧视图是等腰直角三角形,俯视图为直角梯形,部103分边长如图所示,则此五面体的体积为___________.104105第16题第17题10616. 如图是一个几何体的三视图,若它的体积是33a __________10717.设某几何体的三视图如下(尺寸的长度单位为m)。
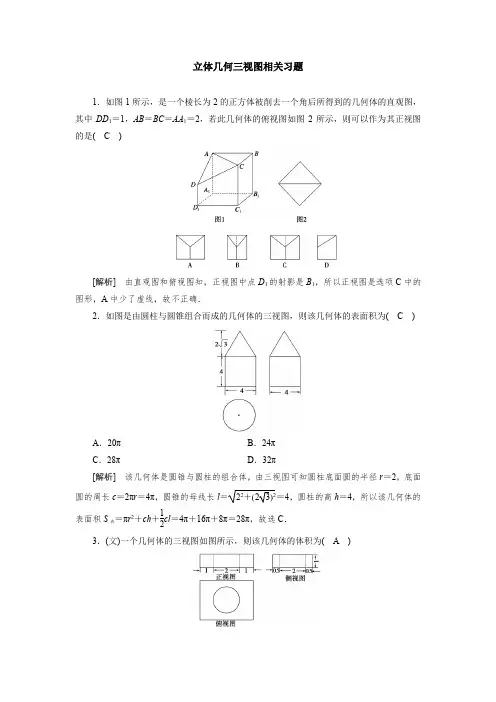
立体几何三视图相关习题1.如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中DD 1=1,AB =BC =AA 1=2,若此几何体的俯视图如图2所示,则可以作为其正视图的是( C )[解析] 由直观图和俯视图知,正视图中点D 1的射影是B 1,所以正视图是选项C 中的图形,A 中少了虚线,故不正确.2.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( C )A .20πB .24πC .28πD .32π[解析] 该几何体是圆锥与圆柱的组合体,由三视图可知圆柱底面圆的半径r =2,底面圆的周长c =2πr =4π,圆锥的母线长l =22+(23)2=4,圆柱的高h =4,所以该几何体的表面积S 表=πr 2+ch +12cl =4π+16π+8π=28π,故选C .3.(文)一个几何体的三视图如图所示,则该几何体的体积为( A )A .12-πB .12-2πC .6-πD .4-π[解析] 由三视图知,该几何体是一个组合体,由一个长方体挖去一个圆柱构成,长方体的长、宽高为4,3,1,圆柱底半径1,高为1,∴体积V =4×3×1-π×12×1=12-π.(理)若某棱锥的三视图(单位:cm)如图所示,则该棱锥的体积等于( B )A .10 cm 3B .20 cm 3C .30 cm 3D .40 cm 3[解析] 由三视图知该几何体是四棱锥,可视作直三棱柱ABC -A 1B 1C 1沿平面AB 1C 1截去一个三棱锥A -A 1B 1C 1余下的部分.∴VA -BCC 1B 1=VABC -A 1B 1C 1-VA -A 1B 1C 1=12×4×3×5-13×(12×4×3)×5=20cm 3.4.某几何体的三视图如图所示,则该几何体的表面积为( B )A .18+2πB .20+πC .20+π2D .16+π[解析] 由三视图可知,这个几何体是一个边长为2的正方体割去了相对边对应的两个半径为1、高为1的14圆柱体,其表面积相当于正方体五个面的面积与两个14圆柱的侧面积的和,即该几何体的表面积S =4×5+2×2π×1×1×14=20+π.故选B .5.(2018·双鸭山一模)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接球的表面积为( A )A .16π3B .8π3C .4 3D .23π[解析] 由已知几何体的正视图是一个正三角形,侧视图和俯视图均为三角形,可得该几何体有一个侧面P AC 垂直于底面,高为3,底面是一个等腰直角三角形的三棱锥,如图.则这个几何体的外接球的球心O 在高线PD 上,且是等边三角形P AC 的中心, 这个几何体的外接球的半径R =23PD =233.则这个几何体的外接球的表面积为S =4πR 2=4π×(233)2=16π3.6.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为16.[解析] 利用三棱锥的体积公式直接求解.VD 1-EDF =VF -DD 1E =13SD 1DE ·AB =13×12×1×1×1=16.7.已知E ,F 分别是矩形ABCD 的边BC 与AD 的中点,且BC =2AB =2,现沿EF 将平面ABEF 折起,使平面ABEF ⊥平面EFDC ,则三棱锥A -FEC 2π. [解析] 如图,平面ABEF ⊥平面EFDC ,AF ⊥EF ,所以AF ⊥平面ECDF ,将三棱锥A -FEC 补成正方体ABC ′D ′-FECD . 依题意,其棱长为1,外接球的半径R =32, 所以外接球的体积V =43πR 3=43π·(32)3=32π.8.(文)如图,三棱柱ABC -A 1B 1C 1中,CA =CB ,AB =AA 1,∠BAA 1=60°.(1)证明:AB ⊥A 1C ;(2)若AB =CB =2,A 1C =6,求三棱柱ABC -A 1B 1C 1的体积. [解析] (1)取AB 的中点O ,连接OC ,OA 1,A 1B . 因为CA =CB ,所以OC ⊥AB .由于AB =AA 1,∠BAA 1=60°,故△AA 1B 为等边三角形,所以OA 1⊥AB . 因为OC ∩OA 1=O ,所以AB ⊥平面OA 1C . 又A 1C ⊂平面OA 1C ,故AB ⊥A 1C .(2)由题设知△ABC 与△AA 1B 都是边长为2的等边三角形,所以OC =OA 1= 3. 又A 1C =6,则A 1C 2=OC 2+OA 21,故OA 1⊥OC .因为OC ∩AB =O ,所以OA 1⊥平面ABC ,OA 1为三棱柱ABC -A 1B 1C 1的高. 又△ABC 的面积S △ABC = 3.故三棱柱ABC -A 1B 1C 1的体积V =S △ABC ×OA 1=3. (理)如图,四棱锥P -ABCD 中,侧面P AD 为等边三角形且垂直于底面ABCD ,AB =BC=12AD ,∠BAD =∠ABC =90°. (1)证明:直线BC ∥平面P AD ;(2)若△PCD 的面积为27,求四棱锥P -ABCD 的体积. [解析] (1)证明:在平面ABCD 内,因为∠BAD =∠ABC =90°,所以BC ∥AD .又BC ⊄平面P AD ,AD ⊂平面P AD , 故BC ∥平面P AD .(2)如图,取AD 的中点M ,连接PM ,CM .由AB =BC =12AD 及BC ∥AD ,∠ABC =90°得四边形ABCM 为正方形,则CM ⊥AD .因为侧面P AD 为等边三角形且垂直于底面ABCD , 平面P AD ∩平面ABCD =AD , 所以PM ⊥AD ,PM ⊥底面ABCD . 因为CM ⊂底面ABCD , 所以PM ⊥CM .设BC =x ,则CM =x ,CD =2x ,PM =3x ,PC =PD =2x . 如图,取CD 的中点N ,连接PN ,则PN ⊥CD , 所以PN =142x . 因为△PCD 的面积为27, 所以12×2x ×142x =27,解得x =-2(舍去)或x =2.于是AB =BC =2,AD =4,PM =2 3.所以四棱锥P -ABCD 的体积V =13×2(2+4)2×23=4 3.。
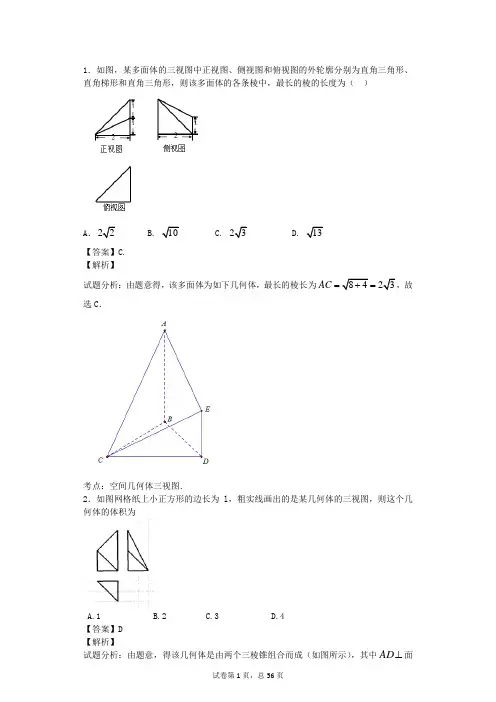
1.如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形,则该多面体的各条棱中,最长的棱的长度为()A.22 B. 10 C. 23 D. 13【答案】C.【解析】AC=+=,故试题分析:由题意得,该多面体为如下几何体,最长的棱长为8423选C.考点:空间几何体三视图.2.如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为A.1B.2C.3D.4【答案】D【解析】AD面试题分析:由题意,得该几何体是由两个三棱锥组合而成(如图所示),其中⊥ABC ,⊥CE 面ABC , BCAC ⊥,4,2====CE AD BC AC ,则4)4221(312)2221(3121=⨯⨯⨯+⨯⨯⨯⨯=+=V V V ;故选D .考点:1.三视图;2.棱锥的体积.3.如图是一个几何体的三视图,则该几何体的体积是( )A .54B .27C .18D .9 【答案】C 【解析】 试题分析:由三视图可知该几何体为四棱锥,底面为矩形,两边为6,3,棱锥的高为3,所以体积为1633183V =⨯⨯⨯= 考点:三视图4.如图, 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积为 ( )A .2B .6C .2(23)+D .2(23)+2+【答案】C 【解析】试题分析:由三视图可知该几何体为四棱锥,底面为正方形,对角线为2,高为2,所以侧面为四个直角三角形,面积为112222622(23)22S =⨯⨯⨯+⨯⨯⨯=+ 考点:三视图及棱锥侧面积5.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .56+12B .60+12C .30+6D .28+6 【答案】C 【解析】试题分析:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,求出各个面的面积,相加可得答案.解:根据题意,还原出如图的三棱锥A ﹣BCD 底面Rt △BCD 中,BC ⊥CD ,且BC=5,CD=4侧面△ABC 中,高AE ⊥BC 于E ,且AE=4,BE=2,CE=3 侧面△ACD 中,AC==5∵平面ABC ⊥平面BCD ,平面ABC∩平面BCD=BC ,AE ⊥BC ∴AE ⊥平面BCD ,结合CD ⊂平面BCD ,得AE ⊥CD ∵BC ⊥CD ,AE∩BC=E∴CD ⊥平面ABC ,结合AC ⊂平面ABC ,得CD ⊥AC 因此,△ADB 中,AB==2,BD==,AD==,∴cos ∠ADB==,得sin ∠ADB==,由三角形面积公式,得S △ADB =×××=6,又∵S △ACB =×5×4=10,S △ADC =S △CBD =×4×5=10 ∴三棱锥的表面积是S 表=S △ADB +S △ADC +S △CBD +S △ACB =30+6,故选:C考点:由三视图求面积、体积.6.如图,'''O A B ∆是水平放置的OAB ∆的直观图,则OAB ∆的面积是( )A .12B .62C .6D .32 【答案】A 【解析】试题分析:根据斜二测画法知OAB ∆为边长6OA =,高2''224OB O B ==⨯=,故OAB ∆的面积是164122S =⨯⨯=.考点:平面图形的直观图.7.已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,则该正方体的正视图的面积等于( )A . 32 B.1 C.212+ D.2【答案】D 【解析】试题分析:因为正方体的棱长为1,俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,说明侧视图是底面对角线为边,正方体的高为一条边的矩形,几何体放置如图:那么正视图的图形与侧视图的图形相同,所以正视图的面积为:2 考点:三视图8.如图,'''Rt O A B ∆是OAB ∆的斜二测直观图,斜边''2O A =,则OAB ∆的面积是( )A .22B .1C .2D .22 【答案】D 【解析】 试题分析:2,90,45,2,O A B A O B O B ''''''''=∠=︒∠=︒∴=2,22,90,OA OB AOB ∴==∠=︒OAB ∴∆的面积为112222222AOB S OA OB ∆=⋅=⨯⨯=,故选D .考点:斜二测画法.【方法点晴】本题要求我们将一个直观图形进行还原,由斜二测画法法则可知原图是一个两边分别在,x y 轴的直角三角形,x 轴上的边长与原图形相等,而y 轴上的边长是原图形边长的一半,由此求出原三角形的面积,本题着重考查了斜二测画法中直观图与原图形面积之间的关系的问题和三角形的面积公式,本题着重考查了斜二测画法和三角形的面积公式,属于基础题.9.如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积是12,则该几何体的俯视图可以是( )【答案】C 【解析】 试题分析: 若俯视图为A ,则几何体为边长为1的正方体,所以体积为1,不满足条件;若为B ,则该几何体为底面直径为1,高为1的圆柱,此时体积为2112π⎛⎫⨯ ⎪⎝⎭14π=,不满足条件;若为D ,几何体为底面半径为1,高为1141144ππ⨯⨯=,不满足条件;若为C ,该几何体为底面是直角三角形且两直角边为1,高为1的三棱柱,所以体积为1112⨯⨯=12,满足条件,所以选C.考点:三视图与几何体的表面积与体积.10.一个锥体的正视图和左视图如下图,下面选项中,不可能是该锥体的俯视图的是( )【答案】C 【解析】试题分析:本题中给出了正视图和左视图,故可以根据正俯同长,左俯同宽来找出正确选项.A 、B 、D 中的视图满足三视图法则;C 中的视图不满足三视图中左俯同宽,故其错误,故选C.考点:三视图的作图规则.11.某四棱锥三视图如图所示,则该四棱锥体积为( )A .B .16C .32D .【答案】D 【解析】试题分析:四棱锥为正四棱锥,底面边长为4,高为2.解:由三视图可知四棱锥为正四棱锥,棱锥的底面边长为4,棱锥的高为2. 所以四棱锥的体积V==.故选:D .考点:由三视图求面积、体积.12.某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A. B. C.6 D.4【答案】A【解析】试题分析:根据三视图,还原成几何体,再根据长度关系,即可求得几何体的体积解:由三视图知,原几何体为一个正方体挖掉一个正四棱锥其中正方体的棱为2,正四棱柱的底面边长为正方体的上底面,高为1∴原几何体的体积为故选A考点:由三视图求面积、体积.13.如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为()A.36 B.9 C.72 D.48【答案】B【解析】试题分析:由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥,进而可得答案.解:由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥,底面面积S=×6×3=9,棱锥的高h=3,故几何体的体积V==9,故选:B考点:由三视图求面积、体积.14.一个空间几何体的三视图如图所示,则该几何体的体积为()A. B. C.40 D.80【答案】A【解析】试题分析:几何体为其中一个侧面在下面的四棱锥,结合直观图判断棱锥的高及底面相关线段的长,把数据代入棱锥的体积公式计算.解:由三视图知:几何体为其中一个侧面在下面的四棱锥,如图:其中SA⊥平面ABCD,SA=4,底面ABCD为直角梯形,且AD=4,BC=1,AB=4,∴几何体的体积V=××4×4=.故选:A.考点:由三视图求面积、体积.15.定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱,将正三棱柱截去一个角,(如图1所示,M,N分别为AB,BC的中点)得到几何体如图2.则该几何体按图2所示方向的侧视图为()A. B.C. D.【答案】B【解析】试题分析:结合几何体的结构特征,利用左视图的定义求解.解:解题时在图2的右边放扇墙(心中有墙),图2所示方向的侧视图,由于平面EMN在平面ADFC上,故侧视图中仍然看到矩形中的两条斜线段,∴该几何体按图2所示方向的侧视图为B.故选:B考点:棱柱的结构特征;简单空间图形的三视图.16.已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为()A.1 B.2 C.3 D.4【答案】D【解析】试题分析:由题意可知,几何体为三棱锥,将其放置在长方体模型中即可得出正确答案.解:由题意可知,几何体是三棱锥,其放置在长方体中形状如图所示(图中红色部分),利用长方体模型可知,此三棱锥的四个面中,全部是直角三角形.故选:D.考点:由三视图还原实物图.17.若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是()A.2cm2B.cm3C.3cm3D.3cm3【答案】B【解析】试题分析:由几何体的三视图得到原几何体的底面积与高,进而得到该几何体的体积.解:由几何体的三视图可知,该几何体为底面是直角梯形,高为的四棱锥,其中直角梯形两底长分别为1和2,高是2.故这个几何体的体积是×[(1+2)×2]×=(cm3).故选:B.考点:由三视图求面积、体积.18.已知一个几何的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为()A.B.4 C.6 D.10【答案】C试题分析:由三视图得该几何体是直三棱柱ABC﹣A1B1C1、三棱锥D﹣ABC和三棱锥D ﹣BCE组合体,其中AD⊥平面ABC,且AD=AC=AB=AA1=2,CE=1,AB⊥AC,由此能求出该几何体的体积.解:由三视图得该几何体是直三棱柱ABC﹣A1B1C1、三棱锥D﹣ABC和三棱锥D﹣BCE组合体,其中AD⊥平面ABC,且AD=AC=AB=AA1=2,CE=1,AB⊥AC∴该几何体的体积:V=+V D﹣ABC+V D﹣DCE=+=6.故选:C.考点:由三视图求面积、体积.19.一几何体的直观图如图所示,下列给出的四个俯视图中正确的是()A.B.C.D.【答案】B【解析】试题分析:通过几何体结合三视图的画图方法,判断选项即可.解:几何体的俯视图,轮廓是矩形,几何体的上部的棱都是可见线段,所以C、D不正确;几何体的上部的棱与正视图方向垂直,所以A不正确,故选:B.考点:简单空间图形的三视图.20.如图所示的直观图的平面图形ABCD是()A.任意梯形B.直角梯形C.任意四边形D.平行四边形【答案】B试题分析:由直观图可知,BC ,AD 两条边与横轴平行且不等,边AB 与纵轴平行,得到AB 与两条相邻的边之间是垂直关系,而另外一条边CD 不和上下两条边垂直,得到平面图形是一个直角梯形.解:根据直观图可知,BC ,AD 两条边与横轴平行且不等, 边AB 与纵轴平行, ∴AB ⊥AD ,AB ⊥BC∴平面图形ABCD 是一个直角梯形, 故选B .考点:平面图形的直观图.21.某饮用水器具的三视图如图所示,则该几何体的表面积为( )A .6πB .8πC .7πD .11π 【答案】C 【解析】试题分析:根据三视图可知,该几何体为圆柱斜切去四分之一得到,并且由于几何体是饮用水用具,没有盖子,所以表面积由两部分组成,底面是圆,侧面是矩形的四分之三,故表面积2312474S πππ=⋅+⋅⋅=. 考点:立体几何三视图——表面积.22.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是( )1俯视图侧视图正视图333A .4B .5C .32D .33 【答案】D 【解析】试题分析:作出直观图如下图所示,通过计算得到最长为2233AF BF AB =+=.31333ABC FEDG考点:立体几何三视图与直观图.23.一个四面体的顶点在空间直角坐标系O xyz中的坐标分别是)0,0,0)(0,1,1)(1,0,1)(1,1,0(,画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为()【答案】A【解析】试题分析:由四个顶点坐标可知四面体的直观图如图1所示,是棱长为1的正方体的一个顶点与其中三个面的中心所围成的,所以以zOx平面为投影面,则得到的正视图如图2.图1图2考点:三视图,投影,空间坐标系.【思路点睛】解答本题,首先要能够根据四个顶点的空间坐标,画出(或者在脑海中想象出)四面体在空间坐标系中的具体位置,由坐标可知点)1,1,0)(1,0,1)(0,1,1(在zOx平面投影坐标分别为)1,0,0)(1,0,1)(0,0,1(,所以正视图应该为正方形,也可以直接根据空间几何图得出投影正视图.24.如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为()A .16π B. C .8π D.4π 【答案】B 【解析】试题分析:仔细观察三视图,很容易得知,此几何体实为一个边长为的正方体经过两次切割而成,两切割都是沿着相对的边所在面进行切割,所以此几何体的外接球实为正方体的外接球,则外接球半径为,所以表面积为,故正确选项为B.考点:三视图,球体表面积.25.某几何体的三视图如图所示, 则该几何体的体积是 ( )A.10B.20C.30D.40 【答案】B 【解析】试题分析:如图,几何体为四棱锥,43==AB AC ,,090=∠BAC ,所以5=BC ,点A 到BC 的距离就是点A 到平面11B BCC 的距离,距离等于512543=⨯,所以三棱锥的体积205125531=⨯⨯⨯=V ,故选B.考点:1.三视图;2.几何体的体积.26.某空间几何体的三视图如图所示,则该几何体的外接球的表面积是( )A.36πB. 52πC. 72πD.100π 【答案】B 【解析】试题分析:由三视图可知,该几何体为如下图所示的三棱柱,其中42AC =,4BD =,所以()2422426AB BC ==+=2O D x =,则224O A O B x ==-,所以()22222(4)x x +=-,解之得1x =,所以223O A O B ==,设三棱柱的外接球半径为R ,则2223213R =+=,外接球的表面积2452S R ππ==,故选B.OD D 1BCA 1C 1B 1AO 1O 2考点:1.三视图;2.球的表面各与体积.【名师点睛】本题主要考查三视图与球的表面积与体积等知识,属中档题;空间几何体的三视图是每年高考的热点,题型为选择题或填空题,难度适中,高考对三视图的考查有以下几个命题角度:1.由几何体的直观图求三视图;2.由几何体的部分视图画出剩余视图;3.由三视图还原出几何体的形状,再求其体积或表面积等相关的问题. 27.某几何体的三视图如图所示,则该几何体的侧面积等于( )A.822+ B .1122+ C .1422+ D .15【答案】A 【解析】试题分析:几何体为上下底面为直角梯形的直四棱柱,梯形的一个腰长为1,另一个腰长为21122=+,所以侧面积为:2282222221+=⨯+⨯+⨯⨯,所以选A .考点:1.几何体的三视图;2.几何体的表面积.28.一个长方体被一个平面截去一部分后所剩几何体的三视图如下图所示(单位:cm ),则该几何体的体积为( )A .1203cmB .803cmC .1003cmD .603cm 【答案】C 【解析】试题分析:由三视图可知,该几何体为如下图所示的几何体,其体积1145645610032V =⨯⨯-⨯⨯⨯⨯=,故选C.BCDB'D'C'A考点:1.三视图;2.多面体的体积与表面积.29.某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是( )A . π12B . π34C .π48D .π332 【答案】B 【解析】 试题分析:由三视图,得该几何体是一个三棱锥,且各顶点都在棱长为2 的正方体上,则该几何体的外接球即为正方体的外接球,则322=R ,即3=R ,则所求外接球的体积为ππ34343==R V ;故选B . 考点:1.三视图;2.球与多面体的组合.30.某几何体的三视图如图所示,则这个几何体的体积为( )A .4B .203 C .263D .8 【答案】B【解析】试题分析:由三视图可得到几何体的直观图如图所示,该几何体是由一个四棱锥A CDEF -和一个三棱锥F ABC -组成,四棱锥A CDEF -的底面面积为4,高为4,所以体积是1164433V =⨯⨯=;三棱锥F ABC -的底面积为2,高为2,故体积是43,所以该几何体的体积为203,故选B.考点:三视图与几何体的体积.【方法点睛】三视图问题几乎是各地的必考题目,通常考查考生的空间想象能力,最常见的题型是结合三视图考查几何体的体积、表面积或其与球的组合体问题.若考查体积,只需要确定几何体的形状,哪是底面,哪是高,根据三视图之间的关系“主俯同长,左俯同宽,主左同高”求出底面积和高,根据各多面体的体积公式即可求解;若研究其表面积往往就需要还原几何体,通常的做法是从一个明显的视图沿相反的方向“拉出”,在利用另外两个几何体进行验证;研究多面体与球的组合体最重要的是确定其与球的关系,确定球心的位置.31.已知某几何体的三视图如图所示,则该几何体的表面积为( )A .37 B .217C .13D .210317+【答案】C【解析】试题分析:由三视图可知几何体为三棱台,作出直观图如图所示,则CC '⊥平面ABC ,上下底均为等腰直角三角形,12AC BC AC BC A C B C C C ⊥==''=''='=,,,∴222AB A B =''=,.∴棱台的上底面积为122111⨯⨯=,下底面积为12222⨯⨯=,梯形ACC A ''的面积为112232⨯+⨯=(),梯形BCC B ''的面积为()112232⨯+⨯=,过A 作AD AC ⊥''于D ,过D 作DE A B ⊥'',则2AD CC ='=,DE 为A B C ∆'''斜边高的12,∴22DE =,∴2232AE AD DE =+=.∴梯形ABB A ''的面积为()122322292⨯+⨯=.∴几何体的表面积123319232S =++++=.故选:C . 考点:由三视图求面积、体积.32.一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为( )A.3+6B.3+5C.2+6D.2+5 【答案】C 【解析】试题分析:由三视图还原为空间几何体,如图所示,则有1 2.OAOB AB ==,= 又22215123PB ABCD PB BD PB AB PD PA ⊥∴⊥⊥∴++平面,,,==,==,从而有222PA DA PD PA DA ∴⊥+=,,∴该几何体的侧面积112212236 2.22S ⨯⨯⨯⨯⨯⨯=+=+ 考点:三视图,几何体的体积33.有一个几何体的三视图如下图所示,这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对 【答案】A 【解析】试题分析:由题为已知三视图来判断几何体的形状。

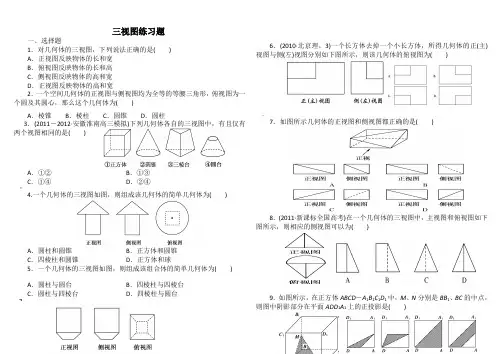
三视图练习题一、选择题1.对几何体的三视图,下列说法正确的是()A.正视图反映物体的长和宽B.俯视图反映物体的长和高C.侧视图反映物体的高和宽D.正视图反映物体的高和宽2.一个空间几何体的正视图与侧视图均为全等的等腰三角形,俯视图为一个圆及其圆心,那么这个几何体为():A.棱锥B.棱柱C.圆锥D.圆柱3.(2011-2012·安徽淮南高三模拟)下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④¥4.一个几何体的三视图如图,则组成该几何体的简单几何体为()A.圆柱和圆锥B.正方体和圆锥C.四棱柱和圆锥D.正方体和球5.一个几何体的三视图如图,则组成该组合体的简单几何体为()A.圆柱与圆台B.四棱柱与四棱台C.圆柱与四棱台D.四棱柱与圆台%6.(2010·北京理,3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为()—7.如图所示几何体的正视图和侧视图都正确的是()8.(2011·新课标全国高考)在一个几何体的三视图中,主视图和俯视图如下图所示,则相应的侧视图可以为()9.如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是BB1、BC的中点,则图中阴影部分在平面ADD1A1上的正投影是()·10.某几何体的三视图如图所示,那么这个几何体是()A.三棱锥B.四棱锥?C.四棱台D.三棱台二、填空题11.下列图形:①三角形;②直线;③平行四边形;④四面体;⑤球.其中投影不可能是线段的是________.^12.(2011·烟台高一检测)已知某一几何体的正视图与侧视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有________.13.(2011-2012·湖南高三“十二校联考”)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为4的正方体.—三、解答题14.如图所示是一个四棱柱铁块,画出它的三视图.15.依所给实物图的形状,画出所给组合体的三视图./16.说出下列三视图表示的几何体:17.根据下列图中所给出的一个物体的三视图,试画出它的形状.|…—~](详解答案1[答案]C2[答案]C3[答案]D[解析]①正方体,三视图均相同;②圆锥,正视图和侧视图相同;③三棱台,三视图各不相同;④圆台,正视图和侧视图相同.[点评]熟悉常见几何体的三视图特征,对于画几何体的直观图是基本的要求.·下图是最基本的常见几何体的三视图.几何体直观图形正视图侧视图俯视图正方体…长方体<圆柱圆锥【圆台球;[解析]由正视图和侧视图可知,该几何体的上部可能为棱锥或圆锥,下部可能为棱柱和圆柱,结合俯视图为圆和圆心及正方形知,上部是圆锥,下部是四棱柱.5[答案]B[解析]该几何体形状如图.上部是一个四棱柱,下部是一个四棱台.;6[答案]C[解析]由正视图和侧视图知,该长方体上面去掉的小长方体,从正前方看在观察者左侧,从左向右看时在观察者右侧,故俯视图为C.7[答案]B8[答案]D[解析]此几何体为一个半圆锥和一个半三棱锥的组合体,只有D项符合题意.9[答案]A[解析]N点投影为AD中点,M点投影为AA1中点,故选A.10[答案]B[解析]由正视图与侧视图知,该几何体为棱锥,由俯视图知,该几何体是四棱锥.11[答案]②④⑤[解析]三角形的投影是线段成三角形;直线的投影是点或直线;平行四边形的投影是线段或平行四边形;四面体的投影是三角形或四边形;球的投影是圆.12[答案]①②③④13[答案]3[解析]该几何体是四棱锥,其底面是边长为4的正方形,高等于4,如图(1)所示的四棱锥A-A1B1C1D1,如图(2)所示,三个相同的四棱锥A-A1B1C1D1,A-BB1C1C,A-DD1C1C可以拼成一个棱长为4的正方体.14[答案]正视图、俯视图、侧视图分别如图所示.15[解析]图中所给几何体是一个圆柱和一个正六棱柱的组合体,在中心以中心轴为轴线挖去一个小圆柱,故其三视图如下:16[解析]17[答案]所对应的空间几何体的图形为:。
2015/08/11
高二数学练习(2)--- 投影与三视图(1)
高二 ( )班 姓名
1.一个几何体的正视图和侧视图都是等腰三角形,俯视图是圆,则这个几何体可能是┄( ) A.圆柱 B.三棱柱 C.圆锥 D.球
2、若一个几何体的正视图是矩形,则这个几何体不可能是┄┄┄┄┄┄┄┄┄┄┄┄( ) A.棱柱 B.棱台 C.圆柱 D.圆锥
3、若如图所示为一简单组合体的三视图,则它的左部分和 右部分是┄┄┄┄┄┄┄┄( )
A.圆锥、圆柱
B.圆柱、圆锥
C.圆柱、圆柱
D.圆锥、圆锥
4、下列几何体各自的三视图中,有且仅有两个视图相同的是
…………………………
.(
)
(
A )① ②
(B
)① ③
(C )① ④
(D )② ④
5、如右图所示的正方体中,M 、N 分别是11,CC AA 的中点,作四边形,1MBN D 则四边形MBN D 1在正方体各个面上的正投影图形中,不可能出现的是( )
D
C
B
A
1
A
6、球的正视图是 ,侧视图是 , 俯视图是 .
7、画出下列几何体的三视图:
侧视图俯视图正视图
①正方体 ②圆锥 ③三棱台 ④正四棱锥
第(2)小题图
8、观察下列几何体的三视图,想象它的几何结构特征,然后画出它的示意图. (1) (2)
9、根据下列描述,说出几何体的结构特征,并画出它们的三视图: (1)由六个面围成,其中一个面是正五边形,其余五个面是
全等的等腰三角形的几何体;
(2)如图,由一个面旋转一周形成的几何体
.
侧视图
主视图。

1.2.1、2 空间几何体的三视图基础巩固一、选择题1.下列投影是平行投影的是()A.俯视图B.路灯底下一个变长的身影C.将书法家的真迹用电灯光投影到墙壁上D.以一只白炽灯为光源的皮影[答案] A[解析]三视图是由平行投影形成的,而B、C、D中由电灯发出的光得到的投影是中心投影.2.对几何体的三视图,下列说法正确的是()A.正视图反映物体的长和宽B.俯视图反映物体的长和高C.侧视图反映物体的高和宽D.正视图反映物体的高和宽[答案] C3.某空间几何体的正视图是三角形,则该几何体不可能是()A.圆柱B.圆锥C.四面体D.三棱柱[答案] A4.小周过生日,公司为她预订的生日蛋糕(示意图)如下图所示,则它的正视图应该是() [答案] B[解析]A为俯视图,注意到封闭的线段情形,正视图应该是B.5.一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台[答案] D[分析]利用三视图逐个排除错误选项即可.[解析]由俯视图可排除A,B,由正视图可排除C,故选D.6.若一个几何体的三视图如下图所示,则这个几何体是()A.三棱锥B.四棱锥C.三棱柱D.四棱柱[答案] B[解析]由俯视图可知底面为四边形,由正视图和侧视图知侧面为三角形,故几何体为四棱锥.二、填空题7.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.[答案]①②③⑤[解析]三棱锥、四棱锥和圆锥的正视图都是三角形,当三棱柱的一个侧面平行于水平面,底面对着观测者时其正视图是三角形,四棱柱、圆柱无论怎样放置,其正视图都不可能是三角形.8.下图中三视图表示的几何体是________.[答案]四棱柱三、解答题9.如图,四棱锥的底面是正方形,顶点在底面上的射影是底面正方形的中心,试画出其三视图.[解析]所给四棱锥的三视图如下图.[点评](1)画三视图时,务必做到正视图与侧视图的高度一致(即所谓的高平齐)、正视图与俯视图的长度一致(即所谓的“长对正”)、侧视图与俯视图的宽度一致(即所谓的“宽相等”).(2)习惯上将侧视图放在正视图的右侧,将俯视图放在正视图的下方.[拓展提高](1)三视图中各种数据的对应关系:①正视图中AB的长对应原四棱锥底面多边形的左右方向的长度,AC、BC的长则不对应侧棱的长,它们对应四棱锥的顶点到底面左、右两边的距离.②侧视图中,EF的长度对应原四棱锥底面的前后长度,GE、GF的长度则是四棱锥顶点与底面前后两边的距离.③俯视图中HIJK的大小与四棱锥底面的大小形状完全一致,而OK,OI,OJ,OH 的大小,则为四棱锥的顶点在底面上的投影到底面各顶点的距离.(2)误区警示:正视图、侧视图中三角形的腰长有的学生会误认为是棱锥的侧棱长,实则不然.弄清一些数据的对应关系,是后面进行相关计算的前提.10.依所给实物图的形状,画出所给组合体的三视图.[解析]图中所给几何体是一个圆柱和一个正六棱柱的组合体,在中心以中心轴为轴线挖去一个小圆柱,故其三视图如下:能力提升一、选择题1.下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④[答案] D[解析]①正方体,三视图均相同;②圆锥,正视图和侧视图相同;③三棱台,三视图各不相同;④圆台,正视图和侧视图相同.[点评]熟悉常见几何体的三视图特征,对于画几何体的直观图是基本的要求.下图是最基本的常见几何体的三视图.几何体直观图形正视图侧视图俯视图正方体长方体圆柱圆锥圆台球[答案] C[分析]本题是组合体的三视图问题,由几何体的正视图和侧视图均如左图所示知,几何体下面为圆柱或直四棱柱,上面是圆柱或直四棱柱或底面是直角三角形的直三棱柱.[解析]A,B,D都可能是该几何体的俯视图,C不可能是该几何体的俯视图,因为它的正视图上面应为如右图所示的矩形.3.如图所示,画出四面体AB1CD1三视图中的正视图,以面AA1D1D为投影面,则得到的正视图可以为()[答案] A[分析]依次确定四面体AB1CD1的每一条棱在面AA1D1D上的投影即可.[解析]显然AB1,AC,B1D1,CD1分别投影得到正视图的外轮廓,B1C为可见实线,AD1为不可见虚线.故A正确.4.若某几何体的三视图如图所示,那么这个几何体是()A.三棱锥B.四棱锥C.四棱台D.三棱台[答案] B[解析]根据三视图的特征可以断定是四棱锥,由正视图和侧视图可知,该四棱锥底面中,必定有一组对边平行,另一组对边不平行.二、填空题5.下列图形:①三角形;②直线;③平行四边形;④四面体;⑤球.其中投影不可能是线段的是________.[答案]②④⑤[解析]三角形的投影是线段或三角形;直线的投影是点或直线;平行四边形的投影是线段或平行四边形;四面体的投影是三角形或四边形;球的投影是圆.6.已知某一几何体的正视图与侧视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有________.[答案]①②③④三、解答题7.说出下列三视图表示的几何体:[解析]8.根据下列图中所给出的一个物体的三视图,试画出它的形状.[答案]所对应的空间几何体的图形为:。
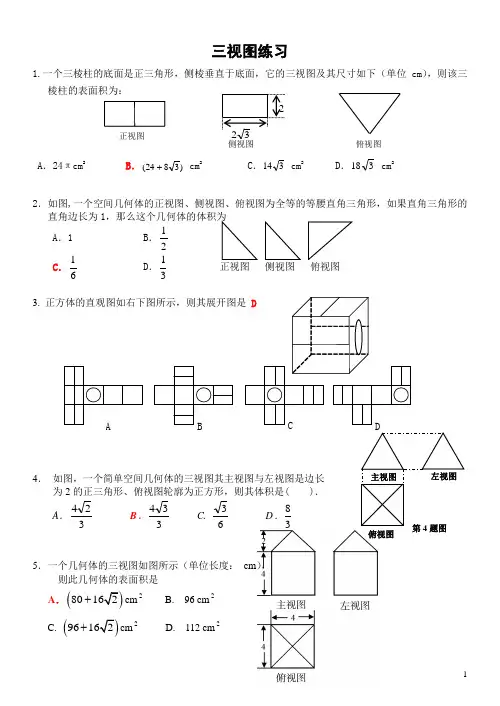
三视图练习1.一个三棱柱的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm ),则该三棱柱的表面积为:A .24πcm 2B.)3824(+ cm 2C .314 cm2D .318 cm22.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1 A .1 B .21C .61D .31正视图 侧视图 俯视图3.4. 为2A .324 B . 334 C. 635.一个几何体的三视图如图所示(单位长度: cm ),则此几何体的表面积是A .(80+cm 2 B. 96 cm 2C. (96+cm2D. 112 cm 2俯视图俯视图俯视图侧视图正视图侧视图正视图6.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为7. 如图,一个空间几何体的主视图和左视图都是边长为1俯视图是一个圆,那么这个几何体的侧面积...为_____2π8.用单位立方块搭一个几何体,使它的主视图和俯视图 如右图所示,则它的体积的最小值与最大值分别为( ) A .9与13 B .7与10 C .10与16 D .10与159.如图所示,甲、乙、丙是三个立方体图形的三视图,甲、乙、丙对应的标号正确的是①长方体 ②圆锥 ③三棱锥 ④圆柱A .④③②B .②①③C .①②③D .③②④10.一个几何体的三视图如图所示,则该几何体的体积等于(A) 8 + 4π3 (B) 4 + 4π3(C) 8 + 4π (D) 10π311.一个几何体的三视图如右图所示,其中正视图 和侧视图是腰长为4的两个全等的等腰直角三角形. 则该几何体的体积是 ;用 3 个这样的(甲)(乙)(丙)主视图左视图俯视图主视图左视图俯视图主视图左视图俯视图左视图 主视图 主视图 俯视图俯视图侧视图正视图侧视图正视图俯视图几何体可以拼成一个棱长为4的正方体.12.已知一几何体的三视图如下,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 ①③④⑤ (写出所有正确结论的编号). ①矩形;②不是矩形的平行四边形;③有三个面为直角三角形,有一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体; ⑤每个面都是直角三角形的四面体.13.如右图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为 (不考虑接触点) A . 6+3+π B . 18+3+π4 C . 18+23+π D . 32+π14.如图,水平放置的三棱柱的侧棱长和底边长均为2, 且侧棱1111AA A B C ⊥面,正视图是边长为2的正方形, 该三棱柱的左视图面积为( ). A. 4B. 32C. 22D.315. 一个空间几何体的正视图、侧视图是两个边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,则这个几何体的体积等于( )A .1B .12C .13 D .1416. 一个几何体的三视图如右图所示(单位长度: cm),A. 2(24cm +B. 2(22cm +正视图 侧视图俯视图_ B _1_ A _1_ B_ A _ B _1 _ A _1 _ B _ A正视图俯视图C. 2(28cm +D. 2(26cm +17.如右图,一个空间几何体的主视图、左视图是周长为4一个内角为060的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为__π______.18.已知某个几何体的三视图如图(主视图中的弧线是半圆), 根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )3cm .A.π+8B.328π+C.π+12D.3212π+19.一个几何体的三视图如图所示,其中正视图与左视图都是边长为2的正三角形,则这个几何体的侧面积为 ( ) A B .2π C .3π D .4π例1 如图,下列物体的正视图和俯视图中有错误的一项是 ( )左视图主视图侧视图主视图俯视图俯视图左(侧)视图正(主)视图例 2 如图所示,甲、乙、丙是三个立体图形的三视图,甲、乙、丙对应的标号正确的是()①长方体;②圆锥;③三棱柱;④圆柱.A.④③②B.②①③C.①②③D.③②④以上两题都是考查最基本的三视图概念. 在理解三视图所表示的几何体中,应有必要的空间想象能力,三视图不仅可以让我们更好地把握空间几何体的性质,而且可以相互转化,即由空间几何体画出三视图,由三视图画出空间几何体,通过这样的转化,进一步培养学生的空间想象能力.斜二侧画法是画几何直观图的基础,在教学过程中,应从实际例子出发,明确画法的原理和法则.例 3 如果平面四边形水平放置直观是一个底角为45 ,腰和上底均为1(下底大于上底)的等腰梯形,那么原平面图形的面积是__________________________________.这是一个不难的问题,只要根据斜二侧画法的法则,即可作出解答,但很多学生在后来碰到这样的问题时,很难理解题目的条件,以至于无法解答,这说明在学习这个画法时就一知半解.高考解答题一般都以几何体作为载体,考查线面间的位置关系,而这个几何体完全可以利用三视图给出,这样不仅要有较好的空间想象能力,而且对三视图的概念应该理解,应用非常熟练,因此在教学过程中必须考虑到这些情况,全面提高学生的数学修养.例4 一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积(单位:cm).这是一个简单的计算题,容易弄错的地方是把图中所标的当作正三棱柱底面边长进行计算,其实是正三棱柱底面三角形的高,这就考查到了三视图的概念,如果再添加点其他元素或关系,则可以作为一个综合题进行考查.。
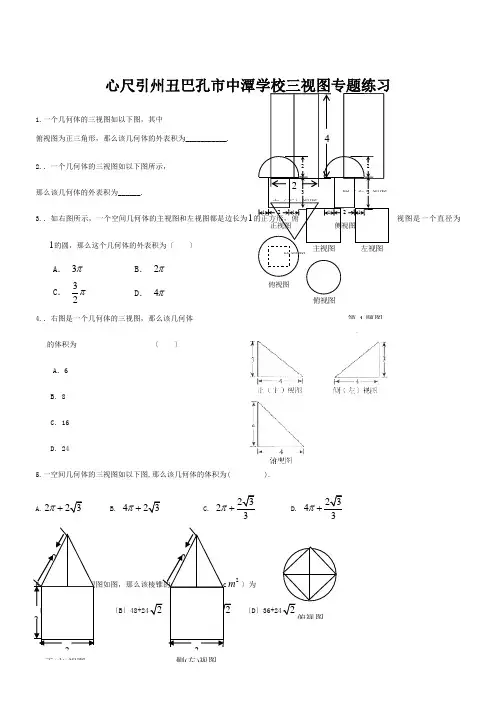
俯视图侧〔左〕视图24主〔正〕视图1.一个几何体的三视图如以下图,其中俯视图为正三角形,那么该几何体的外表积为___________.2..一个几何体的三视图如以下图所示, 那么该几何体的外表积为______.3..如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的外表积为〔〕A . π3B . π2C . π23D . π44..右图是一个几何体的三视图,那么该几何体 的体积为 〔 〕A .6B .8C .16D .245.一空间几何体的三视图如以下图,那么该几何体的体积为( ).A.223π+B. 423π+C. 2323π+D. 2343π6.一个棱锥的三视图如图,那么该棱锥的全面积〔单位:c 2m 〕为 〔A 〕48+122 〔B 〕2 〔C 〕36+122 〔D 〕2正视图侧视图俯视图1223112231第4题图主视图俯视图左视图22正(主)视图 22侧(左)视图7.假设某几何体的三视图〔单位:cm〕如以下图,那么此几何体的体积是3cm.8.设某几何体的三视图如下〔尺寸的长度单位为m〕。
那么该几何体的体积为3m9..如图是一个几何体的三视图,假设它的体积是33,那么=a_______积为12。
那么10.如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体该集合体的俯视图可以是11.右图是一个几何体的三视图,根据图中数据,可得该几何体的外表积是(A)9π〔B〕10π(C)11π (D)12π参考答案:4+234+12π3.A4.B5.C6.A89. 310.C11.D。
三视图一.选择题〔共24小题〕1.一个几何体的三视图如下图,那么这个几何体的体积等于〔〕A.12 B.4 C.D.2.某四面体三视图如下图,那么该四面体的四个面中,直角三角形的面积和是〔〕A.2 B.4 C.D.3.某四面体的三视图如下图,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,那么此四面体的外接球的体积是〔〕A.12πB.48πC.4πD.32π4.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,那么该多面体的各面中,面积最大的是〔〕A.8 B.C.12 D.165.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,那么该几何体的体积为〔〕A.B.C.D.46.某几何体的三视图如下图,那么该几何体的体积为〔〕A.3B.C.D.7.某几何体的三视图如下图,那么该几何体的体积是〔〕A.B.C.D.8.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,那么它的体积为〔〕A.48 B.16 C.32 D.169.某几何体的三视图如下图,那么该几何体的外接球的半径为〔〕A.2B.C.3 D.10.某四棱锥的三视图如下图,其俯视图为等腰直角三角形,那么该四棱锥的体积为〔〕A.B.C.D.411.某三棱锥的三视图如下图,那么该三棱锥的四个面中,面积最大的面的面积是〔〕A.B.C.D.12.如图网格纸上的小正方形边长为1,粗线是一个三棱锥的三视图,那么该三棱锥的外接球外表积为〔〕A.48πB.36πC.24πD.12π13.某几何体的主视图和左视图如图〔1〕,它的俯视图的直观图是矩形O1A1B1C1如图〔2〕,其中O1A1=6,O1C1=2,那么该几何体的侧面积为〔〕A.48 B.64 C.96 D.12814.如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,那么该四面体的外表积为〔〕A.8+8+4B.8+8+2 C.2+2+D.++15.某几何体的三视图如下图,那么该几何体的外表积为〔〕A.7+B.7+2C.4+2D.4+16.如图,网络纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图,那么该几何体的体积为〔〕A.B.2 C.8 D.617.如图,一个几何体的三视图是三个直角三角形,那么该几何体的最长的棱长等于〔〕A.2B.3 C.3 D.918.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,那么该四棱锥的四个侧面中面积最大的一个侧面的面积为〔〕A.8B.8 C.8 D.619.某几何体的三视图如下图,那么该几何体的体积为〔〕A.6 B.8 C.10 D.1220.如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,假设该多面体的所有顶点都在球O外表上,那么球O的外表积是〔〕A.36πB.48πC.56πD.64π21.某几何体的三视图如下图〔单位:cm〕,那么该几何体的体积是〔〕A.4 cm3B.8 cm3C.12 cm3D.24 cm322.一个几何体的三视图如下图,那么该几何体的体积是〔〕A.2 B.6 C.D.23.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,那么在该几何体中,最长的棱与最短的棱所成角的余弦值是〔〕A.B.C.D.24.某几何体三视图如下图,那么该几何体的外接球的外表积为〔〕A.B.12πC.D.2017年04月13日三视图参考答案与试题解析一.选择题〔共24小题〕1.〔2017•一模〕一个几何体的三视图如下图,那么这个几何体的体积等于〔〕A.12 B.4 C.D.【考点】由三视图求面积、体积.【专题】计算题.【分析】该几何体是四棱锥,底面是直角梯形,一条侧棱垂直底面,根据公式可求体积.【解答】解:由三视图复原几何体,如图,它的底面是直角梯形,一条侧棱垂直底面高为2,这个几何体的体积:,应选B.【点评】此题考察三视图、棱锥的体积;考察简单几何体的三视图的运用;培养同学们的空间想象能力和根本的运算能力;是中档题.2.〔2017•荔湾区校级模拟〕某四面体三视图如下图,那么该四面体的四个面中,直角三角形的面积和是〔〕A.2 B.4 C.D.【考点】由三视图求面积、体积.【专题】空间位置关系与距离.【分析】根据三视图复原得到原几何体,分析原几何体可知四个面中直角三角形的个数,求出直角三角形的面积求和即可.【解答】解:由三视图可得原几何体如图,∵PO⊥底面ABC,∴平面PAC⊥底面ABC,而BC⊥AC,∴BC⊥平面PAC,∴BC⊥AC.该几何体的高PO=2,底面ABC为边长为2的等腰直角三角形,∠ACB为直角.所以该几何体中,直角三角形是底面ABC和侧面PBC.PC=,∴,,∴该四面体的四个面中,直角三角形的面积和.应选:C.【点评】此题考察了由三视图复原原图形,考察了学生的空间想象能力和思维能力.3.〔2017•一模〕某四面体的三视图如下图,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,那么此四面体的外接球的体积是〔〕A.12πB.48πC.4πD.32π【考点】由三视图求面积、体积.【专题】计算题;方程思想;综合法;立体几何.【分析】由三视图知该几何体为棱锥,其中SC⊥平面ABCD,此四面体的外接球为正方体的外接球,正方体的对角线长为2,外接球的半径为,即可求出此四面体的外接球的体积.【解答】解:由三视图知该几何体为棱锥S﹣ABD,其中SC⊥平面ABCD,此四面体的外接球为正方体的外接球,正方体的对角线长为2,外接球的半径为所以四面体的外接球的体积=4.应选:C.【点评】此题考察三视图,考察四面体的外接球的体积,确定三视图对应直观图的形状是关键.4.〔2017•模拟〕如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,那么该多面体的各面中,面积最大的是〔〕A.8 B.C.12 D.16【考点】由三视图求面积、体积.【专题】计算题;函数思想;转化思想;空间位置关系与距离.【分析】根据三视图得出该几何体是在棱长为4的正方体中的三棱锥,画出图形,求出各个面积即可.【解答】解:根据题意,得;该几何体是如下图的三棱锥A﹣BCD,且该三棱锥是放在棱长为4的正方体中,所以,在三棱锥A﹣BCD中,BD=4,AC=AB==,AD==6,S△ABC=×4×4=8.S△ADC==4,S△DBC=×4×4=8,在三角形ABC中,作CE⊥E,连结DE,那么CE==,DE==,S△ABD==12.应选:C.【点评】此题考察了空间几何体三视图的应用问题,解题的关键是由三视图复原为几何体,是中档题.5.〔2017•二模〕如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,那么该几何体的体积为〔〕A.B.C.D.4【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】如下图,由三视图可知该几何体为:四棱锥P﹣ABCD.【解答】解:如下图,由三视图可知该几何体为:四棱锥P﹣ABCD.连接BD.其体积V=V B﹣PAD+V B﹣PCD==.应选:B.【点评】此题考察了正方体与四棱锥的三视图、体积计算公式,考察了推理能力与计算能力,属于中档题.6.〔2017•二模〕某几何体的三视图如下图,那么该几何体的体积为〔〕A.3B.C.D.【考点】由三视图求面积、体积.【专题】综合题;转化思想;演绎法;空间位置关系与距离.【分析】由三视图可得,几何体为底面为正视图,高为的四棱锥,即可求出几何体的体积.【解答】解:由三视图可得,几何体为底面为正视图,高为的四棱锥,体积为=,应选B.【点评】此题考察由三视图求面积、体积,考察学生的计算能力,确定几何体的形状是关键.7.〔2017•一模〕某几何体的三视图如下图,那么该几何体的体积是〔〕A.B.C.D.【考点】由三视图求面积、体积.【专题】数形结合;数形结合法;立体几何.【分析】根据三视图作出几何体的直观图,将几何体分解成两个棱锥计算体积.【解答】解:做出几何体的直观图如下图:其中底面ABCD是边长为2的正方形,AE,DF为底面的垂线,且AE=2,DF=1,∴V=V E﹣ABC+V C﹣ADFE=+=.应选D.【点评】此题考察了空间几何体的三视图,体积计算,属于中档题.8.〔2017•一模〕如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,那么它的体积为〔〕A.48 B.16 C.32 D.16【考点】由三视图求面积、体积.【专题】选作题;数形结合;分割补形法;立体几何.【分析】根据三视图画出此几何体:镶嵌在正方体中的四棱锥,由正方体的位置关系判断底面是矩形,做出四棱锥的高后,利用线面垂直的判定定理进展证明,由等面积法求出四棱锥的高,利用椎体的体积公式求出答案.【解答】解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O﹣ABCD,正方体的棱长为4,O、A、D分别为棱的中点,∴OD=2,AB=DC=OC=2,做OE⊥CD,垂足是E,∵BC⊥平面ODC,∴BC⊥OE、BC⊥CD,那么四边形ABCD是矩形,∵CD∩BC=C,∴OE⊥平面ABCD,∵△ODC的面积S==6,∴6==,得OE=,∴此四棱锥O﹣ABCD的体积V===16,应选:B.【点评】此题考察三视图求不规那么几何体的体积,以及等面积法的应用,由三视图正确复原几何体、并放在对应的正方体中是解题的关键,考察空间想象能力和数形结合思想.9.〔2017•一模〕某几何体的三视图如下图,那么该几何体的外接球的半径为〔〕A.2B.C.3 D.【考点】由三视图求面积、体积.【专题】计算题;数形结合;空间位置关系与距离;立体几何.【分析】由中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,进而得到答案.【解答】解:由中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,故2R==2,故R=,应选:B【点评】三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,此题考察了学生的空间想象力,识图能力及计算能力.10.〔2017•和平区校级模拟〕某四棱锥的三视图如下图,其俯视图为等腰直角三角形,那么该四棱锥的体积为〔〕A.B.C.D.4【考点】由三视图求面积、体积.【专题】综合题;方程思想;演绎法;空间位置关系与距离.【分析】由三视图知:几何体为四棱锥,且四棱锥的高为,底面是边长为2,矩形,把数据代入锥体的体积公式计算.【解答】解:由三视图知:几何体为四棱锥,且四棱锥的高为,底面是边长为2,矩形,∴几何体的体积V==.应选B.【点评】此题考察了由三视图求几何体的体积,判断几何体的形状及数据所对应的几何量是关键.11.〔2017•海淀区模拟〕某三棱锥的三视图如下图,那么该三棱锥的四个面中,面积最大的面的面积是〔〕A.B.C.D.【考点】由三视图求面积、体积.【专题】综合题;数形结合法;立体几何.【分析】根据几何体的三视图知该几何体是三棱锥,由三视图求出几何体的棱长、并判断出线面的位置关系,由勾股定理、余弦定理、三角形的面积公式求出各个面的面积,即可得几何体的各面中面积最大的面的面积.【解答】解:根据几何体的三视图知,该几何体是三棱锥P﹣ABC,直观图如下图:由图得,PA⊥平面ABC,,,,,那么,在△PBC中,,由余弦定理得:,那么,所以,所以三棱锥中,面积最大的面是△PAC,其面积为,应选B.【点评】此题考察由三视图求几何体的外表积,勾股定理、余弦定理、三角形的面积公式的应用,由三视图正确复原几何体是解题的关键,考察空间想象能力.12.〔2017春•南安市校级月考〕如图网格纸上的小正方形边长为1,粗线是一个三棱锥的三视图,那么该三棱锥的外接球外表积为〔〕A.48πB.36πC.24πD.12π【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】由中的三视图可得,该几何体的外接球,相当于一个棱长为2的正方体的外接球,即可得出.【解答】解:由中的三视图可得,该几何体的外接球,相当于一个棱长为2的正方体的外接球,故外接球直径2R=2,故该三棱锥的外接球的外表积S=4πR2=12π,应选:D.【点评】此题考察了正方体与三棱锥的三视图、球的外表积计算公式,考察了推理能力与计算能力,属于中档题.13.〔2016•校级二模〕某几何体的主视图和左视图如图〔1〕,它的俯视图的直观图是矩形O1A1B1C1如图〔2〕,其中O1A1=6,O1C1=2,那么该几何体的侧面积为〔〕A.48 B.64 C.96 D.128【考点】由三视图求面积、体积.【专题】计算题;数形结合;综合法;空间位置关系与距离;立体几何.【分析】由中的三视图可得该几何体是一个四棱柱,计算出底面的周长和高,进而可得几何体的侧面积.【解答】解:由中的三视图可得该几何体是一个四棱柱,∵它的俯视图的直观图是矩形O1A1B1C1,O1A1=6,O1C1=2,∴它的俯视图的直观图面积为12,∴它的俯视图的面积为:24,∴它的俯视图的俯视图是边长为:6的菱形,棱柱的高为4故该几何体的侧面积为:4×6×4=96,应选:C.【点评】此题考察的知识点是由三视图,求体积和外表积,根据的三视图,判断几何体的形状是解答的关键.14.〔2016•校级模拟〕如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,那么该四面体的外表积为〔〕A.8+8+4B.8+8+2 C.2+2+D.++【考点】由三视图求面积、体积.【专题】数形结合;数形结合法;立体几何.【分析】由三视图可知几何体为从边长为4的正方体切出来的三棱锥.作出直观图,计算各棱长求面积.【解答】解:由三视图可知几何体为从边长为4的正方体切出来的三棱锥A﹣BCD.作出直观图如下图:其中A,C,D为正方体的顶点,B为正方体棱的中点.∴S△ABC==4,S△BCD==4.∵AC=4,AC⊥CD,∴S△ACD==8,由勾股定理得AB=BD==2,AD=4.∴cos∠ABD==﹣,∴sin∠ABD=.∴S△ABD==4.∴几何体的外表积为8+8+4.应选A.【点评】此题考察了不规那么放置的几何体的三视图和面积计算,作出直观图是解题关键.15.〔2016•校级三模〕某几何体的三视图如下图,那么该几何体的外表积为〔〕A.7+B.7+2C.4+2D.4+【考点】由三视图求面积、体积.【专题】计算题;数形结合;数形结合法;立体几何.【分析】几何体为从正方体中切出来的三棱锥,利用正方体模型计算三棱锥的各边,再计算面积.【解答】解:由三视图可知几何体为从边长为2正方体中切出来的三棱锥A﹣BCD,如下图.其中C为正方体棱的中点,∴S△ABC==2,S ABD==2,∵AC=BC==,∴S△ACD==.∵CD==3,BD=2,∴cos∠CBD==.∴sin∠CBD=.∴S△BCD==3.∴几何体的外表积S=2+2++3=7+.应选A.【点评】此题考察了不规那么放置的几何体的三视图及面积计算,作出直观图是解题关键.16.〔2016•模拟〕如图,网络纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图,那么该几何体的体积为〔〕A.B.2 C.8 D.6【考点】由三视图求面积、体积.【专题】计算题;数形结合;综合法;立体几何.【分析】直观图如下图,底面为梯形,面积为=3,四棱锥的高为2,即可求出几何体的体积.【解答】解:直观图如下图,底面为梯形,面积为=3,四棱锥的高为2,∴几何体的体积为=2,应选:B.【点评】此题考察几何体的体积,考察学生的计算能力,确定直观图的形状是关键.17.〔2016•校级模拟〕如图,一个几何体的三视图是三个直角三角形,那么该几何体的最长的棱长等于〔〕A.2B.3 C.3 D.9【考点】由三视图求面积、体积.【专题】数形结合;分析法;空间位置关系与距离.【分析】由三视图知该几何体是一个三棱锥,由三视图求出几何元素的长度、判断出线面的位置关系,由图判断出几何体的最长棱,由勾股定理求出即可.【解答】解:由三视图知几何体是一个三棱锥P﹣ABC,直观图如下图:PC⊥平面ABC,PC=1,且AB=BC=2,AB⊥BC,∴AC=,∴该几何体的最长的棱是PA,且PA==3,应选:B.【点评】此题考察几何体的三视图,由三视图正确复原几何体是解题的关键,考察空间想象能力.18.〔2016•四模〕如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,那么该四棱锥的四个侧面中面积最大的一个侧面的面积为〔〕A.8B.8 C.8 D.6【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.S-ABCD【分析】根据三视图可得此棱锥的高为SO=4,底面为直角梯形,且CD=AB=2,AB∥CD,且ABCO 为正方形,如下图,根据数据即可得出.【解答】解:根据三视图可得此棱锥的高为SO=4,底面为直角梯形,且CD=AB=2,AB∥CD,且ABCO为正方形,如下图:故该四棱锥的四个侧面中面积最大的一个侧面为SCB或SAB,它的面积为CB•SC=×4×4=8,应选:B.【点评】此题考察了三视图的有关计算、四棱锥的侧面积计算公式,考察了推理能力与计算能力,属于中档题.19.〔2016•模拟〕某几何体的三视图如下图,那么该几何体的体积为〔〕A.6 B.8 C.10 D.12【考点】由三视图求面积、体积.【专题】计算题;转化思想;综合法;立体几何.【分析】由三视图得到几何体为三棱柱去掉一个三棱锥,分别计算体积即可.【解答】解:由三视图得到几何体如图体积为=10;应选C.【点评】此题考察了由三视图求几何体的体积;关键是正确复原几何体形状,根据公式计算体积.20.〔2016•二模〕如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,假设该多面体的所有顶点都在球O外表上,那么球O的外表积是〔〕A.36πB.48πC.56πD.64π【考点】由三视图求面积、体积;球的体积和外表积.【专题】综合题;数形结合;分割补形法;解三角形;空间位置关系与距离.【分析】根据三视图知几何体是三棱锥为棱长为4的正方体一局部,画出直观图,由正方体的性质求出球心O到平面ABC的距离d、边AB和AC的值,在△ABC中,由余弦定理求出cos∠ACB后,求出∠ACB和sin∠ACB,由正弦定理求出△ABC的外接圆的半径r,由勾股定理求出球O的半径,由球的外表积公式求解.【解答】解:根据三视图知几何体是:三棱锥D﹣ABC为棱长为4的正方体一局部,直观图如下图:∵该多面体的所有顶点都在球O,且球心O是正方体的中心,∴由正方体的性质得,球心O到平面ABC的距离d=2,由正方体的性质可得,AB=BD==,AC=,设△ABC的外接圆的半径为r,在△ABC中,由余弦定理得,cos∠ACB===,∴∠ACB=45°,那么sin∠ACB=,由正弦定理可得,2r===2,那么r=,即球O的半径R==,∴球O的外表积S=4πR2=56π,应选:C.【点评】此题考察三视图求几何体外接球的外表积,正弦定理、余弦定理,以及正方体的性质,结合三视图和对应的正方体复原几何体是解题的关键,考察空间想象能力.21.〔2016•二模〕某几何体的三视图如下图〔单位:cm〕,那么该几何体的体积是〔〕A.4 cm3B.8 cm3C.12 cm3D.24 cm3【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】由三视图可知:该几何体是一个四棱锥.P﹣ABCD,侧面PAB⊥底面ABCD,底面ABCD是一个直角梯形.【解答】解:由三视图可知:该几何体是一个四棱锥.P﹣ABCD,侧面PAB⊥底面ABCD,底面ABCD是一个直角梯形.∴该几何体的体积=×2=4cm3.应选:A.【点评】此题考察了三视图的有关计算、四棱锥的体积计算公式,考察了推理能力与计算能力,属于中档题.22.〔2016•模拟〕一个几何体的三视图如下图,那么该几何体的体积是〔〕A.2 B.6 C.D.【考点】由三视图求面积、体积.【专题】数形结合;转化思想;综合法;空间位置关系与距离.【分析】由三视图可知:该几何题是由一个三棱锥截取一个三棱锥剩下的几何体.【解答】解:由三视图可知:该几何题是由一个三棱锥截取一个三棱锥剩下的几何体.∴该几何体的体积=﹣=2.应选:A.【点评】此题考察了三视图的有关计算、三棱锥与四棱锥的体积计算公式,考察了推理能力与计算能力,属于中档题.23.〔2016•一模〕如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,那么在该几何体中,最长的棱与最短的棱所成角的余弦值是〔〕A.B.C.D.【考点】由三视图求面积、体积.【专题】数形结合;数形结合法;立体几何.【分析】由三视图知该几何体是一个四棱柱P﹣ABCD,由三视图求出几何元素的长度、并判断出位置关系,从而可得最短、最长的棱长以及长度,由图和余弦定理求出答案.【解答】解:根据三视图可知几何体是一个四棱柱P﹣ABCD,且底面是直角梯形,AB⊥AD、AD∥CB,且AB=BC=4、AD=2,PA⊥平面ABCD,PA=4,由图可得,最短的棱是AD=2,最长的侧棱长是PC====4,且PB=,∵AD∥BC,∴最长的棱PC与最短的棱AD所成角是∠PCB,在直角三角形PBC中,cos∠PCB===,应选:D.【点评】此题考察几何体的三视图,由三视图正确复原几何体是解题的关键,考察空间想象能力.24.〔2016春•兴国县校级月考〕某几何体三视图如下图,那么该几何体的外接球的外表积为〔〕A.B.12πC.D.【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】由三视图知:几何体为三棱锥S﹣ABC,且三棱锥的一个侧面SAC垂直于底面ABC,高SD=2,AD=DC=1.如图:△ABC的外接圆的圆心为斜边AC的中点E,设该几何体的外接球的球心为O.OE⊥底面ABC,设OE=x,外接球的半径为R,利用勾股定理即可得出.【解答】解:由三视图知:几何体为三棱锥S﹣ABC,且三棱锥的一个侧面SAC垂直于底面ABC,高SD=2,AD=DC=1.底面为等腰直角三角形,直角边长为2,如图:∴△ABC的外接圆的圆心为斜边AC的中点E,设该几何体的外接球的球心为O.OE⊥底面ABC,设OE=x,外接球的半径为R,那么=1+〔2﹣x〕2,〔OA2=OS2〕解得x=.∴R2=,∴外接球的外表积S=4π×R2=.故答案为:.【点评】此题考察了三棱锥的三视图、空间位置关系、外接球的性质、勾股定理,考察了推理能力与计算能力,属于中档题.。
高二数学空间几何体的三视图和直观图试题1.如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为()A.B.4C.D.【答案】D【解析】因为,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1底面ABC,其正(主)视图是边长为2的正方形,所以,该三棱柱为正三棱柱,其柱侧(左)视图为矩形,一条边长为2,另一条边长为正三角形的高,故此三棱柱侧(左)视图的面积为,选D。
【考点】本题主要考查三视图,直三棱柱的几何特征,面积计算。
点评:基础题,三视图是高考必考题目,因此,要明确三视图视图规则。
三视图视图过程中,要注意虚线的出现,意味着有被遮掩的棱。
2.一个正三棱柱的三视图如图所示,则这个正三棱柱的侧面积为A.B.C.D.【答案】D【解析】由三视图可知:原几何体为正三棱柱,其中底面三角形的高为3,三棱柱的高为2,所以底面三角形的的边长为,所以这个三棱柱的侧面积。
【考点】三视图;棱柱的侧面积公式。
点评:正确还原几何体及正确还原几何体的棱长是做此类题的关键。
属于常见且基础题型。
3.若某多面体的三视图(单位:cm)如下图所示,则此多面体的体积是()A.cm3B. cm3C.cm3D.cm3【答案】D【解析】解:由三视图可知该几何体为上部是一平放的直五棱柱,柱体高h=1.侧视图为其底面.底面多边形可看作边长为1的正方形截去直角边为1 2 的等腰直角三角形而得到,其面积S=1×1-1 2 ×× =所以几何体体积V=Sh=1× =故答案为D4.若某空间几何体的三视图如图所示,则该几何体的体积是A.1B.2C.D.【答案】A【解析】此几何体是一个平躺的三棱柱,所以其体积为.5.一空间几何体的三视图如图所示,则该几何体的体积为( )A.B.C.D.【答案】C【解析】由三视图判断空间几何体是由下圆柱和上四棱锥组成,并根据三视图求出圆柱的半径和高,四棱锥的边长和高,代入对应的体积公式分别求解,最后再和在一起并且圆柱的底面半径为1,高为2,体积为2π,四棱锥的底面边长为,高为,体积为1 /3 •( )2•=所以该几何体的体积为2π+6.一个体积为的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为()A.B.8C.D.12【答案】少图【解析】略7.右图是长和宽分别相等的两个矩形。
专题21 三视图1.某几何体的三视图如图所示,则其表面积为()A.2π B.3π C.4π D.5π【答案】B点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A. B. C. D.【答案】B【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2AB BD AD ===,当BC ABD ⊥平面时, BC=2, ABD ∆的边AB 上的高为3,只有B 选项符合,当BC 不垂直平面ABD 时,没有符合条件的选项,故选B .点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为( )A . 4B . 22C .203D . 8 【答案】D4.如图,正三棱柱111ABC A B C -的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为( )A . 16B . 23C . 43D . 83【答案】D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.5.某几何体的三视图如图所示,则该几何体的体积为 ( )(A) 168π+ (B) 88π+ (C) 1616π+ (D) 816π+【答案】A【解析】将三视图还原为原来的几何体,再利用体积公式求解.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示),其体积为21422241682V ππ=⨯⨯+⨯⨯=+.故选A;6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) 62 (B) 42 (C) 6 (D)4【答案】C【解析】如图所示点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为( )A . 24π-B . 24π+C . 20π-D . 20π+【答案】A8.已知某空间几何体的三视图如图所示,则该几何体的表面积是()A. B. C. D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴,,,,∴,故选A.9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )A .1π+B .2π+C .21π+D .3522π++【答案】A【解析】考点:由三视图求体积.10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A .263π+B .83π+C .243π+D .43π+【答案】C【解析】试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.考点:三视图.11.一个几何体的三视图如图所示,则该几何体的体积为()A.143B. 5 C.163D.6【答案】A【解析】考点:三视图.12.一个几何体的三视图如图所示,则该几何体的体积为____.【答案】1 3【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为1111133V=⨯⨯⨯=.业主在物业管理中的权利和义务《物业管理条例》规定业主在物业管理中享有的10项权利:一、是按照物业服务合同的约定,接受物业管理企业提供的服务。
高二数学三视图专项练习一.选择题〔共24小题〕1.一个几何体的三视图如图所示,则这个几何体的体积等于〔〕A.12 B.4 C.D.2.某四面体三视图如图所示,则该四面体的四个面中,直角三角形的面积和是〔〕A.2 B.4 C.D.3.某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是〔〕A.12πB.48πC.4πD.32π4.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是〔〕A.8 B.C.12 D.165.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为〔〕A.B.C.D.46.某几何体的三视图如图所示,则该几何体的体积为〔〕A.3 B.C.D.7.已知某几何体的三视图如图所示,则该几何体的体积是〔〕A.B.C.D.8.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为〔〕A.48 B.16 C.32 D.169.某几何体的三视图如图所示,则该几何体的外接球的半径为〔〕A.2 B.C.3 D.10.某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为〔〕A.B.C.D.411.某三棱锥的三视图如图所示,则该三棱锥的四个面中,面积最大的面的面积是〔〕A.B.C.D.12.如图网格纸上的小正方形边长为1,粗线是一个三棱锥的三视图,则该三棱锥的外接球表面积为〔〕A.48πB.36πC.24πD.12π13.某几何体的主视图和左视图如图〔1〕,它的俯视图的直观图是矩形O1A1B1C1如图〔2〕,其中O1A1=6,O1C1=2,则该几何体的侧面积为〔〕A.48 B.64 C.96 D.12814.如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为〔〕A.8+8+4 B.8+8+2 C.2+2+ D.++15.某几何体的三视图如图所示,则该几何体的表面积为〔〕A.7+ B.7+2 C.4+2 D.4+16.如图,网络纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图,则该几何体的体积为〔〕A.B.2 C.8 D.617.如图,一个几何体的三视图是三个直角三角形,则该几何体的最长的棱长等于〔〕A.2 B.3 C.3 D.918.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,则该四棱锥的四个侧面中面积最大的一个侧面的面积为〔〕A.8 B.8 C.8 D.619.某几何体的三视图如图所示,则该几何体的体积为〔〕A.6 B.8 C.10 D.1220.如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,若该多面体的所有顶点都在球O表面上,则球O的表面积是〔〕A.36πB.48πC.56πD.64π21.某几何体的三视图如图所示〔单位:cm〕,则该几何体的体积是〔〕A.4 cm3 B.8 cm3 C.12 cm3 D.24 cm322.一个几何体的三视图如图所示,则该几何体的体积是〔〕A.2 B.6 C.D.23.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱与最短的棱所成角的余弦值是〔〕A.B.C.D.24.某几何体三视图如图所示,则该几何体的外接球的表面积为〔〕A.B.12πC.D.2017年04月13日三视图参考答案与试题解析一.选择题〔共24小题〕1.〔2017•江西一模〕一个几何体的三视图如图所示,则这个几何体的体积等于〔〕A.12 B.4 C.D.【考点】由三视图求面积、体积.【专题】计算题.【分析】该几何体是四棱锥,底面是直角梯形,一条侧棱垂直底面,根据公式可求体积.【解答】解:由三视图复原几何体,如图,它的底面是直角梯形,一条侧棱垂直底面高为2,这个几何体的体积:,故选B.【点评】本题考查三视图、棱锥的体积;考查简单几何体的三视图的运用;培养同学们的空间想象能力和基本的运算能力;是中档题.2.〔2017•荔湾区校级模拟〕某四面体三视图如图所示,则该四面体的四个面中,直角三角形的面积和是〔〕A.2 B.4 C.D.【考点】由三视图求面积、体积.【专题】空间位置关系与距离.【分析】根据三视图还原得到原几何体,分析原几何体可知四个面中直角三角形的个数,求出直角三角形的面积求和即可.【解答】解:由三视图可得原几何体如图,∵PO⊥底面ABC,∴平面PAC⊥底面ABC,而BC⊥AC,∴BC⊥平面PAC,∴BC⊥AC.该几何体的高PO=2,底面ABC为边长为2的等腰直角三角形,∠ACB为直角.所以该几何体中,直角三角形是底面ABC和侧面PBC.PC=,∴,,∴该四面体的四个面中,直角三角形的面积和.故选:C.【点评】本题考查了由三视图还原原图形,考查了学生的空间想象能力和思维能力.3.〔2017•岳阳一模〕某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是〔〕A.12πB.48πC.4πD.32π【考点】由三视图求面积、体积.【专题】计算题;方程思想;综合法;立体几何.【分析】由三视图知该几何体为棱锥,其中SC⊥平面ABCD,此四面体的外接球为正方体的外接球,正方体的对角线长为2,外接球的半径为,即可求出此四面体的外接球的体积.【解答】解:由三视图知该几何体为棱锥S﹣ABD,其中SC⊥平面ABCD,此四面体的外接球为正方体的外接球,正方体的对角线长为2,外接球的半径为所以四面体的外接球的体积=4.故选:C.【点评】本题考查三视图,考查四面体的外接球的体积,确定三视图对应直观图的形状是关键.4.〔2017•本溪模拟〕如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是〔〕A.8 B.C.12 D.16【考点】由三视图求面积、体积.【专题】计算题;函数思想;转化思想;空间位置关系与距离.【分析】根据三视图得出该几何体是在棱长为4的正方体中的三棱锥,画出图形,求出各个面积即可.【解答】解:根据题意,得;该几何体是如图所示的三棱锥A﹣BCD,且该三棱锥是放在棱长为4的正方体中,所以,在三棱锥A﹣BCD中,BD=4,AC=AB==,AD==6,S△ABC=×4×4=8.S△ADC==4,S△DBC=×4×4=8,在三角形ABC中,作CE⊥E,连结DE,则CE==,DE==,S△ABD==12.故选:C.【点评】本题考查了空间几何体三视图的应用问题,解题的关键是由三视图还原为几何体,是中档题.5.〔2017•河北二模〕如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为〔〕A.B.C.D.4【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】如图所示,由三视图可知该几何体为:四棱锥P﹣ABCD.【解答】解:如图所示,由三视图可知该几何体为:四棱锥P﹣ABCD.连接BD.其体积V=VB﹣PAD+VB﹣PCD==.故选:B.【点评】本题考查了正方体与四棱锥的三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.6.〔2017•许昌二模〕某几何体的三视图如图所示,则该几何体的体积为〔〕A.3 B.C.D.【考点】由三视图求面积、体积.【专题】综合题;转化思想;演绎法;空间位置关系与距离.【分析】由三视图可得,几何体为底面为正视图,高为的四棱锥,即可求出几何体的体积.【解答】解:由三视图可得,几何体为底面为正视图,高为的四棱锥,体积为=,故选B.【点评】本题考查由三视图求面积、体积,考查学生的计算能力,确定几何体的形状是关键.7.〔2017•甘肃一模〕已知某几何体的三视图如图所示,则该几何体的体积是〔〕A.B.C.D.【考点】由三视图求面积、体积.【专题】数形结合;数形结合法;立体几何.【分析】根据三视图作出几何体的直观图,将几何体分解成两个棱锥计算体积.【解答】解:做出几何体的直观图如图所示:其中底面ABCD是边长为2的正方形,AE,DF为底面的垂线,且AE=2,DF=1,∴V=VE﹣ABC+VC﹣ADFE=+=.故选D.【点评】本题考查了空间几何体的三视图,体积计算,属于中档题.8.〔2017•钦州一模〕如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为〔〕A.48 B.16 C.32 D.16【考点】由三视图求面积、体积.【专题】选作题;数形结合;分割补形法;立体几何.【分析】根据三视图画出此几何体:镶嵌在正方体中的四棱锥,由正方体的位置关系判断底面是矩形,做出四棱锥的高后,利用线面垂直的判定定理进行证明,由等面积法求出四棱锥的高,利用椎体的体积公式求出答案.【解答】解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O﹣ABCD,正方体的棱长为4,O、A、D分别为棱的中点,∴OD=2,AB=DC=OC=2,做OE⊥CD,垂足是E,∵BC⊥平面ODC,∴BC⊥OE、BC⊥CD,则四边形ABCD是矩形,∵CD∩BC=C,∴OE⊥平面ABCD,∵△ODC的面积S==6,∴6==,得OE=,∴此四棱锥O﹣ABCD的体积V===16,故选:B.【点评】本题考查三视图求不规则几何体的体积,以及等面积法的应用,由三视图正确复原几何体、并放在对应的正方体中是解题的关键,考查空间想象能力和数形结合思想.9.〔2017•蚌埠一模〕某几何体的三视图如图所示,则该几何体的外接球的半径为〔〕A.2 B.C.3 D.【考点】由三视图求面积、体积.【专题】计算题;数形结合;空间位置关系与距离;立体几何.【分析】由已知中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,进而得到答案.【解答】解:由已知中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,故2R==2,故R=,故选:B【点评】三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.10.〔2017•和平区校级模拟〕某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为〔〕A.B.C.D.4【考点】由三视图求面积、体积.【专题】综合题;方程思想;演绎法;空间位置关系与距离.【分析】由三视图知:几何体为四棱锥,且四棱锥的高为,底面是边长为2,矩形,把数据代入锥体的体积公式计算.【解答】解:由三视图知:几何体为四棱锥,且四棱锥的高为,底面是边长为2,矩形,∴几何体的体积V==.故选B.【点评】本题考查了由三视图求几何体的体积,判断几何体的形状及数据所对应的几何量是关键.11.〔2017•海淀区模拟〕某三棱锥的三视图如图所示,则该三棱锥的四个面中,面积最大的面的面积是〔〕A.B.C.D.【考点】由三视图求面积、体积.【专题】综合题;数形结合法;立体几何.【分析】根据几何体的三视图知该几何体是三棱锥,由三视图求出几何体的棱长、并判断出线面的位置关系,由勾股定理、余弦定理、三角形的面积公式求出各个面的面积,即可得几何体的各面中面积最大的面的面积.【解答】解:根据几何体的三视图知,该几何体是三棱锥P﹣ABC,直观图如图所示:由图得,PA⊥平面ABC,,,,,则,在△PBC中,,由余弦定理得:,则,所以,所以三棱锥中,面积最大的面是△PAC,其面积为,故选B.【点评】本题考查由三视图求几何体的表面积,勾股定理、余弦定理、三角形的面积公式的应用,由三视图正确复原几何体是解题的关键,考查空间想象能力.12.〔2017春•南安市校级月考〕如图网格纸上的小正方形边长为1,粗线是一个三棱锥的三视图,则该三棱锥的外接球表面积为〔〕A.48πB.36πC.24πD.12π【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】由已知中的三视图可得,该几何体的外接球,相当于一个棱长为2的正方体的外接球,即可得出.【解答】解:由已知中的三视图可得,该几何体的外接球,相当于一个棱长为2的正方体的外接球,故外接球直径2R=2,故该三棱锥的外接球的表面积S=4πR2=12π,故选:D.【点评】本题考查了正方体与三棱锥的三视图、球的表面积计算公式,考查了推理能力与计算能力,属于中档题.13.〔2016•南昌校级二模〕某几何体的主视图和左视图如图〔1〕,它的俯视图的直观图是矩形O1A1B1C1如图〔2〕,其中O1A1=6,O1C1=2,则该几何体的侧面积为〔〕A.48 B.64 C.96 D.128【考点】由三视图求面积、体积.【专题】计算题;数形结合;综合法;空间位置关系与距离;立体几何.【分析】由已知中的三视图可得该几何体是一个四棱柱,计算出底面的周长和高,进而可得几何体的侧面积.【解答】解:由已知中的三视图可得该几何体是一个四棱柱,∵它的俯视图的直观图是矩形O1A1B1C1,O1A1=6,O1C1=2,∴它的俯视图的直观图面积为12,∴它的俯视图的面积为:24,∴它的俯视图的俯视图是边长为:6的菱形,棱柱的高为4故该几何体的侧面积为:4×6×4=96,故选:C.【点评】本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.14.〔2016•福建校级模拟〕如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为〔〕A.8+8+4 B.8+8+2 C.2+2+ D.++【考点】由三视图求面积、体积.【专题】数形结合;数形结合法;立体几何.【分析】由三视图可知几何体为从边长为4的正方体切出来的三棱锥.作出直观图,计算各棱长求面积.【解答】解:由三视图可知几何体为从边长为4的正方体切出来的三棱锥A﹣BCD.作出直观图如图所示:其中A,C,D为正方体的顶点,B为正方体棱的中点.∴S△ABC==4,S△BCD==4.∵AC=4,AC⊥CD,∴S△ACD==8,由勾股定理得AB=BD==2,AD=4.∴cos∠ABD==﹣,∴sin∠ABD=.∴S△ABD==4.∴几何体的表面积为8+8+4.故选A.【点评】本题考查了不规则放置的几何体的三视图和面积计算,作出直观图是解题关键.15.〔2016•包头校级三模〕某几何体的三视图如图所示,则该几何体的表面积为〔〕A.7+ B.7+2 C.4+2 D.4+【考点】由三视图求面积、体积.【专题】计算题;数形结合;数形结合法;立体几何.【分析】几何体为从正方体中切出来的三棱锥,利用正方体模型计算三棱锥的各边,再计算面积.【解答】解:由三视图可知几何体为从边长为2正方体中切出来的三棱锥A﹣BCD,如图所示.其中C为正方体棱的中点,∴S△ABC==2,SABD==2,∵AC=BC==,∴S△ACD==.∵CD==3,BD=2,∴cos∠CBD==.∴sin∠CBD=.∴S△BCD==3.∴几何体的表面积S=2+2++3=7+.故选A.【点评】本题考查了不规则放置的几何体的三视图及面积计算,作出直观图是解题关键.16.〔2016•福建模拟〕如图,网络纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图,则该几何体的体积为〔〕A.B.2 C.8 D.6【考点】由三视图求面积、体积.【专题】计算题;数形结合;综合法;立体几何.【分析】直观图如图所示,底面为梯形,面积为=3,四棱锥的高为2,即可求出几何体的体积.【解答】解:直观图如图所示,底面为梯形,面积为=3,四棱锥的高为2,∴几何体的体积为=2,故选:B.【点评】本题考查几何体的体积,考查学生的计算能力,确定直观图的形状是关键.17.〔2016•吉林校级模拟〕如图,一个几何体的三视图是三个直角三角形,则该几何体的最长的棱长等于〔〕A.2 B.3 C.3 D.9【考点】由三视图求面积、体积.【专题】数形结合;分析法;空间位置关系与距离.【分析】由三视图知该几何体是一个三棱锥,由三视图求出几何元素的长度、判断出线面的位置关系,由图判断出几何体的最长棱,由勾股定理求出即可.【解答】解:由三视图知几何体是一个三棱锥P﹣ABC,直观图如图所示:PC⊥平面ABC,PC=1,且AB=BC=2,AB⊥BC,∴AC=,∴该几何体的最长的棱是PA,且PA==3,故选:B.【点评】本题考查几何体的三视图,由三视图正确复原几何体是解题的关键,考查空间想象能力.18.〔2016•开封四模〕如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,则该四棱锥的四个侧面中面积最大的一个侧面的面积为〔〕A.8 B.8 C.8 D.6【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.S-ABCD【分析】根据三视图可得此棱锥的高为SO=4,底面为直角梯形,且CD=AB=2,AB∥CD,且ABCO为正方形,如图所示,根据数据即可得出.【解答】解:根据三视图可得此棱锥的高为SO=4,底面为直角梯形,且CD=AB=2,AB∥CD,且ABCO为正方形,如图所示:故该四棱锥的四个侧面中面积最大的一个侧面为SCB或SAB,它的面积为CB•SC=×4×4=8,故选:B.【点评】本题考查了三视图的有关计算、四棱锥的侧面积计算公式,考查了推理能力与计算能力,属于中档题.19.〔2016•湖北模拟〕某几何体的三视图如图所示,则该几何体的体积为〔〕A.6 B.8 C.10 D.12【考点】由三视图求面积、体积.【专题】计算题;转化思想;综合法;立体几何.【分析】由三视图得到几何体为三棱柱去掉一个三棱锥,分别计算体积即可.【解答】解:由三视图得到几何体如图体积为=10;故选C.【点评】本题考查了由三视图求几何体的体积;关键是正确还原几何体形状,根据公式计算体积.20.〔2016•丹东二模〕如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,若该多面体的所有顶点都在球O表面上,则球O的表面积是〔〕A.36πB.48πC.56πD.64π【考点】由三视图求面积、体积;球的体积和表面积.【专题】综合题;数形结合;分割补形法;解三角形;空间位置关系与距离.【分析】根据三视图知几何体是三棱锥为棱长为4的正方体一部分,画出直观图,由正方体的性质求出球心O到平面ABC的距离d、边AB和AC的值,在△ABC中,由余弦定理求出cos∠ACB后,求出∠ACB和sin∠ACB,由正弦定理求出△ABC的外接圆的半径r,由勾股定理求出球O的半径,由球的表面积公式求解.【解答】解:根据三视图知几何体是:三棱锥D﹣ABC为棱长为4的正方体一部分,直观图如图所示:∵该多面体的所有顶点都在球O,且球心O是正方体的中心,∴由正方体的性质得,球心O到平面ABC的距离d=2,由正方体的性质可得,AB=BD==,AC=,设△ABC的外接圆的半径为r,在△ABC中,由余弦定理得,cos∠ACB===,∴∠ACB=45°,则sin∠ACB=,由正弦定理可得,2r===2,则r=,即球O的半径R==,∴球O的表面积S=4πR2=56π,故选:C.【点评】本题考查三视图求几何体外接球的表面积,正弦定理、余弦定理,以及正方体的性质,结合三视图和对应的正方体复原几何体是解题的关键,考查空间想象能力.21.〔2016•嘉兴二模〕某几何体的三视图如图所示〔单位:cm〕,则该几何体的体积是〔〕A.4 cm3 B.8 cm3 C.12 cm3 D.24 cm3【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】由三视图可知:该几何体是一个四棱锥.P﹣ABCD,侧面PAB⊥底面ABCD,底面ABCD是一个直角梯形.【解答】解:由三视图可知:该几何体是一个四棱锥.P﹣ABCD,侧面PAB⊥底面ABCD,底面ABCD是一个直角梯形.∴该几何体的体积=×2=4cm3.故选:A.【点评】本题考查了三视图的有关计算、四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.22.〔2016•洛阳模拟〕一个几何体的三视图如图所示,则该几何体的体积是〔〕A.2 B.6 C.D.【考点】由三视图求面积、体积.【专题】数形结合;转化思想;综合法;空间位置关系与距离.【分析】由三视图可知:该几何题是由一个三棱锥截取一个三棱锥剩下的几何体.【解答】解:由三视图可知:该几何题是由一个三棱锥截取一个三棱锥剩下的几何体.∴该几何体的体积=﹣=2.故选:A.【点评】本题考查了三视图的有关计算、三棱锥与四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.23.〔2016•鹰潭一模〕如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱与最短的棱所成角的余弦值是〔〕A.B.C.D.【考点】由三视图求面积、体积.【专题】数形结合;数形结合法;立体几何.【分析】由三视图知该几何体是一个四棱柱P﹣ABCD,由三视图求出几何元素的长度、并判断出位置关系,从而可得最短、最长的棱长以及长度,由图和余弦定理求出答案.【解答】解:根据三视图可知几何体是一个四棱柱P﹣ABCD,且底面是直角梯形,AB⊥AD、AD∥CB,且AB=BC=4、AD=2,PA⊥平面ABCD,PA=4,由图可得,最短的棱是AD=2,最长的侧棱长是PC====4,且PB=,∵AD∥BC,∴最长的棱PC与最短的棱AD所成角是∠PCB,在直角三角形PBC中,cos∠PCB===,故选:D.【点评】本题考查几何体的三视图,由三视图正确复原几何体是解题的关键,考查空间想象能力.24.〔2016春•兴国县校级月考〕某几何体三视图如图所示,则该几何体的外接球的表面积为〔〕A.B.12πC.D.【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】由三视图知:几何体为三棱锥S﹣ABC,且三棱锥的一个侧面SAC垂直于底面ABC,高SD=2,AD=DC=1.如图:△ABC的外接圆的圆心为斜边AC的中点E,设该几何体的外接球的球心为O.OE⊥底面ABC,设OE=x,外接球的半径为R,利用勾股定理即可得出.【解答】解:由三视图知:几何体为三棱锥S﹣ABC,且三棱锥的一个侧面SAC垂直于底面ABC,高SD=2,AD=DC=1.底面为等腰直角三角形,直角边长为2,如图:∴△ABC的外接圆的圆心为斜边AC的中点E,设该几何体的外接球的球心为O.OE⊥底面ABC,设OE=x,外接球的半径为R,则=1+〔2﹣x〕2,〔OA2=OS2〕解得x=.。