第4章 自变量中含有定性变量的回归分析

回归分析：探索变量之间的关系引言回归分析是统计学中一种常用的数据分析方法，用于探索变量之间的关系。

它可以帮助我们理解一个或多个自变量对因变量的影响程度，并预测未来的结果。

本文将介绍回归分析的基本概念、原理和应用，以及常见的回归模型和评估方法。

第一章：回归分析的基本概念1.1 回归分析的定义回归分析是统计学中一种用于研究变量之间关系的方法。

它通过建立一个数学模型，描述自变量和因变量之间的关系，并利用数据对模型进行估计和预测。

1.2 回归分析的作用回归分析可以用于解决许多实际问题，例如预测销售额、评估市场需求、分析经济趋势等。

它可以帮助我们理解变量之间的关系，并提供决策依据。

第二章：回归分析的原理2.1 线性回归模型线性回归模型是回归分析中最常用的模型之一。

它假设自变量和因变量之间存在线性关系，并通过最小二乘法来估计模型的参数。

线性回归模型的数学表达式为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε，其中Y表示因变量，X1、X2、...、Xn表示自变量，β0、β1、β2、...、βn表示模型的参数，ε表示误差项。

2.2 模型的参数估计为了估计模型的参数，我们需要使用样本数据。

通过最小二乘法，我们可以最小化观测值与模型预测值之间的差异，从而得到最优的参数估计。

2.3 模型的拟合度模型的拟合度可以通过判定系数（R²）来评估。

判定系数表示模型预测值与实际观测值之间的相关程度，取值范围为0到1。

当判定系数接近1时，说明模型能够很好地解释观测值的变异；当判定系数接近0时，说明模型的解释能力较弱。

第三章：回归模型的应用3.1 单变量线性回归单变量线性回归是回归分析中最简单的模型。

它只包含一个自变量和一个因变量，可以用于探索两个变量之间的关系。

例如，我们可以使用单变量线性回归模型来研究温度与销售额之间的关系。

3.2 多变量线性回归多变量线性回归是回归分析中常用的模型之一。

它可以用于研究多个自变量对因变量的影响。

报告中的变量选择和回归分析方法引言：报告中的变量选择和回归分析方法是数据分析和统计学中的重要内容。

在研究报告和学术论文中，合理选择变量和进行回归分析可以有效地揭示变量之间的关系，提高分析的准确性和可靠性。

本文将从六个方面对报告中的变量选择和回归分析方法进行详细论述。

一、变量选择的意义变量选择是指在进行回归分析时，从众多可能的自变量中选择出最为重要和相关的变量。

合理的变量选择可以减少冗余变量的存在，避免数据过拟合问题，并提高模型的预测能力和可解释性。

变量选择的意义在于提高研究的效率和有效性。

二、变量选择的方法1. 相关系数法：通过计算自变量与因变量之间的相关系数，选择与因变量关系最为密切的自变量。

相关系数法既简单又直观，但在多变量分析中无法考虑到变量之间的相互作用。

2. 正向选择法：从众多可能的自变量中，逐步添加具有显著影响力的变量，并根据模型的显著性检验去除不显著的变量。

正向选择法可以一步步剔除不相关的变量，但可能会错过一些有用的变量。

3. 逆向选择法：从包含所有自变量的模型开始，逐步去除不显著的变量，直到剩下的自变量都显著。

逆向选择法可以保留所有可能有用的变量，但可能出现模型过于复杂的问题。

三、回归分析的基本原理回归分析是通过建立数学模型，分析自变量对因变量的影响程度和方向。

常见的回归分析方法包括线性回归、多元回归、逻辑回归等。

回归分析需要满足一些基本的假设和前提，如线性关系、多元正态分布等。

四、回归分析的评价指标回归分析的结果需要进行评价，以判断模型的拟合程度和可靠性。

常用的评价指标包括判定系数（R平方）、均方根误差（RMSE）、残差等。

这些指标可以帮助研究者判断模型的准确性，并进行模型的改进和优化。

五、回归分析的解读和应用回归分析的结果需要进行解读，以揭示自变量与因变量之间的关系。

解读回归系数可以确定变量之间的正负相关关系，判断自变量对因变量的影响程度。

回归分析的应用广泛，可以用于预测、控制和优化等多个领域。

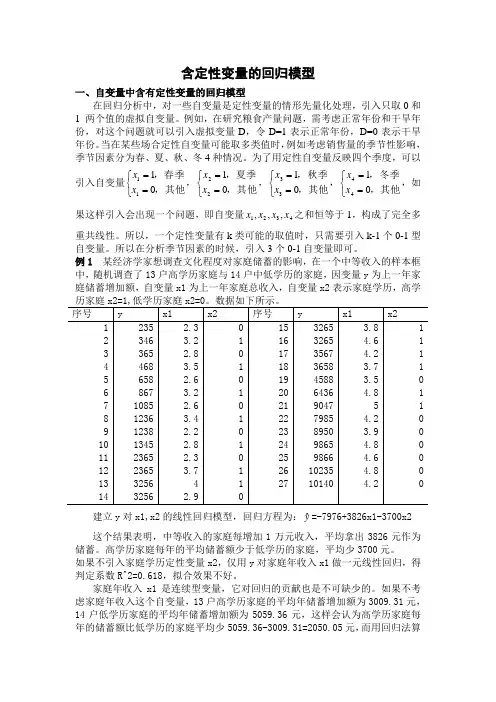
含定性变量的回归模型一、自变量中含有定性变量的回归模型在回归分析中，对一些自变量是定性变量的情形先量化处理，引入只取0和1 两个值的虚拟自变量。

例如，在研究粮食产量问题，需考虑正常年份和干旱年份，对这个问题就可以引入虚拟变量D ，令D=1表示正常年份，D=0表示干旱年份。

当在某些场合定性自变量可能取多类值时，例如考虑销售量的季节性影响，季节因素分为春、夏、秋、冬4种情况。

为了用定性自变量反映四个季度，可以引入自变量⎩⎨⎧==，其他，春季0111x x ，⎩⎨⎧==，其他，夏季0122x x ，⎩⎨⎧==，其他，秋季0133x x ，⎩⎨⎧==，其他，冬季0144x x ，如果这样引入会出现一个问题，即自变量4321,,,x x x x 之和恒等于1，构成了完全多重共线性。

所以，一个定性变量有k 类可能的取值时，只需要引入k-1个0-1型自变量。

所以在分析季节因素的时候，引入3个0-1自变量即可。

例1 某经济学家想调查文化程度对家庭储蓄的影响，在一个中等收入的样本框中，随机调查了13户高学历家庭与14户中低学历的家庭，因变量y 为上一年家庭储蓄增加额，自变量x1为上一年家庭总收入，自变量x2表示家庭学历，高学建立y 对x1,x2的线性回归模型，回归方程为：yˆ=-7976+3826x1-3700x2 这个结果表明，中等收入的家庭每增加1万元收入，平均拿出3826元作为储蓄。

高学历家庭每年的平均储蓄额少于低学历的家庭，平均少3700元。

如果不引入家庭学历定性变量x2，仅用y 对家庭年收入x1做一元线性回归，得判定系数R^2=0.618，拟合效果不好。

家庭年收入x1是连续型变量，它对回归的贡献也是不可缺少的。

如果不考虑家庭年收入这个自变量，13户高学历家庭的平均年储蓄增加额为3009.31元，14户低学历家庭的平均年储蓄增加额为5059.36元，这样会认为高学历家庭每年的储蓄额比低学历的家庭平均少5059.36-3009.31=2050.05元，而用回归法算出的数值是3824元，两者并不相等。

回归分析法概念及原理回归分析是一种统计学方法，用于研究变量之间的关系，并用这些关系来预测或解释一个或多个因变量。

它可以帮助我们理解自变量与因变量之间的线性关系，并根据这种关系进行预测和解释。

回归分析的核心原理是建立一个线性方程来描述自变量和因变量之间的关系。

这个线性方程也称为回归方程。

回归方程的一般形式如下：Y=β0+β1X1+β2X2+...+βkXk+ε其中，Y表示因变量，X1、X2、..、Xk表示自变量，β0、β1、β2、..、βk表示模型的系数，ε表示误差项。

回归方程中，自变量的系数β表示因变量在自变量变化一个单位时的变化量。

例如，假设自变量为X1，系数β1为2，那么当X1增加1个单位时，因变量Y将增加2个单位。

回归分析的目标是通过拟合回归方程来估计模型的系数，并使用这些系数进行预测或解释。

常用的回归分析方法有最小二乘法和最大似然估计法。

最小二乘法是一种常用的回归估计方法。

它通过最小化实际观测值与回归方程预测值之间的误差平方和，来确定最佳的回归系数。

最小二乘法的优点是计算简单，并且能够提供估计系数的置信区间和显著性检验。

最大似然估计法是另一种常用的回归估计方法。

它通过寻找使得观测值出现的概率最大的回归系数来进行估计。

最大似然估计法的优点是可以处理更加复杂的模型，并且提供了参数的置信区间和假设检验。

在进行回归分析之前，需要满足一些基本的假设。

其中最重要的是线性性和正态性假设。

线性性假设指的是自变量和因变量之间的关系是线性的，正态性假设则指的是误差项ε服从正态分布。

在回归分析中，还需要评估模型的拟合优度。

常用的指标包括决定系数（R-squared）和调整决定系数（adjusted R-squared）。

决定系数表示回归方程对因变量变异的解释程度，取值范围从0到1，越接近1表示模型的拟合优度越好。

调整决定系数则对变量的个数进行了修正，避免过拟合。

回归分析有很多应用领域，例如经济学、社会学、生物学和工程学等。

定量分析方法之回归分析回归分析是定量分析的一种重要方法，用于研究两个或多个变量之间的关系。

它可以用来预测一个变量（因变量）如何随着其他变量（自变量）的变化而变化。

回归分析可以帮助我们理解这些变量之间的关系，以及预测未来的数据。

在本文中，我将详细介绍回归分析的原理、应用和如何进行回归分析。

回归分析的原理是建立一个数学模型来描述因变量和自变量之间的关系。

最常用的回归分析方法是线性回归分析，其中假设因变量与自变量之间存在线性关系。

也就是说，我们可以用一条直线来拟合数据，使得预测值与观察值之间的误差最小化。

我们可以用以下的数学模型来描述线性回归分析：Y=β0+β1X+ε，其中Y是因变量，X是自变量，β0和β1是回归系数，ε是误差项。

回归系数可以通过最小二乘法来估计，最小化误差平方和。

我们可以根据回归方程中的回归系数来解释自变量对因变量的影响。

回归分析可以应用于各种问题，包括经济学、金融学、市场营销、社会科学等。

例如，在经济学中，我们可以使用回归分析来研究GDP与就业率、通胀率之间的关系。

在市场营销中，我们可以使用回归分析来预测产品销售量与广告支出之间的关系。

回归分析还可以应用于预测未来的数据，例如预测股价、天气等。

进行回归分析的关键步骤包括数据收集、模型建立、模型评估和结果解释。

首先，我们需要收集数据，包括因变量和自变量的观察值。

然后，我们可以使用统计软件（如R、Python等）来建立回归模型。

在模型建立过程中，我们需要选择适当的自变量、确定回归形式（线性、非线性等）并评估模型的拟合程度。

模型评估通常包括计算回归系数、检验统计显著性和解释方差等。

最后，我们可以使用回归模型来解释结果，并进行预测和决策。

虽然线性回归是最常用的回归分析方法，但也有其他类型的回归模型可以应用于非线性关系，如多项式回归、逻辑回归、岭回归等。

这些模型在应对不同类型的数据和问题时具有更大的灵活性。

总之，回归分析是一种强大的定量分析方法，可以帮助我们理解和预测变量之间的关系。

回归分析知识点总结一、回归分析的基本概念1.1 回归分析的概念回归分析是一种通过数学模型建立自变量与因变量之间关系的方法。

该方法可以用来预测数据、解释变量之间的关系以及发现隐藏的模式。

1.2 回归分析的类型回归分析主要可以分为线性回归和非线性回归两种类型。

线性回归是指因变量和自变量之间的关系是线性的，而非线性回归则是指因变量和自变量之间的关系是非线性的。

1.3 回归分析的应用回归分析广泛应用于各个领域，例如经济学、金融学、生物学、医学等。

在实际应用中，回归分析可以用于市场预测、风险管理、医疗诊断、环境监测等方面。

二、回归分析的基本假设2.1 线性关系假设线性回归分析假设因变量和自变量之间的关系是线性的，即因变量的变化是由自变量的变化引起的。

2.2 正态分布假设回归分析假设误差项服从正态分布，即残差在各个预测点上是独立同分布的。

2.3 同方差假设回归分析假设误差项的方差是恒定的，即误差项的方差在不同的自变量取值上是相同的。

2.4 独立性假设回归分析假设自变量和误差项之间是独立的，即自变量的变化不受误差项的影响。

三、回归分析的模型建立3.1 简单线性回归模型简单线性回归模型是最基础的回归分析模型，它只包含一个自变量和一个因变量，并且自变量与因变量之间的关系是线性的。

3.2 多元线性回归模型多元线性回归模型包含多个自变量和一个因变量，它可以更好地描述多个因素对因变量的影响。

3.3 非线性回归模型当因变量和自变量之间的关系不是线性的时候，可以使用非线性回归模型对其进行建模。

非线性回归模型可以更好地捕捉因变量和自变量之间的复杂关系。

四、回归分析的模型诊断4.1 线性回归模型的拟合优度拟合优度是评价线性回归模型预测能力的指标，它可以用来衡量模型对数据的拟合程度。

4.2 回归系数的显著性检验在回归分析中，通常需要对回归系数进行显著性检验，以确定自变量对因变量的影响是否显著。

4.3 多重共线性检验多重共线性是指自变量之间存在高度相关性，这可能导致回归系数估计不准确。

利用回归分析探究变量间的关系回归分析是一种常用的统计方法，用于研究变量之间的关系。

通过回归分析，我们可以确定一个或多个自变量对因变量的影响程度，并建立数学模型来预测因变量的取值。

本文将介绍回归分析的基本原理，以及如何使用回归分析来探究变量间的关系。

一、回归分析的基本原理回归分析是一种建立因变量与自变量之间关系的统计模型的方法。

它基于一组观测数据，通过拟合一个数学模型来研究变量之间的关系。

回归分析的基本原理包括以下几个方面：1. 回归模型的选择：在进行回归分析之前，我们首先需要选择一个合适的回归模型。

常用的回归模型包括线性回归模型、多项式回归模型、逻辑回归模型等。

选择模型时需要考虑数据的性质和研究的目的。

2. 拟合模型：选择好回归模型后，我们需要通过计算来确定模型的参数。

拟合模型的过程通常采用最小二乘法，即寻找一组参数使得观测数据与模型预测值之间的残差平方和最小。

3. 模型评估：拟合好模型后，我们需要对模型进行评估，主要包括检验模型的显著性、拟合优度以及模型的预测能力等。

二、回归分析的应用案例回归分析在各个领域都有广泛的应用。

下面以实际案例来介绍回归分析在探究变量间关系方面的应用。

案例：销售额与广告投入之间的关系某电商平台想要了解广告投入对销售额的影响，他们收集了一段时间内的广告投入与销售额的数据。

他们使用回归分析来研究这两个变量之间的关系。

在这个案例中，广告投入是自变量，销售额是因变量。

通过回归分析，他们得到了如下的线性回归模型：销售额 = 1000 + 2 * 广告投入根据回归模型的拟合结果，可以解读出广告投入每增加1单位，销售额将增加2单位。

此外，他们还可以利用这个模型来预测不同广告投入下的销售额。

三、回归分析的局限性及注意事项尽管回归分析是一种常用的统计方法，但也存在一些局限性和注意事项，下面列举几点：1. 数据的质量：回归分析对数据的质量有一定要求，数据应当是完整、准确、可靠的。

同时还需要注意是否存在异乎寻常的离群值和异常值。

第四讲含定性自变量的回归模型与联立方程模型一、含定性自变量的回归模型1、定性变量（虚拟变量）的概念一般的线性回归模型变量取值都有具体数值，然而实际问题中经常会碰到这样一些变量，如性别、职称、历史时期（计划经济或市场经济）等，它们不是用数值度量的，被称为定性变量。

含有定性变量的线性回归问题可分为自变量含定性变量和因变量含定性变量两种情况，由于后者比较复杂，有兴趣的同学可以自学。

我们这里只讨论含定性自变量的情况。

2、Eviews的操作解释变量中含有定性变量的问题比较简单。

Eviews的操作步骤与一般多元线性回归模型的建模过程基本相同，只需将定性变量看做一般数值变量操作即可。

而且含定性自变量的回归模型，其各种检验与一般线性回归模型相同。

例：为研究采取某项保险革新措施的速度Y对保险公司的规模X1和保险公司类型的关系，选取下列数据：Y是第i个公司采纳该项革新在时间上间隔的月数；X1是公司的总资产额（单位：百万美元）;X2是一个定性变量，表示公司类型，其中1表示股份公司，0表示互助公司。

数据资料见下表：二、联立方程模型 1、联立方程模型的概述联立方程模型至少含有两个待估计的方程，其一般形式为：(,,)t t t f y x βε=，1,2,,t T = 。

式中，t y 是t 时刻的内生变量向量；t x 是t 时刻的外生变量向量；β是待估计的未知参数向量，t ε是t 时刻的随机扰动项；T 表示样本的容量。

联立方程模型可能包含没有未知参数和扰动项的恒等方程，它们本身并不需要进行估计，但会作为一部分信息与其他方程一起参与整个模型的求解和分析。

联立方程模型有结构式模型与简化式模型，由于对联立方程结构模型参数直接进行OLS 估计会出现联立方程的偏倚，因此对联立方程结构模型的参数进行估计的基本思路是：把结构模型→简化模型→估计简化模型的参数→求解结构模型的参数（唯一解、多个解、无解）。

这种解的不同情况就是联立方程的识别问题。