1- (1 i)-n PA A i
补充1:折现率的计算
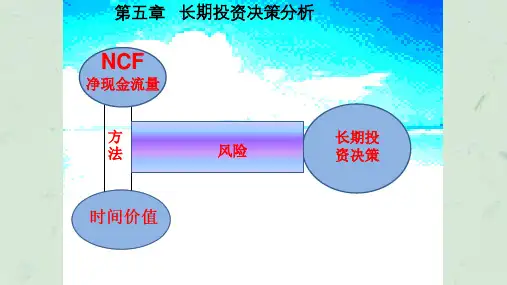
在资金时间价值的计算公式中,都有四个变量, 其中的三个值,就可以推算出第四个的值。前 面讨论的是终值S、现值P以及年金A的计算。 这里讨论的是终值或现值、年金、期间,求折 现率;或者终值或现值、年金、折现率,求期 间。————内插法〔插值法〕
2021/5/25
【例题】F公司正在考虑购置一个新的价 值为925 000元的基于计算机的订单响应 系统。按税法规定,这个设备将在5年内 按照直线折旧法无残值折旧。设备寿命为 5年,在5年末的时候,该设备的市场价值 为90 000元。
2021/5/25
应用该系统后每年可节省税前360 000元的订 单处理本钱,而且,该设备可以一次性节省 125 000元的营运资本投资。F公司适用的所 得税税率为35%,工程资本本钱为10%。 要求:计算该工程每年的税后现金净流量。
〔3〕有效年利率,也叫实际利率,是指 按给定的期间利率每年复利m次时,能够 产生一样结果的年利率,也称等价年利率。
补充3:连续复利问题 1、如果每年复利次数m趋近于无 穷,那么这种情况下的复利称为 “连续复利〞。
2、连续复利情况下的有效年利率
3、连续复利情况下复利终值和现值 计算。假设期数为t,那么:
〔2〕递延年金终值 递延年金终值的大小与递延期无关,因此 其计算与普通年金终值计算根本一样。从 图可知,递延年金终值的计算公式为:
〔3〕递延年金现值的第一种方法: 把递延年金视作n-m期普通年金,求 出递延年金在第m期期末的现值,然 后将此现值折算到第一期期初,用公 式表示为:
PA A (P/A,i,n - m) (P/F,i,m)
【例·计算题】现在向银行存入20 000元,问年利率i为多少 时,才能保证在以后9年中每年年末可以取出4 000元。