陷波器设计

基于lms的自适应陷波器的设计与实现下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!基于LMS的自适应陷波器的设计与实现1. 引言自适应信号处理技术在滤波器设计中具有重要应用，特别是在抑制干扰信号方面表现出色。

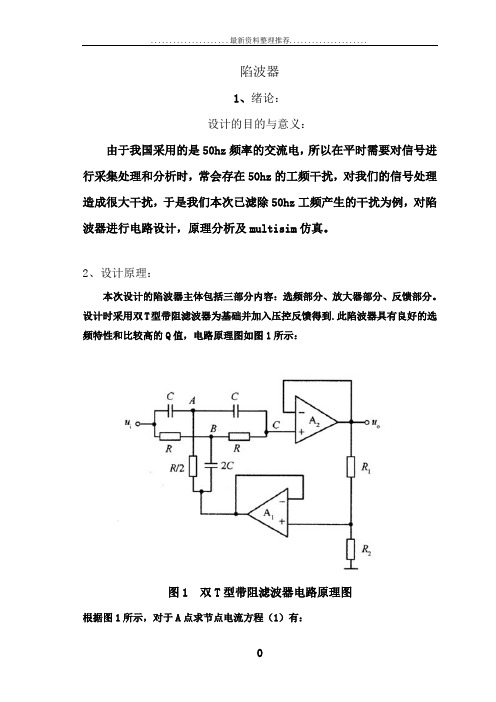
陷波器1、绪论：设计的目的与意义：由于我国采用的是50hz频率的交流电，所以在平时需要对信号进行采集处理和分析时，常会存在50hz的工频干扰，对我们的信号处理造成很大干扰，于是我们本次已滤除50hz工频产生的干扰为例，对陷波器进行电路设计，原理分析及multisim仿真。

2、设计原理：本次设计的陷波器主体包括三部分内容：选频部分、放大器部分、反馈部分。

设计时采用双T型带阻滤波器为基础并加入压控反馈得到.此陷波器具有良好的选频特性和比较高的Q值，电路原理图如图1所示：图1 双T型带阻滤波器电路原理图根据图1所示，对于A点求节点电流方程（1）有：()()()0200=-+-+-n U mU sC U U sC U U A A A i（1）同样，对于B 点求节点电流方程（2）有： ()()()000=-+-+-sC U mU n U U n U U B B B i（2）同样，对于C 点有节点电流方程（3）： ()()00B 0A =-+-n U U sC U U(3) 式中212R R R m +=，R n 1=。

由上述的（1）、（2）、（3）式可以得到此电路的传输函数为()()C n s m s C n s snC m C s n C s n U U s G i -+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=-+++==14C n 14)(22222222220 此时令ωj =s 得ωωωωωωω0202202)1(4)(G m j j ----=其中RC 10=ω。

当0ωω=时）（ωj G =0，此时能滤除RCf π210=的频率，而对于其他频率，）（ωj G 约为1，能很好的使其他频率的信号通过。

令）（ωj G =0.707得到两个截止频率为： ()⎥⎦⎤⎢⎣⎡-+-+=)1(214120m m f f H ()⎥⎦⎤⎢⎣⎡---+=)1(214120L m m f f 此时可以得到陷波器的带宽BW 和其Q 值0)1(4BW f m f f L H -=-=)1(410m f f f Q L H -=-= 则只要我们取m 值接近1时，就能得到窄带滤波效果和高Q 值，使陷波器的性能达到最佳。

源代码：%陷波器的设计%陷波器的传输函数为% B(1/z) (z-exp(j*2*pi*f0))*(z-exp(-j*2*pi*f0))%H(z) = -------- = --------------------------------------------% A(1/z) (z-a*exp(j*2*pi*f0))*(z-a*exp(-j*2*pi*f0))%其中f0为陷波器要滤除信号的频率，a为与陷波器深度相关的参数，a越大，深度越深。

%%已知信号中50Hz工频干扰，信号为x=sin(2*pi*50*n*Ts)+sin(2*pi*125*n*Ts);%要求通过陷波器滤除50Hz干扰信号%参数设置：采样率Ts=0.001s，采样长度：512点clf;clear;%设置初值f0=50;Ts=0.001;fs=1/Ts;NLen=512;n=0:NLen-1;%陷波器的设计apha=-2*cos(2*pi*f0*Ts);beta=0.96;b=[1 apha 1];a=[1 apha*beta beta^2];figure(1);freqz(b,a,NLen,fs);%陷波器特性显示x=sin(2*pi*50*n*Ts)+sin(2*pi*125*n*Ts);%原信号y=dlsim(b,a,x);%陷波器滤波处理%对信号进行频域变换。

xfft=fft(x,NLen);xfft=xfft.*conj(xfft)/NLen;y1=fft(y,NLen);y2=y1.*conj(y1)/NLen;figure(2);%滤除前后的信号对比。

subplot(2,2,1);plot(n,x);grid;xlabel('Time (s)');ylabel('Amplitude');title('Input signal');subplot(2,2,3);plot(n,y);grid;xlabel('Time (s)');ylabel('Amplitude');title('Filter output');subplot(2,2,2);plot(n*fs/NLen,xfft);axis([0 fs/2 min(xfft) max(xfft)]);grid;xlabel('Frequency (Hz)');ylabel('Magnitude (dB)');title('Input signal');subplot(2,2,4);plot(n*fs/NLen,y2);axis([0 fs/2 min(y2) max(y2)]);grid;xlabel('Frequency (Hz)');ylabel('Magnitude (dB)');title('Filter output');100200300400500600-2-112Time (s)A m p l i t u d eInput signal100200300400500600-2-112Time (s)A m p l i t u d eFilter output010020406080100120M a g n i t u d e (d B )010020406080100120M a g n i t u d e (d B )。

陷波器设计陷波器是无限冲击响应(IIR)数字滤波器，该滤波器可以用以下常系数线性差分方程表示：∑∑==---=M i Ni i i i n y b i n x a n y 01)()()( (1)式中： x(n)和y(n)分别为输人和输出信号序列；i a 和i b 为滤波器系数。

对式(1)两边进行z 变换，得到数字滤波器的传递函数为：∏∏∑∑===-=---==N i i M i i N i i iM i ii p z z z z b z a z H 1100)()()( (2)式中：i z 和i p 分别为传递函数的零点和极点。

由传递函数的零点和极点可以大致绘出频率响应图。

在零点处，频率响应出现极小值；在极点处，频率响应出现极大值。

因此可以根据所需频率响应配置零点和极点，然后反向设计带陷数字滤波器。

考虑一种特殊情况，若零点i z 在第1象限单位圆上，极点i p 在单位圆内靠近零点的径向上。

为了防止滤波器系数出现复数，必须在z 平面第4象限对称位置配置相应的共轭零点*i z 、共轭极点*i p 。

这样零点、极点配置的滤波器称为单一频率陷波器，在频率ωo 处出现凹陷。

而把极点设置在零的的径向上距圆点的距离为l-μ处，陷波器的传递函数为：))1()()1(())(()(2121z z z z z z z z z H μμ------= (3) 式(3)中μ越小，极点越靠近单位圆，则频率响应曲线凹陷越深，凹陷的宽度也越窄。

当需要消除窄带干扰而不能对其他频率有衰减时，陷波器是一种去除窄带干扰的理想数字滤波器。

当要对几个频率同时进行带陷滤波时，可以按(2)式把几个单独频率的带陷滤波器(3)式串接在一起。

一个例子：设有一个输入，它由50Hz 信号和100Hz 信号组成。

50Hz 是一个干扰信号，要设计一个50 Hz 的带陷滤波器，采样频率为400Hz 。

4/400/5021ππω=⨯=因此z 平面上的零极点可设置为4/14/1999.0ππj j ep e z ±±== 展开式为70637064)707.0707.0(999.0)4sin 4(cos 999.0999.0707.0707.022224sin 4cos 4/14/1j j j e p j j j e z j j ±=±=±=±=±=±=±±ππππππ＝＝ 它的传递函数为2121221111999.04126.11414.11999.04126.11414.1)7063.07063.0)(7063.07063.0()707.0707.0)(707.0707.0())(())(()(----**+-+-=+-+-=+---+---=----=z z z z z z z z j z j z j z j z p z p z z z z z z H因此分子系数是[1 1.414 1]；分母系数是[1 1.4126 0.999]。

全频喇叭陷波器参数设计
全频喇叭陷波器的参数设计需要考虑以下几个方面：
1. 中心频率：陷波器应该设置在干扰信号的中心频率上。

中心频率的选择需要根据实际情况进行调整，通常可以使用频谱分析仪来确定。

2. 带宽：陷波器的带宽越窄，抑制目标频率的效果越好。

但是带宽设置过窄会影响音频信号的传输，因此需要根据实际情况进行调整。

3. 阻尼系数：阻尼系数决定了陷波器的Q值（品质因数），Q 值越大，带宽越窄，但是对干扰信号的抑制效果也越好。

Q值的选择需要根据实际情况进行调整。

4. 补偿系数：在设计全频喇叭陷波器时，需要考虑到陷波器对音频信号的影响。

为了避免陷波器对音质的影响，需要对输出信号进行补偿处理。

补偿系数的选择需要根据实际情况进行调整。

5. 增益：陷波器的增益可以控制输出信号的音量，需要根据实际情况进行调整。

综上所述，全频喇叭陷波器的参数设计需要综合考虑上述方面，根据实际情况进行调整和优化，才能达到最优的抑制效果和音质表现。

陷波器参数计算引言：陷波器是一种用于抑制特定频率的滤波器，常用于电子通信中的频率选择性网络中。

陷波器的参数计算是设计陷波器的重要步骤之一，本文将介绍陷波器的参数计算方法及其应用。

一、陷波器的基本原理陷波器是一种带阻滤波器，其工作原理是在特定频率处引入一个零点或极点，将该频率信号进行衰减。

陷波器的频率响应呈现出一个深的谷，被抑制频率附近的信号将被滤除。

二、陷波器的参数设计陷波器需要确定以下几个参数：1. 中心频率（f0）：陷波器需要抑制的特定频率。

2. 带宽（BW）：陷波器在中心频率附近的频带范围。

3. 品质因数（Q）：陷波器的频率选择性，Q值越大，陷波器的选择性越高。

4. 陷波器类型：常见的陷波器类型有带阻式和带通式。

三、陷波器参数计算方法1. 中心频率（f0）的确定：中心频率的选择通常基于实际需求，可以根据需要抑制的特定频率来确定。

在无源陷波器中，中心频率可通过电感和电容值的选择来实现。

2. 带宽（BW）的计算：带宽决定了陷波器在中心频率附近的抑制能力。

带宽的计算方法为BW = f0/Q，其中Q为品质因数。

3. 品质因数（Q）的选择：品质因数决定了陷波器的频率选择性能，Q值越大，选择性越高。

品质因数的计算方法为Q = f0/BW。

4. 陷波器类型的选择：根据实际需求，选择合适的陷波器类型。

带阻式陷波器适用于抑制单个频率，而带通式陷波器适用于同时抑制多个频率。

四、陷波器参数计算实例以设计一个带阻式陷波器来抑制50Hz频率为例进行参数计算。

1. 确定中心频率：假设需要抑制的频率为50Hz，则中心频率为50Hz。

2. 计算带宽：假设品质因数Q为10，则带宽为50Hz/10=5Hz。

3. 计算品质因数：假设带宽BW为5Hz，则品质因数为50Hz/5Hz=10。

4. 选择陷波器类型：根据实际需求，选择带阻式陷波器。

五、陷波器的应用陷波器广泛应用于电子通信领域，常见的应用包括：1. 消除干扰信号：在通信系统中，陷波器可以用于滤除特定频率的干扰信号，提高通信质量。

陷波器设计由传递函数的零点和极点可以大致绘出频率响应图。

在零点处，频率响应出 现极小值；在极点处，频率响应出现极大值。

因此可以根据所需频率响应配置零 点和极点，然后反向设计带陷数字滤波器。

考虑一种特殊情况，若零点 Z |在第1 象限单位圆上，极点P i 在单位圆内靠近零点的径向上。

为了防止滤波器系数出 现复数，必须在z 平面第4象限对称位置配置相应的共轭零点Z j 、共轭极点p i < 这样零点、极点配置的滤波器称为单一频率陷波器， 在频率①o 处出现凹陷 而把极点设置在零的的径向上距圆点的距离为1-卩处，陷波器的传递函数为：(Z Z 1)(Z Z 2) (z (1 )zj(z (1 )Z 2)式⑶ 中卩越小，极点越靠近单位圆，贝擞率响应曲线凹陷越深，凹陷的宽 度也越窄。

当需要消除窄带干扰而不能对其他频率有衰减时，陷波器是一种去除 窄带干扰的理想数字滤波器。

当要对几个频率同时进行带陷滤波时，可以按 (2)式把几个单独频率的带陷 滤波器(3)式串接在一起。

一个例子：设有一个输入，它由50Hz 信号和100Hz 信号组成。

50Hz 是一个干扰 信号，要设计一个50 Hz 的带陷滤波器，采样频率为400Hz=12 50/400/4因此z 平面上的零极点可设置为/4P 1 0.999ej /4=0.999(COS ： j sin ：) 0.999(0.707 j0.707) 7064 j7063它的传递函数为陷波器是无限冲击响应 差分方程表示： My(n) aX n式中：x(n)和y(n)分别为输人和输出信号序列；a ：和b 为滤波器系数。

对式(1)两边进行z 变换，得到数字滤波器的传递函数为：Ma i z 1H(z) + b i z 1I 0式中：Z |和P i 分别为传递函数的零点和极点。

i)(IIR)数字滤波器，该滤波器可以用以下常系数线性by( n I) (1)I 1M(z Z |)■N ----------⑵(z P i ) I 1H(z)P 1 展开式为乙0.999e/4e j /4= cos_ 42 2j sin 40.707 j0.707(z Z i)(z Z1)(Z P i)(z p 1) (z 0.707 j0.707)(z 0.707 j 0.707)(z 0.7063 j0.7063)(z 0.7063 j0.7063)2z 1.414z 1 1 1.414z2z 1.4126z 0.999 1 1.4126z 0.999z因此分子系数是[1 1.414 1] 差分方程有y(n) a(2)y( n 1) a(3)y(n y(n) x(n) b(2)x( n 1) ;分母系数是[1 1.4126 0.999]。

陷波器设计陷波器是无限冲击响应(IIR)数字滤波器，该滤波器可以用以下常系数线性差分方程表示：∑∑==---=Mi Ni iii n y bi n x an y 01)()()( (1)式中： x(n)和y(n)分别为输人和输出信号序列；i a 和i b 为滤波器系数。

对式(1)两边进行z 变换，得到数字滤波器的传递函数为：∏∏∑∑===-=---==Ni i Mi iNi iiMi iip z zz zbz az H 1100)()()( (2)式中：i z 和i p 分别为传递函数的零点和极点。

由传递函数的零点和极点可以大致绘出频率响应图。

在零点处，频率响应出现极小值；在极点处，频率响应出现极大值。

因此可以根据所需频率响应配置零点和极点，然后反向设计带陷数字滤波器。

考虑一种特殊情况，若零点i z 在第1象限单位圆上，极点i p 在单位圆内靠近零点的径向上。

为了防止滤波器系数出现复数，必须在z 平面第4象限对称位置配置相应的共轭零点*i z 、共轭极点*i p 。

这样零点、极点配置的滤波器称为单一频率陷波器，在频率ωo 处出现凹陷。

而把极点设置在零的的径向上距圆点的距离为l-μ处，陷波器的传递函数为：))1()()1(())(()(2121z z z z z z z z z H μμ------=(3)式(3)中μ越小，极点越靠近单位圆，则频率响应曲线凹陷越深，凹陷的宽度也越窄。

当需要消除窄带干扰而不能对其他频率有衰减时，陷波器是一种去除窄带干扰的理想数字滤波器。

当要对几个频率同时进行带陷滤波时，可以按(2)式把几个单独频率的带陷滤波器(3)式串接在一起。

一个例子：设有一个输入，它由50Hz 信号和100Hz 信号组成。

50Hz 是一个干扰信号，要设计一个50 Hz 的带陷滤波器，采样频率为400Hz 。

4/400/5021ππω=⨯=因此z 平面上的零极点可设置为4/14/1999.0ππj j ep ez ±±==展开式为70637064)707.0707.0(999.0)4sin4(cos999.0999.0707.0707.022224sin4cos4/14/1j j j ep j jj ez j j ±=±=±=±=±=±=±±ππππππ＝＝它的传递函数为2121221111999.04126.11414.11999.04126.11414.1)7063.07063.0)(7063.07063.0()707.0707.0)(707.0707.0())(())(()(----**+-+-=+-+-=+---+---=----=zzzz z z z z j z j z j z j z p z p z z z z z z H因此分子系数是[1 1.414 1]；分母系数是[1 1.4126 0.999]。

陷波器的主要参数陷波器是一种用于滤除特定频率的信号的电子器件，它在电子通信和无线电频谱管理中起着重要作用。

陷波器的主要参数包括中心频率、带宽、衰减等级和损耗。

本文将对这些主要参数进行详细介绍。

一、中心频率中心频率是陷波器的工作频率，也是其设计的重要参数之一。

它决定了陷波器对特定频率的滤波效果。

中心频率是陷波器设计的关键，需要根据具体应用需求选择合适的频率。

二、带宽带宽是指陷波器在中心频率附近的频段范围。

带宽参数决定了陷波器对信号的滤波效果，带宽越宽，陷波器对周围频率的干扰信号的抑制能力越强。

带宽的选择应根据实际应用场景和需求来确定。

三、衰减等级衰减等级是指陷波器对信号在非中心频率处的衰减程度。

一般来说，衰减等级越高，陷波器对非中心频率的信号抑制效果越好。

衰减等级是陷波器设计的重要指标，可以通过选择合适的滤波结构和参数来实现。

四、损耗损耗是指陷波器在滤波过程中对信号的能量损失。

陷波器的损耗应尽可能小，以确保滤波后信号的准确性和完整性。

损耗主要来自于陷波器的电路结构和材料特性，设计者需要在满足滤波要求的前提下尽量降低损耗。

陷波器的主要参数对于滤波器的性能和应用具有重要影响。

中心频率、带宽、衰减等级和损耗的选择需要根据具体的应用场景和要求来确定。

在实际应用中，设计者需要综合考虑这些参数，选择合适的陷波器来实现所需的滤波效果。

除了上述主要参数，陷波器还有其他一些辅助参数，例如尺寸、重量、工作温度范围等。

这些参数虽然不直接影响陷波器的滤波性能，但在实际应用中也需要考虑。

设计者需要根据具体的应用环境，选择适合的陷波器。

陷波器是一种重要的电子器件，用于滤除特定频率的信号。

中心频率、带宽、衰减等级和损耗是陷波器的主要参数，设计者需要根据实际需求来选择合适的陷波器。

通过合理选择参数和优化设计，陷波器能够在无线通信和电子频谱管理等领域发挥重要作用。