正态分布2
- 格式:ppt
- 大小:3.29 MB
- 文档页数:20
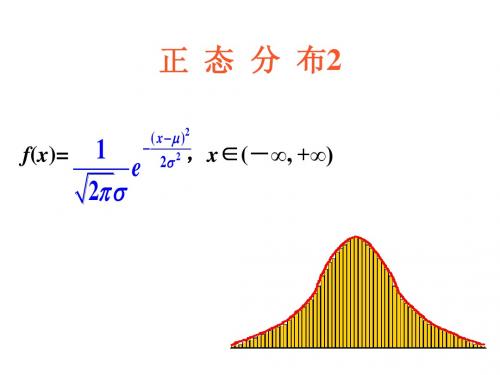
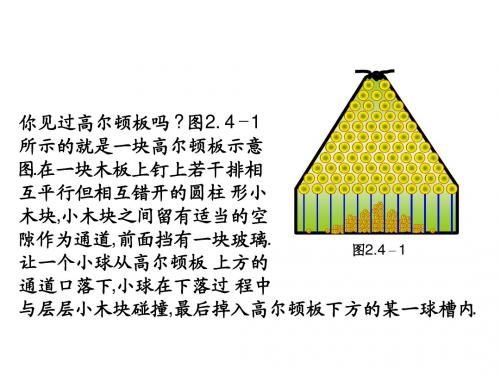


正态分布函数的平方的分布1. 定义正态分布函数的平方的分布,简称正态平方分布,也称为卡方分布。
它是一种概率分布函数,是对正态随机变量的平方进行统计分布研究的结果。
在统计学中,正态平方分布是一种重要的分布,常被应用于假设检验、可信区间估计以及方差分析等领域。
正态平方分布的主要特征是非负、右偏态,其参数由自由度决定。
2. 概率密度函数正态平方分布的概率密度函数如下:f(x;ν)=xν2−1e−x2 2ν2Γ(ν2)其中,x表示随机变量的取值,ν表示自由度,Γ表示伽马函数。
3. 自由度和形状正态平方分布的自由度参数ν的取值大于0,它决定了分布的自由度和形状。
自由度越大,正态平方分布越接近正态分布。
4. 性质(1)期望和方差:正态平方分布的期望和方差如下:期望:E(X)=ν方差:Var(X)=2ν(2)对称性:当自由度ν为偶数时,正态平方分布是对称的;当自由度ν为奇数时,正态平方分布是右偏的。
5. 应用领域和用途正态平方分布在统计学中有着广泛的应用,具体包括以下几个方面:(1)假设检验:正态平方分布可以用于对总体方差进行假设检验。
通过计算正态平方统计量,与给定的显著性水平进行比较,从而判断总体方差是否满足某个假设。
(2)置信区间估计:利用正态平方分布,可以对总体方差进行置信区间估计。
通过计算正态平方统计量的上下临界值,与样本方差进行比较,确定总体方差的置信区间。
(3)方差分析:正态平方分布常用于方差分析中,用于比较两个或多个总体方差是否相等。
通过计算正态平方统计量,与临界值进行比较,从而判断不同总体的方差是否存在显著差异。
(4)回归分析:在回归分析中,正态平方分布可以用于检验回归方程中的误差项方差是否相等。
通过计算正态平方统计量,与指定的显著性水平进行比较,从而判断回归方程中的误差项方差是否存在异方差性。
(5)相关分析:在相关分析中,正态平方分布可以用于检验两个变量之间的方差是否存在差异。
通过计算正态平方统计量,与显著性水平进行比较,从而判断两个变量之间的方差是否相等。


高中数学教案精选-正态分布教学目标:1. 理解正态分布的概念及其性质;2. 学会计算正态分布的概率;3. 能够应用正态分布解决实际问题。
教学重点:1. 正态分布的概念及其性质;2. 正态分布的概率计算。
教学难点:1. 正态分布的概率计算;2. 应用正态分布解决实际问题。
教学准备:1. 投影仪;2. 教学PPT;3. 练习题。
教学过程:一、导入(5分钟)1. 引入正态分布的概念,通过举例让学生感受正态分布的广泛应用;2. 提问:什么是正态分布?它有什么特点?二、新课讲解(15分钟)1. 讲解正态分布的定义及其数学表达式;2. 讲解正态分布的性质,包括对称性、有界性和单峰性;3. 讲解正态分布的概率计算方法,包括累积分布函数和概率密度函数。
三、案例分析(10分钟)1. 通过具体案例,让学生理解正态分布的概率计算方法;2. 让学生尝试解决实际问题,如求解某个正态分布变量的概率。
四、课堂练习(10分钟)1. 给出练习题,让学生独立完成;2. 对学生的答案进行讲解和指导。
五、总结与布置作业(5分钟)1. 对本节课的内容进行总结;2. 布置作业,巩固所学知识。
教学反思:本节课通过导入、新课讲解、案例分析和课堂练习等环节,让学生掌握了正态分布的概念、性质和概率计算方法。
在教学过程中,要注意引导学生主动参与,提高学生的动手能力和解决问题的能力。
结合实际案例,让学生感受数学与生活的紧密联系,激发学生的学习兴趣。
六、正态分布的应用(15分钟)1. 介绍正态分布在日常生活中的应用,如身高、体重、考试成绩等;2. 讲解如何利用正态分布解决实际问题,如估计某个群体的平均身高;3. 让学生尝试解决实际问题,如估计某个班级学生的平均成绩。
七、正态分布的性质与图像(15分钟)1. 讲解正态分布的性质,包括对称性、有界性和单峰性;2. 利用PPT展示正态分布的图像,让学生理解正态分布的形状;3. 讲解如何通过观察正态分布的图像来判断数据的分布情况。
利用正态分布近似计算二项分布的依据和具体做法正态分布近似计算二项分布是一种非常常见和非常有用的方法,它可以帮助我们更好地研究随机事件的概率。
正态分布近似计算二项分布的依据和具体做法是基于多次试验中,其取位置点的概率分布可以用正态分布描述的现象来进行计算的。
具体来说,在运用正态分布近似计算二项分布的时候,我们先要做的是计算出误差度和把它转换为方差。
把误差度转换成方差的过程中,我们用的公式如下:
方差 = 2 * p * q
其中,p和q分别表示成功的概率和失败的概率,都是从二项分布求出的。
得到方差之后,就可以用它来计算出正态分布近似二项分布的均值,公式如下:
均值 = p * n
其中,n表示试验的重复次数,也是从二项分布求出的。
得到均值和方差后,再把这两个量代入正态分布的公式,就可以得到经过正态分布近似的二项分布概率分布。
之后,我们再计算二项分布概率数值,这一步比较简单,最后,我们得到的结果就相当于用正态分布近似计算出来的二项分布了。
总之,正态分布近似计算二项分布的基本原理就是,将二项分布取位置点的概率分布当做一个正态分布来模拟,然后用正态分布的公式去计算,把得到的均值和方差代表二项分布,从而获得近似的结果。
这种做法的优点在于,无论我们的随机事件的概率如何变化,计算的结果都会比较精确,也比较准确。