2018年武汉市中考模拟试题

武汉市黄陂区九年级部分学校数学联考试卷一、选择题（每小题3分，共36分）1．有理数13-的相反数是（ ）A ．3B ．-3C ．13D ．13-2．函数y =x 的取值范围是（ ）A ．x ≥12B ．x ≥12-C ．x ＜12D ．x ＜12-3．不等式组32123x x ⎧⎨+>--≥的解集在数轴上表示正确的是（ ） A. B. C. D. 4. 下列事件为随机事件的为（）A. 两个非负实数的算术平方根相乘结果为非负数B.三角形内角和为180° C. 一元二次方程有实数解D. 对顶角相等5. 若x 1、x2是一元二次方程x 2+ 2x – 3 = 0的两个根，则x 1·x 2的值是（ ） A ．2 B ．-2 C ．3 D ．-36. 法国国家科研中心宣布，欧洲“火星快车”探测器发回的大量数据显示，火星南极地区存在大量的冰，其含量大约为160万立方千米，这一数据用科学记数法（保留三个有效数字）表示为（ ） A ．1.60×118立方千米 B ．1.60×118立方千米 C ．1.6×118立方千米 D ．1.6×118立方千米 7．如图,四边形ABCD 内有一点E ,,AE BE DE BC DC ==== 若0100C ∠=,则BAD ∠的大小是（ ）A. 25oB. 50oC.60oD.80o8. 右图是由八个相同小正方体组合而成的几何体，则其左视图是（ ）9. 如图（1），已知小正方形ABCD 的面积为1，把它的各边延长一倍得到新正方形A 1B 1C 1D 1；把正方形A 1B 1C 1D 1边长按原法延长一倍得到正方形A 2B 2C 2D 2（如图（2））；以此下去···，则正方形A 4B4C 4D 4的边长为( ) A. 4 B. 5 C. 16 D. 2510. 如图，以半圆的一条弦BC （非直径）为对称轴将弧BC 折叠后与直径AB 交于点D ，若32=DB AD ，且10=AB ，则CB 的长为 ( )A ．54B ．34C ． 24D ．411.如图是长春公司2018年2--4月份资金投放总额与利润总额统计示EDCBA AB CD 第9题图（1） A 1B 1C 1D 1A BC D D 2A 2B 2C 2D 1C 1B 1A 1A BC D 第9题图（2）第10题图BB意图, 根据图中的信息判断, 得出下列结论: ①利润总额最高的是4月份;②三个月的月平均利润约为37万元;③4月份的利润率比2月份的利润率高4.4; ④2月至4月利润率的平均增长率为20%. 其中正确的结论是( ).A. ③④B. ①③④C. ①②④D. ①④ 12．如图，在直角梯形ABCD 中，AD∥BC，∠ABC =90°，BE⊥AC 于点E ，CF 平分∠ACB 交BE 于点G ，连结DF 交AC 于点H ，且 DF⊥CF.下列结论：①BF=BG；②△AFH∽△BCG；③CF=DF； ④2HA 2=HD·HF.其中正确结论的个数是 A. 1个 B. 2个C. 3个D. 4个二、填空题（每小题3分，共12分）13．计算tan60°=14. 某班上的一个数学兴趣小组6名学生在本次四月调考中数学成绩如下：92,118,98，101,98,118，这组数据的中位数是 ，平均数是 ，众数是 。

2018武汉中考数学模拟题一一、选择题（共10小题，每小题3分，共30分）1．25的平方根为（）A ．5 B ．±5C ．－5D ．±42．如果分式1x x 无意义，那么x 的取值范围是（）A ．x ≠0B ．x ＝1C ．x ≠1D ．x ＝－1 3．(－a ＋3)2的计算结果是（）A ．－a 2＋9B ．－a 2－6a ＋9C ．a 2－6a ＋9D ．a 2＋6a ＋9 4．在不透明的布袋中，装有大小、形状完全相同的3个黑球、2个红球，从中摸一个球，摸出的是个黑球，这一事件是（）A ．必然事件B ．随机事件C ．确定事件D ．不可能事件5．下列运算结果是a 6的是（）A ．a 3·a3B ．a 3＋a3C ．a 6÷a3D ．(－2a 2)36．将点A(1，－2)绕原点逆时针旋转90°得到点B ，则点B 的坐标为（）A ．(－1，－2)B ．(2，1)C ．(－2，－1)D ．(1，2)7．由6个大小相同的小正方体组合成一个几何体，其俯视图如图所示，其中正方形中的数字表示该位置放置的小正方体的个数，则该几何体的主视图为（）8．在我市开展的“好书伴我成长”读书活动中，学校随机调查了九年级50名学生读书的册数统计数据如下表所示，那么这50名学生读书册数的平均数与中位数分别为（）册数0 1 2 3 4 人数3 1316 171A ．2和3B ．3和3C ．2和2D ．3和2 9．在如图的4×4的方格中，与△ABC 相似的格点三角形（顶点均在格点上）（且不包括△ABC ）的个数有（）A ．23个B ．24个C ．31个D ．32个10．二次函数y ＝mx 2－nx －2过点(1，0)，且函数图象的顶点在第三象限．当m ＋n 为整数时，则mn 的值为（）A ．2321、B ．431、C ．24321、、D ．243、二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：－7－2＝__________ 12．化简：111b b b ＝__________ 13．在－1、0、31、1、2、3中任取两个数，两数相乘结果是无理数的概率是__________14．如图，△ABC 中，AB ＝AC ，∠BAC ＝66°，OD 垂直平分线段AB ，AO 平分∠BAC ，将∠C沿EF （点E 在BC 上，点F 在AC 上）折叠，点C 与点O 恰好重合，则∠OEC ＝___________15．如图，在四边形ABCD 中，AC 与BD 交于点O ，∠DAB 与∠ACB 互补，35OBOD ，AD ＝7，AC ＝6，AB ＝8，则BC ＝___________16．如图，C 是半径为4的半圆上的任意一点，AB 为直径，延长AC 至点P 使CP ＝2CA ．当点C 从B 运动到A 时，动点P 的运动路径长为___________三、解答题（共8题，共72分）17．（本题8分）解方程：x －2(x －1)＝－218．（本题8分）如图，已知点E 、C 在线段BF 上，BE ＝CF ，AB ∥DE ，AC ∥DF ，求证：△ABC≌△DEF19．（本题8分）某校体育组对本校九年级全体同学体育测试情况进行调查，他们随机抽查部分同学体育测试成绩（由高到低分四个等级），根据调查的数据绘制成如下的条形统计图和扇形统计图请根据以上不完整的统计图提供的信息，解答下列问题：(1) 该课题研究小组共抽查了__________名同学的体育测试成绩，扇形统计图中B 级所占的圆心角是__________ (2) 补全条形统计图(3) 若该校九年级共有200名同学，请估计该校九年级同学体育测试达标（测试成绩C 级以上，含C 级）均有名20．（本题8分）某校安排6名教师和300名学生春游，准备租用45座大客车和30座的小客车．若租用1辆大客车和2辆小客车共需租金960元；若租用2辆大客车和1辆小客车共需租金1080元(1) 求1辆大客车和1辆小客车的租金各为多少元？(2) 若总共租用8辆客车，总费用不超过3080元，问有几种租车方案，最省钱的方案是哪种？21．（本题8分）如图，BC 为⊙O 的直径，点A 为⊙O 上一点，点E 为△ABC 的内心，OE ⊥EC (1) 若BC ＝10，求DE 的长(2) 求sin ∠EBO 的值22．（本题10分）如图，直线y ＝2x 与函数xk y（x ＞0）的图象交于第一象限的点A ，且A 点的横坐标为1，过点A 作AB ⊥x 轴于点B ，C 为射线BA 上一点，作CE ⊥AB 交双曲线于点E ，延长OC 交AE 于点F (1) 则k ＝__________(2) 作EM ∥y 轴交直线OA 于点M ，交OC 于点G ①求证：AF ＝FE②比较MG 与EG 的大小，并证明你的结论23．（本题10分）如图，在△ABC 与△AFE 中，AC ＝2AB ，AF ＝2AE ，∠CAB ＝∠FAE ＝α(1) 求证：∠ACF ＝∠ABE(2) 若点G 在线段EF 上，点D 在线段BC 上，且31CBCD EF GF ，α＝90°，EB ＝1，求线段GD的长(3) 将(2)中改为120°，其它条件不变，请直接写出CFGD 的值24．（本题12分）在平面直角坐标系中，抛物线C 1：y ＝ax 2＋bx －1的最高点为点D (－1，0)，将C 1左移1个单位，上移1个单位得到抛物线C 2，点P 为C 2的顶点(1) 求抛物线C 1的解析式(2) 若过点D 的直线l 与抛物线C 2只有一个交点，求直线l 的解析式(3) 直线y ＝x ＋c 与抛物线C 2交于D 、B 两点，交y 轴于点A ，连接AP ，过点B 作BC ⊥AP 于点C ，点Q 为C 2上PB 之间的一个动点，连接PQ 交BC 于点E ，连接BQ 并延长交AC 于点F ，试说明：FC ·(AC ＋EC)为定值2018武汉中考数学模拟题二一、选择题（共10小题，每小题3分，共30分）1．64的算术平方根是（）A ．8B ．－8C ．4D ．－42．要使分式15x 有意义，则x 的取值范围是（）A ．x ≠1B ．x ＞1C ．x ＜1D ．x ≠－13．下列计算结果为x 8的是（）A ．x 9－x B ．x 2·x4C ．x 2＋x6D ．(x 2)44．有两个事件，事件A ：投一次骰子，向上的一面是3；事件B ：篮球队员在罚球线上投篮一次，投中，则（）A ．只有事件A 是随机事件B ．只有事件B 是随机事件C ．事件A 和B 都是随机事件D ．事件A 和B 都不是随机事件5．计算(a －3)2的结果是（）A ．a 2－4 B ．a 2－2＋4 C ．a 2－4a ＋4D ．a 2＋46．如图，将△AOB 绕点O 逆时针旋转90°，得到△A ′OB ′．若点A 的坐标为(a ，b)，则点A ′的坐标为（）A ．(a ，b)B ．(－a ，b)C ．(b ，－a)D ．(－b ，a)7．如图是由一些小正方体组合而成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，则这个几何体主视图是（）8．某小组5名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是（）劳动时间（小时）3 3.54 4.5 人数1121A ．中位数是4，平均数是 3.75B ．众数是4，平均数是 3.75C ．中位数是4，平均数是3.8 D ．众数是2，平均数是 3.89．把所有正奇数从小到大排列，并按如下规律分组：(1) (3，5，7)、(9，11，13，15，17)，(19，21，23，25，27，29，31)，……，现有等式A m ＝(i ，j)表示正奇数m 是第i 组第j 个数（从左往右数），如A 7＝(2，3)，则A 89＝（）A ．(6，7)B ．(7，8)C ．(7，9)D ．(6，9)10．二次函数y ＝2x 2－2x ＋m （0＜m ＜21），如果当x ＝a 时，y ＜0，那么当x ＝a －1时，函数值y 的取值范围为（）A ．y ＜0B ．0＜y ＜mC ．m ＜y ＜m ＋4D ．y ＞m二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：(－3)＋8＝___________12．计算：111a a a ＝___________ 13．不透明的袋子中有6个除了颜色不同其他都一样的球，其中有3个黑球，2个白球，1个红球．拿出两个球，颜色相同的概率是___________14．如图，E 是矩形ABCD 的对角线的交点，点F 在边AE 上，且DF ＝DC ．若∠ADF ＝25°，则∠BEC ＝__________ 15．如图，从一张腰为60 cm ，顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形OCD ，用次剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为__________16．已知OM ⊥ON ，斜边长为4的等腰直角△ABC 的斜边AC 在射线ON 上，顶点C 与O 重合．若点A 沿NO 方向向O 运动，△ABC 的顶点C 随之沿OM 方向运动，点A 移动到点O 为止，则直角顶点B 运动的路径长是__________三、解答题（共8题，共72分）17．（本题8分）解方程：3－(5－2x)＝x ＋218．（本题8分）已知：如图，点B 、F 、C 、E 在一条直线上，BF ＝CE ，AC ＝DF ，且AC ∥DF ，求证：∠B ＝∠E19．（本题8分）某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费，为更好地决策，自来水公司的随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图，（每组数据包括在右端点但不包括左端点），请你根据统计图解答下列问题：(1) 此次抽样调查的样本容量是___________(2) 补全频数分布直方图，求扇形图中“15吨～20吨”部分的圆心角的度数(3) 如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？20．（本题8分）荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）(1) 求桂味和糯米糍的售价分别是每千克多少元(2) 如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低21．（本题8分）如图，直径AE 平分弦CD ，交CD 于点G ，EF ∥CD ，交AD 的延长线于F ，AP ⊥AC 交CD 的延长线于点P(1) 求证：EF 是⊙O 的切线(2) 若AC ＝2，PD ＝21CD ，求tan ∠P 的值22．（本题10分）已知，直线l 1：y ＝－x ＋n 过点A(－1，3)，双曲线C ：xm y（x ＞0），过点B(1，2)，动直线l 2：y ＝kx －2k ＋2（k ＜0）恒过定点F(1) 求直线l 1，双曲线C 的解析式，定点F 的坐标(2) 在双曲线C 上取一点P(x ，y)，过P 作x 轴的平行线交直线l 1于M ，连接PF ，求证：PF＝PM (3) 若动直线l 2与双曲线C 交于P 1、P 2两点，连接OF 交直线l 1于点E ，连接P 1E 、P 2E ，求证：EF平分∠P 1EP 223．（本题10分）已知△ABC 中，D 为AB 边上任意一点，DF ∥AC 交BC 于F ，AE ∥BC ，∠CDE＝∠ABC ＝∠ACB ＝α(1) 如图1，当α＝60°时，求证：△DCE 是等边三角形(2) 如图2，当α＝45°时，求证：①2DECD ；②CE ⊥DE(3) 如图3，当α为任意锐角时，请直接写出线段CE 与DE 的数量关系（用α表示）24．（本题12分）在平面直角坐标系xOy 中，抛物线c 1：y ＝ax 2－4a ＋4（a ＜0）经过第一象限内的定点P (1) 直接写出点P 的坐标(2) 若a ＝－1，如图1，点M 的坐标为(2，0)是x 轴上的点，N 为抛物线c 1上的点，Q 为线段MN 的中点，设点N 在抛物线c 1上运动时，Q 的运动轨迹为抛物线c 2，求抛物线c 2的解析式(3) 直线y ＝2x ＋b 与抛物线c 1相交于A 、B 两点，如图2，直线PA 、PB 与x 轴分别交于D 、C 两点，当PD ＝PC 时，求a 的值2018武汉中考数学模拟题三一、选择题（共10小题，每小题3分，共30分）1．4的值为（）A ．±2B ．2C ．－2D ．22．要使分式31x 有意义，则x 的取值应满足（）A ．x ≥3B ．x ＜3C ．x ≠－3D ．x ≠3 3．下列计算结果为x 6的是（）A ．x ·x6B ．(x 2)3C ．x 7－xD ．x 12÷x24．袋中装有4个红球和2个黄球，这些球的形状、大小、质地完全相同．在看不到球的条件下，随机地从袋子中摸出三个球，下列事件是不可能事件的是（）A ．摸出的三个球中至少有一个红球B ．摸出的三个球中有两个球是黄球C ．摸出的三个球都是红球D ．摸出的三个球都是黄球5．计算(a －1)2正确的是（）A ．a 2－1B ．a 2－2a ＋1 C ．a 2－2a －1D ．a 2－a ＋1 6．在平面直角坐标系中，将点A(x ，y)向左平移5个单位长度，再向上平移3个单位长度后与点B(－3，2)重合，则点A 的坐标为（）A ．(3，1)B ．(2，－1)C ．(4，1)D ．(3，2)7．如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的左视图是（）8．为调查某班学生每天使用零花钱的情况，童老师随机调查了30名同学，结果如下表：每天使用零花钱（单位：元）5 10 15 20 25 人数258 96则这30名同学每天使用的零花钱的众数和中位数分别是（）A ．20、15B ．20、17.5C ．20、20D ．15、15 9．正方形A 1B 1C 1O 、A 2B 2C 2C 1、A 3B 3C 3C 2、……按如图的方式放置，点A 1、A 2、A 3……和点C 1、C 2、C 3……分别在直线y ＝x ＋1和x 轴上，则点B 6的坐标是（）A ．(31，16)B ．(63，32)C ．(15，8)D ．(31，32)10．已知关于x 的二次函数y ＝x 2－2x －2，当a ≤x ≤a ＋2时，函数有最大值1，则a 的值为（）A ．－1或1B ．1或－3C ．－1或3D ．3或－3二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：2－(－4)＝___________ 12．计算：1212x x x ＝___________13．学校为了了解九年级学生“一分钟跳绳次数”的情况，随机选取了4名女生和2名男生，则从这6名学生中选取2名同时跳绳，恰好选中一男一女的概率是___________14．如图，将矩形ABCD 沿BD 翻折，点C 落在P 点处，连接AP ．若∠ABP ＝26°，则∠APB ＝___________15．已知平行四边形内有一个内角为60°，且60°的两边长分别为3、4．若有一个圆与这个平行四边形的三边相切，则这个圆的半径为___________16．如图，已知线段AB＝6，C、D是AB上两点，且AC＝DB＝1，P是线段CD上一动点，在AB 同侧分别作等边△APE和△PBF，G为线段EF的中点，点P由点C移动到点D时，G点移动的路径长度为___________三、解答题（共8题，共72分）17．（本题8分）解方程：2x＋8＝6x－3(x－1)18．（本题8分）已知：如图，BD⊥AC于点D，CE⊥AB于点E，AD＝AE，求证：BE＝CD19．（本题8分）某市三景区是人们节假日游玩的热点景区，某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查．调查分四个类别：A、游三个景区；B、游两个景区；C、游一个景区；D、不到这三个景区游玩．现根据调查结果绘制了不完整的条形统计图和扇形统计图，请结合图中信息解答下列问题：(1) 九(1)班共有学生______人，在扇形统计图中，表示“B类别”的扇形的圆心角的度数为______(2) 请将条形统计图补充完整(3) 若该校九年级有1000名学生，求计划“五一”小长假随父母到该景区游玩的学生多少名？20．（本题8分）运输360吨化肥，装载了6辆大卡车和3辆小汽车；运输440吨化肥，装载了8辆大卡车和2辆小汽车(1) 每辆大卡车与每辆小汽车平均各装多少吨化肥？(2) 现在用大卡车和小汽车一共10辆去装化肥，要求运输总量不低于300吨，则最少需要几辆大卡车？21．（本题8分）如图，⊙O 是△ABC 的外接圆，弧AB ＝弧AC ，AP 是⊙O 的切线，交BO 的延长线于点P(1) 求证：AP ∥BC (2) 若tan ∠P ＝43，求tan ∠PAC 的值22．（本题10分）如图，一次函数y ＝kx ＋b （k ≠0）的图象与反比例函数xm y（m ≠0）的图象交于A(－3，1)、B(1，n)两点(1) 求反比例函数和一次函数的解析式(2) 设直线AB 与y 轴交于点C ，若点P 在x 轴上，使BP ＝AC ，请直接写出点P 的坐标(3) 点H 为反比例函数第二象限内的一点，过点H 作y 轴的平行线交直线AB 于点G ．若HG ＝2，求此时H 的坐标23．（本题10分）如图，射线BD 是∠MBN 的平分线，点A 、C 分别是角的两边BM 、BN 上两点，且AB ＝BC ，E 是线段BC 上一点，线段EC 的垂直平分线交射线BD 于点F ，连接AE 交BD 于点G ，连接AF 、EF 、FC (1) 求证：AF ＝EF (2) 求证：△AGF ∽△BAF(3) 若点P 是线段AG 上一点，连接BP ．若∠PBG ＝21∠BAF ，AB ＝3，AF ＝2，求GPEG24．（本题12分）如图，抛物线y ＝ax 2－(2a ＋1)x ＋b 的图象经过(2，－1)和(－2，7)且与直线y＝kx －2k －3相交于点P(m ，2m －7)(1) 求抛物线的解析式(2) 求直线y ＝kx －2k －3与抛物线y ＝ax 2－(2a ＋1)x ＋b 的对称轴的交点Q 的坐标(3) 在y 轴上是否存在点T ，使△PQT 的一边中线等于该边的一半？若存在，求出点T 的坐标；若不存在，请说明理由一、选择题（共10小题，每小题3分，共30分）题号12345678910答案B C B D B B A B D A第10题选A (1)0122＜，即＜a a a 当1222a ay a x 最大时，舍去），(31a a （2）122aa a，即12)2(2)2(22222a a a ay a a x 最大时，或无解。

湖北省武汉市东西湖区2018年中考二模语文试卷一、（共12分，每小题3分）1．下列各组词语中加点字的读音或书写有误的一组是（）A．嗔视桑梓（zǐ）吹毛求疵（cī）汗流浃背B．匮乏羸弱（yíng）浪敛波平（liǎn）眼花嘹乱C．耷拉慰藉（jiè）屏气凝神（bǐng）钟灵毓秀D．磕绊窒息（zhì）入不敷出（fū）栩栩如生2．依次填入下面横线处的词语，恰当的一组是（）家风，也就是门风，顾名思义，家庭或家族世代相传的风气。

中国讲族系、宗亲，往大了看，庄园有良田万顷，世家有书香传承；往小了看，仅是我们生活的一个小单元、小圈子。

有的家族，支系庞大；有的家族，谱系简单。

家庭，不论大小，都有闪光点，它们不一定似烟花般，不一定如星辰般，只要它们曾经指引我们、感动我们，让我们觉醒过、顿悟过，这就形成了良好的家风。

A．开枝散叶零零散散流光溢彩闪烁夺目B．开枝散叶零零散散闪烁夺目流光溢彩C．零零散散开枝散叶闪烁夺目流光溢彩D．零零散散开枝散叶流光溢彩闪烁夺目3．下列各句中有语病的一项是（）A．由于人们重视信念、理想、精神层面的追求和向往，才出现了众多伟大人物，他们成为各个时代的旗帜，推动社会不断进步。

B．我们重温经典的诗词文本，不是因为它们行将消失、即将毁灭，也不是因为我们忧思古人、恋旧复古，而是因为它们记述着我们民族所特有的精神追求、人文精神和智慧力量。

C．网络文学领域实绩与泡沫共存，竞争与机遇同在，同时有很大的提升空间，网络文学的健康发展尤其需要良好的“生态系统”。

D．“牛蛙简历”与“神童证书”照射出的是家长深深的焦虑，以及不太理会学生成长规律和学习规律的。

4．下列各句标点符号使用不规范的一项是（）A．“唯有牡丹真国色，花开时节动京城。

”近日，圆明园的百种牡丹迎来盛花期。

此外，园内的丁香、桃花、海棠、二月兰等也相继开放，吸引大批游客前来观赏。

B．爱人者，人恒爱之；敬人者，人恒敬之。

只要人与人之间能以仁爱之心相待，又有共同的美好志向，实现和睦相处并不难。

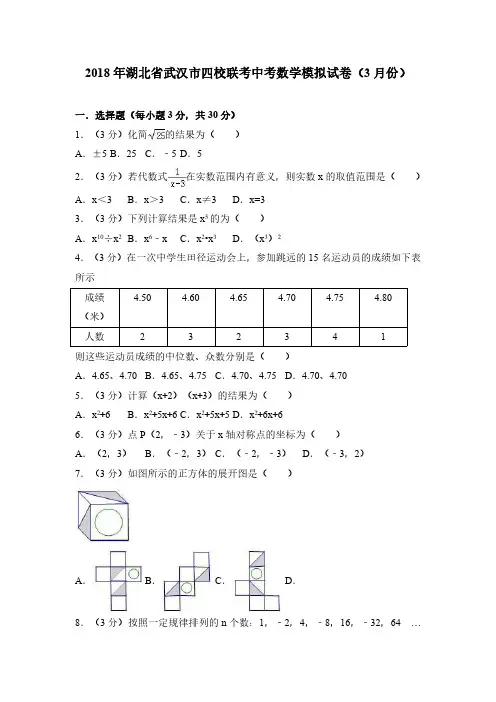
2018年湖北省武汉市四校联考中考数学模拟试卷（3月份）一．选择题（每小题3分，共30分）1．（3分）化简的结果为（）A ．±5B ．25C ．﹣5D ．52．（3分）若代数式在实数范围内有意义，则实数x 的取值范围是（）A ．x ＜3B ．x ＞3C ．x ≠3D ．x=33．（3分）下列计算结果是x 5的为（）A ．x 10÷x 2B ．x 6﹣xC ．x 2•x 3D ．（x 3）24．（3分）在一次中学生田径运动会上，参加跳远的15名运动员的成绩如下表所示成绩（米） 4.504.604.654.704.754.80人数232341则这些运动员成绩的中位数、众数分别是（）A ．4.65、4.70B ．4.65、4.75C ．4.70、4.75D ．4.70、4.705．（3分）计算（x +2）（x +3）的结果为（）A ．x 2+6B ．x 2+5x +6C ．x 2+5x +5D ．x 2+6x +66．（3分）点P （2，﹣3）关于x 轴对称点的坐标为（）A ．（2，3）B ．（﹣2，3）C ．（﹣2，﹣3）D ．（﹣3，2）7．（3分）如图所示的正方体的展开图是（）A ．B ．C ．D ．8．（3分）按照一定规律排列的n 个数：1，﹣2，4，﹣8，16，﹣32，64…若最后两个数的差为﹣1536，则n为（）A．9B．10C．11D．129．（3分）已知一个三角形的三边长分别是6、7、8，则其内切圆直径为（）A．B．C．D．210．（3分）已知抛物线y1=（x﹣x1）（x﹣x2）交x轴于A（x1，0）B（x2，0）两点，且点A在点B的左边，直线y2=2x+t经过点A．若函数y=y1+y2的图象与x轴只有一个公共点时，则线段AB的长为（）A．4B．8C．16D．无法确定二．填空题（每小题3分，共18分）11．（3分）计算﹣2+3×4的结果为12．（3分）计算：=．13．（3分）将对边平行的纸带折叠成如图所示，已知∠1=52°，则∠α=．14．（3分）一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同，随机摸出两个小球，则摸出两个颜色不同小球的概率是．15．（3分）如图，等边△ABC的边长为8，D、E两点分别从顶点B、C出发，沿边BC、CA以1个单位/s、2个单位/s的速度向顶点C、A运动，DE的垂直平分线交BC边于F点，若某时刻tan∠CDE=时，则线段CF的长度为．16．（3分）在平面直角坐标系中，A（4，0），直线l：y=6与y轴交于点B，点P是直线l上点B右侧的动点，以AP为边在AP右侧作等腰Rt△APQ，∠APQ=90°，当点P的横坐标满足0≤x≤8，则点Q的运动路径长为．三、解答题（共8小题，满分72分）17．（8分）解方程：7x﹣5=3x﹣1．18．（8分）如图，点C，F，E，B在一条直线上，∠CFD=∠BEA，CE=BF，DF=AE，写出CD与AB之间的关系，并证明你的结论．19．（8分）某公司为了掌握职工的工作成绩，随机抽取了部分职工的平时成绩（得分为整数，满分为160分）分为5组，第一组85～100；第二组100～115；第三组115～130；第四组130～145；第五组145～160，统计后得到如图所示的频数分布直方图（每组含最小值不含最大值）和扇形统计图，观察图形的信息，回答下列问题：（1）写出本次调查共抽取的职工数为（2）若将得分转化为等级，规定：得分低于100分评为“D”，100～130分评为“C”，130～145分评为“B”，145～160分评为“A”，求该公司1500名工作人员中，成绩评为“B”的人员大约有多少名？20．（8分）某校团委为了教育学生，开展了以感恩为主题的有奖征文活动，并为获奖的同学颁发奖品．小红与小明去文化商店购买甲、乙两种笔记本作为奖品，若买甲种笔记本20个，乙种笔记本10个，共用110元；且买甲种笔记本30个比买乙种笔记本20个少花10元．（1）求甲、乙两种笔记本的单价各是多少元？（2）若本次购进甲种笔记本的数量比乙种笔记本的数量的2倍还少10个，且购进两种笔记本的总数量不少于80本，总金额不超过320元．请你设计出本次购进甲、乙两种笔记本的所有方案．21．（8分）如图，⊙O为正方形ABCD的外接圆，E为弧BC上一点，AF⊥DE于F，连OF、OD．（1）求证：AF=EF；（2）若=，求sin∠DOF的值．22．（10分）如图，在△ABC中，AC=BC，AB⊥x轴于A，反比例函数y=（x ＞0）的图象经过点C，交AB于点D，已知AB=4，BC=．（1）若OA=4，求k的值．（2）连接OC，若AD=AC，求CO的长．23．（10分）如图，在四边形ABCD中，AB∥CD，∠ADC=90°，DE⊥BC于E，连AE，FE⊥AE交CD于点F．（1）求证：△AED∽△FEC；（2）若AB=2，求DF的值；（3）若AD=CD，=2，则=．24．（12分）如图，二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点，与y 轴交于点C，OB=OC，点D在函数图象上，CD∥x轴且CD=2，直线l是抛物线的对称轴，E是抛物线的顶点．（1）求b、c的值；（2）如图1，连BE，线段OC上的点F关于直线l的对称点F’恰好在线段BE 上，求点F的坐标；（3）如图2，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N．试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？若存在，求出点Q的坐标；若不存在，说明理由．2018年湖北省武汉市四校联考中考数学模拟试卷（3月份）参考答案与试题解析一．选择题（每小题3分，共30分）1．【解答】解：∵表示25的算术平方根，∴=5．故选：D．2．【解答】解：依题意得：x﹣3≠0，解得x≠3，故选：C．3．【解答】解：A、x10÷x2=x8，不符合题意；B、x6﹣x不能进一步计算，不符合题意；C、x2•x3=x5，符合题意；D、（x3）2=x6，不符合题意；故选：C．4．【解答】解：这些运动员成绩的中位数、众数分别是4.70，4.75．故选：C．5．【解答】解：（x+2）（x+3）=x2+3x+2x+6=x2+5x+6，故选：B．6．【解答】解：点P（2，﹣3）关于x轴对称点的坐标为（2，3），故选A．7．【解答】解：根据带有各种符号的面的特点及位置，可得如图所示的正方体的展开图是．故选：A．8．【解答】解：观察数列，可知：第n个数为（﹣2）n﹣1．设倒数第二个数为x，则最后一个数为﹣2x，根据题意得：x﹣（﹣2x）=﹣1536，解得：x=﹣512，∴﹣2x=1024，∴（﹣2）n﹣1=1024，∴n=11．故选：C．9．【解答】解：AB=7，BC=6，AC=8，内切圆的半径为r，切点为G、E、F，作AD⊥BC于D，设BD=x，则CD=6﹣x，在Rt△ABD中，AD2=AB2﹣BD2，在Rt△ACD中，AD2=AC2﹣CD2，∴AB2﹣BD2=AC2﹣CD2，即72﹣x2=82﹣（6﹣x）2，解得，x=，则AD==，×AD×BC=×AB×r+×AC×r+×CB×r，解得，r=，∴其内切圆直径为2，故选：D．10．【解答】解：∵线y2=2x+t经过点A（x1，0），∴2x1+t=0∴x1=﹣，A（﹣，0）∵若函数y=y1+y2的图象与x轴只有一个公共点，∴这个公共点就是点A，∴可以假设y=（x+）2=x2+tx+，∴y1=y﹣y2=x2+（t﹣2）x+﹣t．∴AB=====8．故选：B．二．填空题（每小题3分，共18分）11．【解答】解：﹣2+3×4=﹣2+12=10，故答案为：10．12．【解答】解：==x+2．故答案为x+2．13．【解答】解：∵对边平行，∴∠2=∠α，由折叠可得，∠2=∠3，∴∠α=∠3，又∵∠1=∠4=52°，∴∠α=（180°﹣52°）=64°，故答案为：62°．14．【解答】解：画树状图如下：由树状图可知，共有20种等可能结果，其中取出的小球颜色不同的有12种结果，∴两次取出的小球颜色不同的概率为=，故答案为：．15．【解答】解：作EH⊥BC于H，设线段DE的垂直平分线交DE于G．∵△ABC是等边三角形，∴∠C=60°，在Rt△EHC中，EC=2t，∴CH=t，EH=2t，在Rt△DEH中，∵tan∠CDE==，∴DH=4t，∵BD=t，BC=8，∴t+4t+t=8，∴t=，∴DH=，EH=，CH=，∵GF垂直平分线段DE，∴DF=EF，设DF=EF=x，在Rt△EFH中，∵EF2=EH2+FH2，∴x2=（）2+（﹣x）2，解得x=，∴CF=﹣+=2．故答案为2．16．【解答】解：如图，过点P作PE⊥OA，垂足为E，过点Q作QF⊥BP，垂足为F，∵BP∥OA，PE⊥OA，∴∠EPF=∠PEO=90°．∵∠APQ=90°，∴∠EPA=∠FPQ=90°﹣∠APF．在△PEA和△PFQ中，∵，∴△PEA≌△PFQ（AAS），∴PE=PF，EA=QF，若点P的坐标为（a，6），则PF=PE=6，QF=AE=|4﹣a|．∴点Q的坐标为（a+6，10﹣a）．∵无论a为何值，点Q的坐标（a+6，10﹣a）都满足一次函数解析式y=﹣x+16，∴点Q始终在直线y=﹣x+16上运动．当点P的横坐标满足0≤x≤8时，点Q的横坐标满足6≤x≤14，纵坐标满足2≤y≤10，则Q的运动路径长为=8，故答案为：8．三、解答题（共8小题，满分72分）17．【解答】解：（1）移项得7x﹣3x=5﹣1，合并同类项得4x=4，系数化为1得x=1．18．【解答】解：CD∥AB，CD=AB，理由是：∵CE=BF，∴CE﹣EF=BF﹣EF，∴CF=BE，在△AEB和△CFD中，，∴△AEB≌△CFD（SAS），∴CD=AB，∠C=∠B，∴CD∥AB．19．【解答】解：（1）本次调查共抽取的职工数为20÷40%=50（人），故答案为：50；（2）1500×=420（人），答：成绩评为“B”的人员大约有420名．20．【解答】解：（1）设甲种笔记本的单价是x元，乙种笔记本的单价是y元．（1分）根据题意可得（3分）解这个方程组得（4分）答：甲种笔记本的单价是3元，乙种笔记本的单价是5元．（5分）（2）设本次购买乙种笔记本m个，则甲种笔记本（2m﹣10）个．（6分）根据题意可得m+（2m﹣10）≥80，解这个不等式得m≥30，3（2m﹣10）+5m≤320（8分）解这个不等式得m≤31．（9分）因为m为正整数，所以m的值为：30或31故本次购进甲笔记本50个、乙笔记本30个；或购进甲笔记本52个、乙笔记本31个．（10分）21．【解答】证明：（1）如图，过B作BG⊥AF于G，连接BE、OB，∵AF⊥DE，∴∠AGB=∠AFD=90°，∴∠BAF+∠ABG=90°，∵四边形ABCD是正方形，∴BD为⊙O的直径，AD=AB，∠BAD=90°，∴∠DAF+∠BAF=90°，∠BED=90°，∴∠ABG=∠DAF，∴△ABG≌△DAF，∴BG=AF，∵∠BED=∠BGF=∠AFE=90°，∴四边形GBEF是矩形，∴EF=BG，∴AF=EF；（2）作OH⊥BE于H，连接AO，GO．∵OH⊥BE，∴BH=HE，∴OH垂直平分线段BE，∵四边形GBEF是矩形，∴BE=GF，BE∥GF，∴OH垂直平分线段FG，∴OG=OF，∵∠AOD=∠AFD=90°，∴A、D、F、O四点共圆，∴∠DOF=∠DAF，∠OFG=∠ADO=45°，∴△FOG是等腰直角三角形，∴FG=OF，∵EF=BG=AF=2OF，∴AF=2FG，AG=FG=DF，设DF=a，则AF=2a，AD=a，∴sin∠DOF=sin∠DAF==．22．【解答】解：（1）作CE⊥AB，垂足为E，∵AC=BC，AB=4，∴AE=BE=2．在Rt△BCE中，BC=，BE=2，∴CE=，∵OA=4，∴C点的坐标为：（，2），∵点C在y=（x＞0）的图象上，∴k=11；（2）设A点的坐标为（m，0），∵BD=BC=，∴AD=，∴D，C两点的坐标分别为：（m，），（m+，2）．∵点C，D都在y=（x＞0）的图象上，∴m=2（m+），∴m=6，∴C点的坐标为：（，2），作CF⊥x轴，垂足为F，∴OF=，CF=2，在Rt△OFC中，OC2=OF2+CF2，∴OC==．23．【解答】解：（1）∵DE⊥BC，EF⊥AE，∴∠BED=∠CED=90°，∵∠2+∠3=90°，∠2+∠CEF=90°，∴∠CEF=∠3，∵∠AEF=∠ADF=90°∴∠6+∠4=180°，∵∠5+∠6=180°，∴∠5=∠4，∴△ADE∽△FEC．（2）∵∠1+∠3=90°，∠2+∠3=90°，∴∠1=∠2，∵AB∥CD，∠ADC=90°，∴∠BAD+∠ADC=180°，∴∠BAD=90°，∵∠BED+∠BAD=180°，∴四边形ABCD四点共圆，∵∠AEF+∠ADF=180°，∴四边形AEFD四点共圆，∴A、B、E、F、D五点共圆，∵∠1=∠2，∴DF=AB=2．（3）作CN⊥AB交AB的延长线于N，过点E作EG⊥AN垂足为G交CD于H，延长DE交CN于M．∵==2，AB=FD，∴EG=2EH，∵GB∥CH，∴△EGB∽△EHC，∴==2，设EC=a，AB=x，CD=y，则EB=2a，∵∠NCD=∠ADC=∠DAN=90°，∴四边形ADCN是矩形，∵AD=DC∴四边形ADCN是正方形，∴AN=CN=CD=y，NB=y﹣x，∵∠NCB+∠CMD=90°，∠CMD+∠MDC=90°∴∠NCB=∠MDC，∵CN=CD，∴△CNB≌△DCM，∴CM=BN=y﹣x，DM=BC=3a，∵∠MCD=∠MEC，∠CME=∠CMD，∴△MCE∽△MDC，∴=，∴=，∴y2﹣xy=3a2①∵CM2+CD2=MD2，∴（y﹣x）2+y2=9a2②由①②消去a得x2+xy﹣y2=0∴x=y，（或x=y舍弃）∴=，∴=．故答案为：．24．【解答】解：（1）∵CD∥x轴，CD=2，∴抛物线对称轴为x=1．∴﹣=1，b=2．∵OB=OC，C（0，c），∴B点的坐标为（﹣c，0），∴0=﹣c2+2c+c，解得c=3或c=0（舍去），∴c=3；（2）设点F的坐标为（0，m）．∵对称轴为直线x=1，∴点F关于直线l的对称点F的坐标为（2，m）．由（1）可知抛物线解析式为y=﹣x2+2x+3=﹣（x﹣1）2+4，∴E（1，4），∵直线BE经过点B（3，0），E（1，4），∴利用待定系数法可得直线BE的表达式为y=﹣2x+6．∵点F在BE上，∴m=﹣2×2+6=2，即点F的坐标为（0，2）；（3）存在点Q满足题意．设点P坐标为（n，0），则PA=n+1，PB=PM=3﹣n，PN=﹣n2+2n+3．作QR⊥PN，垂足为R，=S△APM，∵S△PQN∴（n+1）（3﹣n）=（﹣n2+2n+3）•QR，∴QR=1．①点Q在直线PN的左侧时，Q点的坐标为（n﹣1，﹣n2+4n），R点的坐标为（n，﹣n2+4n），N点的坐标为（n，﹣n2+2n+3）．∴在Rt△QRN中，NQ2=1+（2n﹣3）2，∴n=时，NQ取最小值1．此时Q点的坐标为（，）；②点Q在直线PN的右侧时，Q点的坐标为（n+1，n2﹣4）．同理，NQ2=1+（2n﹣1）2，∴n=时，NQ取最小值1．此时Q点的坐标为（，）．综上可知存在满足题意的点Q，其坐标为（，）或（，）．。

湖北省武汉市华师一附中2017-2018学年九年级6月中考数学模拟试卷学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 如果水位下降4m，记作﹣4m，那么水位上升5m，记作（）A．1m B．9m C．5m D．﹣52. 花粉大小因种而不同，变化很大．最小的花粉是紫草科的勿忘草，直径约为0.0000025米，用科学记数法表示0.0000025为（）A．0.25×10﹣5B．2. 5×10﹣6C．25×10﹣7D．2.5×1063. 同时使分式有意义，又使分式无意义的x的取值范围是（）A．x≠﹣4，且x≠B．x=﹣4，或x=2 C．x=﹣4 D．x=2﹣24. 下列事件中，属于必然事件的是（）A．随时打开电视机，正在播新闻B．优秀射击运动员射击一次，命中靶心C．抛掷一枚质地均匀的骰子，出现4点朝上D．长度分别是3cm，5cm，6cm的三根木条首尾相接，组成一个三角形5. 如果自然数a是一个完全平方数，那么与a之差最小且比a大的一个完全平方数是（）A．a+1 B．a2+1 C．a2+2a+1 D．a+2 +16. x5·（x m）n的计算结果是( )A．x m+n+5B．x5mn C．x5+mn D．7. 如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤．其中正确结论的是（）A．①③④B．②④⑤C．①③⑤D．①③④⑤8. 如图，在6×6的方格纸中，每个小方格都是边长为1的正方形，其中A、B、C为格点，作△ABC的外接圆⊙O，则弧AC的长等于（）A．πB．C．D．9. 抛物线y=ax2+bx+c交x轴于A（﹣1，0），B（3，0），交y轴的负半轴于C，顶点为D．下列结论：①2a+b=0；②2c＜3b；③当m≠1时，a+b＜am2+bm；④当△ABD是等腰直角三角形时，则a=；⑤当△ABC是等腰三角形时，a的值有3个．其中正确的有（）个．A．5 B．4 C．3 D．2二、填空题10. 如果一个正方形的面积等于两个边长分别是3cm和4cm的正方形的面积的和，则这个正方形的边长为_____cm．11. 袋子中装有红、黄、绿三种颜色的小球各一个，从中任意摸出一个放回搅匀，再摸出一个球，则两次摸出的球都是黄色的概率是_____．12. 数学老师布置10道选择题作为课堂练习，科代表将全班同学的答题情况绘制成统计图（如图所示），根据统计图，全班每位同学答对的题数所组成的一组数据的中位数为__，众数为__．13. 在如图所示的正方形网格中，每个小正方形的边长为1各单位，格点三角形（顶点是网格线的交点的三角形）△ABC的顶点A，B的坐标分别为（1，4），（﹣3，1）．（1）请在网格所在的平面内作出符合上述表述的平面直角坐标系；（2）请你将A、B、C的横坐标不变，纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中，并画出△A1B1C1，其中点C1的坐标为．（3）△ABC的面积是．14. 如图，已经二次函数的图象与轴交于点，与轴的交点在和之间（不包括这两点），对称轴为直线.下列结论：①；②；③；④；⑤.其中正确结论有______.15. 如图，已知点E，F分别是?ABCD的边BC，AD上的中点，且∠BAC=90°，若∠B=30°，BC=10，则四边形AECF的面积为__．三、解答题16. 解方程（1）5x+3（2﹣x）=8（2）﹣=1．17. 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F. 已知AD=2cm，BC=5cm.（1）求证：FC=AD；（2）求AB的长.18. 为了解九年级学生的体能情况，学校组织了一次体能测试，并随机选取50名学生的成绩进行统计，得出相关统计表和统计图（其中部分数据不慎丢失，成绩等级优秀良好合格不合格人数m 30 n 5请根据图表所提供的信息回答下列问题：（1）统计表中的m= ，n= ；并补全频数分布直方图；（2）若该校九年级有500名学生，请据此估计该校九年级学生体能良好以上的学生有多少人？（3）根据以往经验，经过一段时间训练后，有60%的学生成绩可以上升一个等级，请估计经过训练后九年级学生体能达标率（成绩在良好及以上）19. 如图，已知以的边为直径作的外接圆的平分线交于，交于，过作交的延长线于．（1）求证：是切线；（2）若求的长．20. 如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈．已知篮圈中心到地面的距离为3.05米．（1）建立如图所示的直角坐标系，求抛物线的表达式；（2）该运动员身高1.7米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少？．21. 等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE 相交于点P．（1）若AE=CF；①求证：AF=BE，并求∠APB的度数；②若AE=2，试求AP?AF的值；（2）若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长．22. 如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c的对称轴为直线x=1，抛物线与x轴交于A、B两点（点A在点B的左侧），且AB=4，又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与对称轴交于点E，设点P的横坐标为t．（1）求点A的坐标和抛物线的表达式；（2）当AE：EP=1：2时，求点E的坐标；（3）记抛物线的顶点为M，与y轴的交点为C，当四边形CDEM是等腰梯形时，求t的值．。

2018年武汉市中考数学模拟试卷（一）（解答参考时间：120分钟，满分：120分）一、选择题（共10小题，每小题3分，共30分）1．武汉某天的最低气温25℃，最高气温33℃，则这天的温差是（ ）A ．6℃B ．7℃C ．8℃D ．－8℃ 2．代数式1a －4在实数范围内有意义，则实数a 的取值范围为（ ）A ．a ＝4B ．a ＞4C ．a ＜4D ．a ≠4 3．计算2x ＋3x 的结果是（ ）A ．5x 2B ．6x 2C ．5xD ．12x4．一个不透明的口袋里装有若干除颜色外完全相同的小球，其中有6个黄球，将口袋中的球摇匀，从中任意摸出一个球记下颜色后再放回，通过大量重复上述实验后发现，摸到黄球的频率稳定在30%，由此估计口袋中共有小球个数有（ ）A ．12个B ．18个C ．20个D ．24个 5．计算(a ＋1)(a －2)的结果是（ ）A ．a 2－2B ．a 2＋2C ．a 2－a －2D ．a 2＋a －2 6．点A （a ，－5）关于y 轴对称点的坐标（－2，b ），则a 、b 的值是（ ） A ．a ＝2，b ＝5 B ．a ＝2，b ＝－5 C ．a ＝－2，b ＝5 D ．a ＝－2，b ＝－5 7．如图是一个几何体的三视图，则这个几何体是（ ）A ．正方体B ．长方体C ．三棱柱D ．三棱锥 8．某社区青年志愿者小分队12名同学的年龄情况如下表：则这12A ．2，20岁 B ．2，19岁 C ．19岁，20岁 D ．19岁，19岁 9．如图，从家到电影院的路线图，规定每次只能向上或向右走，那么 小丽从家到电影院一共有（ ）不同的走法． A ．6种 B ．8种 C ．10种 D ．15种10．如图，AB 是⊙O 的直径，AT 是⊙O 的切线，BT 交⊙O 于点C ，D 是⊙O 上一点，CD 交AB 于点E ．若∠ATB ＝2∠CDO ，AB ＝30，AT ＝40，则CD 的长为（ ）A ．20B ．103C ．109D ．24二、填空题（共6个小题，每小题3分，共18分） 11．计算2＋12．化简（a a －2－4a 2－2a）的结果是 ．13．随机掷一枚质地均匀的硬币两次，落地后有一次正面朝上，一次反面朝上的概率为 ．14．如图，四边形ABCD 中，∠ACB ＝∠ADB ＝90°，∠BAC ＝30°，∠ACD ＝20°，则∠CAD 的度数为 ．15．如图，在平行四边形ABCD 中，点F 子啊AD 上，AF ＝6cm ，BF ＝12cm ，∠FBD ＝∠CBD ，点E 是BC 的中点，若点P 以1cm /秒的速度从点A 出发，沿AD 向点F 运动；点Q 同时以2cm /秒的速度从点C 出发，沿CB 向点B 运动，点P 运动到F 点时停止运动，点Q 也同时停止运动，当点P 运动 秒时，以点P 、Q 、E 、F 为顶点的四边形是平行四边形．16．已知抛物线y ＝－x 2＋(m －1)x ＋m 的顶点坐标为（x 0，y 0），当14≤y 0≤254时，m 的取值范围是 ．三、解答题（共8题，共72分）17．（本题8分）解方程组⎩⎨⎧=-=+②①33 1y x y x18．（本题8分）如图，点O 是线段AB 和线段CD 的中点，求证AD ∥BC ．19．（本题8分）中学生带手机上学的现象越来越受到社会的关注，为此某记者随机调查了某市城区若干名中学生家长对这种现象的态度（态度分为：（A ）无所谓；（B ）基本赞成；（C ）赞成；（D ）反对），并将调查结果绘制成频数折线统计图1和扇形统计图2（不完整）．请根据图中提供的信息，解答下列问题： （1）此次抽样调查中，共调查了 名中学生家长；（2）将图1的折线统计图补充完整；（3）根据抽样调查结果，请你估计该市城区6000名中学生家长中有多少名家长持反对态度？BCODA20．（本题8分）下表中有两种移动电话计费方式（1）如果每月主叫时间不超过400min，当主叫时间为多少时，两种方式收费相同？（2）如果每月主叫时间超过400min，选择哪种方式更省钱？21．（本题8分）如图，在△ABC中，∠ACB＝90°，点O在边BC上，以点O为圆心，OB为半径的⊙O 交AB于点E，D为⊙O上一点，弧BD＝弧BE．（1）如图1，若AE＝BE，求证：四边形ACDE是平行四边形；（2）如图2，若OB＝OC，BE＝2AE，求tan∠CAD的值．22．（本题10分）如图，在平面直角坐标系中，A（－2，0），B（0，－1），以AB为边画平行四边形ABCD．（1）如图1，若四边形ABCD为正方形，画出图形，并写出C，D的坐标；（2）若CD落在双曲线y＝4x上，求C，D的坐标；（3）若AB⊥BC且BC＝2AB，直接写出CD所在直线的解析式．23．（本题10分）如图1，△ABC 中，∠ACB 的平分线CE 交AB 于点E ． （1）求证：AE BE ＝AC BC；（2）如图2，AD ⊥BC 交CE 于F ，BD ＝2AD ，∠AEC ＝45°． ①求证：BE ＝2AE ； ②直接写出sin ∠ACE 的值．24．（本题12分）已知抛物线y ＝12x 2－mx ＋12m 2＋12m ＋1的顶点为A ，交y 轴于点B ．（1）求证：抛物线的顶点A 在定直线l 上，并求定值线l 的解析式；（2）当m ＝1时，直线l 交抛物线于另一点M ，交x 轴于点C ，N 为抛物线上一点，且∠NMC ＝2∠ACO ，求点N 的坐标；（3）如图2，当m ＝2时，过点A 作直线l 1（不经过点O ），分别交x 轴，y 轴于点E ，F ，点P 为对称轴右侧抛物线上的动点（点P 、A 、O 不共线），直线P A 分别交x 轴，y 轴于点G 、H ，过点P 作PK ∥y 轴交直线l 1于点K ，若AE ·AF ＝AG ·AH ，求点K 的纵坐标．。

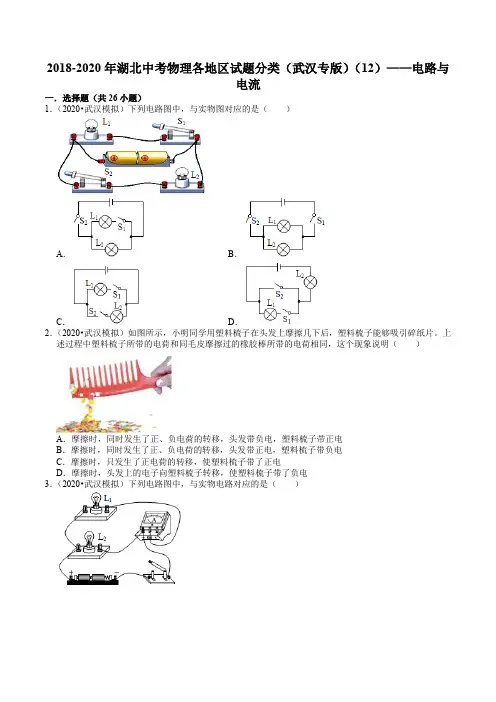
2018-2020年湖北中考物理各地区试题分类（武汉专版）（12）——电路与电流一．选择题（共26小题）1．（2020•武汉模拟）下列电路图中，与实物图对应的是（）A．B．C．D．2．（2020•武汉模拟）如图所示，小明同学用塑料梳子在头发上摩擦几下后，塑料梳子能够吸引碎纸片。

上述过程中塑料梳子所带的电荷和同毛皮摩擦过的橡胶棒所带的电荷相同，这个现象说明（）A．摩擦时，同时发生了正、负电荷的转移，头发带负电，塑料梳子带正电B．摩擦时，同时发生了正、负电荷的转移，头发带正电，塑料梳子带负电C．摩擦时，只发生了正电荷的转移，使塑料梳子带了正电D．摩擦时，头发上的电子向塑料梳子转移，使塑料梳子带了负电3．（2020•武汉模拟）下列电路图中，与实物电路对应的是（）A．B．C．D．4．（2020•武汉模拟）如图所示，验电器甲带正电，乙不带电，现用带有绝缘手柄的金属棒把甲和乙的金属球连接起来，发下甲的金属箔张角变小，乙的金属箔张开，则下列说法正确的是（）A．乙验电器金属箔张开是因为它带上了负电B．金属棒中瞬时电流的方向从乙流向甲C．部分正电荷从甲转移到乙，所以两个验电器都带正电荷D．电子从乙转移到甲，乙带正电荷5．（2020•洪山区模拟）如图所示，用一段细铁丝做一个支架，作为转动轴，把一根中间戳有小孔（没有戳穿）的饮料吸管放在转动轴上，吸管能在水平面内自由转动，用餐巾纸与吸管的一端摩擦使其带电，再用丝绸摩擦过的玻璃棒去靠近吸管，吸管两端都能与玻璃棒相互吸引。

下列说法正确的是（）A．吸管两端都带负电B．吸管两端都带正电C．吸管的一端带正电，一端不带电D．吸管的一端带负电，一端不带电6．（2020•硚口区模拟）如图所示的三个电路，下列对其通路、开路、短路判断正确的是（）A．甲开路、乙通路、丙短路B．甲通路、乙断路、丙短路C．甲通路、乙短路、丙开路D．甲短路、乙开路、丙通路7．（2019•武汉模拟）为提示视障者安全过路口的斑马线，某同学设计了带有“嘟嘟”声的交通信号灯电路：绿灯亮时电铃1响，铃声急促；红灯亮时电铃2响，铃声缓慢，红绿灯交替工作，各用电器互不影响。

2018年武汉市九年级物理中考模拟试题一、选择题(每小题只有一个选项符合题意，每小题3分，共36分)9．如图所示探究实验中，说法正确的是（）A.倒车雷达工作过程中，利用了电磁波波可以传递信息B.军事雷达是利用了次声波回声定位这一原理C.8个相同的水瓶中灌入不同高度的水，用相同的力吹奏瓶口从左到右音调越来越低D.录音棚的墙壁通常装有如图所示的皮质材料，这样做的最主要目的是减小声音的响度10．小明利用如图所示的装置进行探究“平面镜成像特点”的实验。

下列说法错误的是（）A．实验中选用玻璃板代替平面镜的目的是便于确定像的位置B．选取两支相同的蜡烛是为了比较像与物的大小关系C．蜡烛远离平面镜时，看到的像变小是因为观察的视角变大D．实验中应多次改变蜡烛A的位置，使结论具有普遍性11.在透明塑料袋子中滴几滴酒精，将袋压瘪，排尽空气后用橡皮把袋口扎紧，然后放入热水中，下列说法不正确的是（）A.装有酒精的塑料袋放入热水中鼓起，主要是因为袋内空气热胀冷缩B.从热水中拿出塑料袋，过一会就会变瘪，是因为酒精蒸气液化导致体积变小C.塑料袋放入热水后是通过热传递改变物体内能D.塑料袋放入热水后气体压强变大12.在用斜面和木块做“测量物体运动的平均速度”实验时，将带刻度的木板一端垫高做成斜面，小明用频闪照相机记录了木块沿斜面下滑的运动过程。

频闪照相机每隔0.5s拍一张照片，照片记录的木块在不同时刻的位置如图甲所示，下列分析正确的是（）A．分析照片可知AF的长度为5.5cmB．木块从A运动到F的平均速度是0.03m/sC．木块下滑过程中受平衡力的作用D．木块沿斜面下滑过程中动能增大，势能减小，机械能不变13.在卧室的中央安装一盏吊灯，要求在卧室门口及床头各安装一个开关，使这两个开关都能独立的控制这盏灯，正确的电路图是（）（图中均用电池符号表示照明电路电源）14.人类的智慧为人类的文明进步作出了巨大贡献，例如发电装置的发明、同步卫星的应用。

2018 年武汉市九年级中考数学真题模拟卷及答案分析九年级中考数学模拟试卷（120 分卷）一、选择题（本大题共10 小题，每题 3 分，共 30 分）1．9 的平方根为（）A．3 B．﹣3 C．± 3 D．2．若分式存心义，则 x 的取值范围是（）A．x≠1 B．x=2 C． x≠ 2D．x＞23．以下式子计算结果为 x2﹣ 4 的是（）A．（x+1）（x﹣ 4）B．（x+2）（x﹣2）C．（x+2）（ 2﹣ x）D．（x﹣2）24．小伟掷一枚质地均匀的骰子，骰子的六个面上分别刻有 1 到 6 的点数，以下事件是随机事件的是（）A．掷一次骰子，在骰子向上的一面上的点数大于 0B．掷一次骰子，在骰子向上的一面上的点数为 7C．掷三次骰子，在骰子向上的一面上的点数之和恰好为18D．掷两次骰子，在骰子向上的一面上的点数之积恰好是115．以下运算中，计算正确的选项是（）A．2a?3a=6a B．（3a2）3=27a6 C． a4÷a2=2a D．（ a+b）2=a2+ab+b26．在平面直角坐标系中，点A（﹣ 1，5），将点 A 向右平移 2 个单位、再向下平移 3 个单位获得点 A1；再将线段 OA1绕原点 O 顺时针旋转 90°获得 OA2．则 A2的坐标为（）A．（﹣ 1，2） B．（2，1） C．（2，﹣ 1） D．（3，﹣ 1）7．图中三视图对应的正三棱柱是（）A．B．C．D．8．为了认识某班同学一周的课外阅读量，任选班上15名同学进行检查，统计如表，则以下说法错误的选项是（）阅读量（单位：本/0123 4周）人数（单位：人）1462 2A．中位数是 2 B．均匀数是 2 C．众数是 2D．极差是 29．在平面直角坐标系中，点A、B 的坐标分别为（﹣ 3，0）、（ 3，0），点 P 在反比率函数 y=的图象上．若△ PAB为直角三角形，则知足条件的点P 的个数为（）10．假如函数 y=2x2﹣ 3ax+1，在自变量 x 的值知足 1≤x≤3 的状况下，与其对应的函数值 y 的最小值为﹣ 23，则 a 的值为（）A．B．C．或D．二、填空题（本大题共 6 小题，每题 3 分，共 18 分）11．计算式子﹣ 2﹣（ +3）的结果为．12．计算﹣的结果是．13．袋中有三个小球，分别为 1 个红球和 2 个黄球，它们除颜色外完好同样．随机拿出一个小球而后放回，再随机拿出一个小球，则两次拿出的小球颜色不同样的概率为．14．如图，把一张长方形纸条ABCD沿 EF折叠，若∠ 1=50°，则∠ AEG=．15．如图，点 A 的坐标为（ 0，1），点 B 是 x 轴正半轴上的一动点，以AB 为边作等腰直角△ ABC，使∠ BAC=90°，取 BC的中点 P．当点 B 从点 O 向 x 轴正半轴挪动到点 M （2，0）时，则点 P 挪动的路线长为．16．定义函数 f（ x），当 x≤ 3 时，f（x）=x2﹣ 2x，当 x＞3 时，f（x）=x2﹣10x+24，若方程 f（x）=2x+m 有且只有两个实数解，则m 的取值范围为．三、解答题（本大题共8 小题，共 72 分）17．解方程： 5x﹣ 1=3（x﹣1）18．如图， AC和 BD 订交于点 O，OA=OC，OB=OD，求证： AB∥CD．19．为了促使学生多样化发展，某校组织展开了社团活动，分别设置了体育类、艺术类、文学类及其余类社团（要求人人参加社团，每人只好选择一项）．为认识学生喜爱哪一种社团活动，学校做了一次抽样检查．依据采集到的数据，绘制成以下两幅不完好的统计图，请依据图中供给的信息，达成以下问题：（1）此次共检查了多少人？（2）求文学社团在扇形统计图中所占圆心角的度数（3）若该校有 1500 名学生，请预计喜爱体育类社团的学生有多少人？20．某商铺购置 60 件 A 商品和 30 件 B 商品共用了 1080 元，购置 50 件 A 商品和20 件 B 商品共用了 880 元（ 1） A 商品的单价是元，B商品的单价是元（ 2）已知该商铺购置 B 商品的件数比购置 A 商品的件数的 2 倍少 4 件，设购置A 商品的件数为x 件，该商铺购置的A、B 两种商品的总花费为y 元①求 y 与 x 的函数关系式②假如需要购置A、B 两种商品的总件数许多于32 件，且该商铺购置的A、B 两种商品的总花费不超出296 元，求购置 B 商品最多有多少件？21．如图，⊙ O 与直线 l 相离， OA⊥l 于点 A，OA 交⊙ O 于点 C，过点 A 作⊙ O 的切线 AB，切点为 B，连结 BC交直线 l 于点 D（1）求证： AB=AD；（2）若 tan∠OCB=2，⊙ O 的半径为 3，求 BD 的长．22．如图，在平面直角坐标系中， O 为坐标原点，△ ABO的边 AB 垂直于 x 轴，垂足为点 B，反比率函数 y= （x＞0）的图象经过 AO 的中点 C，且与 AB 订交于点 D，OB=4，AD=3（1）求反比率函数 y= 的分析式；（2）若直线 y=﹣x+m 与反比率函数 y= （ x＞ 0）的图象订交于两个不一样点 E、F（点 E 在点 F 的左侧），与 y 轴订交于点 M①则 m 的取值范围为（请直接写出结果）②求 ME?MF 的值．23．已知△ ABC是等腰直角三角形，∠ A=90°，D 是腰 AC上的一个动点，过 C作CE垂直于 BD 的延伸线，垂足为 E，如图 1（ 1）求证： AD?CD=BD?DE；（ 2）若 BD 是边 AC的中线，如图 2，求的值；（ 3）如图 3，连结 AE．若 AE=EC，求的值．24．如图，抛物线 y= x2+x﹣（k＞0）与x轴交于点A、B，点A在点B的右侧，与 y 轴交于点 C（1）如图 1，若∠ ACB=90°①求 k 的值；②点 P 为 x 轴上方抛物线上一点，且点P 到直线 BC的距离为，则点P的坐标为（请直接写出结果）（ 2）如图 2，当 k=2 时，过原点 O 的任向来线 y=mx（ m≠0）交抛物线于点 E、F （点 E 在点 F 的左侧）①若 OF=2OE，求直线 y=mx 的分析式；②求+的值．2018 年湖北省武汉市中考数学展望试卷参照答案与试题分析一、选择题（本大题共10 小题，每题 3 分，共 30 分）1．9 的平方根为（）A．3B．﹣3 C．± 3 D．【考点】 21：平方根．【剖析】依据平方根的定义求解即可，注意一个正数的平方根有两个．【解答】解： 9 的平方根有：=± 3．应选 C．2．若分式存心义，则 x 的取值范围是（）A．x≠1 B．x=2 C． x≠ 2D．x＞2【考点】 62：分式存心义的条件．【剖析】依据分母不等于0 列式计算即可得解．【解答】解：依据题意得， x﹣2≠0，解得 x≠2．应选： C．2﹣ 4 的是（）．以下式子计算结果为3xA．（x+1）（x﹣ 4） B．（x+2）（x﹣2） C．（x+2）（ 2﹣ x） D．（x﹣2）2【考点】 4I：整式的混淆运算．【剖析】各项计算获得结果，即可作出判断．【解答】解： A、原式 =x2﹣3x﹣4，不切合题意；2C、原式 =4﹣ x2，不切合题意；D、原式 =x2﹣4x+4，不切合题意，应选B4．小伟掷一枚质地均匀的骰子，骰子的六个面上分别刻有 1 到 6 的点数，以下事件是随机事件的是（）A．掷一次骰子，在骰子向上的一面上的点数大于0B．掷一次骰子，在骰子向上的一面上的点数为7C．掷三次骰子，在骰子向上的一面上的点数之和恰好为18D．掷两次骰子，在骰子向上的一面上的点数之积恰好是11【考点】 X1：随机事件．【剖析】依据必定事件、不行能事件、随机事件的观点以及事件发生的可能性大小判断即可．【解答】解：掷一次骰子，在骰子向上的一面上的点数大于0 是必定事件；掷一次骰子，在骰子向上的一面上的点数为7 是不行能事件；掷三次骰子，在骰子向上的一面上的点数之和恰好为 18 是随机事件；掷两次骰子，在骰子向上的一面上的点数之积恰好是 11 是不行能事件，应选：C．5．以下运算中，计算正确的选项是（）23 6C．a4÷ a2 =2a D．（a+b）2=a2 +ab+b2【考点】 4I：整式的混淆运算．【剖析】分别利用积的乘方运算法例以及同底数幂的除法运算法例、完好平方公式、单项式乘以单项式运算法例化简求出答案．2【解答】解： A、2a?3a=6a ，故此选项错误；B、（3a2）3=27a6，正确；C、a4÷ a2 =a2，故此选项错误；D、（a+b）2=a2 +2ab+b2，故此选项错误；应选：B．6．在平面直角坐标系中，点A（﹣ 1，5），将点 A 向右平移 2 个单位、再向下平移 3 个单位获得点 A1；再将线段 OA1绕原点 O 顺时针旋转 90°获得 OA2．则 A2 的坐标为（）A．（﹣ 1，2）B．（2，1） C．（2，﹣ 1）D．（3，﹣ 1）【考点】 R7：坐标与图形变化﹣旋转；Q3：坐标与图形变化﹣平移．【剖析】依据平移、中心旋转的定义画出图形，即可解决问题．【解答】解：以下图，点 A 向右平移两个单位再向下平移 3 个单位得 A1（1，2），再将线段 OA1绕原点 O 顺时针旋转 90°获得 OA2，A2坐标（ 2，﹣ 1）．应选 C．7．图中三视图对应的正三棱柱是（）A．B．C．D．【考点】 U3：由三视图判断几何体．【剖析】利用俯视图可裁减 C、D 选项，依据主视图的侧棱为实线可裁减 B，从而判断 A 选项正确．【解答】解：由俯视图获得正三棱柱两个底面在竖直方向，由主视图获得有一条侧棱在正前面，于是可判断 A 选项正确．应选 A．8．为了认识某班同学一周的课外阅读量，任选班上15名同学进行检查，统计如表，则以下说法错误的选项是（）阅读量（单位：本/0123 4周）人数（单位：人）1462 2A．中位数是 2 B．均匀数是 2 C．众数是 2D．极差是 2【考点】 W6：极差； W2：加权均匀数； W4：中位数； W5：众数．【剖析】依据表格中的数据，求出中位数，均匀数，众数，极差，即可做出判断．【解答】解：15 名同学一周的课外阅读量为 0，1，1，1，1，2，2，2，2，2，2，3，3，4，4，中位数为 2；均匀数为（ 0×1+1× 4+2×6+3×2+4× 2）÷ 15=2；众数为 2；极差为 4﹣ 0=4；因此 A、B、C 正确， D 错误．应选 D．9．在平面直角坐标系中，点A、B 的坐标分别为（﹣ 3，0）、（ 3，0），点 P 在反比率函数 y=的图象上．若△ PAB为直角三角形，则知足条件的点P 的个数为（）A．2 个 B．4 个 C．5 个 D．6 个【考点】 G6：反比率函数图象上点的坐标特点．【剖析】设点P 的坐标为（x，y），分∠APB=90°、∠PAB=90°和∠PBA=90°三种状况考虑：当∠APB=90°时，以AB 为直径作圆，由圆与双曲线无交点可知此时点 P 不存在；当∠ PAB=90°时，可找出 x=﹣3，从而可得出点 P 的坐标；当∠ PBA=90°时，可找出 x=3，从而可得出点 P 的坐标．综上即可得出结论．【解答】解：设点 P 的坐标为（ x， y），当∠ APB=90°时，以 AB 为直径作圆，以下图，∵圆与双曲线无交点，∴点P 不存在；当∠ PAB=90°时， x=﹣ 3， y==﹣3，∴点 P 的坐标（﹣ 3，﹣ 3）；当∠ PBA=90°时， x=3，y==3，∴点 P 的坐标为（ 3， 3）．综上所述：知足条件的点P有 2 个．应选 A．10．假如函数 y=2x2﹣ 3ax+1，在自变量 x 的值知足 1≤x≤3 的状况下，与其对应的函数值 y 的最小值为﹣ 23，则 a 的值为（）A．B．C．或D．【考点】 H7：二次函数的最值．【剖析】分 a＜、≤a≤4 和 a＞4 三种状况，找出函数值 y 的最小值，令其等于﹣ 23，即可得出对于 a 的一元一次（或一元二次）方程，解之即可得出结论．【解答】解：抛物线 y=2x2﹣ 3ax+1 的对称轴为 x= a．当 a＜ 1，即 a＜时，有 2﹣ 3a+1=﹣23，解得： a=（舍去）；当 1≤a≤3，即≤ a≤ 4时，有a2=24，解得： a=或a=﹣（舍去）；当 a＞ 3，即 a＞4 时，有 18﹣9a+1=﹣ 23，解得： a=．综上所述： a 的值为或．应选C．二、填空题（本大题共 6 小题，每题 3 分，共 18 分）11．计算式子﹣ 2﹣（ +3）的结果为﹣5．【考点】 1A：有理数的减法．【剖析】减去一个数，等于加上这个数的相反数．【解答】解：﹣ 2﹣（ +3）=﹣2﹣3=﹣（ 2+3）=﹣ 5，故答案为：﹣ 5．12．计算﹣的结果是．【考点】 6B：分式的加减法．【剖析】依据同分母分式加减运算法例计算即可，最后要注意将结果化为最简分式．【解答】解：原式 ===，故答案为：．13．袋中有三个小球，分别为 1 个红球和 2 个黄球，它们除颜色外完好同样．随机拿出一个小球而后放回，再随机拿出一个小球，则两次拿出的小球颜色不同样的概率为．【考点】 X6：列表法与树状图法．【剖析】依据题意列表，再依据表格即可求得全部等可能的结果与两次拿出的小球颜色同样的状况，而后依据概率公式求解．【解答】解：列表得：红黄黄红（红，红）（黄，红）（黄，红）黄（黄，红）（黄，黄）（黄，黄）黄（黄，红）（黄，黄）（黄，黄）由列表可知共有9 种可能状况，此中两次拿出的小球颜色不同样的有 4 种，因此两次拿出的小球颜色不同样的概率=，故答案为：．14．如图，把一张长方形纸条ABCD沿 EF折叠，若∠ 1=50°，则∠ AEG= 80° ．【考点】 JA：平行线的性质； PB：翻折变换（折叠问题）．【剖析】依据长方形性质得出平行线，依据平行线的性质求出∠ DEF，依据折叠求出∠ FEG，即可求出答案．【解答】解：∵四边形 ABCD是长方形，∴ AD∥ BC，∴∠DEF=∠1=50°，∵沿 EF折叠 D 到 D′，∴∠ FEG=∠ DEF=50°，∴∠AEG=180°﹣ 50°﹣ 50°=80°，故答案为： 80°．15．如图，点 A 的坐标为（ 0，1），点 B 是 x 轴正半轴上的一动点，以 AB 为边作等腰直角△ ABC，使∠ BAC=90°，取 BC的中点 P．当点 B 从点 O 向 x 轴正半轴挪动到点 M （2，0）时，则点 P 挪动的路线长为．【考点】O4：轨迹；D5：坐标与图形性质； KD：全等三角形的判断与性质； KW：等腰直角三角形； LF：正方形的判断．【剖析】先过 P 作 PD⊥x 轴于 D，作 PE⊥y 轴于 E，依据△ AEP≌△ BDP（AAS），得出 PE=PD，从而获得点 P 的运动路径是∠ AOM 的角均分线，再分别求适当点B与点 O 重合时， OP= OC=，当点B与点M重合时，OP=OD=，从而获得点 P 挪动的路线长．【解答】解：以下图，过 P 作 PD⊥x 轴于 D，作 PE⊥y 轴于 E，则∠ DPE=90°，∠AEP=∠BDP=90°，连结 AP，∵△ ABC是等腰直角三角形， P 是 BC的中点，∴AP= BC=BP，且 AP⊥BC，即∠ APB=90°，∴∠ APE=∠BPD，在△ AEP和△ BDP中，，∴△ AEP≌△ BDP（ AAS），∴ PE=PD，∴点 P 的运动路径是∠ AOM 的角均分线，以下图，当点 B 与点 O 重合时， AB=AO=1， OC=，∴ OP= OC=；以下图，当点 B 与点 M 重合时，过 P 作 PD⊥x 轴于 D，作 PE⊥y 轴于 E，连结OP，由△ AEP≌△ BDP，可得 AE=BD，设 AE=BD=x，则 OE=1+x，OD=2﹣x，∵矩形 ODPE中， PE=PD，∴四边形 ODPE是正方形，∴ OD=OE，即 2﹣ x=1+x，解得 x=，∴ OD=2﹣=，∴等腰 Rt△OPD中， OP= OD=，∴当点 B 从点 O 向 x 轴正半轴挪动到点 M 时，则点 P 挪动的路线长为﹣=．故答案为：．．定义函数（），当≤时，（）2﹣ 2x，当 x＞3 时，f（x）=x2﹣10x+24，16 f x x 3 f x =x m＞﹣ 3 或﹣ 12若方程f（x）=2x m 有且只有两个实数解，则 m 的取值范围为+＜ m＜﹣ 4 ．【考点】 HA：抛物线与 x 轴的交点．【剖析】分别画出 x≤ 3 和 x＞3 的函数图象，得出两抛物线的交点坐标（3，3），联合函数图象知①直线f（x）=2x+m 过点（ 3，3）时；②当直线 f（ x）=2x+m 与f（x）=x2﹣2x 只有一个交点时，方程只有一个实数解，分别求出m 的值，联合函数图象可得 m 的取值范围．【解答】解：∵ x≤3 时， f（ x） =x2﹣ 2x=（ x﹣ 1）2﹣1，当 f（ x）=0 时，由 x2﹣ 2x=0 得 x=0 或 x=2，∴抛物线与 x 轴的交点为（ 0，0）和（ 2，0），∵x＞3 时， f （x） =x2﹣ 10x+24=（ x﹣5）2﹣1，∴此时抛物线的极点坐标为（5，﹣ 1），当 f（ x）=0 时，由 x2﹣ 10x+24=0 得 x=4 或 x=6，∴此时抛物线与 x 轴的交点为（ 4，0）和（ 6，0），由可得，即两抛物线交点坐标为（3，3），以下图：直线 f （x） =2x+m 可看作直线 y=2x平移获得，①当直线 f（ x）=2x+m 过点（ 3，3），即 6+m=3，得 m=﹣3 时，直线 f （x） =2x+m 与 f（x）=x2﹣2x 的图象有两个交点；②当直线 f（ x） =2x+m 与 f（x） =x2﹣ 2x 有一个交点，即 x2﹣2x=2x+m 只有一个解时，方程 f （x） =2x+m 有且只有两个解，解得： m=﹣4，当直线 f（x）=2x+m 与 f（x）=x2﹣ 10x+24 只有 1 个交点时，即 2x+m=x2﹣10x+24 只有一个解，解得： m=﹣12，由图象可知当 m＞﹣ 3 或﹣ 12＜ m＜﹣ 4 时，方程 f（ x） =2x+m 有且只有两个实数解，故答案为： m＞﹣ 3 或﹣ 12＜ m＜﹣ 4．三、解答题（本大题共8 小题，共 72 分）17．解方程： 5x﹣ 1=3（x﹣1）【考点】 86：解一元一次方程．【剖析】依据去括号，移项，归并同类项，可得答案．【解答】解：去括号，得5x﹣ 1=3x﹣ 3，移项，归并同类项，得﹣ 2x=﹣ 2，系数化为 1，得 x=﹣1．18．如图， AC和 BD 订交于点 O，OA=OC，OB=OD，求证： AB∥CD．【考点】 KD：全等三角形的判断与性质；J9：平行线的判断．【剖析】依据条件证明△ AOB≌△ COD就能够得出∠ A=∠C 就能够得出结论．【解答】证明：在△ AOB和△ COD中，∴△ AOB≌△ COD（SAS），∴∠ A=∠C，∴ AB∥CD．19．为了促使学生多样化发展，某校组织展开了社团活动，分别设置了体育类、艺术类、文学类及其余类社团（要求人人参加社团，每人只好选择一项）．为认识学生喜爱哪一种社团活动，学校做了一次抽样检查．依据采集到的数据，绘制成以下两幅不完好的统计图，请依据图中供给的信息，达成以下问题：（1）此次共检查了多少人？（2）求文学社团在扇形统计图中所占圆心角的度数（3）若该校有 1500 名学生，请预计喜爱体育类社团的学生有多少人？【考点】 VC：条形统计图； V5：用样本预计整体； VB：扇形统计图．【剖析】（1）由体育社团的人数除以占的百分比，确立出共检查的人数即可；（ 2）由文学社团的人数除以总人数，再乘以360°即可获得结果；（3）由体育社团的百分比乘以 1500 即可获得结果．【解答】解：（1）依据题意得： 80÷40%=200（人），则此次共检查了 200 人；（2）依据题意得： 60×200×360°=108°，则文学社团在扇形统计图中所占的圆心角度数为108°；（3）依据题意得： 1500×40%=600（人），则喜爱体育类社团的学生约有 600人．20．某商铺购置 60 件 A 商品和 30 件 B 商品共用了 1080 元，购置 50 件 A 商品和20 件 B 商品共用了 880 元（1） A 商品的单价是 16 元， B 商品的单价是 4 元（2）已知该商铺购置 B 商品的件数比购置 A 商品的件数的 2 倍少 4 件，设购置A 商品的件数为x 件，该商铺购置的A、B 两种商品的总花费为y 元①求 y 与 x 的函数关系式②假如需要购置 A、B 两种商品的总件数许多于 32 件，且该商铺购置的 A、B 两种商品的总花费不超出 296 元，求购置 B 商品最多有多少件？【考点】 FH：一次函数的应用； CE：一元一次不等式组的应用．【剖析】（1）依据题意能够列出相应的二元一次方程组，从而能够解答本题；（2）①依据题意能够获得 y 与 x 的函数关系式；②依据题意能够列出相应的不等式组，从而能够解答本题．【解答】解：（1）A 商品的单价是 x 元， B 商品的单价是 y 元，，解得，即 A 商品的单价是 16 元， B 商品的单价是 4 元，故答案为： 16， 4；（ 2）①由题意可得，y=16x+4（2x﹣ 4） =24x﹣16，即 y 与 x 的函数关系式是y=24x﹣16；②由题意可得，，解得， 12≤x≤ 13，∴ 20≤2x﹣4≤22，∴购置 B 商品最多有 22 件，答：购置 B 商品最多有 22 件．21．如图，⊙ O 与直线 l 相离， OA⊥l 于点 A，OA 交⊙ O 于点 C，过点 A 作⊙ O 的切线 AB，切点为 B，连结 BC交直线 l 于点 D（1）求证： AB=AD；（2）若 tan∠OCB=2，⊙ O 的半径为 3，求 BD 的长．【考点】 MC：切线的性质； T7：解直角三角形．【剖析】（ 1）连结 OB，利用切线的性质以及等腰三角形的性质证明∠ ADB=∠ABD，利用等角平等边证得；（ 2）设 AC=a，则 AB=AD=2a，在 Rt△AOB 中利用勾股定理即可列方程求得 a 的值，从而求得 BD 的长．【解答】解：（1）证明：连结 OB．∵ AB是⊙ O 的切线， OA⊥l，∴∠ OBA=∠OAD=90°，又 OB=OC，∴∠ OBC=∠COB=∠ACD，∴∠ ADB=∠ ABD，∴AB=AD；（ 2）∵ tan∠OCB=tan∠ACD= =2，⊙ O 的半径是 3，设 AC=a，则 AB=AD=2a，在 Rt△AOB中， OA2 =AB2+OB2，∴（ a+3）2=（ 2a）2+32，∴ a=2．过点 A 作 AE⊥ BD，设 AE=x，DE=2x，则 5x2=16，x=，∴BD=BE=，∴ BD=．22．如图，在平面直角坐标系中，O 为坐标原点，△ ABO的边 AB 垂直于 x 轴，垂足为点 B，反比率函数 y= （x＞0）的图象经过 AO 的中点 C，且与 AB 订交于点 D，OB=4，AD=3（1）求反比率函数 y= 的分析式；（2）若直线 y=﹣x+m 与反比率函数 y= （ x＞ 0）的图象订交于两个不一样点 E、F（点 E 在点 F 的左侧），与 y 轴订交于点 M①则 m 的取值范围为m＞4（请直接写出结果）②求 ME?MF 的值．【考点】 G8：反比率函数与一次函数的交点问题．【剖析】（1）设 D 的坐标是（ 4，a），则 A 的坐标是（ 4，a+3），由点 C 是 OA 的中点，可用含 a 的代数式表示出点 C 的坐标，再依据反比率函数图象上点的坐标特点即可找出4a=2×=k，解之即可得出a、 k 的值，从而即可得出反比率函数的分析式；（ 2）①将一次函数分析式代入反比率函数分析式中，整理后可得出对于x 的一元二次方程，由m＞0 以及根的鉴别式△＞ 0，即可得出对于m 的不等式组，解之即可得出结论；②由一次函数分析式可得出∠MEG=∠MFH=45°，从而可得出 ME=GE、MF= HF，将一次函数分析式代入反比率函数分析式中，由根与系数的关系可得出x E?x F=4，从而可得出 ME?MF=2x E?x F=8，本题得解．【解答】解：（1）设 D 的坐标是（ 4，a），则 A 的坐标是（ 4，a+3）．又∵点 C 是 OA 的中点，∴点 C 的坐标是（ 2，），∴ 4a=2×=k，解得 a=1， k=4，∴反比率函数的分析式为y=；（2）①将 y=﹣x+m 代入 y= 中，﹣ x+m= ，整理，得： x2﹣mx+4=0，∵直线 y=﹣x+m 与反比率函数 y= （ x＞0）的图象订交于两个不一样点 E、F，∴，解得： m＞4．故答案为： m＞ 4．②过点 E、 F 分别作 y 轴的垂线，垂足分别为G、H．由 y=﹣x+m 可知：∠ MEG=∠MFH=45°，∴ ME= GE，MF= HF．由 y=﹣x+m=，得x2﹣mx+4=0，∴ x E?x F=4，∴ ME?MF=2x E?x F=8．23．已知△ ABC是等腰直角三角形，∠ A=90°，D 是腰 AC上的一个动点，过 C 作CE垂直于 BD 的延伸线，垂足为 E，如图 1（ 1）求证： AD?CD=BD?DE；（ 2）若 BD 是边 AC的中线，如图 2，求的值；（ 3）如图 3，连结 AE．若 AE=EC，求的值．【考点】 SO：相像形综合题．【剖析】（1）直接判断出△ ABD∽△ ECD，即可得出结论；（ 2）先设 AB=AC=2a，CD=a，则 BC=a， AD=a．求出 BD，而△ BAD∽△ CED，得出，代入求出 CE即可解决问题．（ 2）如图 3，延伸 CE、BA 订交于点 F．只需证明△ BEC≌△ BEF，推出CE=EF，CF=2CE，由 ABD≌△ ACF，推出 BD=CF，即可解决问题．【解答】解：（1）∵ CE⊥ BD，∴∠ A=∠E=90°，∵∠ ADB=∠EDC，∴△ BAD∽△ CED，∴，∴ AD?CD=BD?DE；（2）设 CD=AD=a，则 AB=AC=2a．在 Rt△ABD 中，由勾股定理得： BD=a，由（ 1）知，△ BAD∽△ CED，∴，∴，解得： CE=a，∴==；（ 3）如图 3，延伸 CE、BA 订交于点 F．∵ BE是∠ ABC的角均分线，且BE⊥ CF在△ BEC和△ BEF中，，∴△ BEC≌△ BEF，∴ CE=EF，∴ CF=2CE又∵∠ ABD+∠ADB=∠ CDE+∠ACF=90°，且∠ ADB=∠CDE，∴∠ ABD=∠ ACF ∵AB=AC，∠ BAD=∠CAF=90°，在△ ABD和△ ACF中，，∴△ ABD≌△ ACF（ASA），∴ BD=CF，∴ BD=2CE，∴=2．24．如图，抛物线 y= x2+x﹣（k＞0）与x轴交于点A、B，点A在点B的右侧，与 y 轴交于点 C（1）如图 1，若∠ ACB=90°①求 k 的值；②点 P 为 x 轴上方抛物线上一点，且点P 到直线 BC的距离为，则点P的坐标为（﹣ 4﹣，）（请直接写出结果）（ 2）如图 2，当 k=2 时，过原点 O 的任向来线 y=mx（ m≠0）交抛物线于点E、F（点 E 在点 F 的左侧）①若 OF=2OE，求直线 y=mx 的分析式；②求+的值．【考点】 HF：二次函数综合题．【剖析】（1）①选将函数关系式变形为y=（x﹣2）（x+k），从而可获得点A 和点 B 的坐标，而后再求得点 C 的坐标，接下来再证明△ OBC ∽△ OCA ，依照相像三角形的性质可获得 OC 2=AO?OB ，从而列出对于 k 的方程，故此可求得 k 的值；②将 k=8 代入抛物线的分析式得： y=x 2+ x ﹣ 4，而后再求得点 A 、B 、C 的坐标，依照勾股定理可求得 AC 的长，由点 B 和点 C 的坐标可求得 BC 的分析式，设 M为 AC 的中点，则 M （1，﹣2），过点 M 作 PM ∥ BC ，交抛物线与点 P ．而后求得 PM 的分析式，最后求得 PM 与抛物线的交点 P 的坐标即可；（ 2）①过点 E 、F 分别作 x 轴的垂线，垂直分别为 M ，N ．把 k=2 代入得： y= x2﹣ 1．将 y=mx 代入得：x 2﹣ 1=mx ，依照一元二次方程根与系数的关系获得x E +x F =4m ， x E ?x F =﹣4，由 OF=2OE ，可获得 x F =﹣ 2x E ，从而可求得 m 的值； ②设∠ FON=α，则 +=cos α（ + ）．由直线的分析式可知 cos α=，而后依照一元二次方程根与系数的关系获得 +=，故此可求得问题的答案．【解答】 解：（1）①∵ y=[ x 2+（k ﹣2）x ﹣ 2k] = （x ﹣ 2）（x+k ），∴点 A 的坐标为（ 2，0），点 B 的坐标为（﹣ k ，0）．∵将 x=0 代入抛物线的分析式为 y=﹣ ．∴点 C 的坐标为（ 0，﹣）．∵∠ BCO+∠ACO=90°，∠ OBC+∠ BCO=90°，∴∠ OBC=∠ OCA ． 又∵∠ BOC=∠AOC ，∴△ OBC ∽△ OCA ．∴=．∴ OC 2．=AO?OB∴ k 2，解得：k=8 或 （舍去）．=2kk=0②将 k=8 代入抛物线的分析式得： y= x 2+ x ﹣4．当 x=0 时， y=﹣4，∴ C （ 0，﹣ 4）．令 y=0 得： x 2+ x ﹣4=0，解得 x=﹣8 或 x=2．∴ A （2，0）B （﹣ 8， 0）．∴ AC==2．设直线 BC 的分析式为 y=kx+b ，将点 B 和点 C 的坐标代入得：，解得：，∴直线 BC 的分析式为 y=x ﹣ 4．设 M 为 AC 的中点，则 M （1，﹣ 2），如图 1 所示：过点 M 作 PM ∥BC ，交抛物线与点 P ．设直线 PM 的分析式为 y=﹣x+c，将点 M 的坐标代入得：﹣+c=﹣ 2，解得：c=﹣．∴直线 PM 的分析式为 y=﹣x﹣．∴﹣x﹣= x2+ x﹣ 4，解得 x=﹣4﹣或x=﹣4+（舍去）．当 x=﹣4﹣时，y=．∴点P的坐标为（﹣4﹣，）．故答案为：（﹣ 4﹣，）．（ 2）①过点 E、 F 分别作 x 轴的垂线，垂直分别为M ， N．把 k=2 代入得： y= x2﹣1．由x2﹣1=mx，获得 x E+x F=4m，x E?x F=﹣4．∵OF=2OE，∴ x F=﹣2x E，且 x E＜0，∴﹣ 2x E?x E=﹣4，解得： x E=﹣．∴﹣+2 =4m，解得： m=．②设∠ FON=α，则+ =cosα（+）．∵直线 EF的分析式为 y=mx，∴ tan α=m，∴ cosα=．∴+ ====．∴+ =cosα（+）=?=1．。

、-、-2C．-D．-、--12．化简：-b13．在－1、0、、1、2、3中任取两个数，两数相乘结果是无理数的概率是__________2018武汉中考数学模拟题一一、选择题（共10小题，每小题3分，共30分）1．25的平方根为（）A．5B．±5C．－5D．±42．如果分式A．x≠0xx-1无意义，那么x的取值范围是（）B．x＝1C．x≠1D．x＝－13．(－a＋3)2的计算结果是（）A．－a2＋9B．－a2－6a＋9C．a2－6a＋9D．a2＋6a＋94．在不透明的布袋中，装有大小、形状完全相同的3个黑球、2个红球，从中摸一个球，摸出的是个黑球，这一事件是（）A．必然事件B．随机事件C．确定事件D．不可能事件5．下列运算结果是a6的是（）A．a3·a3B．a3＋a3C．a6÷a3D．(－2a2)36．将点A(1，－2)绕原点逆时针旋转90°得到点B，则点B的坐标为（）A．(－1，－2)B．(2，1)C．(－2，－1)D．(1，2)7．由6个大小相同的小正方体组合成一个几何体，其俯视图如图所示，其中正方形中的数字表示该位置放置的小正方体的个数，则该几何体的主视图为（）8．在我市开展的“好书伴我成长”读书活动中，学校随机调查了九年级50名学生读书的册数统计数据如下表所示，那么这50名学生读书册数的平均数与中位数分别为（）册数人数311321631741A．2和3B．3和3C．2和2D．3和29．在如图的4×4的方格中，与△ABC相似的格点三角形（顶点均在格点上）（且不包括△ABC）的个数有（）A．23个B．24个C．31个D．32个10．二次函数y＝mx2－nx－2过点(1，0)，且函数图象的顶点在第三象限．当m＋n为整数时，则mn的值为（）A．-1322B．-1、34132434、2二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：－7－2＝__________1-b+1b+1＝__________1314．如图，△ABC中，AB＝AC，∠BAC＝66°，OD垂直平分线段AB，AO平分∠BAC，将∠C沿EF（点E在BC 上，点F在AC上）折叠，点C与点O恰好重合，则∠OEC＝___________=，AD＝7，A⎩3x-y=1615．如图，在四边形ABCD中，AC与BD交于点O，∠DAB与∠ACB互补，C＝6，AB＝8，则BC＝___________OD5OB316．如图，C是半径为4的半圆上的任意一点，AB为直径，延长AC至点P使CP＝2CA．当点C从B运动到A时，动点P的运动路径长为___________三、解答题（共8题，共72分）⎧x+2y=317．（本题8分）解方程组：⎨18．（本题8分）如图，已知点E、C在线段BF上，BE＝CF，AB∥DE，AC∥DF，求证：ABC≌△DEF△19．（本题8分）某校体育组对本校九年级全体同学体育测试情况进行调查，他们随机抽查部分同学体育测试成绩（由高到低分四个等级），根据调查的数据绘制成如下的条形统计图和扇形统计图请根据以上不完整的统计图提供的信息，解答下列问题：(1)该课题研究小组共抽查了__________名同学的体育测试成绩，扇形统计图中B级所占的圆心角是__________(2)补全条形统计图(3)若该校九年级共有200名同学，请估计该校九年级同学体育测试达标（测试成绩C级以上，含C 级）均有名20．（本题8分）某校安排6名教师和300名学生春游，准备租用45座大客车和30座的小客车．若租用1辆大客车和2辆小客车共需租金960元；若租用2辆大客车和1辆小客车共需租金1080元(1)求1辆大客车和1辆小客车的租金各为多少元？(2)若总共租用8辆客车，总费用不超过3080元，问有几种租车方案，最省钱的方案是哪种？21．（本题8分）如图，BC为⊙O的直径，点A为⊙O上一点，点E△为ABC的内心，OE⊥EC(1)若BC＝10，求DE的长(2)求sin∠EBO的值22．（本题10分）如图，直线y＝2x与函数y k（x＞0）的图象交于第一象限的点A，且A点的x横坐标为1，过点A作AB⊥x轴于点B，C为射线BA上一点，作CE⊥AB交双曲线于点E，延长OC 交AE于点F(1)则k＝__________(2)作EM∥y轴交直线OA于点M，交OC于点G①求证：AF＝FE②比较MG与EG的大小，并证明你的结论(2)若点G在线段EF上，点D在线段BC上，且GF==，α＝90°，EB＝1，求线段GD的长23．（本题10分）如图，在△ABC△与AFE中，AC＝2AB，AF＝2AE，∠CAB＝∠FAE＝α(1)求证：∠ACF＝∠ABECD1EF CB3(3)将(2)中改为120°，其它条件不变，请直接写出GDCF的值24．（本题12分）在平面直角坐标系中，抛物线C1：y＝ax2＋bx－1的最高点为点D(－1，0)，将C1左移1个单位，上移1个单位得到抛物线C2，点P为C2的顶点(1)求抛物线C1的解析式(2)若过点D的直线l与抛物线C2只有一个交点，求直线l的解析式(3)直线y＝x＋c与抛物线C2交于D、B两点，交y轴于点A，连接AP，过点B作BC⊥AP于点C，点Q为C2上PB之间的一个动点，连接PQ交BC于点E，连接BQ并延长交AC于点F，试说明：FC·(AC＋E C)为定值2018武汉中考数学模拟题二一、选择题（共10小题，每小题3分，共30分）1．64的算术平方根是（）A．8B．－8C．4D．－42．要使分式5x1有意义，则x的取值范围是（）A．x≠1B．x＞1C．x＜1D．x≠－13．下列计算结果为x8的是（）A．x9－x B．x2·x4C．x2＋x6D．(x2)44．有两个事件，事件A：投一次骰子，向上的一面是3；事件B：篮球队员在罚球线上投篮一次，投中，则（）A．只有事件A是随机事件C．事件A和B都是随机事件5．计算(a－3)2的结果是（）B．只有事件B是随机事件D．事件A和B都不是随机事件A．a2－4B．a2－2＋4C．a2－4a＋4D．a2＋46．如图，将△AOB绕点O逆时针旋转90°，得到△A′OB′．若点A的坐标为(a，b)，则点A′的坐标为（）A．(a，b)B．(－a，b)C．(b，－a)D．(－b，a)7．如图是由一些小正方体组合而成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，则这个几何体主视图是（）8．某小组5名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是（）劳动时间（小时）人数313.51424.51A．中位数是4，平均数是3.75C．中位数是4，平均数是3.8B．众数是4，平均数是3.75D．众数是2，平均数是3.89．把所有正奇数从小到大排列，并按如下规律分组：(1)(3，5，7)、(9，11，13，15，17)，(19，21，23，25，27，29，31)，……，现有等式Am＝(i，j)表示正奇数m是第i组第j个数（从左往右数），如A7＝(2，3)，则A89＝（）A．(6，7)B．(7，8)C．(7，9)D．(6，9)10．二次函数y＝2x2－2x＋m（0＜m＜y的取值范围为（）A．y＜0B．0＜y＜m12），如果当x＝a时，y＜0，那么当x＝a－1时，函数值C．m＜y＜m＋4D．y＞m二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：(－3)＋8＝___________12．计算：a⎩3x+2y=81+a-1a-1＝___________13．不透明的袋子中有6个除了颜色不同其他都一样的球，其中有3个黑球，2个白球，1个红球．拿出两个球，颜色相同的概率是___________14．如图，E是矩形ABCD的对角线的交点，点F在边AE上，且DF＝DC．若∠ADF＝25°，则∠BEC＝__________15．如图，从一张腰为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用次剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为__________16．已知OM⊥ON，斜边长为4的等腰直角△ABC的斜边AC在射线ON上，顶点C与O重合．若点A沿NO方向向O运动，△ABC的顶点C随之沿OM方向运动，点A移动到点O为止，则直角顶点B运动的路径长是__________三、解答题（共8题，共72分）⎧2x-y=317．（本题8分）解方程组：⎨18．（本题8分）已知：如图，点B、F、C、E在一条直线上，BF＝CE，AC＝DF，且AC∥DF，求证：∠B＝∠E19．（本题8分）某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费，为更好地决策，自来水公司的随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图，（每组数据包括在右端点但不包括左端点），请你根据统计图解答下列问题：(1)此次抽样调查的样本容量是___________(2)补全频数分布直方图，求扇形图中“15吨～20吨”部分的圆心角的度数(3)如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？20．（本题 8 分）荔枝是深圳的特色水果，小明的妈妈先购买了 2 千克桂味和 3 千克糯米糍，共 花费 90 元；后又购买了 1 千克桂味和 2 千克糯米糍，共花费 55 元．（每次两种荔枝的售价都不 变）(1) 求桂味和糯米糍的售价分别是每千克多少元(2) 如果还需购买两种荔枝共 12 千克，要求糯米糍的数量不少于桂味数量的 2 倍，请设计一种 购买方案，使所需总费用最低21．（本题 8 分）如图，直径 AE 平分弦 CD ，交 CD 于点 G ，EF ∥CD ，交 AD 的延长线于 F ，AP ⊥ AC 交 CD 的延长线于点 P (1) 求证：EF 是⊙O 的切线(2) 若 AC ＝2，PD ＝ 1CD ，求 tan ∠P 的值222．（本题 10 分）已知，直线 l 1：y ＝－x ＋n 过点 A (－1，3)，双曲线 C ： y m x（x ＞0），过点B (1，2)，动直线 l 2：y ＝kx －2k ＋2（k ＜0）恒过定点 F (1) 求直线 l 1，双曲线C 的解析式，定点 F 的坐标(2) 在双曲线 C 上取一点 P (x ，y )，过 P 作 x 轴的平行线交直线 l 1 于 M ，连接 PF ，求证：PF ＝PM (3) 若动直线 l 2 与双曲线 C 交于 P 1、P 2 两点，连接 OF 交直线 l 1 于点 E ，连接 P 1E 、P 2E ，求证：EF 平分∠P 1EP 223．（本题10分）已知△ABC中，D为AB边上任意一点，DF∥AC交BC于F，AE∥BC，∠CDE ＝∠ABC＝∠ACB＝α(1)如图1，当α＝60°时，求证：△DCE是等边三角形(2)如图2，当α＝45°时，求证：①CD2；②CE⊥DE DE(3)如图3，当α为任意锐角时，请直接写出线段CE与DE的数量关系（用α表示）24．（本题12分）在平面直角坐标系xOy中，抛物线c1：y＝ax2－4a＋4（a＜0）经过第一象限内的定点P(1)直接写出点P的坐标(2)若a＝－1，如图1，点M的坐标为(2，0)是x轴上的点，N为抛物线c1上的点，Q为线段MN的中点，设点N在抛物线c1上运动时，Q的运动轨迹为抛物线c2，求抛物线c2的解析式(3)直线y＝2x＋b与抛物线c1相交于A、B两点，如图2，直线PA、PB与x轴分别交于D、C两点，当PD＝PC时，求a的值12．计算：2x2018武汉中考数学模拟题三一、选择题（共10小题，每小题3分，共30分）1．4的值为（）A．±22．要使分式1x+3B．2C．－2D．2有意义，则x的取值应满足（）A．x≥3B．x＜3C．x≠－3D．x≠33．下列计算结果为x6的是（）A．x·x6B．(x2)3C．x7－x D．x12÷x24．袋中装有4个红球和2个黄球，这些球的形状、大小、质地完全相同．在看不到球的条件下，随机地从袋子中摸出三个球，下列事件是不可能事件的是（）A．摸出的三个球中至少有一个红球C．摸出的三个球都是红球5．计算(a－1)2正确的是（）B．摸出的三个球中有两个球是黄球D．摸出的三个球都是黄球A．a2－1B．a2－2a＋1C．a2－2a－1D．a2－a＋16．在平面直角坐标系中，将点A(x，y)向左平移5个单位长度，再向上平移3个单位长度后与点B(－3，2)重合，则点A的坐标为（）A．(3，1)B．(2，－1)C．(4，1)D．(3，2)7．如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的左视图是（）8．为调查某班学生每天使用零花钱的情况，童老师随机调查了30名同学，结果如下表：每天使用零花钱（单位：元）人数52105158209256则这30名同学每天使用的零花钱的众数和中位数分别是（）A．20、15B．20、17.5C．20、20D．15、159．正方形A1B1C1O、A2B2C2C1、A3B3C3C2、……按如图的方式放置，点A1、A2、A3……和点C1、C2、C3……分别在直线y＝x＋1和x轴上，则点B6的坐标是（）A．(31，16)B．(63，32)C．(15，8)D．(31，32)10．已知关于x的二次函数y＝x2－2x－2，当a≤x≤a＋2时，函数有最大值1，则a的值为（）A．－1或1C．－1或3B．1或－3D．3或－3二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：2－(－4)＝___________2-x-1x-1＝___________13．学校为了了解九年级学生“一分钟跳绳次数”的情况，随机选取了4名女生和2名男生，⎩3x + 2 y = 1则从这 6 名学生中选取 2 名同时跳绳，恰好选中一男一女的概率是 ___________14．如图，将矩形 ABCD 沿 BD 翻折，点 C 落在 P 点处，连接 AP ．若∠ABP ＝26°，则∠APB ＝ ___________15．已知平行四边形内有一个内角为 60°，且 60°的两边长分别为 3、4．若有一个圆与这个平行 四边形的三边相切，则这个圆的半径为___________16．如图，已知线段 AB ＝6，C 、D 是 AB 上两点，且 AC ＝DB ＝1，P 是线段 CD 上一动点，在 AB 同侧分别作等边△APE 和△PBF ，G 为线段 EF 的中点，点 P 由点 C 移动到点 D 时，G 点移动的路 径长度为___________三、解答题（共 8 题，共 72 分）⎧x - y = 217．（本题 8 分）解方程组： ⎨ 18．（本题 8 分）已知：如图，BD ⊥AC 于点 D ，CE ⊥AB 于点 E ，AD ＝AE ，求证：BE ＝CD19．（本题 8 分）某市三景区是人们节假日游玩的热点景区，某学校对九(1)班学生“五一”小长 假随父母到这三个景区游玩的计划做了全面调查．调查分四个类别： A 、游三个景区； B 、游两 个景区；C 、游一个景区； D 、不到这三个景区游玩．现根据调查结果绘制了不完整的条形统计 图和扇形统计图，请结合图中信息解答下列问题：(1) 九(1)班共有学生______人，在扇形统计图中，表示“B 类别”的扇形的圆心角的度数为______ (2) 请将条形统计图补充完整(3) 若该校九年级有 1000 名学生，求计划“五一”小长假随父母到该景区游玩的学生多少名？20．（本题8分）运输360吨化肥，装载了6辆大卡车和3辆小汽车；运输440吨化肥，装载了8辆大卡车和2辆小汽车(1)每辆大卡车与每辆小汽车平均各装多少吨化肥？(2)现在用大卡车和小汽车一共10辆去装化肥，要求运输总量不低于300吨，则最少需要几辆大卡车？21．（本题8分）如图，⊙O△是ABC的外接圆，弧AB＝弧AC，AP是⊙O的切线，交BO的延长线于点P(1)求证：AP∥BC(2)若tan∠P＝3，求tan∠PAC的值422．（本题10分）如图，一次函数y＝kx＋b（k≠0）的图象与反比例函数ymx（m≠0）的图象交于A(－3，1)、B(1，n)两点(1)求反比例函数和一次函数的解析式(2)设直线AB与y轴交于点C，若点P在x轴上，使BP＝AC，请直接写出点P的坐标(3)点H为反比例函数第二象限内的一点，过点H作y轴的平行线交直线AB于点G．若HG＝2，求此时H的坐标(3)若点P是线段AG上一点，连接BP．若∠PBG＝1∠BAF，AB＝3，AF＝2，求（E23．本题10分）如图，射线BD是∠MBN的平分线，点A、C分别是角的两边BM、BN上两点，且AB＝BC，是线段BC上一点，线段EC的垂直平分线交射线BD于点F，连接AE交BD于点G，连接AF、EF、FC(1)求证：AF＝EF(2)求证：△AGF△∽BAFEG2GP24．（本题12分）如图，抛物线y＝ax2－(2a＋1)x＋b的图象经过(2，－1)和(－2，7)且与直线y＝kx－2k－3相交于点P(m，2m－7)(1)求抛物线的解析式(2)求直线y＝kx－2k－3与抛物线y＝ax2－(2a＋1)x＋b的对称轴的交点Q的坐标(3)在y轴上是否存在点T△，使PQT的一边中线等于该边的一半？若存在，求出点T的坐标；若不存在，请说明理由2018武汉中考数学模拟题四一、选择题(共10小题，每小题3分，共30分）1．364＝（）A．4B．±8C．8D．±42．如果分式x没有意义，那么x的取值范围是（）x1A．x≠0B．x＝0C．x≠－1D．x＝－13．下列式子计算结果为2x2的是（）A．x＋x B．x·2x C．(2x)2D．2x6÷x34．下列事件是随机事件的是（）A．从装有2个红球、2个黄球的袋中摸出3个球，至少有一个红球B．通常温度降到0℃以下，纯净的水结冰C．任意画一个三角形，其内角和是360°D．随意翻到一本书的某页，这页的页码是奇数5．运用乘法公式计算(4＋x)(x－4)的结果是（）A．x2－16B．16－x2C．x2＋16D．x2－8x＋166．已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A(0，3)、B(3，4)、C(2，2)（正方形网格中每个小正方形的边长是一个单位长度）以点B为位似中心，在网格内画出△A 1B1C1△，使A1B1C1与△ABC位似，且位似比为2∶1，点C1的坐标是（）A．(1，0)B．(1，1)C．(－3，2)D．(0，0)7．如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，这个几何体的左视图是（）A．B．C．D．8．统计学校排球队员的年龄，发现有12、13、14、15等四种年龄，统计结果如下表：年龄（岁）12131415人数（个）2468根据表中信息可以判断该排球队员的平均年龄为（）A．13B．14C．13.5D．59．观察下列各图中小圆点的摆放规律，并按这样的规律继续摆放下去，则第5个图形中小圆点的个数为（）A．50B．51C．48D．522C．m≤2D．m＞12．计算：x-1P⎩x-2y=5L L10．已知二次函数y＝x2－(m＋1)x－5m（m为常数），在－1≤x≤3的范围内至少有一个x的值使y≥2，则m的取值范围是（）A．m≤0B．0≤m≤1二、填空题（共6小题，每小题3分，共18分）11．计算：计算7－(－4)＝___________1＝___________-x-2x-211213．在－2、－1、0、1、2这五个数中任取两数m、n，求二次函数y＝(x－m)2＋n的顶点在坐标轴上的概率是___________14．为正方形ABCD内部一点，PA＝1，PD＝2，PC＝3，求阴影部分的面积SABCP＝______15．如图，将一段抛物线y＝x(x－3)（0≤x≤3）记为C1，它与x轴交于点O和点A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C2，交x轴于点A3．若直线y＝x＋m于C1、C2、C3共有3个不同的交点，则m的取值范围是___________16．如图，在平面直角坐标系第一象限有一半径为5的四分之一⊙O，且⊙O内有一定点A(2，1)、B、D为圆弧上的两个点，且∠BAD＝90°，以AB、AD为边作矩形ABCD，则AC的最小值为___________三、解答题（共8小题，共72分，应写出文字说明、证明过程或演算步骤）⎧3x+2y=317．（本题8分）解方程：⎨18．（本题8分）如图，AB∥DE，AC∥DF，点B、E、C、F在一条直线上，求证：△ABC∽△DEF19．（本题8分）某厂签订48000辆自行车的组装合同，这些自行车分为L1、L2、L3三种型号，它们的数量比例及每天能组装各种型号自行车的数量如图所示：若每天组装同一型号自行车的数量相同，根据以上信息，完成下列问题：(1)从上述统计图可知，此厂需组装L1、2、3型自行车的辆数分别是，________辆，________辆，________辆(2)若组装每辆不同型号的自行车获得的利润分别是L1：40元/辆，L2：80元/辆，L3：60元/辆，且a＝40，则这个厂每天可获利___________元(3)若组装L1型自行车160辆与组装L3型自行车120辆花的时间相同，求a（（m2-1)x y(m+1)2+21是否为一个固定的值？若是，求出其值；若不20．本题8分）为了抓住文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元(1)求购进A、B两种纪念品每件各需多少元？(2)若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，那么该商店至少要购进A种纪念品多少件？21．（本题8分）如图，⊙O是弦AB、AC、CD相交点P，弦AC、BD的延长线交于E，∠APD ＝2m°，∠PAC＝m°＋15°(1)求∠E的度数(2)连AD、BC，若BC=3，求m的值AD22．（本题10分）如图，反比例函数y=为kx与y＝mx交于A、B两点．设点A、B的坐标分别A(x1，y1)、B(x2，y2)，S＝|x1y1|，且(1)求k的值34=s-1s(2)当m变化时，代数式12是，请说理由2x ym+1(3)点C在y轴上，点D的坐标是(－1，32)．若将菱形ACOD沿x轴负方向平移m个单位，在平移过程中，若双曲线与菱形的边AD始终有交点，请直接写出m的取值范围②如图2，若AD=，作∠MDN＝2α，使点M在AC上，点N在BC的延长线上，完成图G点的直线y=-x+交于点P，C、D两点关于原点对称，DP的延长线交抛物线于点M．当23．（本题10分）如图，△ABC中，CA＝CB(1)当点D为AB上一点，∠A＝1∠MDN＝α2①如图1，若点M、N分别在AC、BC上，AD＝BD，问：DM与DN有何数量关系？证明你的结论1BD42，判断DM与DN的数量关系，并证明(2)如图3，当点D为AC上的一点，∠A＝∠BDN＝α，CN∥AB，CD＝2，AD＝1，直接写出AB·CN的积24．（本题12分）如图1，直线y＝mx＋4与x轴交于点A，与y轴交于点C，CE∥x轴交∠CAO的平分线于点E，抛物线y＝ax2－5ax＋4经过点A、C、E，与x轴交于另一点B(1)求抛物线的解析式(2)点P是线段AB上的一个动点，连CP，作∠CPF＝∠CAO，交直线BE于F．设线段PB的长为x，线段BF的长为65y，当P点运动时，求y与x的函数关系式，并写出自变量x的取值范围(3)如图2，点G的坐标为(16，0)，过A点的直线y＝kx＋3k（k＜0）交y轴于点N，与过3116k3kk的取值发生变化时，问：tan∠APM的值是否发生变化？若不变，求其值，若变化，请说明理由=22-316．22018武汉中考数学模拟题三答案一、选择题（共10小题，每小题3分，共30分）题号答案1B2C3B4D5B6B7A8B9D10A第10题选A(1)a+a+2＜1，即a＜0 2当x=a时，y最大=a2-2a-2=1a=-1，a=3(舍去）（2）a+a+2=1，即a=0 2x=a或a+2时，y最大=a2-2a-2=(a+2)2-2(a+2)-2=1无解。