华东师大版七年级下册数学:7.4.3实践与探索(3) 用二元一次方程组解决配套问题 (共18张PPT)
- 格式:ppt
- 大小:1.75 MB
- 文档页数:19

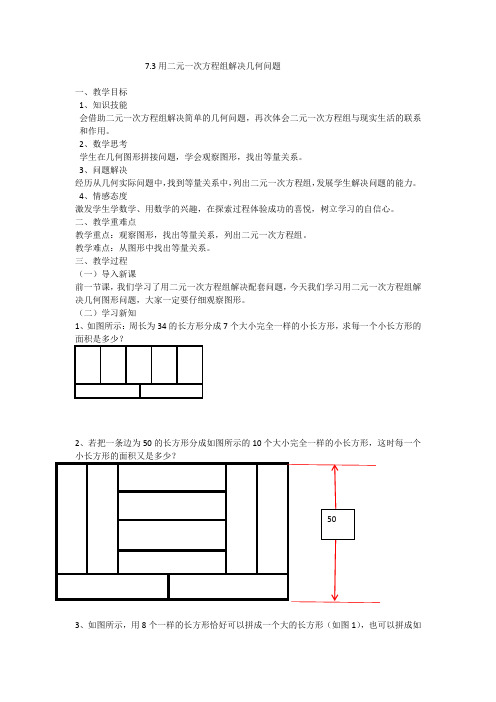
7.3用二元一次方程组解决几何问题一、教学目标1、知识技能会借助二元一次方程组解决简单的几何问题,再次体会二元一次方程组与现实生活的联系和作用。
2、数学思考学生在几何图形拼接问题,学会观察图形,找出等量关系。
3、问题解决经历从几何实际问题中,找到等量关系中,列出二元一次方程组,发展学生解决问题的能力。
4、情感态度激发学生学数学、用数学的兴趣,在探索过程体验成功的喜悦,树立学习的自信心。
二、教学重难点教学重点:观察图形,找出等量关系,列出二元一次方程组。
教学难点:从图形中找出等量关系。
三、教学过程(一)导入新课前一节课,我们学习了用二元一次方程组解决配套问题,今天我们学习用二元一次方程组解决几何图形问题,大家一定要仔细观察图形。
(二)学习新知1、如图所示:周长为34的长方形分成7个大小完全一样的小长方形,求每一个小长方形的2、若把一条边为50的长方形分成如图所示的10个大小完全一样的小长方形,这时每一个小长方形的面积又是多少?3、如图所示,用8个一样的长方形恰好可以拼成一个大的长方形(如图1),也可以拼成如图2的正方形,但中间还有一个洞,恰好是边长为2厘米的小正方形。
求每一个小长方形的长与宽是多少?图1图24、问题4:某厂家生产某种饼干包装盒的表面展开图图(如图所示),已知长方形盒子的长比宽多4厘米,求这种饼干的包装盒的体积?5问题5:某厂要制作如图所示的(1)、(2)两种无盖的长方体小盒,该厂利用边角料裁出了长方形和正方形纸片,其中长方形纸片的宽与正方形纸片的边长相等,先用70张正方形纸片和180张长方形纸片制作这两种小盒,试问可以做成(1)(2)两种小盒多少个?设计意图:让学生观察不同类型的图形,培养小组合作交流的能力,看清题意,认真观察图形,从中找见等量关系,用二元一次方程组解决问题。
(三)拓展延伸:如图所示,在矩形ABCD 中,AB=8cm,BC=6cm,点F 是AD 延长线上的一点,连接BF ,与CD 相交于点E,且三角形BEC 的面积比三角形DEF 的面积大5cm2,求DE 、CE 的长?(三)小结:回顾本节课学习的内容。


7.4 实践与探索教学目的:通过学生积极思考,探索事物之间的数量关系,构建方程模型,进一步体会方程是描绘现实世界的有效数学模型。
重点、难点1.重点:让学生实践与探索,运用二元一次方程组解决有关配套问题的应用题。
2.难点:寻找等量关系以及方程组的整数解问题。
教学媒体:PPT课件教学过程一、复习抽生回答列二元一次方程组解决实际问题的步骤是什么?关键是什么?二、新授问题1(教材P42页实践与探索中的第一个问题)。
学生观看PPT课件并与同伴讨论、交流,探索解题方法,鼓励学生多角度地思考,给予学生充分肯定和鼓励,让学生产生质问并大胆创新。
学生有困难,教师加以引导:1.通过课件直观展示问题中的实物图片;2.让学生找出本题有哪些已知量?(1)共有白卡纸20张。
(2)一张白卡纸可以做盒身2个或盒底盖3个。
(3)1个盒身与2个盒底盖配成一套。
(4)用几张白卡纸做盒身?几张白卡纸做盒底盖?3.适当地帮助学生设出未知数,并展示在图片上:若设用x张白卡纸做盒身,y张白卡纸做盒底盖。
那么可做盒身多少个?盒底盖多少个?[2x个盒身,3y个盒底盖]4.结合图片从问题中抽象出出等量关系:(1)用做盒身的白卡纸张数十用做盒底盖的自卡纸张数=20。
(2)已知(3)可知盒身的个数:盒底盖的个数=1:2。
根据题意,得=20解出这个方程组。
以上结果表明不允许剪开白卡纸,不能找到符合题意的分法。
5.如果允许剪开一张白卡纸,怎样才能既符合题意且能充分利用白卡纸呢?进一步让学生观看PPT显示的图片,添加一个条件后,鼓励学生继续讨论,并通过动手计算找到符合题意并充分利用卡纸的分法。
用8张白卡纸做盒身,可做8×2二16(个)用1l张白卡纸做盒底盖,可做3×11=33(个)将余下的l张白卡纸剪成两半,一半做盒身,另一半做盒底,一共可做17个包装盒,较充分地利用了材料。
三、巩固练习某农场300名职工耕种5l公顷土地,计划种植水稻、棉花和蔬菜,已知种植各种植物每公顷所需劳动力人数及投入的设备资金如下表:已知该农场计划在设备上投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的设备资金正好够用?先让学生自主探索,与伙伴交流。

用二元一次方程组解决配套问题1、教材分析这节课是在前面已经学习过列一元一次方程解实际问题和学习二元一次方程组的基础上进一步以“探究”的形式研究我们身边的一些现实生活问题。
学习这节课,可让学生进一步体会方程(组)是刻画现实世界的有效数学模型,它是分析和解决数学问题的一种重要的数学工具,熟练掌握列二元一次方程解决实际问题的思维方法,既是前面所学知识的延伸,又是后续学习的内容的重要预备知识,所以它在教材中处于非常重要的地位,起到了承上启下的作用。
2、教学目标(1)能正确分析实际问题中的数量关系,建立二元一次方程组模型并能解决实际问题。
(2)学会检验方程组的解是否符合题意,并正确作答。
(3)能将实际问题转化为数学问题,掌握列方程组解决实际问题的方法,进一步提高学生逻辑思维能力和分析问题、解决问题的能力。
(4)经历把实际问题抽象为数学方程组的过程,体会方程组是刻画现实世界的有效数学模型,进一步体会数学建模思想,培养学生的数学应用意识。
通过合作交流,养成学生的合作互助意识,提高数学交流和数学表达能力。
3、教学重难点重点:让学生经历和体验用方程组解决实际问题的过程,抓住实际问题的等量关系建立方程组模型。
难点:在探究过程中分析题意,由相等关系正确地建立方程组,从而把实际问题转化为数学问题即二元一次方程组。
4、教学过程设计(一)创设情景,引入新课1、复习二元一次方程组的解法——消元。
解下列方程组2、引出探究问题问题1 要用20张白卡纸做长方体包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面。
已知每张白卡纸可以做2个侧面,或者做3个底面。
如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?(二)探索分析,解决问题1、引导学生读题,寻找题中有用的数学信息1、一张方桌由1个桌面,4条桌腿组成。
如果1立方米木料可以做方桌的桌面50个或做桌腿300条,现有5立方米木料,那么用多少立方米木料做桌面、多少立方米木料做桌腿,做出的桌面和桌腿恰好配成方桌?能做成多少张方桌?2、教材44页的鸡兔同笼问题(四)课堂回顾,知识梳理1、提问:通过这节课的学习,你知道用方程组解决实际问题有哪些步骤?学生思考后回答、整理:①审清题意找相等关系;②设未知数;③列方程组;④解方程组;⑤检验并作答。

用二元一次方程组解配套问题1教学目标经历用一次方程组解决实际问题的过程,能够正确分析已知量与未知量之间的关系,能利用一次方程组解决简单的实际问题,体会用方程的思想是解决实际问题的有力工具。
感受数学来源于生活并服务于生活,培养学习数学的兴趣。
2学情分析数学来源于生活并服务于生活,生活中的许多实际问题往往可以利用方程(组)来解决,并且由此培养学生分析问题和解决问题的能力,体会方程的思想是解决实际问题的有力工具。
我校学生基础知识薄弱,因此采取形象生动的情景来帮助他们理解3重点难点教学重点:准确找出题目中的等量关系,列出方程组。
教学难点:能够用含有未知数的式子表示其他未知的量。
4教学过程4.1 第一学时教学活动活动1【讲授】一次方程组的应用复习教学过程情景引入:问题1:在“六一儿童节”中,同学们去欢乐谷游玩。
小明小红分别驾驶卡丁车从600米的卡丁车跑道出发,已知小明的驾驶速度比小红快,若两人反向行驶,则0.5分钟后两人第一次相遇;若两人同向行驶,则3分钟后两人第一次相遇。
问小明与小红驾驶的速度分别是多少?要求:(1)学生读题,找出题中隐含的等量关系:反向行驶:小明行驶的路程+小红行驶的路程=跑道长度同向行驶:小明行驶的路程-小红行驶的路程=跑道长度(2)学生完成该题的解答过程;(3)师生共同归纳列一次方程组解应用题的一般步骤。
【通过六一儿童节的契机,引入学生去欢乐谷游玩的情景,激发学生的学习兴趣。
通过分析题中的等量关系,从而解决行程问题,复习一组方程组解应用题的步骤。
】二、例题分析问题2:小张参加射击项目,已知他最后的分数是一个三位数,这个三位数十位上的数等于个位上的数与百位上的数的和;个位上的数比十位上的数小2;百位上的数与个位上的数互相调换后所得的三位数比原来的三位数大198,求这个三位数。
要求:(1)学生独立思考,找出等量关系;(2)师生交流三位数的表示方法;(3)学生完成该题的解答过程,师生归纳注意点。
华东师大版七年级下册7.4实践与探索第1课时【教学目标】1. 能够对生活中的实际问题进行数学建模,理解建模的数学思想。
2. 理解二元一次方程组在实际生活中的应用。
3. 掌握列方程组解应用题的基本思路与步骤,从而在实践中运用知识解决身边的问题。
【教学重点】列二元一次方程组解应用题的步骤。
【教学难点】在实际问题中找出等量关系。
【教学流程】一、导入新课二、实践探索<一》问题一:要用20张白卡纸做长方体的包装盒,准备将这些白卡纸分成两部分,一部分做侧面,另一部分做底面。
已知每张白卡纸可以做2个侧面,或者做3个底面。
如果1个侧面和2个底面可以做成一个包装盒,那么如何分配才能使做成的侧面和底面正好配套?引导学生阅读题目,并与同伴讨论、交流,探索解题方法,鼓励学生多角度地思考,只要学生的方法有道理,就要给予肯定和鼓励。
鼓励学生进行质问和大胆创新。
学生有困难,教师加以引导:1、本题有哪些已知量?(1)一共有白卡纸20张。
(2)一张白卡纸可以做侧面2个或底面3个。
(3)1个侧面与2个底面配成一套。
2、求什么?(1)用几张白卡纸做侧面?几张白卡纸做底面?3、若设用x 张白卡纸做侧面,y 张白卡纸做底面。
那么可做侧面 2x 个,底面 3y 个。
4、找出题目中的等量关系。
(1)用做侧面的白卡纸张数十用做底面的白卡纸张数=20(2)底面个数是侧面个数的2倍5、根据题意,可列方程组:x+y =203y=2×2x6、解方程组。
解得 7、再多动一下脑筋想想:所得结果是分数,该怎样分配这些白卡纸呢? (1)8张白卡纸做侧面,12张白卡纸做底面,则可做侧面16个,底面36 ⎪⎪⎩⎪⎪⎨⎧==7311y 748x个,共可做盒子16个,余4个底面;(2)9张白卡纸做侧面,11张白卡纸做底面,则可做侧面18个,底面33个,共可做盒子16个,余2个侧面和1个底面;(3)8张白卡纸做侧面,11张白卡纸做底面,另一张白卡纸做1个侧面和1个底面,则可做侧面17个,底面34个,正好可做盒子17个.通过分析,我们发现方案(3)较充分的利用了原材料。