Fuzzy Supervisory PI Controller Using Hierarchical Genetic Algorithms
- 格式:pdf
- 大小:176.20 KB
- 文档页数:6
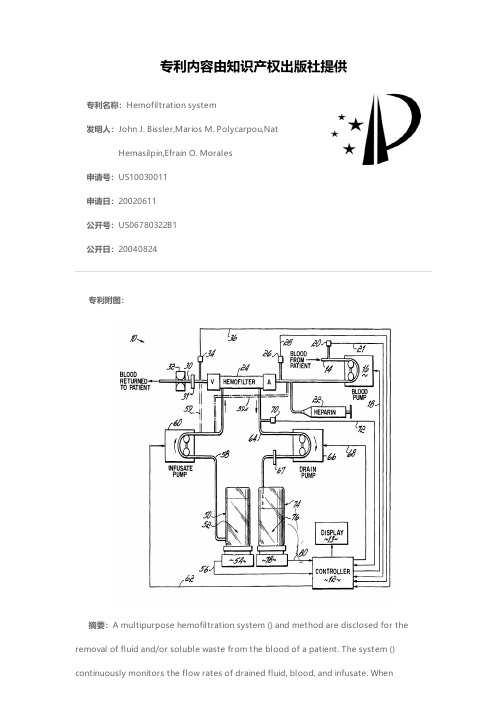
专利名称:Hemofiltration system发明人:John J. Bissler,Marios M. Polycarpou,NatHemasilpin,Efrain O. Morales申请号:US10030011申请日:20020611公开号:US06780322B1公开日:20040824专利内容由知识产权出版社提供专利附图:摘要:A multipurpose hemofiltration system () and method are disclosed for the removal of fluid and/or soluble waste from the blood of a patient. The system ()continuously monitors the flow rates of drained fluid, blood, and infusate. Whennecessary, the pumping rates of the infusate, drained fluid and blood are adjusted to remove a preselected amount of fluid from the blood in a preselected time period. A supervisory controller () can monitor patient parameters, such as heart rate () and blood pressure (), and adjust the pumping rates accordingly. The supervisory controller () uses fuzzy logic to make expert decisions, based upon a set of supervisory rules, to control each pumping rate to achieve a desired flow rate and to respond to fault conditions. An adaptive controller () corrects temporal variations in the flow rate based upon an adaptive law and a control law.申请人:CHILDREN'S HOSPITAL MEDICAL CENTER代理机构:Wood, Herron & Evans, L.L.P.更多信息请下载全文后查看。

模糊PID控制器在超临界机组协调控制系统中的应用发表时间:2016-06-20T13:41:54.423Z 来源:《电力设备》2016年第6期作者:郑伟商光刚石杨根[导读] 以辨识得到的某电厂超临界机组协调控制对象模型为基础,经过类前馈解耦。
(1.国网能源和丰煤电有限公司;2.山东电力工程咨询院有限公司;3.西安交通大学能源与动力工程学院)摘要:以辨识得到的某电厂超临界机组协调控制对象模型为基础,经过类前馈解耦,对主蒸汽压力通道、中间点温度通道进行模糊自适应PID控制系统设计。
仿真结果表明,相比传统PID控制,模糊自适应PID控制系统超调量减小,调整时间缩短,当控制量发生扰动时,系统表现出更好的鲁棒性。
关键词:协调控制;模糊控制;前馈解耦Application of fuzzy PID Controller in coordinated control object of supercritical unitWei Zheng1 Guanggang Shang2 Yanggen Shi3(1. Stste Grid Energy Hefeng coal and electricity Co.Ltd.2.Shandong Electric Power Engineering Consulting Institute Corr, Ltd. 3. College of energy and power engineering,Xi’an Jiaotong University)ABSTRACT:Based on the feedforward compensation decoupled model of coordinated control object, fuzzy adaptive PID controller is designed for the main steam pressure channel and the middle point temperature channel of the coordinated control object. The simulation results show that, using the fuzzy PID controller,the overshoot of controlled variable decreases and the adjustment timereducesin response to a step change compared with traditional PID controller. And the control system of fuzzy adaptive PID controllershows better adaptive performance when controlling variable changes.Keywords: Coordinated control;Fuzzy control; Feedforward Decouple超临界机组目前应用最广泛的仍为PID控制器,同时为保证控制的及时有效性,各电厂普遍采用前馈控制技术[1]。

Fuzzy Systems and Control Fuzzy systems and control are an essential part of modern engineering and technology. They are used in a wide range of applications, from controlling industrial processes to managing traffic flow in cities. The concept of fuzzylogic is based on the idea that many real-world problems are too complex to be described by precise mathematical models. Instead, they require a more flexible approach that can deal with uncertainty and imprecision.One of the key advantages of fuzzy systems is their ability to handle uncertainty. In traditional control systems, inputs and outputs are defined by precise mathematical models. However, in the real world, there are often many factors that can affect these inputs and outputs, such as noise, variability, and measurement errors. Fuzzy systems are designed to cope with these uncertainties by using a range of linguistic variables to describe the system's behavior. This allows them to produce more robust and reliable control outputs, even in the face of unpredictable events.Another important advantage of fuzzy systems is their ability to deal with imprecision. In many situations, it is difficult to define precise rules for how a system should behave. For example, in a traffic management system, it is notalways clear how drivers will respond to changing road conditions. Fuzzy systems allow engineers to define rules in a more flexible way, using linguistic variables such as "slow," "moderate," and "fast." This allows the system to adapt to changing conditions and produce more accurate and responsive control outputs.Fuzzy systems are also highly adaptable and can be used in a wide range of applications. They are used in industrial automation, robotics, and process control, as well as in more specialized areas such as medical diagnosis and financial forecasting. This versatility is due to the fact that fuzzy systems can be easily customized to suit different requirements. They can be designed tohandle different types of inputs, such as temperature, pressure, or flow rate, and can be programmed to produce different types of outputs, such as motor control signals or alarm signals.Despite their many advantages, fuzzy systems are not without their limitations. One of the main challenges is designing the system's rules and membershipfunctions. These must be carefully chosen to ensure that the system produces accurate and reliable outputs. This can be a time-consuming and complex process, requiring a deep understanding of the system's behavior and the factors that affect it. In addition, fuzzy systems can be difficult to debug and maintain, particularly if the rules and membership functions are poorly designed.Another limitation of fuzzy systems is their reliance on human expertise. In order to design an effective fuzzy system, engineers must have a deep understanding of the system they are working with and the factors that affect it. This can be a significant challenge, particularly in complex systems where there are many interacting variables. In addition, the process of designing a fuzzy system can be highly subjective, with different engineers producing different results based on their own expertise and experience.In conclusion, fuzzy systems and control are an important part of modern engineering and technology. They offer a flexible and adaptable approach to control and are used in a wide range of applications. However, they also present significant challenges, particularly in terms of designing the system's rules and membership functions and relying on human expertise. Despite these limitations, fuzzy systems are likely to play an increasingly important role in the future of engineering and technology, as they offer a powerful tool for dealing with uncertainty and imprecision in complex systems.。

一类时滞系统的fuzzy-pi-smith控制方法
Fuzzy-PI-Smith控制方法是一种应用于时滞系统的控制器设计方法。
它通过基于聚类原理的模糊控制理论,将模糊系统控制与PID传
统控制进行整合。
它由三个部分组成:fuzzy模块、PI模块和变频器
模块。
fuzzy模块使用聚类函数法,将模糊规则转换为当前数学模型;
PI模块能够控制系统的输入和输出;变频器模块可以改变控制器的参数。
Fuzzy-PI-Smith控制方法的优点在于它的模糊系统有效地处理了
时滞系统中的非线性,减少了控制器的调节精度,提高了系统的可靠
性和稳定性;PI模块能够控制系统的输入和输出,调节系统的输入量
以实现动态精度;变频器模块可以改变控制器参数来控制系统收敛性、稳定性和鲁棒性。
Fuzzy-PI-Smith控制方法也有一些缺点,尤其是其调参复杂性问题。
此外,fuzzy模块也有许多参数,这些参数是需要经过大量试验才
能获得的,而且很难获取合理的参数。
因此,一旦变量参数发生变化,fuzzy-pi-smith控制器的性能也会受到影响。
总而言之,Fuzzy-PI-Smith控制算法在控制时滞系统的方面具有
优秀的表现,但是在某些情况下它也有一些缺点。

第33卷第5期2004年10月 信息与控制Information and ControlVol.33,No.5 Oct.,2004 文章编号:100220411(2004)0520637204一种新型模糊非线性PID控制器李祖欣,蒋云良(湖州师范学院信息工程学院,浙江湖州 313000)摘 要:采用一维输入一维输出的模糊映射关系与传统PID控制器相级联的方式,构成一个模糊非线性PID控制器以提高现有PID控制器的性能.一维模糊控制器无需选择与调整量化因子和比例因子,采用五条规则,易于实现.数值仿真和误差泛函积分评价指标表明,所提出的模糊非线性PID控制器比现有控制器具有更好的动静态性能.Ξ关键词:模糊控制;PID控制;非线性PID控制;非线性控制中图分类号:TP273 文献标识码:BA N e w Fuzzy Nonlinear PID ControllerL I Zu2xin,J IAN G Yun2liang(School of Inf ormation and Engi neeri ng,Huz hou Teachers College,Huz hou 313000,Chi na) Abstract:A new fuzzy nonlinear PID controller is proposed,which adopts the fuzzy mapping relations between one2dimensional input and one2dimensional output and the cascaded mode of traditional PID controller.One2dimen2 sional fuzzy controller,which has no scaling factors to adjust and only needs simple five rules,is easy to be realized.Simulation results and evaluation criteria for function behaviors of the controller show that the proposed PID con2 troller has better performance than the conventional PID and other nonlinear PID controllers.K eyw ords:fuzzy control;PID control;nonlinear PID control;nonlinear control1 引言(Introduction)PID控制由于结构简单、工作稳定、鲁棒性好等因素在当今的工业过程控制中仍占有主导地位[1].常规PID控制中的比例、积分和微分三种控制分别独立发挥作用,三个参数对应的控制效果意义明确[2],这种简明的控制分量独立整定效果对于工程应用操作起来是十分方便的.但传统PID控制对于跟踪设定值与抑制扰动或系统参数变化等方面,通常采取折衷的办法,使系统不能获得较佳的控制效果.传统PID存在上述问题本质上是PID控制中P、I、D的线性组合及系统特性变化与控制量之间的线性映射关系造成的. 为了突破PID控制的线性控制,近年来提出了各种非线性控制器[3,4],以提高系统的控制性能.模糊控制器输入输出本身存在着变增益的非线性关系,可以解决动态时的快速性和稳定性问题,它因而成为智能自动化控制研究中最为活跃而富有成果的一个领域.其中,模糊PID控制技术扮演了十分重要的角色,并且仍将成为未来研究与应用的重点技术之一[5]. 针对模糊控制和PID控制的各自优点,也出现了将PID控制器与模糊控制相结合的各种复合控制[6].从模糊控制器的结构上分析,常见的模糊控制器一般分为二维、三维模糊控制器,但随着输入变量的增加,任何模糊控制系统将遭受由规则爆炸引起的维数灾难[7],故二维模糊控制器应用较普遍.为了克服二维或三维模糊控制器的控制分量合成、输入耦合影响和增益相关等功能缺陷,出现了基于“1D-3D”映射关系的最佳一维模糊控制器[8,9]. 本文将基于“1D-1D”映射关系的一维模糊控制器产生的非线性增益关系与PID控制器相级联构成了一个模糊非线性PID控制器.一维模糊控制器无需选择与调整量化因子和比例因子,采用五条规则,实现了输入与输出的非线性增益关系.该非线性控制器设计简单,利用原有的PID控制参数,易于实现.数值仿真表明,所设计的模糊非线性PIDΞ收稿日期:2004-02-10 基金项目:浙江省自然科学基金资助项目(M603169)控制器(FN PID)与文献[4]的非线性PID控制(N PID)相比,无需构造合适的非线性函数和选择两个附加参数,可大大降低阶跃响应上升时间,有良好的跟踪设定值能力.2 传统PID控制器(Conventional PID con2 troller)连续形式的PID控制器算式为:u(t)=K P e(t)+1T i∫te(t)d t+T dd e(t)d t(1)相应的离散化的控制算法为:u(t)=K P e(k)+TT i∑kj=0e(j) +T dT[e(k)-e(k-1)](2) 式中u(k)是第k次采样时刻计算机的输出, K P为比例系数,T、T i、T d分别为采样周期、积分时间常数和微分时间常数. 根据不同对象特点和控制要求,PID又可分为PI、PD、PID、增量PID、积分分离PID以及带各种滤波器的PID控制器.对于不同的被控对象只要适当地整定PID参数,就可以获得满意的控制效果,实际上它是对比例、积分和微分三部分控制作用的折衷.PID参数的整定存在着许多经验公式和整定方法,如Ziegler2Nichols方法、Cohen2Coon方法、Chien2 Hrones2Reswick方法、IMC方法、IST2E方法、极点配置方法、幅值相位裕量方法等等.确定后不变的PID参数在性能上很难同时满足跟踪设定值、抑制扰动或者变换模型参数等方面的要求.因而传统PID控制的线性关系常常引起系统快速性和超调量之间的矛盾.3 模糊非线性PID控制器(Fuzzy nonlinear PID controller)3.1 基于“1D-1D”映射关系的一维模糊控制器 当文献[8]的基于“1D-3D”映射关系的最佳一维模糊控制器的三个互不线性相关的Fuzzy P的论域和规则库取相同时,该形式即简化为“1D-1D”映射关系的模糊控制器.一维模糊控制器没有多维模糊控制器的功能缺陷[9],但使输入与输出呈现一种非线性增益关系.本文提出的基于“1D-1D”映射关系的一维模糊控制器的输入输出隶属度函数和控制规则表如图1、表1所示.其控制规则为:else[if E is A i then U is B i].模糊控制器的解模糊运算由下式确定:u f(k)=∑5j=0(A j(E(k))・u j)∑5j=0A j(E(k))(3)式中u j满足B j(u j)=1.为简化分析,将输入的论域归一化处理,当系统处于起动阶段时,考虑如下输入区域:E∈[0.75,1],此时激活两条规则:if E is PM then U is M;if E is PB then U is B.由式(3)得: u f=b1A1(E(PM))+b2A2(E(PB))A1(E(PM))+A2(E(PB))(4)此处E的隶属度函数采用三角形、均匀分布、全交叠的隶属度函数,故上式可简化为:u f=b1a+b2(1-a)(5)式中,系数a为输入模糊子集PM的隶属度函数,其表达式为:a=A1(E(PM))=max minE0.5,1-E0.5,(6)同理,当系统进入稳态阶段时,考虑如下输入区域: E∈[0,0.25],由式(3)得:u f=b1a+(1-a)(7)从式(5)、(6)和(7)中很容易看出,u f的值域为[1, b2],当起动时,u f有较大值,当进入稳态时,u f变小,最终u f=1,它们的输入和输出呈现了一种非线性关系,但正是这种非线性关系使得系统的性能大大提高.图1 模糊集的输入输出隶属度函数Fig.1 Input and output membership functions of fuzzy sets表1 模糊控制器规则表Tab.1 Fuzzy controllerπs rule baseE NB N M ZE PM PBU B M S M B836信 息 与 控 制33卷 3.2 模糊非线性PID 控制器 将上述的一维模糊控制器和PID 控制器相级联即成为模糊非线性PID 控制器(FN PID ),如图2所示.一维模糊控制器输出的结果是由误差控制的单控制分量,即为模糊比例控制分量,它由简单的五条规则组成,无需调整量化因子和比例因子,容易实现.由图2可知:u p (k )=e (k )・u f (k )(8) 由于u p 与e 的非线性关系,使得PID 控制器各等效增益也呈非线性.在系统起动时,系统输出趋向稳态值的速度越快越好,即应尽快消除偏差,加大偏差的权值.因此,非线性的作用使得PID 有更大的误差权值,使得系统有更好的快速性,在进入稳态时,Fuzzy P 的非线性增益为1,从而保留稳态时PID 控制的优点.因此它比传统PID 具有更好的性能,可以兼顾快速性和稳态精度的要求.另外在FN 2PID 中,传统PID 控制中原有的增益参数与输入变量关系、控制分量和控制效果的物理意义在广义上仍有保留,这对于熟悉传统PID 控制的工程师来说是十分重要的.图2 模糊非线性控制系统框图Fig.2 Fuzzy nonlinear control system4 仿真分析(Simulation analysis)本文分别对传统PID 、文献[4]的N PID 和本文的FN PID 进行了数值仿真,被控对象和已有参数均取自文献[4],考虑计算机采样用零阶保持器,其广义被控对象为:G (z )=(b 0+b 1z -1)z -11+a 1z -1+a 2z -2(9)相应的差分方程为:y (k )=-a 1y (k -1)-a 2y (k -2)+b 0u (k -1)+b 1u (k -2)(10)式中,k 为采样时间序列;y 为输出量;u 为控制变量;模型参数为:a 1=-1.8165,a 2=0.8187,b 0=0.0012,b 1=0.0011.传统PID 控制器参数采用Ziegler 2Nichols 规则整定后,通过以Neilder 和Mead 提出的柔性多面体搜索算法(单纯形寻优法)得到.在上述条件下,PID 、N PID 和FN PID 的阶跃响应如图3所示.表2是基于误差泛函积分评价指标的性能数据比较,计算时间为2s .误差泛函积分评价指标是以控制系统的瞬时误差函数e (t )为泛函的积分评价,包括IE 、ISE 、ISTE 、IAE 、ITAE 等.对抑制大误差,ISE 比IAE 好;而抑制小的误差,IAE 比ISE 好;ITAE 能较好地抑制长时间存在的误差[2].因此,ISE 指标对应的系统响应,其最大动态偏差较小,调节时间较长,与ITAE 指标对应的系统响应调节时间最短. 从图3和表2中可以看出,模糊非线性PID 控制的阶跃响应速度明显优于传统PID 、N PID 的响应速度,这种优良动态控制特性得益于Fuzzy P 的非线性增益的作用,当系统在初始状态时,非线性增益较大,当达到稳态时,一维Fuzzy P 的增益又恢复为1,即只有固定增益的传统PID 控制器起作用了.因此,它具有比PID 控制更优的系统性能.图3 PID 、NPID 和FNPID 阶跃响应Fig.3 Step 2responses of PID ,NPID and FNPID表2 PID 、NPID 和FNPID 性能比较Tab.2 Performance comparison of PID ,NPID and FNPID类型ISE ISTE IAE ITAE PID 0.09570.00070.15340.0185NPID 0.08000.00040.13110.0145FNPID0.06430.00020.10790.01105 结语(Conclusion)本文针对传统PID 控制不能同时获得动静态性能的弱点和文献[4]的N PID 控制需构造合适的非线性函数及调整两个附加参数的问题,利用一维Fuzzy P 的模糊非线性关系与传统PID 相级联从而获得FN PID 控制器.它设计简单,无需调整其它附加参数,而使控制系统具有了更优的系统性能.参 考 文 献(R eferences)[1] Chen G.Conventional and fuzzy control PID controller :anoverview [J ].International Journal of Intelligent Control and9365期 李祖欣等:一种新型模糊非线性PID 控制器Systems ,1996,1(2):235~246.[2] 金以慧.过程控制[M ].北京:清华大学出版社,1993.[3] Xu Y ,Hollerbach J M ,Ma D.A nonlinear PD controller forforce and contact transient control [J ].IEEE Control System Magazine ,1995,15(1):15~21.[4] 苏玉鑫,段宝岩.一种新型非线性PID 控制器[J ].控制与决策2003,18(1):126~128.[5] 胡包钢,应 浩.模糊PID 控制技术研究发展回顾及其面临的若干重要问题[J ].自动化学报,2001,27(4):567~584.[6] Leonid R ,Omar G ,Anna B.PID plus fuzzy controller structuresas a design base for industrial applications [J ].Engineering Appli 2cations of Artificial Intelligence ,2000,13(4):419~430.[7] K osko B.FuzzyEngineering [M ].New Jersey :Prentice Hall ,1997.[8] Mann G K I ,Hu B G ,G osine R G.Analysis of direct actionfuzzy PID controller structures [J ].IEEE Transactions on Sys 2tem ,Man ,and Cybernetics -Part B :Cybernetics ,1999,29(3):371~388.[9] 胡包钢,Mann C K I ,G osine R G.关于模糊PID 控制器推理机维数的研究[J ].自动化学报,1998,24(5):608~615.作者简介李祖欣(1972-),男,硕士,讲师.研究领域为模糊控制及单片机技术.46信 息 与 控 制33卷 。

典型模糊控制器(Fuzzy controller)的设计任璐风【期刊名称】《科技资讯》【年(卷),期】2010(000)026【摘要】现代化的安全生产中控制理论在电气上的运用非常广泛,但现实环境的变化无常对控制器提出更高的要求,因而有了模糊控制器的研究和设计,它主要是把一个或多个模糊的概念通过控制转换变成一个规则的可控输出.【总页数】1页(P11-11)【作者】任璐风【作者单位】临汾市安全生产教育培训中心,山西临汾,041000【正文语种】中文【中图分类】X9【相关文献】parative Analysis between Conventional PI, Fuzzy Logic and Artificial Neural Network Based Speed Controllers of Induction Motor with Considering Core Loss and Stray Load Loss [J],Md.;Rifat;Hazari;Effat;Jahan;Mohammad;Abdul;Mannan;Junji;Tamura;2.Parallel Fuzzy P+Fuzzy I+Fuzzy D Controller: Design and Performance Evaluation [J], Vineet Kumar;A.P. Mittal3.Stability of Nonlinear Systems Using Optimal Fuzzy Controllers and Its Simulation by Java Programming [J], Mohammad Javad Mahmoodabadi; Saideh Arabani Mostaghim4.Stability of Nonlinear Systems Using Optimal Fuzzy Controllers and Its Simulation by Java Programming [J], Mohammad Javad Mahmoodabadi; Saideh Arabani Mostaghim5.Controlling Speed of DC Motor with Fuzzy Controller in Comparison with ANFIS Controller [J], Aisha Jilani;Sadia Murawwat;Syed Omar Jilani因版权原因,仅展示原文概要,查看原文内容请购买。
调用fuzzy工具箱,生成的是一个.fis的文件,文件名就是你在工具箱里边定义的名字,如图中的4位置。
通过调用file—import—from file可以导入使用文本编辑其编辑好的fis文件,进行修改。
可以把编辑好的模糊推理器导出到文件中。
File—export如图中1位置,当选中一个模块的时候,相应的模块边框会变色。
双击就可以对他进行编辑,输入的模糊话,输出(图总位置3)的去模糊。
双击图中2位置的模块添加相应的模糊推理规则,对应生成的fis文件当中的[rules]下边的东东。
图中位置5和位置6对应的地方的内容基本不用变,目前模糊推理一般都用的这种方法。
图中位置7的位置是选中上边的模块的时候,相应的信息,可以修改名字,但不能编辑其他的内容。
这个图是模糊推理输入输出成员函数(membership function)的编辑其,选中位置1的其中一个,就可以编辑对应的隶属度函数。
Add MFS 是成组添加隶属度函数。
这种方式添加的时候,隶属度函数的类型是一样的,比如都用三角函数,或都用高斯函数。
用三角的多。
Add custom mf这个是单独添加一个隶属度函数。
其中涉及到得几个变量是:模糊语言变量名称。
如图总共的mf1,mf2,对应实际用的NB NM 之类的。
还有就是隶属度函数类型。
再一个就是隶属函数对应的几个端点。
高斯和三角都有三个,s型函数和z型函数有两个。
当然添加隶属度函数的时候,可以先确定形状,选用什么类型的函数,然后是用几个,完了先粗略的添加进来。
之后可以在上图位置2对应要修改的隶属函数,选中以后,移动各个小方块,再细改。
注意位置2右上角的,那个是函数曲线显示的点数,显示的越多,越精细,但是可能就越耗cpu。
我见过的一般都用三角,计算简单。
顶多最左边用z型函数,最右边用s函数。
中间用一个高斯。
输入输出隶属度函数确定后,完了就是编辑模糊规则位置1为添加好的规则。
位置2为输入组合逻辑,mf1,mf2对应各个输入的模糊语言变量,具体看实际是定的名字。
Fuzzy Supervisory PI Controller Using HierarchicalGenetic AlgorithmsKiatkajohn Worapradya and Suvalai PratishthanandaDepartment of Electrical Engineering,Faculty of EngineeringChulalongkorn University,Bangkok10330Thailande-mail:john@control.ee.eng.chula.ac.th,suvalai@ee.eng.chula.ac.thAbstractThis paper presents a fuzzy supervisory PI controller using a Hierarchical Genetic Algorithm(HGA).HGA which is an optimization algorithm is used to define the optimal number and shape of membership functions, and fuzzy rules.The fuzzy supervisory PI controller is designed and simulated on a heat exchanger sys-tem.Sum of square error and sum of absolute error are used as objective functions.Simulation results are compared with the PI controller using˚A str¨o m and H¨a gglund tuning.Improved performances can be noticed.1IntroductionThe general structure of fuzzy systems consists of three principle components:a fuzzifier unit which is a process to transform input signals into fuzzy sets,an inference engine which is a decision process to approx-imate reasoning with fuzzy rule bases,and,finally,a defuzzifier unit which transforms the fuzzy sets into output signals.In order to work efficiently,this struc-ture has to use optimal membership functions and rule bases.However,there are no exact methods to con-struct them.Therefore,the conventional approaches usually base on the operators’skills,experience,and trial-and-error method.To solve this problem,many researchers designed optimal membership functions and rule bases by using different methods such as neural network[2],cluster-ing[3,4],gradient method[5],simulated annealing [6,9],and genetic algorithms[7,8,9,10].Among these methods,the genetic algorithms method is the most in-teresting.For examples,it dose not use derivative in-formation,it searches from a population of points(not a single point),and it is a powerful tool for solving a multi-objectives function problem.Although genetic algorithms can search the optimal shape of membership functions and optimal rules,it cannotfind the proper number of membership func-tions and rules.Therefore,Man,Tang,Kwong and Liu [1]suggested a Hierarchical Genetic Algorithms which canfind the optimal number and shape of membership functions,and rules.In this paper,we propose the design of fuzzy supervisory system which is used for supervising the PI controller.We use the HGA for designing opti-mal membership functions and rules.The obtained fuzzy supervisory PI controller is simulated on the heat exchanger.To demonstrate the better performance,we compare the designed responses with the response of PI controller tuning via˚A str¨o m and H¨a gglund method.2Hierarchical Genetic AlgorithmsHGA is a type of the genetic algorithms,introduced by Man,Tang,Kwong and Liu[1].Its structure is moreflexible than the conventional genetic algorithms (GAs)while it still has important genetic operations. The only difference between HGA and GAs is the chro-mosome form.2.1Hierarchical Chromosome Formulation Concept of hierarchical chromosome is regarded as DNA in a biological chromosome.DNA consists of two types of genes which are structure genes and regulatory genes.The structure genes contain the genetic infor-mation and the regulatory genes control coding of the structural genes.Similarly,a hierarchical chromosome can be classified into two different types,i.e.,para-metric genes and control genes.The parametric genes, which contain parameter values,are analogous to the structure genes.The activation of the parametric genes is governed by the value of the control genes which is analogous to regulatory sequences.In Figure1,a three levels gene structure is illustrated. The parameter genes are governed by thefirst level control genes which are governed by the second level control genes,respectively.The value0or1is used to define the activation of the parametric genes,an integer1is assigned for each control gene that is being ignited,where0is for turning off.When the value2nd levelcontrol gene 1st level control geneparametric geneFigure 1:General form of a hierarchical chromosome of control gene is 1,the associated parametric genescorresponding to that control gene are activated and they are inactivated when the value of control gene is 0.2.2Genetic OperationsGenetic operation of HGA consists of three pro-cesses which are selection,crossover,and mutation.Crossover and mutation are operated independently between control genes and parametric genes.A muta-tion method depends on the coding of a chromosome.3HGA for fuzzy system3.1Coding of fuzzy systemGenerally,problems solved by GAs,the variables are coded to chromosome form.Similarly,in HGA the parameters of membership functions and fuzzy rules are coded to hierarchical chromosome form which is different between membership chromosomes and fuzzy rule chromosomes.The HGA chromosome consists of the usual two types of genes,the control genes (z c )and parametric genes (z p ).The control genes,in the form of bits,deter-mine the membership function activation,whereas the parametric genes are in the form of real numbers to represent the membership functions.The HGA coding is shown in Figure 2.With the two input fuzzy sets of error signal (e )and error rate (∆e )and the output fuzzy set of ∆u ,we can define the parametric genes of the membership chromosome as z p={αE1a ,αE 1b ,αE 1c ,...,αE ma ,αE mb ,αE mc ,β∆E1a ,β∆E 1b ,β∆E 1c ,...,β∆E na ,β∆E nb ,β∆E nc ,γ∆U1a ,γ∆U 1b ,γ∆U 1c ,...,γ∆U pa ,γ∆U pb ,γ∆U pc }(1)where m ,n ,and p are the maximum allowable numbers of the fuzzy subset of e ,∆e ,and ∆u ,respectively,αEia ,αE ib ,αE ic define the input membership functionof the i th fuzzy subset of e ,β∆Eja ,β∆E jb ,β∆E jc define the input membership function of the j th fuzzy subset1a1cnanbnccontrol genes (z )parameter genes (z ) pnanbnc2a2b2c1b1c1a1bFigure 2:A membership chromosomeof ∆e ,γ∆U ka,γ∆U kb ,γ∆Ukc define the input membership function of the k th fuzzy subset of ∆uTo code a fuzzy rule into a fuzzy rule chromosome,the number of rules depend on the number of fuzzy subset of e and ∆e which is corresponding to the number of actived control genes.Therefore,the fuzzy rule base should be classified,corresponding to the number of actived control genes.In order to make it easy,the fuzzy rule base should be coded in matrix form which is similar to a fuzzy rule table as shown in Table 1.Table 1:The Rule Base in Tabular FormD 1D 2···D j ···D xE 1U 1U 2···U j E 2U 2U 3···U j......E i ···U k ···......E wU i···U yWe code the fuzzy rule table in Table 1into the fuzzy rule chromosome H (w,x,y )which is formulated in the form of an integer matrixH (w,x,y )=⎡⎢⎣h 1,1···h 1,j .........h i,1···h i,j⎤⎥⎦(2)where h i,j ∈[1,y ]and ∀i ≤w,j ≤x and the i −jelement implies the following rule:R ij :If e is E i and ∆e is D j then ∆u is U kwhere E i ,D j and U k are the linguistic names which characterize the fuzzy subsets of e ,∆e ,and ∆u ,re-spectively.3.2Genetic Operations for fuzzy systemDue to the fact that the membership chromosomes con-sist of control genes and parametric genes,each type of gene has to use different genetic operations.For the crossover operation,a one-point crossover is appliedseparately for both the control and parametric genes of membership chromosomes within certain operation rates.The fuzzy rule chromosome has no crossover operation because there is only one fuzzy rule chromo-some per one matrix dimension.Bit mutation is applied for the control gene of the mem-bership chromosome.Each bit of the control gene is changed from1to0or from0to1if a probability test is satisfied(a big probability).As for the para-metric genes,which are real-number represented,ran-dom mutation is applied.The random mutation is presented byg=g+ψ(µ,σ)(3) where g is the real value gene,ψis a random function which may be Gaussian or normally distributed,µand σare the mean and variance related with the random function,respectively.To mutate the fuzzy rule chromosome,a special muta-tion operation is applied.It is called delta operation which alters each element in the fuzzy rule chromosome as follows:h i,j=h i+∆i,j+∆j(4) where∆i and∆j have an equal chance to be1or-1, with a small probability.4Design example:The fuzzysupervisory PI controller ofa heat exchangerFigure3:The fuzzy supervisory PI controllerIn this section,we present an example of the fuzzy supervisory control system design using HGA which is discussed in last section.This fuzzy supervisory system,as a second level controller,is used for super-vising a PI controller of heat exchanger.The fuzzy supervisory control system is shown in Figure3.The membership functionsand fuzzy rules,are defined by HGA and this fuzzy structure is used for K p and K I parameters tuning of the PI controller.The tuning occurs when disturbance is applied or the set point is changed.ShutterTo Ti , Fi InletFigure4:Heat exchanger system4.1Characteristic and mathematical model ofa heat exchangerA heat exchanger is shown in Figure4.A constant velocity blower draws the air into the tube and the air volume is controlled by a shutter.The air which passes through the tube is heated by a heater.The heater power is applied by thyrister as the actuator corresponding to control signal.The heated airflows to the end of the tube and is detected by the temperature sensor.The detected temperature is transformed into the voltage by bridge circuit and transmitted to control the system.For linearized model of the heat exchanger,which is a first order plus time delay system,Wang[7]as:G(s)=10e−0.13s0.33s+1(5)where the input is the voltage supplied to heater and the output is the temperature measured by the detector.4.2SimulationsTo simulate,we consider the set point change problem. The temperature at the detecting point is required to be increased to60◦C from an initial value of20◦C at 6th second and then decreased back to20◦C at12th second.The parameters of optimization are as follows:•The parameters of the fuzzy system.–e∈[−50,50]and∆e∈[−5000,5000].–K P∈[0.06,0.3]and K I∈[0.2,0.5].–Minimum inference engine.–Center average defuzzifier.•The parameters of HGA.–The maximum number of the input fuzzysubsets of e and∆e=5and the number ofthe output fuzzy subsets of K P and K I=2(m=n=5and p=q=2).–The number of generations=20.–The other parameters are shown in Table2.Table 2:The parameters of HGAMembership Chromosome Fuzzy Rule Control Parameter ChromosomeGenes Genes Representation Binary RealInteger Population Size 202016No.of Offspring 221Crossover One point One point -Crossover Crossover-Crossover Rate 0.90.9-Mutation Bit Random Delta Mutation Mutation Operation Mutation Rate 0.010.010.01SelectionRoulatte Wheel SelectionBase on the no.of active fuzzy subsetsTo define the fitness functions (F ),the fitness functions are selected as inverse proportion to the objective func-tion (J ).This process will yield a high sentivity string selection,as suggested by Wang [7].In this paper,two different objective functions and fitness functions are used.These objective functions are standard for dis-turbance rejection and set point following problems.•Case I :Sum of squared error objective function is shown as formula (6)and the fitness function is shown as formula (7).J 1=k i =1e 2i(6)F 1=106J(7)•Case II :Sum of absolute error objective func-tion is shown as formula (8)and the fitness func-tion is shown as formula (9).J 2=k i =1|e i |(8)F 2=105J(9)where e is error.4.3Simulation resultsIn Case I,the largest fitness function gives the fuzzy structure as:the optimal number of the input fuzzy subsets of both e and ∆e are 4.The shape of them are shown in Figure 5and Figure 6,respectively.The optimal number of output fuzzy subsets of both K P and K I are 2and the shape of them are shown in Figure 7(a)and 7(b),respectively.The optimal fuzzy rule bases of K P and K I are shown in Table 3and 4,respectively.In case II,The optimal number of the input fuzzy sub-sets of e and ∆e are 3and 2,and the shape of them-500-10-20-30-401020304050E1E2E3E41Figure 5:Membership function of e :Case I0-1000-2000-3000-4000-500010002000300040005000D1D2D3D41Figure 6:Membership function of ∆e :Case I0.30.30.40.20.20.10.06U1U2V1(b)1V2(a)0.5Figure 7:(a)Membership function of K P (b)Member-ship function of K I :Case ITable 3:Optimal rule table for K P :Case I∆e D 1D 2D 3D 4E 1U 2U 1U 1U 1eE 2U 2U 2U 2U 2E 3U 2U 1U 1U 1E 4U 2U 1U 2U 1Table 4:Optimal rule table for K I :Case I∆e D 1D 2D 3D 4E 1V 2V 1V 1V 1eE 2V 2V 2V 2V 2E 3V 2V 1V 1V 1E 4V 2V 2V 2V 2are shown in Figure 8and 9,respectively.The opti-mal number of output subsets of both K P and K I are 2and the shape of them are shown in Figure 10(a)and 10(b),respectively.The corresponding rule tables are shown in Table 5(a)and 5(b),respectively.The best objective values in each generations are ploted in Figure 11.These optimal fuzzy supervisory systems are simulated on the heat exchanger.Simulation results,which are compared with the PI controller using ˚A str¨o m and H¨a gglund tuning,are shown in Figure 12and 13.Case I has the shortest rise time,while Case II has the shortest settling time and the smallest overshoot.-500-10-20-30-401020304050E1E2E3Figure 8:Membership function of e :Case II0-1000-2000-3000-4000-500010002000300040005000D1D21Figure 9:Membership function of ∆e :Case II0.30.40.20.50.20.10.060.3U1U2V1V21(a)(b)Figure 10:(a)Membership function of K P (b)Member-ship function of K I :Case IITable 5:(a)Optimal rule table for K I (b)Optimalrule table for K I :Case II (a)(b)∆e D 1D 2E 1U 1U 2e E 2U 2U 1E 3U 1U 2∆e D 1D 2E 1V 1V 1e E 2V 2V 2E 3V 1V 1Case I uses almost the same control signal as the ˚A str¨o m-H¨a gglund while Case II uses the smallest.5ConclusionsIn this paper,the design of the fuzzy supervisory PI controller by HGA is proposed.HGA is used to search for the optimal number and shape of member-ship functions,and fuzzy rules.The fuzzy supervisory PI controller for heat exchanger is designed.Sum of squared error and sum of absolute error are used as objective functions and the set-point following prob-lem is considered.After optimization processes and simulation,the fuzzy subsets are reduced.The close-loop performance is better than the ˚A str¨o m-H¨a gglund.However,selection of the objective functions depends on applications.Figure 11:Thebest objective values in each generations[3]Hong T.P.,and C.Y.Lee,Induction of fuzzy rulesand membership functions from training examples, Fuzzy Sets and Systems,pp.33–47,1996.[4]Klawonn F.,and R.Kruse,Constructing a fuzzycontroller from data,Fuzzy Sets and Systems,pp.177–193,1997.[5]Araki S.,H.Nomura,I.Hayashi,and N.Wakami,Self-generating method of fuzzy inference rules,Int.Fuzzy Engineering Sysposium,pp.1047–1058,1992.[6]Huyghe E.,and Y.Hamam,Simulated annealing forfuzzy controller optimization:Principles and appli-cations,IEEE Int.Conf.System,Man and Cyber-netics,Vol.5,No.1,pp.4509–4514,1995.[7]Wang P.,and D.P.Kwok,Optimal fuzzy PID con-trol based on genetic algorithm,Proc.of the IEEE, pp.977–981,1992.[8]Karr C.L.,and E.J.Gentry,Fuzzy Control of pHUsing Genetic Algorithms,IEEE Trans.Fuzzy Syst., Vol.1,pp.46–53,1993.[9]Nakamura E.,and N.Kehtarnavaz,Optimization offuzzy membership function parameter,Proc.IEEE Int.Conf.Syst.,Man and Cyber.,Vol.1,pp.1–6, 1995.[10]Harmaifar A.,and E.McCormick,SimultaneousDesign of Membership Function and Rule Sets for Fuzzy Controllers Using Genetic Algorithms,IEEE Trans.Fuzzy Syst.,Vol.3,pp.129–139,1995. [11]O’Dwyer A.,PI and PID controllers for time de-lay processes:performance and robustness issues, Proceedings of the Wismarer Automatisierungssym-posium,pp.227–234,September1999.。