欧拉图的判定

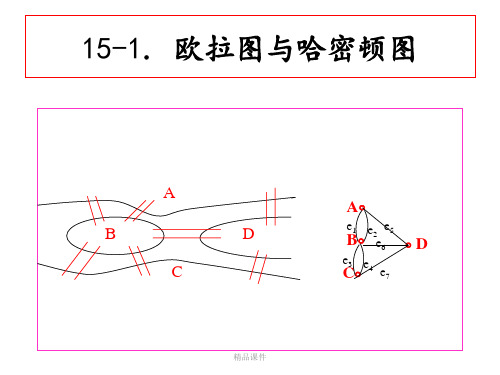
第十三章欧拉图与哈密顿图欧拉图产生的背景就是前面介绍的七桥问题。

1736年，瑞士数学家欧拉发表了图论的第一篇著名论文“哥尼斯堡七桥问题”。

欧拉在这篇论文中提出了一条简单准则，确定七桥问题是不能解的。

下面给出有关定义及定理。

定义2－1.1 设是无向连通图或有向弱连通图。

通过G的每条边一次且仅一次的路径(循环)称为G的欧拉路径(循环)。

具有欧拉循环的图称为欧拉图(规定平凡图是欧拉图)。

例2－1.1图2－1.1，有欧拉路径，，无欧拉路径和欧拉循环，，是欧拉图。

如何判断一个无向连通图或有向弱连通图是否为欧拉图？是否有欧拉路径？定理2－1.1 设是无向连通图，则1）当且仅当G的每个顶点都是偶顶点时，G才是欧拉图。

2）当且仅当G除两个顶点是奇顶点外，其他顶点都是偶顶点时，G才有欧拉路径。

证明 1)设是欧拉图：当时，G只含一个顶点，这个顶点显然是偶顶点。

当时，由所给条件知有G的欧拉循环，因为G的每条边在中出现且仅出现一次，故必通过G的每个顶点，且通过顶点时，此顶点的度就增加2，从而G的每个顶点都是偶顶点。

设G的每个顶点都是偶顶点：当时，G显然是欧拉图。

当时，由所给条件，G中必有循环，故也必有基本循环，从G中去掉各边后得生成子图，中每个顶点仍为偶顶点。

若是零图，则就是G的欧拉循环。

即G是欧拉图；若不是零图，即还有边，则必有与有一公共顶点的基本循环。

由于两条有一公共顶点的简单循环通过这个公共顶点可合并成一条简单循环，故和可合并成一条简单循环。

再从中去掉各边后得；最后得出一条通过G每条边的简单循环，这就是G的欧拉循环，故G是欧拉图。

2)设和是G有欧拉路径当且仅当有欧拉循环(即是欧拉图)，故由1)即得结论。

★用上面定理就能判断一个无向连通图是否为欧拉图，是否有欧拉路径。

例2－1.2 对于图2－1.2图2－1.2根据定理2－1.1中1)的结论知是欧拉图。

还可由其证明方法具体找出一条欧拉循环。

先将和合并成简单循环，再将和合并成简单循环，这就是G的一条欧拉循环。

一、实验目的：判定一个图是否是欧拉图二、实验内容：1)题目：.（1）（2）（3）各图的邻接矩阵：V1 V2 V3 V4 V5 V6 V1 0 1 1 0 0 0V2 1 0 1 1 0 0V3 1 1 0 1 1 0V4 0 1 1 0 1 1V5 0 0 1 1 0 1V6 0 0 0 1 1 0V1 V2 V3 V4 V5 V6 V1 0 1 1 0 0 0V2 1 0 1 2 0 0V3 1 1 0 1 1 0V4 0 2 1 0 1 2V5 0 0 1 1 0 2V6 0 0 0 2 2 0V1 V2 V3 V4 V5 V6 V7 V1 0 1 1 0 0 0 0V2 1 0 1 1 0 0 0V3 1 1 0 1 1 0 0V4 0 1 1 0 1 1 0V5 0 0 1 1 0 1 0 V6 0 0 0 1 1 0 0 V7 0 0 0 0 0 0 0 2)代码：#include "stdio.h"#include "math.h"#define m 6 /*定义结点个数*/float M=1000000.0; /*用于比较权重选择最优路径*/float B[m][m]={0},D[m][m]={0},C[m]={0}; /*记录权重*/int E[m][m]={0}; /*记录两点间的路径是否被选择*/int X[m]={0},Y[m]={0}; /*记录已选择的点*/int s=0;int judge() /*判断是否所有点都已连接*/{int k,s=0,t=0,flag1=0;for(k=0;k<m;k++){if(X[k]==0) {flag1=0;t=k+1;break;}else flag1=1;}if(flag1==0) s=t;return s;}void search() /*选择从所有已连点到未连点中权重最小但大于0的路径*/ {float M1=0.0;int i,j,k1=0,k2=0;M1=M;for(i=0;i<m;i++){if(X[i]==1){for(j=0;j<m;j++){if(Y[j]==0){if(B[i][j]<M1&&B[i][j]>0){M1=B[i][j];k1=i;k2=j;}}}}}if(M1==M) s=1;else{E[k1][k2]=1; B[k1][k2]=B[k2][k1]=M; X[k2]=1; Y[k2]=1;}}void main(){int r=0,flag=0,flag1=0;int i,j;printf("输入图的邻接矩阵：\n");for(i=0;i<m;i++)for(j=0;j<m;j++){scanf("%f",&B[i][j]);D[i][j]=B[i][j];}X[0]=1;Y[0]=1;while(1){s=0; flag=0;search();if(s==1){r=judge();if(r==0){flag=1;break;}else{flag=2;break;}}}if(flag==1){ printf("该图有最小支撑树，是连通图！");for(i=0;i<m;i++){for(j=0;j<m;j++)C[i]=C[i]+D[i][j];if(fmod(C[i],2)==1) {flag1=1;break;}}if(flag1==1) printf("\n该图不是欧拉图!\n");else printf("\n该图是欧拉图!\n");}else printf("\n该图是不连通的，不是欧拉图!\n"); }3）运行结果：三、使用环境适用于解决各种欧拉图的判定问题，在使用时需根据实际情况来更改预定义的m的值。

离散数学欧拉图第7讲基本概念定义7.1◆通过无向图中所有边一次且仅一次行遍所有顶点的迹称为欧拉迹。

◆通过无向图中所有边一次且仅一次行遍所有顶点的闭迹称为欧拉环游。

◆具有欧拉环游的图称为欧拉图。

回忆思考哥尼斯堡七桥问题即下图是否是欧拉图的问题。

CA BD定理7.1设G是非平凡无向图，则G是欧拉图 G是连通图且G中没有奇点。

证明“”连通，显然。

因为所有的边都在欧拉环游上出现一次且仅一次，所以每个顶点的度=该顶点在欧拉环游上出现的次数的2倍。

故每个点都是偶点。

证：证明“”任一个无奇点的无向图，从任一条边开始都能长出一条闭迹。

设P 是G 中最长的闭迹，则P 是G 的欧拉环游。

（想想为什么？）故G 是欧拉图。

证：定理7.1（其中的必要性就足够了）回答了（实际上是否定）哥尼斯堡七桥问题。

CA BD推论设G 是非平凡无向图，则G有欧拉迹 G是连通图且G中至多有2个奇点。

一个图有欧拉迹，在中国古代被称为是“一笔画”的。

比如“日”可一笔画，而“田”不可一笔画。

思考上述定理给出了欧拉图的判定条件,那么如何找出欧拉环游呢?Fleury算法——一种求欧拉环游的方法(1) 任取v0∈V(G)，令P0= v0。

(2) 设P i= v0e1v1e2… e i v i已经选取，按下面方法来从E(G)-{e1,e2… e i}中选取e i+1：(a) e i+1与v i相关联；(b) 除非无别的边可供选择，否则e i+1不为G i=G-{e1,e2… e i}中的桥。

(3) 当(2)不能再进行时，算法停止。

123 456 789谢谢观看。

欧拉图简述---（⼀笔画问题）欧拉图欧拉图是在⼤家⼩学时学奥数都学习过的⼀个类型的题，⽆论你学得好不好，你都听过它的另外⼀个名字：⼀笔画问题；⼀，⾸先来定义⼀下：1.欧拉回路：图G的⼀个回路，如果恰通过图G的每⼀条边，则该回路称为欧拉回路，具有欧拉回路的图称为欧拉图。

欧拉图就是从图上的⼀点出发，经过所有边且只能经过⼀次，最终回到起点的路径。

2.欧拉通路：即可以不回到起点，但是必须经过每⼀条边，且只能⼀次。

也叫"⼀笔画"问题。

3.基图：基图是针对有向图的说法，是忽略有向图的⽅向得到的⽆向图。

4.欧拉图:存在欧拉回路的图。

欧拉回路⼀定要⾸尾相连，，通路不⼀定。

⼆.性质与定理先说说有向图和⽆向图，显⽽易见，有向图就是有向的图，⽽⽆向图反之亦然。

性质与定理定理1⽆向图G为欧拉图，当且仅当G为连通图且所有顶点的度为偶数。

证明：必要性设图G的⼀条欧拉回路为C。

由于C经过图G的每⼀条边，⽽图G没有孤⽴点，所以C也经过图G的每⼀个顶点，G为连通图成⽴。

⽽对于图G 的任意⼀个顶点 v，经过C时都是从⼀条边进⼊，从另⼀条边离开，因此v经过C的关联边的次数为偶数。

⼜由于C不重复地经过了图G的每⼀条边，因此的度为偶数。

充分性假设图G中不存在回路，⽽G是连通图，故⼀定是G树，那么有|E|=|V|−1 |E|=|V|−1|E|=|V|-1由于图G所有顶点的度为偶数⽽且不含孤⽴点，那么图G的每⼀个顶点的度⾄少为2。

推论1⽆向图G为半欧拉图，当且仅当G为连通图且除了两个顶点的度为奇数之外，其它所有顶点的度为偶数。

证明：将两个度为奇数的顶点连接，由定理⼀得该图为欧拉图，故去掉环上⼀边为半欧拉图。

定理2有向图G为欧拉图，当且仅当G的基图连通，且所有顶点的⼊度等于出度。

推论2有向图G为半欧拉图，当且仅当G的基图连通，且存在顶点u的⼊度⽐出度⼤1 、v的⼊度⽐出度⼩ 1，其它所有顶点的⼊度等于出度。

证明同定理1相似。