受弯构件
- 格式:ppt
- 大小:1.71 MB
- 文档页数:83



受弯构件受弯构件是工程结构中常见的一种结构元素,主要用于承受弯曲荷载。
它是由一根或多根材料组成的构件,常见的形状有梁、柱和弯曲杆。
受弯构件的设计和分析是工程领域中的重要课题,因为它的性能直接影响到结构的稳定性和安全性。
在设计受弯构件时,需要考虑多种因素,包括材料的强度、几何形状、加载方式以及构件的支撑情况等。
首先,材料的强度对受弯构件的设计至关重要。
常用的材料有钢、混凝土和木材等。
钢材具有高强度和良好的延展性,适用于承受大荷载的情况。
混凝土材料具有良好的抗压性能,适用于承受压力的构件。
木材则具有较好的抗拉性能,适用于某些特殊构件的设计。
在设计受弯构件时,需要根据材料的特性选择合适的截面形状和尺寸。
其次,几何形状对受弯构件的性能有直接影响。
常见的受弯构件包括矩形梁、I型梁和圆形柱等。
矩形梁是一种简单的几何形状,容易计算和分析,适用于小跨度和中等荷载的情况。
I型梁由上下两个平行的平板和一个连接两个平板的腹板组成,它的截面形状使得承载能力更大,适用于大跨度和大荷载的情况。
圆形柱具有良好的稳定性,适用于承受压力的情况。
受弯构件在实际使用中通常会承受不同的加载方式,包括集中力、均布力和扭矩等。
集中力是指作用在受弯构件上的单个力,常见的例子有梁的支座反力和集中载荷等。
均布力是指作用在一段长度上的力,常见的例子有均布载荷和自重等。
扭矩是指作用在受弯构件上的旋转力,常见的例子有在梁两端施加的扭矩等。
在设计受弯构件时,需要根据加载方式确定合适的设计参数,以确保结构的稳定性和安全性。
最后,支撑情况对受弯构件的性能也有重要影响。
支撑是指构件的两端或多个点的固定或支持。
常见的支撑方式有固定支持、铰支持和滑动支持等。
固定支持是指构件两端受到约束,不允许产生位移和转动。
铰支持是指构件的某一端可以自由转动,但不允许产生位移。
滑动支持是指构件的某一端可以发生位移,但不允许产生转动。
根据支撑方式的不同,受弯构件的受力特点也会有所差异,因此在设计中需要合理选择支撑方式。


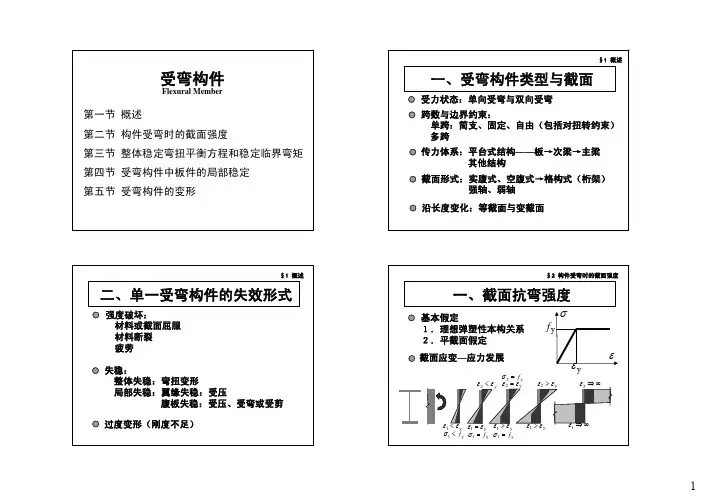



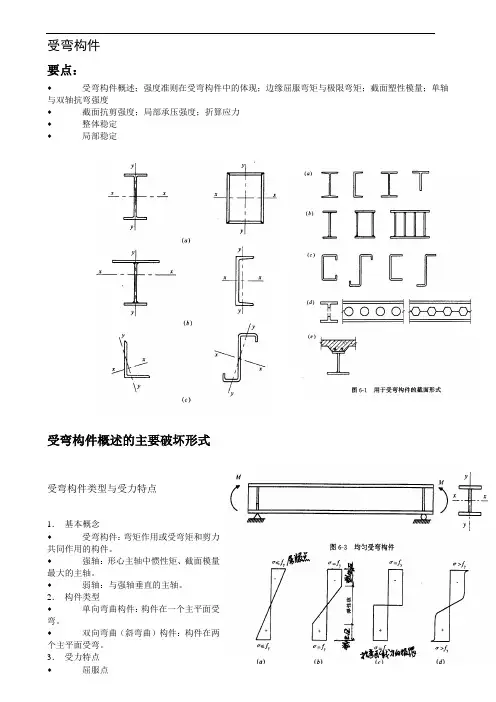
受弯构件要点:♦受弯构件概述;强度准则在受弯构件中的体现;边缘屈服弯矩与极限弯矩;截面塑性模量;单轴与双轴抗弯强度♦截面抗剪强度;局部承压强度;折算应力♦整体稳定♦局部稳定受弯构件概述的主要破坏形式受弯构件类型与受力特点1.基本概念♦受弯构件:弯矩作用或受弯矩和剪力共同作用的构件。
♦强轴:形心主轴中惯性矩、截面模量最大的主轴。
♦弱轴:与强轴垂直的主轴。
2.构件类型♦单向弯曲构件:构件在一个主平面受弯。
♦双向弯曲(斜弯曲)构件:构件在两个主平面受弯。
3.受力特点♦屈服点♦ 弹性核 ♦ 塑性区♦ 极限抗弯承载力主要破坏形式1. 截面强度破坏截面的平均应力达到屈服点f y ,截面应变迅速增加最后导致结构破坏。
通常以截面的平均应力达到屈服点f y 为轴心受压构件强度破坏准则。
2. 整体失稳破坏由于侧向干扰力或构件初始偏心等原因,受弯构件离开原来的平面,发生侧向挠曲和扭转称为受弯构件的整体失稳。
当轴力达到某一值时结构不能保持稳定的平衡状态,结构变形迅速增大开始丧失稳定性,最后导致结构破坏。
这时的轴心压力称为临界压力。
3. 局部失稳破坏构成受弯构件的板件在压应力和剪应力作用下局部出现波浪状的鼓曲变形,但轴线变形仍在弯曲平面内的的现象。
一般不一定作为构件整体破坏的判别准则。
受弯构件的截面强度强度准则1. 边缘纤维屈服准则截面上边缘处的最大应力达到屈服时即认为受弯构件的截面达到了强度极限,截面上的弯矩称为屈服弯矩。
此时构件在弹性阶段工作。
2. 全截面屈服准则一整个截面的应力达到截面承载极限强度的状态作为强度破坏的界限,此时截面上的弯矩称为塑性弯矩或极限弯矩。
3. 部分发展塑性准则将截面塑性区限制在某一范围,一旦塑性区达到规定的范围即视为强度破坏。
抗弯强度1. 缘纤维屈服准则 单向弯曲构件 双向弯曲构件 截面应力:d xn x f W M ≤=σ;d yny xn x f W M W M≤+=σ(或()()d xyn yn xn xyn x xn y xyn y yn x f I I I y I M I M x I M I M ≤--+-=2σ) 相关准则:1≤exdxM M ; 1≤+eydy exd xM M M M屈服弯矩:d xn exd f W M =;d yn eyd f W M =2. 全截面屈服准则 中性轴:⎰=dA f N y;⎰=ydA f My x;⎰=xdA f M y y相关准则:1≤pxdxM M ; 1≤+pydy pxd xM M M M极限弯矩:d pxn pxd f W M =;d pyn pyd f W M =3. 部分发展塑性准则截面应力:d exn x x f W M ≤γ; d eyny y exn x xf W M W M ≤+γγ截面塑性发展系数:ep x M M =γ相关准则:直线关系式:1≤exdx xM M γ; 1≤+eydy y exd x xM M M M γγ屈服弯矩:d xn exd f W M =;d yn eyd f W M =抗剪强度1. 单方向横向力作用 截面应力:vyd x x y f tI S V ≤=τ(vyd wy f A V ≤=τ)2. 双方向横向力作用vyd y y x x x y f tI S V tI S V ≤+=τ(或()()()vyd xyyx xxy x x y y xy y yx f tI II V I S I S V I S IS ≤--+-=2τ)局部承压强度y zw c f l t F≤=σ; 其中,分布长度y z h a l 2+= 否则,需要设置支承加劲肋。

一、受弯构件(一)在主平面内受弯的实腹式构件抗弯强度应符合下列规定1、翼缘板弯曲正应力满足下列要求:双向受弯的实腹式构件:f d ≥γ0(M y W y,eff +M z W z,eff )式中:γ0——结构重要性系数;M y 、M z ——计算截面的弯矩设计值;W y,eff 、W z,eff ——有效截面相对于y 轴和z 轴的截面模量,其中受拉翼缘应考虑剪力滞影响,受压翼缘应同时考虑剪力滞和局部稳定影响。
2、腹板剪应力应满足下列要求。
闭口截面腹板剪应力应按剪力流理论计算。
γ0τ≤f vd式中:γ0——结构重要性系数;τ——剪应力;f vd ——钢材的抗剪强度设计值。
3、平面内受弯实腹式构件腹板在正应力 σx 和剪应力 τ 共同作用时,应满足下列要求。
γ0√(σx f d )2+(τf vd)2≤1 式中:σx ——x 方向正应力;f d ——钢材的抗拉、抗压和抗弯强度设计值。
(二)受弯构件的整体稳定性应符合下列规定1、等截面实腹式受弯构件,应按下列规定验算整体稳定。
γ0(βm,yM y χLT,y M Rd,y +M z M Rd,z )≤1 γ0(M y M Rd,y +βm,z M z χLT,z M Rd,z)≤1 M Rd,y =W y,eff f dM Rd,z =W z,eff f dλLT,y =√W y,eff f y M cr,y ,λLT,z =√W z,eff f y M cr,z式中: M y 、M z ——构件最大弯矩;βm,y、βm,z——等效弯矩系数;χLT,y、χLT,z——M y和M z作用平面内的弯矩单独作用下,构件弯扭失稳模态的整体稳定折减系数;λ̅̅̅LT,y、λLT,z——弯扭相对长细比;W y,eff、W z,eff——有效截面相对于y轴和z轴的截面模量,其中受拉翼缘应考虑剪力滞影响,受压翼缘应同时考虑剪力滞和局部稳定影响。
M cr,y、M cr,z——M y和M z作用平面内的弯矩单独作用下,考虑约束影响的构件弯扭失稳模态的整体弯扭弹性屈曲弯矩,可采用有限元方法计算。