曲线积分和路径的无关性

微积分中的曲线积分与路径无关性研究曲线积分是微积分中的重要概念，用于计算曲线上的积分值。

在微积分的学习中，我们经常遇到这样一个问题：曲线积分的结果是否与路径的选择相关？这个问题引发了很多讨论和研究，最终得出了路径无关性的结论。

本文将深入探讨微积分中的曲线积分与路径无关性的研究结果。

1. 曲线积分的定义曲线积分是微积分中用来计算曲线上的函数值的方法。

它是将函数沿着指定路径的弧长进行积分的过程，通常表示为∮f(x,y)ds。

其中，f(x,y)是曲线上的函数，ds表示路径的弧长元素。

曲线积分可以用来求解曲线上的质量、质心、流量等物理问题，是应用广泛的工具。

2. 路径无关性的概念路径无关性是指，如果两条曲线的起点和终点相同，且曲线上的函数在这两条曲线上有相同的连续导数，则曲线积分的结果是相同的。

也就是说，曲线积分的结果只与积分函数f(x,y)在曲线上的取值有关，而与具体的路径选择无关。

3. 曲线积分与路径无关性的证明要证明曲线积分的路径无关性，可以通过参数化曲线、做路径分割、使用定理等方法进行推导。

其中最重要的是格林公式和斯托克斯公式。

格林公式是指二维空间中的曲线积分与曲线所围成的区域的面积之间的关系。

它通过对曲线进行参数化，将曲线积分转化为两个变量的重积分。

格林公式的证明过程中，不涉及路径的选择，因此曲线积分的结果与路径无关。

斯托克斯公式是指三维空间中的曲线积分与曲线所围成的曲面的积分之间的关系。

它通过将曲线所围成的曲面分成小面元，然后对每个小面元应用格林公式得到结果。

由于小面元的选择不影响最后的结果，所以曲线积分的路径无关性得到了证明。

4. 曲线积分的应用曲线积分在物理学、工程学、计算机图形学等领域有广泛的应用。

例如，它可以用来计算电场沿着闭合路径的环路积分，从而得到电势差；在流体力学中，曲线积分可以用来计算液体沿着曲线的流量；在计算机图形学中，曲线积分可以用来计算光线在曲线路径上的衰减。

总结：微积分中的曲线积分与路径无关性是一个重要的研究课题。

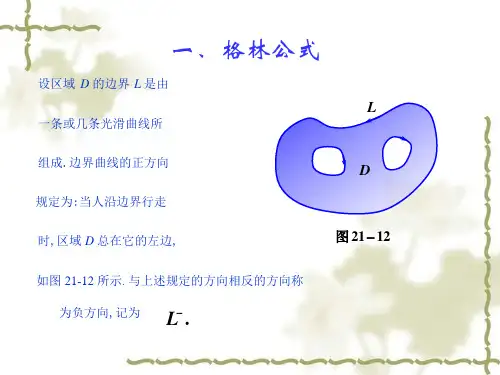
第二十一章 重积分3格林公式、曲线积分与路线的无关性一、格林公式概念：当区域D 的边界L 由一条或几条光滑曲线所组成时，规定边界曲线的正方向为：当人沿边界行走时，区域D 总在他的左边. 与正方向相反的方向称为负方向，记为-L.定理21.11：若函数P(x,y), Q(x,y)在闭区域D 上连续，且有连续的一阶偏导数，则有格林公式：⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . L 为区域D 的边界曲线，并取正方向.证：根据区域D 的不同形状，可分三种情形来证明： (1)若区域D 既是x 型区域，又是y 型区域(如图1)，即 平行于坐标轴的直线和L 至多交于两点，该区域D 可表示为： φ1(x)≤y ≤φ2(x), a ≤x ≤b 或ψ1(x)≤x ≤ψ2(x), c ≤y ≤d.这里y=φ1(x)和y=φ2(x)分别为曲线⌒ACB 和⌒AEB 的方程, x=ψ1(x)和x=ψ2(x) 分别为曲线⌒CAE 和⌒CBE的方程, ∴⎰⎰∂∂Dd x Qσ=⎰⎰∂∂)()(21y y d c dx x Q dy ψψ=⎰d c dy y y Q )),((2ψ-⎰d c dyy y Q )),((1ψ=⎰⋂CBE dy y x Q ),(-⎰⋂CAE dy y x Q ),(=⎰⋂CBE dy y x Q ),(+⎰⋂EAC dy y x Q ),(=⎰L dy y x Q ),(.同理可证：-⎰⎰∂∂Dd y Pσ=⎰L dx y x P ),(. 即有⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . (2)若区域D 是一条按段光滑的闭曲线围成(如图2)，则先用几段光滑曲线将D 分成有限个既是x 型又是y 型的子区域，然后逐块按(1)得到它们的格林公式，相加即可.图2中区域D 可分成三个既是x 型又是y 型的区域D 1,D 2,D 3，则有⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D d y P x Q σ=⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂1D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂2D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂3D d y P x Q σ =⎰+1L Qdy Pdx +⎰+2L Qdy Pdx +⎰+3L Qdy Pdx =⎰+L Qdy Pdx.(3)若区域D 由几条闭曲线所围成(如图3)， 可适当添加直线AB, CE,把区域转化为(2)的情况处理.图D 的边界线由AB,L 2,BA,⌒AFC ,CE,L 3,EC 及⌒CGA构成. 由(2)知 ⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎪⎭⎫ ⎝⎛+++++++⎰⎰⎰⎰⎰⎰⎰⎰⋂⋂CGA EC l CE AFCBA l AB32(Pdx+Qdy)=()⎰⎰⎰++132L L L (Pdx+Qdy)=⎰+L Qdy Pdx .注：格林公式可写为：⎰⎰∂∂∂∂Dd QP y x σ=⎰+L Qdy Pdx .例1：计算⎰AB xdy ，其中曲线AB 为半径为r 的圆在第一象限部分. 解：如图，对半径为r 的四分之一圆域D 应用格林公式有⎰⎰-D d σ=⎰-L xdy =⎰OA xdy +⎰AB xdy +⎰BO xdy =⎰AB xdy . ∴⎰AB xdy =⎰⎰-Dd σ=-41πr 2.例2：计算I=⎰+-Ly x ydxxdy 22, 其中L 为任一不包含原点的闭区域的边界线.解：⎪⎪⎭⎫ ⎝⎛+∂∂22y x x x =22222)(y x x y +-, ⎪⎪⎭⎫ ⎝⎛+-∂∂22y x y y =22222)(y x x y +- 在上述区域D 上连续且有界，∴⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-∂∂-⎪⎪⎭⎫ ⎝⎛+∂∂Dd yx yx y x x x σ2222=0. 由格林公式可得I=0.注：在格林公式中，令P=-y, Q=x ，则得到一个计算平面区域D 的面积S D 的公式：S D =⎰⎰Dd σ=⎰-L ydx xdy 21.例3：如图，计算抛物线(x+y)2=ax (a>0)与x 轴所围的面积.解：曲线⌒AMO由函数y=x ax -, x ∈[0,a]， 直线OA 为直线y=0， ∴S D =⎰-ydx xdy 21=⎰-OA ydx xdy 21+⎰⋂-AMO ydx xdy 21=⎰⋂-AMO ydx xdy 21=dx x ax ax ax a ⎰⎥⎦⎤⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-0)(1221=dx ax a ⎰-02121=dx x a a⎰4=62a .二、曲线积分与路线的无关性概念：若对于平面区域D 上任一封闭曲线，皆可不经过D 以外的点而连续收缩于属于D 的某一点，则称此平面区域为单连通区域，否则称为复连通区域。

曲线积分与路径无关性的应用摘要：本文介绍了第二型曲线积分与路径无关的四个等价条件，并结合实例说明了此定理的应用：计算曲线积分、求原函数、求微分方程的解、求微分方程中的未知函数，特别是在求未知函数的例子中，解决了与之相关的一系列利用曲线积分与路径无关性求微分方程中的未知函数的问题。

关键词：曲线积分全微分全微分方程路径对于第二型曲线积分，一般来说其积分值不仅与积分曲线的起点和终点位置有关，而且即便是同样的起点和终点，若沿的路线不同，其积分值也可能不同。

但是在一定的条件下，第二型曲线积分完全可以做到与积分曲线的路线无关，只与曲线的起点和终点位置有关，这就是下面介绍的定理：定理设是单连通闭区域，函数在区域内连续，且有一阶连续偏导数，则以下四个条件等价：(1) 沿内任一按段光滑的闭曲线，有；(2)对内任一按段光滑的曲线，曲线积分与路线无关，只与的起点和终点有关；(3)是内某一函数的全微分；(4)在内每一点处有。

此定理的主要应用是在求第二型曲线积分中，若在单连通闭区域内可以做到，则沿内任一按段光滑的曲线，曲线积分只与的起点和终点有关，从而可以选择合适的路线（一般是折线）。

但是由于在定理的条件下，还等价于是内某一函数的全微分，故此定理还可以运用于与全微分方程相关的一些微分方程的求解。

现将此定理的应用总结如下：1 此定理可用来求曲线积分例1 设为圆周的上半圆，顺时针方向。

求曲线积分。

解：令，，则在不包含曲线的任何区域都有由定理知，在曲线的上方或下方区域内沿任何按段光滑曲线的曲线积分与路径无关，而在曲线的上方，故只要起点和终点与相同，则沿曲线的上方任一按段光滑曲线的曲线积分都与所求积分相同。

设的起点为，终点，，，由上面的讨论可知，原曲线积分与沿折线上的曲线积分相同。

故因在区间上是奇函数，故，从而。

注意：虽然沿直线上的曲线积分计算量要少，但是与所求曲线积分值却不同，这是因为直线含曲线上的点。

因此运用此定理时要特别注意定理的条件：是单连通闭区域，在内且有一阶连续偏导数。