-x2+(2+
10)x+3-
10=-
x- 2+ 10
2
+ 13,
2
2
∵-1<0,∴当 x=2+ 10 时,DE+DF 有最大值,最大值为 13.
2
2
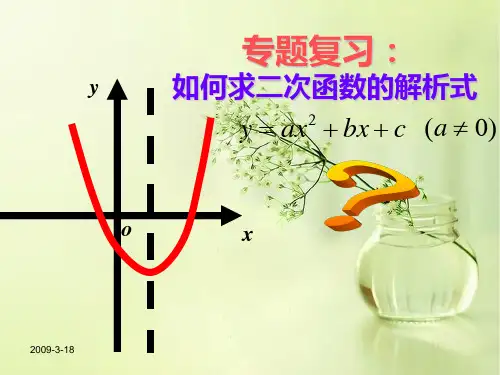
11.(几何直观、推理能力、应用意识、创新意识)已知二次函 数y=2x2+m. (1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1 < y2(填 “>”“=”或“<”); (2)如图,此二次函数的图象经过点(0,-4),正方形ABCD的顶 点C,D在x轴上,A,B恰好在二次函数的图象上,求图中阴影部 分的面积之和.
c=0.
∴此二次函数的解析式为 y=-x2-4x.
(2)∵S△AOP=8,即12 ·4·yp =8,∴yp=±4.
当 y=4 时,4=-x2-4x,解得 x1=x2=-2, ∴P1(-2,4); 当 y=-4 时,-4=-x2-4x,解得 x=-2±2 2, ∴P2(-2-2 2,-4),P3(-2+2 2,-4). 综上所述,点 P 的坐标为 P1(-2,4), P2(-2-2 2,-4),P3(-2+2 2,-4).
∴B(2,4).∴S阴影=S矩形BCOE=2×4=8.
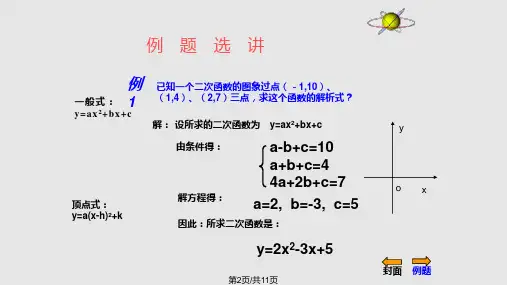
8.如图,二次函数y=ax2-4x+c的图象经过坐标原点,与x轴交 于点A(-4,0). (1)求此二次函数的解析式; (2)在抛物线上存在点P,满足S△AOP=8,请求出点P的坐标.
解:(1)把(0,0),(-4,0)分别代入 y=ax2-4x+c,得
c=0,
解得 a=-1,
16a+16+c=0,
解:(1)A(2,-4),B(0,4). (2)设抛物线的解析式为y=a(x-2)2-4, 将B(0,4)代入,得4a-4=4,解得a=2. ∴抛物线的解析式为y=2(x-2)2-4.