江苏省徐州市丰县修远双语学校八年级数学《12 轴对称的性质》同步练习 (无答案)

苏科版数学八年级上2.2轴对称的性质同步练习含答案初二数学试题精品§2.2 轴对称的性质 (2)一、选择1．下列图形中，不是轴对称图形的是 ( )2．下列图形中，不一定是轴对称图形的是 ( )A．线段 B．等腰三角形 C．等腰梯形 D．平行四边形3．如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P 关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=2．5 cm，PN=3 cm，MN=4 cm，则线段QR的长为 ( )A．4．5 cm B．5．5 cm C．6．5 cm D．7 cm4．如图，在Rt △ABC中，∠ACB=90°，∠ACM折叠，点A落在点D处，如果CD恰好与AB垂直，那么∠A的度数是 ( )A．30° B．40° C．50° D．60°5．如图，△ABC的周长为30 cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边与点E，连接AD，若AE=4 cm，则△ABD的周长是 ( ) A．22 cm B．20 cm C．18 cm D．15 cm6．如图，在四边形ABCD中，△ABC与△ADC关于对角线AC对称，则以下结论正确的是 ( )①AC平分∠BAD ②CA平分∠BCD ③BD⊥AC ④BE=DE A．①②③④ B．①②③ C．①② D．④二、填空7．请在下面的这一组图形符号中找出它们所蕴含的内在规律，然后在横线上的空白处，填上适当的图形．8．如图，把图形沿BC对折，点A和点D重合，那么图中共有全等三角形对．9．如图，直线l是四边形ABCD的对称轴，若AB=CD，有下面的结论：①AB∥CD；②AC ⊥BD；③AO= OC；④AB⊥BC．其中正确的结论有．10．如图，分别作出点P关于OA，OB的对称点P1，P2，连接P1，P2，分别交OA，OB 于点M，N，若P1，P2=5 cm，则△PMN的周长为 .精品11．如图，在2×2的正方形格纸中，有一个以格点为顶点的△ABC，请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形，这样的三角形共有个．12．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q 分别是AD，AC上的动点，则PC+PQ的最小值是．三、解答13．如图，已知△ABC和直线MN．求作：△A'B'C'，使△A'B'C'和△ABC关于直线MN对称．(不要求写作法，只保留作图痕迹)14．如图，在边长为1的小正方形组成的10×10网格中 (我们把组成网络的小正方形的顶点称为格点)，四边形ABCD在直线l的左侧，其四个顶点A，B，C，D分别在网格的格点上．(1) 请你在所给的网格中画出四边形A'B'C'D'，使四边形A'B'C'D'和四边形ABCD关于直线l对称，其中点A'B'C'D'分别是点A，B，C，D的对称点；(2) 在(1)的条件下，结合你所画的图形，求四边形A'B'C'D'的面积；连接AA '，DD '，求四边形ADD'A '的面积．15．如图，在Rt△ABC 中，∠C=90°，沿过点B的一条直线BE折叠Rt△ABC，使点C 恰好落在AB边的中点O处，则∠A等于 ( )A．40° B．35° C．30° D．20°精品16．生活中，有人喜欢把传送的便条折成(阴影部分表示纸条的反面)：形状，折叠过程是这样的如果由信纸折成的长方形纸条 (图①) 长为26 cm，宽为x cm，分别回答下列问题：(1) 为了保证能折成图④的形状 (即纸条两端均超出点P)，试求x的取值范围．(2) 如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点P的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点M与点A的距离(用x表示)．参考答案1．A 2．D 3．A 4．C 5．A 6．A 7．11．5 12．－8． 3 9．①②③ 10．52451 13．略14．(1)略 (2)四边形A'B'C'D'的面积为3×4－×2×2=12×1×3－12×1×212×1×2－感谢您的阅读，祝您生活愉快。

一、填空题1.等腰三角形是轴对称图形，它有___条对称轴，它的对称轴是________________________。

2．点A （－2，1）关于y 轴的对称点的坐标是_____，点A 关于x 轴的对称点的坐标是_____． 3. 在平面直角坐标系中，点P （－2，1）关于 y轴对称的点的坐标为 ，点P （－2，1）关于 x 轴对称的点的坐标为是 ． 4．点A （3，－12），B （3，12）关于_______轴对称，点C （－6，－10），D （6，－10） 关于________轴对称，点（1，2）关于原点的对称点的坐标为 ． 5．已知A （2m +n ，2）、B （1，n －m ），若A 、B 关于x 轴对称；则m ，n 的值分别是_________； 若A 、B 关于y 轴对称．则m ，n 的值分别是_________。

6.若点A （2，a ）关于x 轴的对称点是B （b ，﹣3），则ab 的值是 ． 7．小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表， 其读数如图所示，则电子表的实际时刻是 ．8．从镜子中看到电子表的时刻为10点51分，则实际时间是______ 9.如图，镜子中号码的实际号码是___________．10．若等腰三角形的一个角是110°，则它的底角为_______°．11．若等腰三角形的一个外角为40 0，则它的底角度数是___________．若等腰三角形一个底角为50°，则此等腰三角形顶角为_________________． 12．等腰三角形的腰长是6，则底边长3，周长为______________________．13．已知等腰ABC △的周长为10，若设腰长为x ，则x 的取值范围是 ； 已知：△ABC 中，AB=AC=x ，BC=6，则腰长x 的取值范围是 ,14．等腰三角形的两边的边长分别为20cm 和9cm ，则第三边的长是__________．15．等腰三角形的周长为13cm,其中一边长为5cm,则该等腰三角形的腰边长为_____cm.． 16.等腰三角形的周长为14，其一边长为4，那么，它的底边为 . 17．等腰三角形的两边长分别是3和7，则其周长为______．18．等腰三角形一腰上的中线把这个三角形的周长分成15㎝和12㎝，则这个三角形的底 边长为 ㎝．19.在等腰三角形ABC 中，AB=AC ，一腰上的中线BD•将这个等腰三角形周长分成15和6两部分，则这个三角形的腰长及底边长为________________________．20．到三角形各顶点距离相等的点是三角形 ______ _____ 的交点，到三角形三边距离相等的点是三角形 _______ ___________ 的交点。

4新人教初二（上）第12章《轴对称》同步学习检测（§12.3）（时间45分钟 满分100分）班级 学号 姓名 得分一、填空题（每题3分，共30分）1．等腰三角形的一个角是110°,则它的底角为_______°．2．等腰三角形的腰长是6，则底边长3，周长为______________________．3．等腰三角形一个底角为50°，则此等腰三角形顶角为________________________． 4．在△ABC 中，AB =AC ，点D 在AC 边上，且BD =BC =AD ，则∠A = °．5．已知直线yy ′⊥xx ′，垂足为O ，则图形①与图形_____成轴对称6．等腰三角形一腰上的中线把这个三角形的周长分成15㎝和12㎝，则这个三角形的底边长为 ㎝．7．腰长为12㎝，底角为15°的等腰三角形的面积为 ． 8．到三角形各顶点距离相等的点是三角形 的交点．9．在直角坐标系内有两点A （-1，1）、B （2，3），若M 为x 轴上一点，且MA +MB 最小，则M 的坐标是________，MA +MB =________．10．等腰三角形的周长为13cm,其中一边长为5cm,则该等腰三角形的腰边长为_____cm.． 二、选择题（每题3分，共24分）11．点M （1，2）关于原点对称的点的坐标为 （ ）A ．（—1，2）B ．（－1，－2）C ．（1，－2）D ．（2，－1） 12．下列说法正确的是（ ）A ．等腰三角形的高、中线、角平分线互相重合B ．顶角相等的两个等腰三角形全等C ．等腰三角形一边不可以是另一边的二倍D ．等腰三角形的两个底角相等13．已知∠AOB =30°，点P 在∠AOB 的内部，P 1与P 关于OB 对称，P 2与P 关于OA 对称，则P ，P 1，P 2三点构成的三角形是（ ）① y ′③②x ′Oxy （第5题）（第14题）E DABC4A ．直角三角形B ．钝角三角形C ．等腰三角形D ．等边三角形14．如图，DE 是∆ABC 中AC 边的垂直平分线，若BC =8厘米，AB =10厘米，则∆EBC 的周长为（ ）厘米A ．16B ．28C ．26D ．18 15．等腰三角形的对称轴，最多可以有（ ）A ．1条B ．3条C ．6条D ．无数条 16．下列判断不正确的是（ ）A ．等腰三角形的两底角相等B ．等腰三角形的两腰相等C ．等边三角形的三个内角都是60°D ．两个内角分别为120°、40°的三角形是等腰三角形 17．下列轴对称图形中对称轴最多的是（ ）A ．等腰直角三角形；B ．正方形；C ．有一个角为60°的等腰三角形；D ．圆18．如图，∠A =15°，AB =BC =CD =DE =EF ，则∠FEM =（ ）A ．45°B ．60°C ．75°D ．90°三、解答题（共46分） 19．（7分）已知，如图ΔABC 中，AB ＝AC ，D 点在BC 上，且BD ＝AD ，DC ＝AC ．将图中的等腰三角形全都写出来．并求∠B 的度数．20．（7分）如图，在⊿ABC 中，∠ABC 和∠ACB 的平分线交于点O ，过O 点作EF ∥BC ，交AB 于E ，交AC 于F ，BE =5cm ，CF =3cm ，求EF 的长．NMEFC BAD （第18题）BCD。

八年级数学轴对称同步练习题(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学轴对称同步练习题(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学轴对称同步练习题(word版可编辑修改)的全部内容。

人教新课标八年级数学（上）自主学习达标检测（二）（轴对称)（时间90分钟满分100分)班级学号姓名得分一、填空题(每题2分，共32分）1．线段轴是对称图形，它有_______条对称轴，正三角形的对称轴有条．2．下面是我们熟悉的四个交通标志图形，请从几何图形的性质考虑,哪一个．．不．．与其他三个同？请指出这个图形，并说明理由．答：这个图形是: （写出序号即可），理由是．3．等腰△ABC中，若∠A=30°，则∠B=________．4．△ABC中,AD⊥BC于D，且BD=CD，若AB=3,则AC=__ __．5．在 Rt △ABC中，∠C=90°，AD平分∠BAC交BC于D，若CD=4，则点D到AB的距离是__________．6．判断下列图形（如图所示）是不是轴对称图形。

7．等腰△ABC中，AB=AC=10，∠A=30°，则腰AB上的高等于___________．8．如图，△ABC中，AD垂直平分边BC,且△ABC的周长为24,则AB+BD = ；又若∠CAB=60°，则∠CAD = ．9．如图，△ABC中，EF垂直平分AB，GH垂直平分AC，设EF与GH相交于O,则点O与边BC的关系如何？请用一句话表示: ．10．如图:等腰梯形ABCD中，AD∥BC,AB=6，AD=5,BC=8，且AB∥DE，则△DEC的周长是____________．11．请在下面这一组图形符号中找出它们所蕴含的内在规律，然后在横线上的空白处填上恰当的图形。

第12章轴对称练习（二）一、选择题1.下列四个图案中，轴对称图形的个数是（）A．1个B．2个C．3个D．4个2．下列图形是轴对称图形的是（）A． B． C．Ｄ．3．下列图形：①线段；②角；③平行四边形；④三角形；⑤圆，其中一定是轴对称图形的共有（）A．2个B．3个C．4个D．5个4．在下列说法中，正确的是（）A．如果两个三角形全等，则它们必是关于直线成轴对称的图形;B．如果两个三角形关于某直线成轴对称，那么它们是全等三角形;C．等腰三角形是关于底边中线成轴对称的图形;D．一条线段是关于经过该线段中点的直线成轴对称的图形5．直角三角形三边垂直平分线的交点位于（）A.三角形内B.三角形外C.斜边的中点D.不能确实6．到三角形三条边的距离都相等的点是这个三角形的（）A．三条中线的交点 B．三条高的交点C．三条边的垂直平分线的交点 D．三条角平分线的交点7.点P关于x轴对称点为P1（3，4），则点P的坐标为（）A.（3，﹣4）B.（﹣3，﹣4）C.（﹣4，﹣3）D.（﹣3，4）8．在直角坐标系中，点P（2,1）关于x轴对称点的坐标是（）A．（2,1）B．（－2,1）C．（2，－1）D（－2，－1）9．王明是班上公认的“小马虎”在做作业时，将点A的纵横坐标次序颠倒，写成A（a，b）, 小华也不细心，将点B的坐标写成关于y轴的对称点的坐标，写成B（－b，－a），则A、B两点原来的位置关系是（）A．关于y轴对称B．关于x轴对称C．A和B重合D．以上都不对10.在直角坐标系中，已知A（-3，3），在y轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有（）.A．2个 B．3个 C．4个 D．5个11．平面内点A（-1，2）和点B（-1，6）的对称轴是（）A．x轴B．y轴C．直线y=4 D．直线x=-112.如果一个等腰三角形的两边长分别是5cm和6cm，那么此三角形的周长是（）A.15cmB.16cmC.17cmD. 16cm或17cm13.如果等腰三角形两边长是6cm和3cm，那么它的周长是（）A、9cmB、12cmC、15cm或12cmD、15cm14.已知等腰三角形一腰上的高与另一腰的夹角为60°，则这个等腰三角形的顶角是（）A ．30° B．60° C．150° D．30°或150°15．已知：一等腰三角形的两边长x 、y 满足方程组2-3,328,x y x y =⎧⎨+=⎩则此等腰三角形的周长为（ ） A ．5 B ．4 C ．3 D ．5或416．已知等腰三角形的一个内角为70°，则另外两个内角的度数是（ ）A ．55°，55°B ．70°，40°C ．55°，55°或70°，40°D ．以上都不对17．在等腰ABC △中，AB AC =，一边上的中线BD 将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（ ）A ．7B ．11C ．7或11D ．7或1018．已知∠AOB =30°，点P 在∠AOB 的内部，P 1与P 关于OB 对称，P 2与P 关于OA 对称，则P ，P 1，P 2三点构成的三角形是（ ）A ．直角三角形B ．钝角三角形C ．等腰三角形D ．等边三角形19．已知等腰△ABC 的底边BC=8cm ，且｜AC -BC ｜=2cm ，则腰AC 的长为（ ）A ． 10cm 或6cmB ． 10cmC ． 6cmD ． 8cm 或6cm20．将一圆形纸片对折后再对折，得到如图所示的图形，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是（ ）21．如图所示，有A 、B 、C 三个居民小区的位置成三角形，现决定在三个小区之间修建一 个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）A ．在AC 、BC 两边高线的交点处B ．在AC 、BC 两边中线的交点处C ．在AC 、BC 两边垂直平分线的交点处D ．在A 、B 两内角平分线的交点处22．如图，AC ＝AD ，BC ＝BD ，则有（ ）A ．AB 垂直平分CD B ．CD 垂直平分ABC ．AB 与CD 互相垂直平分 D ．CD 平分∠ACB23.如图，已知AB ＝AC ，∠A ＝︒36，AB 的中垂线MD 交AC 于点D 、交AB 于点M 。

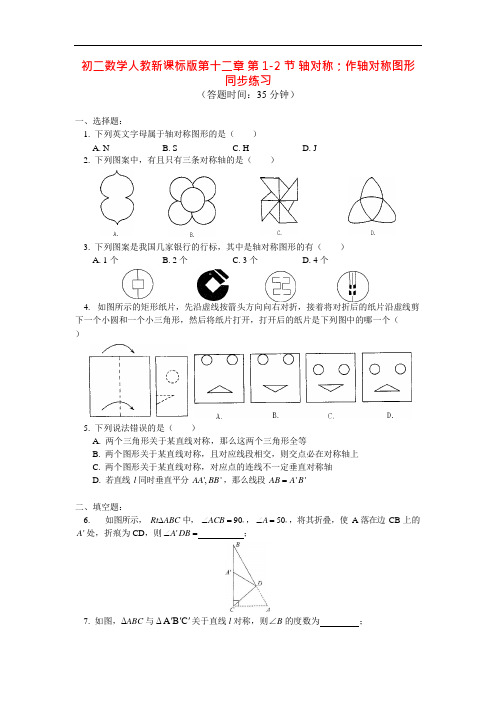
初二数学人教新课标版第十二章 第 1-2 节 轴对称；作轴对称图形同步练习（答题时间：35 分钟）一、选择题：1. 下列英文字母属于轴对称图形的是（）A. NB. SC. HD. J2. 下列图案中，有且只有三条对称轴的是（）3. 下列图案是我国几家银行的行标，其中是轴对称图形的有（ ） A. 1 个 B. 2 个 C. 3 个 D. 4 个4. 如图所示的矩形纸片，先沿虚线按箭头方向向右对折，接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形，然后将纸片打开，打开后的纸片是下列图中的哪一个（ ）5. 下列说法错误的是（ ）A. 两个三角形关于某直线对称，那么这两个三角形全等B. 两个图形关于某直线对称，且对应线段相交，则交点必在对称轴上C. 两个图形关于某直线对称，对应点的连线不一定垂直对称轴D. 若直线 l 同时垂直平分 AA ', BB ' ，那么线段 AB = A ' B '二、填空题：6. 如图所示， Rt ∆ABC 中， ∠ACB = 90 ， ∠A = 50 ，将其折叠，使 A 落在边 CB 上的 A ' 处，折痕为 CD ，则∠A ' DB =；7.如图，ΔABC与Δ A 'B 'C ' 关于直线 l 对称，则∠B 的度数为；lA A'B B'C C'8.点P(3, -5) 关于x 轴对称的点的坐标是；9.如图，正方形的边长为4cm，则图中阴影部分的面积为cm2；10. 已知点A(x + 2, 3) 与点B(-5, y + 7) 关于x 轴对称，则x =，y =；三、解答题：11.如图，将矩形ABCD 沿直线AE 折叠，顶点D 恰好落在BC 边上的F 点处，CE＝3 cm，AB＝8 cm，BC＝10 cm。

求图中阴影部分的面积。

12.如图，l1, l2交于A ，P, Q 的位置如图所示，试确定N 点，使它到l1, l2的距离相等，且到P, Q 两点的距离也相等。

§12.1 轴对称（一）一、引入：我们生活在图形的世界中，许多美丽的事物往往是与图形的对称联系在一起的，无论是随风起舞的风筝，凌空翱翔的飞机，还是中外各式风格的典型建筑；无论是艺术间的创造，还是日常生活中的图案设计，都和对称密不可分。

看了下面的这些图片，你还能从日常生活中找出对称的实例吗？二、新课：1． 将一张纸对折，剪出一个图案，再打开这张纸，观察得到的图形他们与前面的图案有什么共同特点？位于折痕两侧的部分有什么关系？ 2． 轴对称图形的定义：（p29）如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴。

这时，我们说这个图形关于这条直线（成轴）对称。

注：①轴对称图形是一个具有特殊特征的图形——对折后能够完全重合，即对称轴两旁的部分是全 等形；②一个轴对称图形的对称轴可能不止一条。

例题1、观察下列各图，判断他们是否为轴对称图形。

（关键：①能够沿着某条直线对折；②对折后的两部分图形能够完全重合）答案：（1）、（6）例2、下列7个汉字：北、目、田、中、吕、材、上，是轴对称图形的有哪些。

例3、判断下列图形哪些是轴对称图形，如果是说出它的所有对称轴。

①三角形、直角三角形、等腰三角形， ②正方形、长方形、等腰梯形， ③圆形，④五边形，正五边形观察：轴对称的定义：把一个图形沿某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点。

注：①轴对称是指两个图形之间的形状与位置关系，包含两层意思：有两个图形，形状、大小完全 相同（全等形）；重合的方式有限制，即他们的位置必须满足一个条件：把他们沿某一条直线折叠a b c后能够完全重合。

简单说：轴对称必全等，全等不一定轴对称。

轴对称图形与轴对称的区别和联系：区别：轴对称是两个图形的对称关系，轴对称图形是一个图形自身的对称特征；轴对称的对称点分别在两个图形上，轴对称图形的对称点都在一个图形上；两个图形成轴对称，其对称轴可能在两个图形的外部，也可能经过两个图形的内部或他们的公共边（点），而轴对称图形的对称轴一定经过图形的内部。

2.2 轴对称的性质【基础训练】1．成轴对称的两个图形_______．2．如果两个图形关于某直线成轴对称，那么对称轴是对称点_______的垂直平分线．3．设A、B两点关于直线MN成轴对称，则_______垂直平分_______．4．画轴对称图形，首先应确定_______，然后找出_____________．5．如图，如果△ABC沿直线MN折叠后，与△A'B'C完全重合，我们就说△ABC与△A'B'C'关于直线MN_______；直线MN是_______；点A与点A'叫做_______点，图中还有类似的点是_______，图中还有相等的线段和角，分别为_______．6．画出下列轴对称图形的对称轴．7．画出下列图形关于直线l的轴对称图形．8．画出下列图形关于直线l的轴对称图形．9．把下列图形补成以直线l为对称轴的轴对称图形．10．如图，在公路l的同侧，有两个居民小区A、B，现需要在公路边建一个液化气站P，要使液化气站到A、B两小区的距离和最短，这个液化气站应建在哪一处？请在图中作出来．（不写作法）11．画出下列△ABC关于直线l的轴对称图形．【提优拔尖】12．如图，△ABC与△A'B'C'关于直线l对称，且∠A＝78°，∠C＝48°，则∠B的度数为( )．A．48°B．54°C．74°D．78°13．如图，在Rt△ABC中，∠ACB＝90°，∠A＝50°，将其折叠，使点A落在边CB上点A'处，折痕为CD，则∠A'DB等于( )．A．40°B．30°C．20°D．10°14．如图，Rt△AFC和Rt△AEB关于虚线成轴对称，现给出下列结论：①∠1＝∠2；②△ANC≌△AMB；③CD＝DN．其中正确的结论是_______．（填序号）选一个你比较喜欢的结论加以说明．15．如图，作四边形ABCD关于直线l的轴对称四边形，并回答：如果这两个四边形的原图形与其轴对称图形的对应线段或延长线相交，那么交点位置如何？16．如图，在△ABC中，AB＝AC，AB＋BC＝8．将△ABC折叠，使得点A落在点B处，折痕DF分别与AB、AC交于点D、F，连接BF，则△BCF的周长是( )．A．8 B．16 C．4 D．1017．如图，∠A＝30°，∠C'＝60°，△ABC与△A'B'C'关于直线∠对称，则∠B＝_______．18．如图，将一张矩形纸片ABCD沿EF折叠，使顶点C、D分别落在点C'、D'处，C'E 交AF于点G．若∠CEF＝70°，则么GFD'＝_______°．19．Ｐ是∠ＡＯＢ内一点，分别作点Ｐ关于直线ＯＡ、ＯＢ的对称点Ｐ１、Ｐ２连接ＯＰ１、ＯＰ２，则下列结论正确的是( )．Ａ.ＯＰ１⊥ＯＰ２Ｂ.ＯＰ１＝ＯＰ２Ｃ.ＯＰ１⊥ＯＰ２且ＯＰ１＝ＯＰ２Ｄ.ＯＰ１≠ＯＰ２20．如图是经过轴对称变换后所得的图形，与原图形相比（）参考答案1．全等2．连线3．直线MN 线段AB4．对称轴对称点5．对称对称轴对称点B与点B'，点C与点C'AB＝A'B'、AC＝A'C、BC＝B'C；∠A＝∠A'、∠B＝∠B'、∠C＝∠C'6．7．略8．略9．略10．11．略12．B 13．D14．①②15．略16．A17．90°18．4019．B20．A。

12.1 轴对称◇课标点击◇1.什么是轴对称？什么是轴对称图形？它们之间有什么区别？有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．如果一个图形沿某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴．轴对称是两个图形之间的关系，轴对称图形是一个图形具有的特征.2.图形的轴对称有哪些性质？图形的轴对称主要有下列两条性质：⑴如果两个图形成轴对称，那么对称轴是任何一对对应点所连线段的垂直平分线；轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线．⑵轴对称是指两个图形之间的形状与位置关系， 成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．3.线段的垂直平分线有什么性质？线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．◇同步训练1◇【基础达标】1.选择题:⑴下列说法错误．．的是( )A.关于某条直线对称的两个三角形一定全等B.轴对称图形至少有一条对称轴C.全等三角形一定能关于某条直线对称D.角是关于它的平分线对称的图形⑵下列图形中，是．轴对称图形的为( )⑶下图所示的图案中，是轴对称图形且有两条对称轴的是( )E DCA BMNF2.填空题:⑴观察右上图中的两个图案，是轴对称图形的为________，它有_____条对称轴． ⑵如右下图，△ABC 与△AED 关于直线对称，若AB=2cm ，∠C=95°，则AE= ，∠D= 度．⑶坐标平面内，点A 和B 关于x 轴对称，若点A 到x 轴的距离是3cm ，则点B 到x 轴的距离是__________．3.下图中的图形都是轴对称图形，请你试着画出它们的对称轴．4.如图，△ABC 与△ADE 关于直线MN 对称．BC 与DE 的交点F 在直线MN 上.⑴指出两个三角形中的对称点； ⑵指出图中相等的线段和角； ⑶图中还有对称的三角形吗？5.如图，把一张纸片对折后，用笔尖在纸上扎出图⑶所示的图案，将纸打开后铺平，观察你所得的图案.位于折痕两侧的部分有什么关系？与同伴交流你的想法．【能力巩固】lDCABA6.如图是由三个小正方形组成的图形，请你在图中补画一个小正方形，使补画后的图形为轴对称图形。

新人教八年级（上）第12章《轴对称》同步学习检测（§12.1～12.2）（时间45分钟 满分100分）班级 学号 姓名 得分一、填空题（每题3分，共30分）1．如图所示的图形是＿＿＿图形，其对称轴共有＿＿＿条．2．简体汉字中“田、日、中”，都具有对称美的特点，请你再写出具有这们特征的三个汉字为＿＿＿＿＿．3．正方形是轴对称图形，它的对称轴有_______条．4．如果一个图形沿一条直线折叠，直线两旁的部分能够________，这个图形就叫做______________，这条直线就是它的________，这时，我们也说这个图形关于这条直线 对称．5．小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图所示，则电子表的实际时刻是 ．6．点A （－2，1）关于y 轴的对称点的坐标是＿＿＿＿，点x 的对称点的坐标是＿＿＿＿．7．如图，△COB 与△AOB 关于x 轴对称，点A 的坐标为（则点C 的坐标为＿＿＿＿．8．如图所示，写出长方形ABCD 三个顶点的坐标：A B ：＿＿＿，C：＿＿＿＿．9．如图，P 是正△ABC 内的一点，若将△P AB 绕点A 到△P ′AC ，则∠P AP ′的度数为________．10．如图，阴影部分组成的图案既是关于x 轴成轴对称的图形又是关于坐标原点O 成中心对称的图形．若点A 的坐标是（1，3），则点M 和点N 的坐标分别是________．二、选择题（每题3分，共24分）11．下列图形：①线段；②角；③平行四边形；④三角形；⑤圆，其中一定是轴对称图形的共有（ ）A ．2个B ．3个C ．4个D ．5个（第5题）（第1题）12．下列图形中轴对称图形有（）A．4个B．3个C．2个D．1个13．如图所示，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超，使超市到三个小区的距离相等，则超市应建在（）A．在AC、BC两边高线的交点处B．在AC、BC两边中线的交点处C．在AC、BC两边垂直平分线的交点处D．在A、B两内角平分线的交点处14．在刚刚买来的一件衣服上，有一个标签，上面有如下几个图形，如图所示分别表示这件衣服可干洗，不可漂白，应低温熨烫或悬挂凉干，它们其中是轴对称图形的是（）15．如图，在四个图形中，对称轴条数最多的一个图形是（）A．B．C．D．16．在直角坐标系中，点P（2,1）关于x轴对称点的坐标是（）A．（2,1）B．（－2,1）C．（2，－1）D（－2，－1）17．将一圆形纸片对折后再对折，得到如图所示的图形，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是（）18．王明是班上公认的“小马虎”在做作业时，将点A的纵横坐标次序颠倒，写成A（a，b）,小华也不细心，将点B的坐标写成关于y轴的对称点的坐标，写成B（－b，－a），则A、B两点原来的位置关系是（）A．关于y轴对称B．关于x轴对称C．A和B重合D．以上都不对三、解答题（共46分）19．（7分）如图所示，下面两个图形关于某条直线对称，画出其对称轴，求出zyx,,的值．20．（7分）如图是由两个等边三角形组成的图形，它是轴对称图形吗？如果不是，请移动其中的一个三角形，使它与另一个三角形一起组成轴对称图形，有几种移法？（至少画四种，相同类型的算一种）．21．（8分）你能将方格中的图案做如下变换吗？相信你一定能行的！（1）关于x轴对称；（2）关于y轴对称22．（8分）AC、AB是两条笔直的交叉公路，M、N是两个实习点的同学参加劳动，现欲建一个茶水供应中，使得此茶水供应站到公路两边的距离相等，且离M、N两个实习点的距离也相等，试问：此茶水供应站应建在何处？23．（8分）已知A（2m+n，2）、B（1，n－m），当m，n分别为何值时（1）A、B关于x轴对称；（2）A、B关于y轴对称．24．（8分）开放与探究（1）观察图中①－④中阴影部分所构成的图案，请写出这四个图案都具有的两个特征；（2）借助图中⑤的网格，请你设计一个新图案，使该图案同时具有你解答（1）中所写的两个共同的特征．参考答案CBA（第13题）（第17题）（§11.1～11.2）一、填空题1．80，13 2．是 不是 3．全等三角形，≌ 4．AC =BD ，AB =BA ，∠C =∠D ，∠CAB =∠DBA ，∠ABC =∠BAD 5．60度 6．90 7．ADF BCE △≌△，得F E ∠=∠． 8．∠AOC =∠BOD ，OC =OD ，△BOD 9．1，有两边及其夹角对应相等的两个三角形全等10．此工具是根据三角形全等制作而成的．由O 是AA '，BB '的中点，可得AO A O '=，BO B O '=，又由于AOB ∠与A OB ''∠是对顶角，可知AOB A OB ''∠=∠，于是根据“SAS ”有AOB A OB ''△≌△，从而A B AB ''=，只要量出A B ''的长度，就可以知道工作的内径AB 是否符合标准 二、选择题11．A 12．Ｄ 13．C 14．A 15．B 16．D 17．A 18．C 三、解答题19．（1）和（10），（2）和（12），（4）和（8），（5）和（9）是全等图形 20．略 21．略 22．由△ABF ≌△,DCE 可得到BAF CDE AFB DEC ABF DCE AB DC BF CE AF DE ∠=∠∠=∠∠=∠===，，，，，；A F E D A CB D B FC =∥，，∥，△AEC ≌△DFB 等 23．略 24．（1）证明Rt △CDE ≌Rt △AFB ；（2）DF ∥BE 且DF=BE（§11.3）一、填空题1．这个角的平分线上 2．1.5cm 3．30° 4．8 5．MN ⊥PQ 6．三条角平分线 7．6cm 8．到角的两边的距离相等 9．（1）=（2）= 10．135 二、选择题11． D 12． B 13．D 14．D 15．B 16．C 17．D 18．A 三、解答题19．50° 20．画两个角的角平分线的交点P 21．略 22．提示：过点D 做DM ⊥BC 23．①略；②锐角三角形 24．提示：过P 作三边AB 、AC 、BC 的垂线段PD 、PE 、PF（§12.1～12.2）一、填空题1．轴对称图形，5 2．答案不唯一如：“美、善、口、工、士”等 3．4 4．互相重合，轴对称图形，对称轴，成轴 5．1021∶ 6．（2,1），（－2，－1） 7．（2，－3） 8．（－2，1.5）、（－2，－1.5）、（2，－1.5） 9．60° 10．）（），，（3-1.3-1-N M二、选择题11．B12．B13．C14．B15．B16．C17．C 18．B 三、解答题19．对称轴为MN，2,6,70==︒=zyx20．不是，答案不唯一21．略22．图略，画法：（1）画出∠CAB的角平分线AE；（2）连结MN，作MN的垂直平分线与AE交于P；（3）由点P即为所求23．（1）m=1,n=－1，点A、B关于x轴对称；（2）m=－1,n=1，点A、B关于y轴对称．24．答案不唯一：如（1）都是轴对称图形；阴影部分面积等于4个小正方形面积之和；（2）答案不唯一．（§12.3）一、填空题1．35 2．15 3．80°4．36°5．②6．7或11 7．36 8．线段中垂线9．)0,41(，5 10．5或4二、选择题11．B 12．D 13．D 14．D 15．B 16．D 17．D 18．C三、解答题19．⊿ABC，⊿ADB，⊿ADC ，∠B=36°20．EF=8㎝21．（1）利用角平分线性质得PC=PD，所以∠PCD=∠PDC （2）成立22．略23．略24．15°（§13.1～13.2）一、填空题1．14.14 0.1414 2．< 3．4 4．-3，13，3 5．±5 6．-1.5 7．3m8．-6，-0.008 9．4 10．2，3或-3二、选择题11．C 12．D 13．B 14．A 15．D 16．C 17．C 18．C 三、解答题19．⑴15 ⑵-0.02 ⑶72±⑷-0.1 ⑸0.7 ⑹9 20．⑴0.01 0.1 1 10 100；⑵被开方数小数点向左（或右）移动三位，它的立方根的小数点向左（或右）移动一位；⑶①14.42 0.144221．⑴-2 ⑵0.4 ⑶25-⑷9 22．（1）x=-3；（2）x=1 2324．±10（§13.3）一、填空题1．5，54 3．34或344．22-+5．一一对应6．0 、1、-17．＜8．9．3+310．6二、选择题11．C 12．D 13．A 14．B 15．C 16．D 17．C 18．B 三、解答题19．整数{30-；分数：220.3 1.7327⎧⎫-⎨⎬⎩⎭，，；正分22300100017⎫⎬⎭，，20．C，(D21．（1）-（2）122．（1）65x=±；（2）0x= 23．325-24．2期中复习一、填空题1．23±，0.6 2．0和1，1±和0 3．2 4．30度5．12x6．Z 7．3 8．1.4π-9．1 10．（2，0）二、选择题11．A 12．D 13．D 14．B 15．B 16．B 三、解答题17．略18．（1（2）5219．（1）2；（2）2-20．1.58 21．450米22．36度，72度，72度23．略24．略25．略26．略27．28．（1）可行；（2）可行；（3）构造三角形全等，可以．期中测试一、填空题1．千分位2．0或6-3．3 415．42,3±-6．15 7．90度8．AB、BC 9．B E∠=∠（答案不唯一）10．65二、选择题11．D 12．D 13．D 14．B 15．C 16．B 三、解答题17．（1）1-（2118．略19．能20．（1）略；（2）DE=DC 21．0.8cm 22．略23．32cm24．略25．（1）111n n-+；（2）①20072008，②1nn+；（3）1003401626．略27．（1）211n+=+；（2）10OA =；（3）554 28．（1）45度；（2）会；（3）2BAC DAE ∠=∠．（§14.1～14.2）一、填空题1．3y x =- 2．25x ≥3．2 4．1,2- 5．（3，0）（0，1） 6．y=30x ，30；x 、y 7．y=1.8x-6 8．2x ≥9．S=3n －3 10．图象法；二、选择题11．C 12．C 13．D 14．C 15．C 16．D 17．C 18．C 三、解答题19．y= —2x+35（0＜x ＜9.5） 20．C 4H 10 m=2n+2 21．（1）距离；时间，900m （2）20分，45分；（3）在商场；（4）45米/分，60米/分 22．（1）①0.2②0.1t-0.1；（2）图象略；（3）当0<t<3时，y=0.2，当4<t ≤5时，y=0.4（§14.3）一、填空题1．4x =- 2．22y x =-+，1<，1> 3．24y x =-+，243y x =- 4．(20)，，(04)， 5．(13)--，，1-，3-，221x y x y -=⎧⎨-=⎩，6．6 7．1x =-，1x <- 8．3- 9．平行，没有，无解10．103m <≤二、选择题11．C 12．A 13．D 14．A 15．A 16．A 17．B 18．C 三、解答题19．（1）当173x =时，0y =；（2）当5x =时，2y =-；（3）当7x =时，4y =20．（1）当95x =时，0y =；（2）当95x <时，0y <；（3）略 21．图略，解为523.2x y ⎧=⎪⎪⎨⎪=⎪⎩， 22．142.a b =⎧⎨=⎩，23．（1）每月行驶路程小于1500千米，租国营公司的车合算；（2）每月行驶路程等于1500千米，租两家车的费用相同；（3）由图象可知租个体车主的车合算 24．（1）41k -<<；（2）直线26x y -=与y 轴的交点为(03)-，，直线31x y +=与y 轴的交点为103⎛⎫ ⎪⎝⎭，，它们的交点为(41)-，，112043233S ⎛⎫=⨯⨯+=⎪⎝⎭△ （§15.1～15.2）一、填空题1．2009 2．2242a b ab -+、12a - 3．18 4．214a - 5．16610⨯ 6．()ab a b a a 2222+=+ 7．1 8．32231638a b a b -- 9．2、3、1 10．6 二、选择题11．D 12．A 13．B 14．C 15．B 16．C 17．D 18．D 三、解答题19．（1）9a 2—b 2；（2）1002001 20．10x 21．22427a b +，19 22．x =3 23．2ab ac bc c --+24．能，35551113243=；4441114256=；3331115125=．因为256243>>，所以111111256243125>>．所以444555333435>>．（§15.3）一、填空题1．67)(,m a a - 2．36n ，41052⨯ 3．xy x y 44323-+- 4．323b a 5．21n n +6．20085,a x 7．m ＝－3 8．1 9．92 10．1cm二、选择题11．C 12．A 13．C 14．D 15．C 16．A 17．C 18．D 三、解答题19．（1）24a b ；（2）22473ab b a a +- 20．x y -，1.5 21．（1）yx -221；（2）小亮不能报出一个整式 22．3222x x x ++ 23．±2x 2y 24．（1）9610,10；（2）181210,10；（3）不相等期末复习一、填空题1．2,2±- 2．（2，1） 3．2 4．对称5．无数，直径所在的直线 6．y=-3x7．±2 8．x ＞-2 9．60 10．4或-203 二、选择题11．D 12．C 13．D 14．B 15．B 16．A 三、解答题17．1 18．- 19．29 20．72-21．（1）2(4)(4)m m m +-；（2）()()()x y a b a b -+- 22．（1）52-；（2）-5 23．略 24．（1）3y x =-+；（2）6 25．（1） 1.832y x =+26．略 27．（1（21 28．略期末测试一、填空题1．（1，2） 2．3326,61x y x x -+- 3．23(2)x x y - 4．6- 5．12± 6．三 7．68．111n n n n n n ++=++ 9．1 10．11n x +-二、选择题11．D 12．C 13．D 14．D 15．A 16．C 三、解答题17．（1）3523-+a a （2）xy 20- （3）ab 18．（1）)2(222b ab a a +-；（2）))()((22y x y x y x -++；（3）2)32(y x + 19．73-20．①23；②21 21．略 22．ab π 23．78 24．（1） 1.5 4.5y x =+；（2）21cm 25．略 26．略 27．（1）34k =；（2）9184s x =+（-8＜x ＜0）；（3）P （139,28-） 28．（1）l 1；（2）B 的速度快；（3）15分钟不能追上A ；（4）B 一定能追上A ；（5）B 能在A 逃入公海前追上。