【数学】黑龙江省大庆实验中学2017-2018学年高一下学期期中考试试题(理)(附答案)

黑龙江省大庆实验中学2017—2018学年度下学期期中考试高一物理试题一、选择题（本题共14小题，每小题4分，共56分．在每小题给出的四个选项中，1-9小题只有一个选项正确，10-14小题有多个选项正确.全部选对的得4分，选不全的得2分，有选错或不选的得0分．）1.下列关于万有引力的说法正确的是（）A.牛顿测出了万有引力常量GB. 对于质量分布均匀的球体，公式F=G中的r指两球心之间的距离C. 因地球质量远小于太阳质量，故太阳对地球的引力远小于地球对太阳的引力D. 只有当物体的质量大到一定程度时，物体之间才有万有引力2.关于曲线运动下列叙述正确的是（）A. 物体受到恒定外力作用时，就一定不能做曲线运动B. 物体只有受到一个方向不断改变的力，才可能做曲线运动C. 物体受到不平行于初速度方向的外力作用时，就做曲线运动D. 平抛运动不是匀变速曲线运动3.如图所示，木块M可以分别从固定斜面的顶端沿左边或右边由静止开始滑下，且滑到A点或B点停下．假定木块M和斜面及水平面间有相同的动摩擦因数，斜面与平面平缓连接，图中O点位于斜面顶点正下方，则（）A. 距离OA等于OBB. 距离OA大于OBC. 距离OA小于OBD. 无法做出明确的判断4.如图所示，固定的倾斜光滑杆上套有一个质量为m的圆环，圆环与竖直放置的轻质弹簧一端相连，弹簧的另一端固定在地面上的A点，开始弹簧处于原长h，让圆环沿杆滑下，圆环滑到杆的底端时速度恰好为零，则在圆环下滑过程中（）A. 圆环机械能守恒B. 弹簧的弹性势能先增大后减小C. 当圆环的动能最大时弹簧的弹性势能最大D. 当圆环滑到杆的底端时弹簧的弹性势能为mgh5.如图所示，在倾角为θ的固定斜面顶端A以初速度v0水平抛出一个可视为质点的小球，小球最后落在斜面上的B点．从小球运动轨迹上离斜面最远处的C点作斜面的垂线，与斜面的交点为D，且CD=H，AD=x1，BD=x2，不计空阻力，下列说法正确的是（）A. 一定有x1＞x2B. 一定有x1＜x2C. x1、x2的大小关系与v0有关D. x1、x2的大小关系与H有关6.如图所示为赛车场的一个水平“梨形”赛道，两个弯道分别为半径R=90m的大圆弧和r=40m的小圆弧，直道与弯道相切。

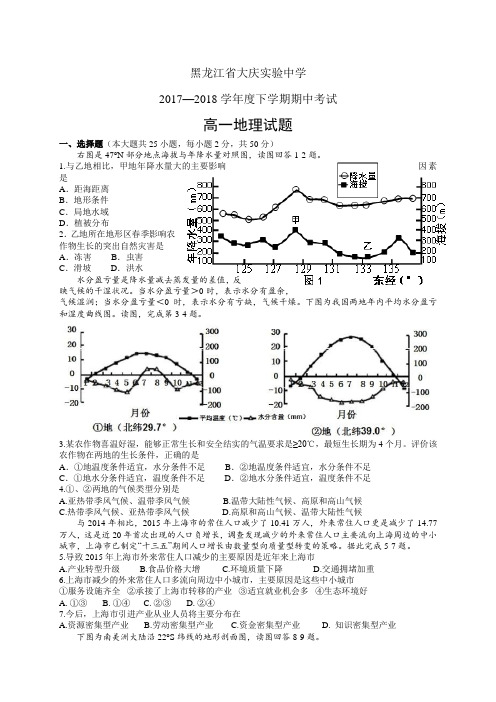
黑龙江省大庆实验中学2017—2018学年度下学期期中考试高一地理试题一、选择题（本大题共25小题，每小题2分，共50分）右图是47°N部分地点海拔与年降水量对照图，读图回答1-2题。

1.与乙地相比，甲地年降水量大的主要影响因素是A．距海距离B．地形条件C．局地水域D．植被分布2．乙地所在地形区春季影响农作物生长的突出自然灾害是A．冻害B．虫害C．滑坡D．洪水水分盈亏量是降水量减去蒸发量的差值，反映气候的干湿状况。

当水分盈亏量＞0时，表示水分有盈余，气候湿润；当水分盈亏量＜0时，表示水分有亏缺，气候干燥。

下图为我国两地年内平均水分盈亏和湿度曲线图。

读图，完成第3-4题。

3.某农作物喜温好湿，能够正常生长和安全结实的气温要求是≥20℃，最短生长期为4个月。

评价该农作物在两地的生长条件，正确的是A．①地温度条件适宜，水分条件不足B．②地温度条件适宜，水分条件不足C．①地水分条件适宜，温度条件不足D．②地水分条件适宜，温度条件不足4.①、②两地的气候类型分别是A.亚热带季风气候、温带季风气候B.温带大陆性气候、高原和高山气候C.热带季风气候、亚热带季风气候D.高原和高山气候、温带大陆性气候与2014年相比，2015年上海市的常住人口减少了10.41万人，外来常住人口更是减少了14.77万人，这是近20年首次出现的人口负增长，调查发现减少的外来常住人口主要流向上海周边的中小城市，上海市已制定“十三五”期间人口增长由数量型向质量型转变的策略。

据此完成5-7题。

5.导致2015年上海市外来常住人口减少的主要原因是近年来上海市A.产业转型升级B.食品价格大增C.环境质量下降D.交通拥堵加重6.上海市减少的外来常住人口多流向周边中小城市，主要原因是这些中小城市①服务设施齐全②承接了上海市转移的产业③适宜就业机会多④生态环境好A. ①③B. ①④C. ②③D. ②④7.今后，上海市引进产业从业人员将主要分布在A.资源密集型产业B.劳动密集型产业C.资金密集型产业D. 知识密集型产业下图为南美洲大陆沿22°S纬线的地形剖面图，读图回答8-9题。

大庆实验中学2017-2018学年度下学期六月份月考理科高一数学试题一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知非零实数满足，则下列不等式一定成立的是 ( )A. B. C. D.【答案】A【解析】分析：由非零实数满足，利用函数的单调性和不等式的性质，即可求解.详解：由题意，非零实数满足，①中，根据不等式的性质，可得是正确的；②中，例如当时，满足，但是不成立的；③中，当时，满足，此时，所以不一定成立；④中，因为的对数为单调递减函数，所以，所以不正确，故选A.点睛：本题主要考查了比较大小问题，其中熟记指数函数的单调性和不等式的基本性质是解答的关键，着重考查了推理与论证能力，属于基础题.2. 设是两个不同的平面，是两条不同的直线，且，则下列说法正确的是（）A. 若，则B. 若，则C. 若，则D. 若，则【答案】C【解析】分析：根据线面位置关系的判定和性质，逐一判定，即可得到结论. 详解：对于A 中，若，则或相交，不正确；对于B 中，若，则的位置关系可能相交、平行或异面，所以不正确；对于C 中，根据平面与平面垂直的判定，可知是正确的； 对于D 中，若，则的位置关系可能相交、平行或异面，所以不正确，故选C.点睛：本题主要考查了空间中点、线、面的位置关系的判定，其中熟记线面位置关系的判定定理和性质定理是解答此类问题的关键，着重考查了推理与论证能力，属于基础题. 3. 直线的倾斜角的取值范围是 ( )A.B.C.D.【答案】B【解析】分析：根据题意，求出直线的斜率，再根据斜率与倾斜角的关系，即可求解倾斜角的取值范围. 详解：根据题意，直线的斜率为，则，设直线的倾斜角为，则，即，所以，即直线的倾斜角为，故选B. 点睛：本题主要考查了直线的倾斜角的求解，其中根据直线方程求得直线的斜率，再利用倾斜角与斜率的关系求解是解答的关键，着重考查了推理与计算能力.4. 圆心在直线上的圆与轴交于两点，，则圆的方程为 （ ）A.B.C. D.【答案】A【解析】分析：根据题意，确定圆的圆心坐标，然后利用两点间的距离公式求得圆心到点的距离，即为圆的半径，即可得的圆的标准方程.详解：根据圆的垂径定理可得的垂直平分线过圆心，而圆心过，则圆心坐标为，又由，所以所求圆的标准方程为，故选A.点睛：本题主要考查了圆的标准方程的求解，其中熟记圆的垂径定理和两点间的距离公式求解圆的圆心坐标和圆的半径是解答的关键，着重考查了推理与运算能力.5. 若，满足约束条件，则的最小值为（）A. B. C. 0 D. 1【答案】B【解析】分析：作出不等式组对应的平面区域，利用目标函数的几何意义，即可求解目标函数的最小值.详解：作出不等式组所表示的平面区域，如图所示，由，则，结合图象可知，平移直线经过点时，直线的截距最大，此时取得最小值，由，解得，所以目标函数的最小值为，故选B.点睛：本题主要考查了利用线性规划求最小值问题，其中正确作出不等式组所表示的平面区域，利用目标函数的几何意义，结合数形结合的数学思想解答是求解的关键，着重考查了数形结合思想和推理、运算能力.6. 如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为 ( )A. B. C. D.【答案】B【解析】由三视图可得，直观图为一个完整的圆柱减去一个高为6的圆柱的一半，V=π•32×10﹣•π•32×6=63π，故选B．点睛：本题的难点在于找到三视图对应的原几何体，本题只能靠直接观察和尝试，才能找到原几何体.7. 若直线互相平行，则实数=（）A. 1B. 2C.D. 或2【答案】C【解析】分析：根据两直线平行斜率相等的性质列方程求解即可.详解：两直线，互相平行，若，符合题意；若，又知时，与重合，不合题意，所以实数的值为，故选C.点睛：本题主要考查直线的方程，两条直线平行与斜率的关系，属于简单题. 对直线位置关系的考查是热点命题方向之一，这类问题以简单题为主，主要考查两直线垂直与两直线平行两种特殊关系：在斜率存在的前提下，（1）；（2），这类问题尽管简单却容易出错，特别是容易遗忘斜率不存在的情况，这一点一定不能掉以轻心.8. 等差数列的首项为1，公差不为0．若a2，a3，a6成等比数列，则前6项的和为( )A. 8B.C. 3D.【答案】D【解析】分析：利用等差数列的通项同时，等比数列的性质列出方程，求出公差，由此能求出数列的前项和.详解：因为等差数列的首项为1，公差不为0，且成等比数列，所以，即，所以，解得，所以数列的前6项和为，故选D.点睛：本题主要考查了等差数列的前和的求解，其中解答中涉及到等差数列的基本量的运算和等比数列的性质，解题是要认真审题，注意等差数列、等比数列性质的综合运用，着重考查了推理与运算能力.9. 是边长为2的等边三角形，为中点，以为折痕，将折成直二面角，则过四点的球的表面积为（）A. B. C. D.【答案】C【解析】由题意，知过四点的球的直径为以为邻边的长方体的对角线的长，而，则，所以球的表面积为，故正确答案为C.点睛：此题主要考查了从平面图形到空间几何体的变化过程的空间想象能力，简单组合体中直三棱锥与外接球关系，以及球的表面积的计算等方面的知识和技能力，属于中档题型，也是常考题型.在解决简单几何体的外接球问题中，一般情况下，球的直径为简单几何体的对角线的长.10. 如图，三棱锥中，，，点分别是的中点，则异面直线，所成的角的余弦值是（）A. B. C. D.【答案】D【解析】分析：连接，取的中点，连接，推导出异面直线所成的角就是，通过解三角形，即可得到答案.详解：连接，取的中点，连接，则，所以是异面直线所成的角，因为，所以，又，所以，所以，故选D.点睛：本题主要考查了空间中异面直线所成角的求解，其中解答中把异面直线所成的角转化为相交直线所成的角是解答此类问题的关键，着重考查了空间思维能力，以及推理与计算能力，属于中档试题.11. 如图，在正方体中，点在线段上运动，则下列判断中不正确的是（）A. 与所成角的范围是B.C.D. 三棱锥的体积不变【答案】A【解析】分析：利用正方形的性质和线面位置关系，以及三棱锥的体积转化等知识点，逐一判定，即可得到答案.详解：对于A中，当点与线段的两端点重合时，与所成的角的最小值为，当点与线段的中点重合时，与所成的角的最小值为，故与所成的角的取值范围是，所以是错误的；B中，连接容易证明平面平面，从而由线面平行的定义可得平面，所以是正确的；C中，连接，根据正方体的性质，有平面，平面，从而可证得平面平面，所以是正确的；D中，因为，则到平面的距离不变，且三角形的面积不变，所以是正确的，综上可知，错误的应为A，故选A.点睛：本题主要考查了正方体的性质的应用，以及点线面的位置关系的判定与锥体的体积的应用等知识点的综合考查，解答中认真审题，把握好空间中的线面位置关系的判定是解答的关键，着重考查了空间思维能力，以及推理与论证能力.12. 满足条件的三角形的面积的最大值是 ( )A. B. C. D.【答案】D【解析】分析：设，根据三角形的面积公式和余弦定理，得出关于的面积表达式，再根据的取值范围，即可求解面积的最大值.详解：设，则，根据面积公式得，根据余弦定理得，代入上式，得，由三角形的三边关系可得，解得，故点时，取得最大值，故选D.点睛：本题主要考查了正弦定理、余弦定理和三角形的面积公式在解三角形中的应用，当设计到与三角形有关的最值问题时，可考虑利用正弦、余弦定理转化为函数，利用函数的单调性求解，着重考查了分析问题和解答问题的能力，以及推理与运算能力，属于中档试题.二．填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上.13. 的内角的对边分别为，【答案】【解析】分析：已知等式利用正弦定理化简，整理得到关系式，再利用余弦定理表示出，把得出关系式代入的值，即可得到答案.详解：因为，利用正弦定理化简可得，即，所以，所以.点睛：本题主要考查了正弦定理和余弦在解三角形中的应用，在解有关三角形的题目时，要有意识地考虑用哪个定理更合适，或是两个定理都要用，要抓住能够利用某个定理的信息．一般地，如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理；以上特征都不明显时，则要考虑两个定理都有可能用到．14. 已知，则数列的前5项和为________.【答案】【解析】分析：利用列项法得到，然后求得数列的前5项和.详解：由数列的通项公式，可得，所以数列前5项和.点睛：本题主要考查了数列的求和问题，其中把数列的通项公式，裂项得到是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.15. 的最小值是________．【答案】9【解析】分析：利用同角三角函数的基本关系式化简函数的解析式，再利用基本不等式求得它的最小值即可. 详解：由题意，因为，所以，当且仅当时，即等号成立，所以最小值为.点睛：本题主要考查了三角函数的基本关系式的应用，以及基本不等式求解最值的应用，其中解答中根据三角函数的基本关系式，化简得出基本不等式的应用形式是解答的关键，着重考查了分析问题和解答问题的能力，以及推理与论证能力，属于中档试题.16. a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：①当直线AB与a成60°角时，AB与b成30°角；②当直线AB与a成60°角时，AB与b成60°角；③直线AB与a所成角的最小值为45°；④直线AB与a所成角的最大值为60°.其中正确的是________.（填写所有正确结论的编号）【答案】②③由图可知③正确；很明显，可以满足平面ABC⊥直线a，则直线与所成角的最大值为90°，④错误.故正确的是②③.【名师点睛】（1）平移直线法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面问题化归为共面问题来解决，具体步骤如下：①平移：平移异面直线中的一条或两条，作出异面直线所成的角；②认定：证明作出的角就是所求异面直线所成的角；③计算：求该角的值，常利用解三角形；④取舍：由异面直线所成的角的取值范围是，可知当求出的角为钝角时，应取它的补角作为两条异面直线所成的角.（2）求异面直线所成的角要特别注意异面直线之间所成角的范围.三．解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.17. 设是正项等比数列的前项和为，且（1）求数列的通项公式；（2）已知【答案】（1）（2）【解析】分析：（1）设等比数列的首项为，公比为，根据题意求得，即可得到等比数列的通项公式；（2）由(1)可得，利用乘公比错位相减法，即可求解数列的和.详解：；点睛：本题主要考查了等比数列的通项的公式的求解，以及“乘公比错位相减法”求和的应用，其中熟记数列的基本量的运算和求和的方法是解答此类问题的关键，着重考查了推理与计算能力.18. 的内角A，B，C的对边分别为a，b，c.已知.（1）求角C；（2）若，，求的周长.【答案】（1）（2）【解析】试题分析：（1）根据正弦定理把化成，利用和角公式可得从而求的角；（2）根据三角形的面积和角的值求得，由余弦定理求得边得到的周长.试题解析：（1）由已知可得（2）又，的周长为考点：正余弦定理解三角形.视频19. 如图所示的几何体中，四边形是正方形，【答案】（1）见解析（2）【解析】分析：（1）取的中点，连接，证得，又由是的中点，得到，进而证得，再由线面平行的判定定理，即可证得结论.（2）取的中点，连接，得到平面，得到为与平面所成的角，即可求解线面角的大小.详解：（1）取BC中点M，MF//CB,DE//CB,所以MF//DE，又MF=DE，所以四边形DEFM为平行四边形（2）点睛：本题主要考查了线面平行的证明，以及直线与平面所成角的求解，其中熟记线面平行的判定定理和直线与平面所成角的定义是解答的关键，着重考查了推理与论证能力.20. 设的内角A，B，C的对边分别为a，b，c，，且B为钝角,(1)；（2）求的取值范围【答案】（1）B=+A.（2）（，]【解析】分析：（I）由题意及正弦定理，得，进而得，即可求解；详解：（I）由a=btanA及正弦定理，得,所以sinB=cosA，即 sinB=sin（+A）.又B为钝角，因此+A（，A），故B=+A.(II)由（I）知，C=-（A+B）=-(2A+)=-2A>0，所以A，于是sinA+sinC=sinA+sin（-2A）= sinA+cos2A=-2A+sinA+1=-2（sinA-）+因为0<A<,所以0<sinA<,因此由此可知sinA+sinC的取值范围是（，]点睛：本题主要考查了三角恒等变换的应用，以及利用正弦定理解三角形的应用，其中把转化为关于的函数是解答的关键，着重考查了分析问题和解答问题的能力，以及推理与计算能力.21. 如图,四棱锥中, 底面为正方形，侧棱,且，点是线段的中点，连结.(I)证明：；(II)求二面角的大小.【答案】（1）见解析（2）【解析】分析：（1）由题意，可得，又由题意可知证得，进而得到平面，利用面面垂直的判定定理，即可证得结论.（2）由（1）知平面，过作，得到，得出为二面角的平面角，即可在求解.详解：点睛：本题主要考查了平面与平面垂直的判定，以及二面角的求解问题，其中数据线面位置关系的判定与性质，以及找出二面角的平面角是解答的关键，着重考查了考生的空间思维能力，以及推理与论证能力，属于中档试题.22. 已知数列的前项和为，且（1）求数列的通项公式；（2）设，是否存在最大的正整数k，使得对于任意的正整数n，有恒成立？若存在，求出k的值；若不存在，说明理由.【答案】（1）（2）5【解析】分析：（1）由已知，则，两式相减化简得，得到数列是首项为，公比为的等比数列，即求解其通项公式；（2）由（1）可得，进而求解，利用，得出其单调性，即可求解实数的值.详解：（Ⅰ）由已知……①得……②②－①，得∴∴∴所以数列是一个以2为首项，2为公比的等比数列∴（2）∴∴∵n是正整数，∴∴数列{T n}是一个单调递增数列，又∴，要使恒成立，则又k是正整数，故存在最大正整数 k=5使恒成立点睛：本题主要考查了等比数列的通项公式的求解，以及数列的求和和数列的性质的应用，其中熟记数列的基本公式和基本量的运算，以及合理应用数列的单调性质解答本题的关键，着重考查了分析问题和解答问题的能力，以及转化的思想方法的应用，试题有一定的难度，属于中档试题.。

2017-2018学年黑龙江省大庆实验中学高一（下）4月月考数学试卷（理科）一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）如果a＜b＜0，那么下列各式一定成立的是（）A．a﹣b＞0B．ac＜bc C．a2＞b2D．＜2．（5分）设数列{a n}是等差数列，若a2+a4+a6＝12，则a1+a2+…+a7等于（）A．14B．21C．28D．353．（5分）已知△ABC内角A，B，C的对边分别为a，b，c，a＝，b＝，B＝60°，则角A等于（）A．30°B．45°C．60°D．90°4．（5分）在△ABC中，角A，B，C所对的边分别为a，b，c，S表示△ABC的面积，若S ＝，则∠A＝（）A．90°B．60°C．45°D．30°5．（5分）各项为正数的等比数列{a n}中，a5与a15的等比中项为2，则log2a4+log2a16＝（）A．4B．3C．2D．16．（5分）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高是60m，则河流的宽度BC等于（）A．m B．m C．m D．m 7．（5分）己知a，b均为正实数，函数y＝ae x+b的图象过点（0，1），则的最小值为（）A．2B．3C．4D．58．（5分）在△ABC中，若sin2A＝sin B sin C，且（b+c﹣a）（b+c+a）＝3bc，则该三角形的形状是（）A．直角三角形B．钝角三角形C．等腰三角形D．等边三角形9．（5分）设S n是等差数列{a n}的前n项和，若S4＝2，S8＝10，则S12等于（）A．12B．18C．24D．4210．（5分）下列函数的最小值为2的是（）A．y＝x+B．y＝tan x+（0＜x＜）C．y＝D．y＝sin x+（0＜x＜）11．（5分）已知{a n}满足a n+1＝a n+2n，且a1＝32，则的最小值为（）A．8﹣1B．C．D．1012．（5分）已知△ABC中，sin A，sin B，sin C成等比数列，则的取值范围是（）A．（2，]B．（0，]C．（2，+∞）D．[2，+∞）二．填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上.13．（5分）已知△ABC中，3a2﹣2ab+3b2﹣3c2＝0，则cos C＝．14．（5分）函数f（x）＝x﹣（x＞1）的最小值是．15．（5分）数列{a n}的前n项和为S n，已知a1＝，且对任意正整数mn都有a m+n＝a m•a n．若S n＜t恒成立，则实数t的最小值为．16．（5分）在△ABC中，已知，sin B＝cos A•sin C，S△ABC＝6，P为线段AB上的点，且，则xy的最大值为．三．解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤. 17．（10分）设S n是数列{a n}的前n项和，已知S n＝2a n﹣2（1）求数列{a n}的通项公式；（2）设b n＝，求数列{b n}的前n项和T n18．（12分）在△ABC中，角A，B，C所对的边分别为a，b，c，已知cos C+（cos A﹣sin A）cos B＝0．（1）求角B的大小；（2）若a+c＝1，求b的取值范围．19．（12分）已知数列{a n}满足a1＝1，a n+1＝3a n+1（1）证明{a n+}是等比数列，并求数列{a n}的通项公式；（2）设b n＝2na n，求数列{b n}的前n项和S n20．（12分）在△ABC中，角A，B，C的对边分别为a，b，c，，，且．（1）求锐角B的大小；（2）若b＝2，求△ABC面积的最大值．21．（12分）已知数列{a n}的前n项和为S n，且a1＝．（1）求{a n}的通项公式；（2）设b n＝n（2﹣S n），n∈N*，若b n≤λ，n∈N*恒成立，求实数λ的取值范围．22．（12分）在△ABC中，内角A、B、C的对边分别为a、b、c，中线AD＝m，满足a2+2bc ＝4m2．（Ⅰ）求∠BAC；（Ⅱ）若a＝2，求△ABC的周长的取值范围．2017-2018学年黑龙江省大庆实验中学高一（下）4月月考数学试卷（理科）参考答案与试题解析一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）如果a＜b＜0，那么下列各式一定成立的是（）A．a﹣b＞0B．ac＜bc C．a2＞b2D．＜【解答】解：∵a＜b＜0，∴a﹣b＜0，a+b＜0，＞，∴（a﹣b）（a+b）＝a2﹣b2＞0，即a2＞b2，故C正确，A，D不正确当c＝0时，ac＝bc，故B不一定正确，故选：C．2．（5分）设数列{a n}是等差数列，若a2+a4+a6＝12，则a1+a2+…+a7等于（）A．14B．21C．28D．35【解答】解：∵数列{a n}是等差数列，a2+a4+a6＝12，∴3a4＝12，解得a4＝4．则a1+a2+…+a7＝7a4＝28．故选：C．3．（5分）已知△ABC内角A，B，C的对边分别为a，b，c，a＝，b＝，B＝60°，则角A等于（）A．30°B．45°C．60°D．90°【解答】解：由正弦定理，，即有sin A＝＝＝，则A＝45°或135°，由于a＜b，即有A＜B＝60°，则A＝45°．故选：B．4．（5分）在△ABC中，角A，B，C所对的边分别为a，b，c，S表示△ABC的面积，若S ＝，则∠A＝（）A．90°B．60°C．45°D．30°【解答】解：由已知得：S＝bc sin A＝（b2+c2﹣a2）可得：sin A＝，由余弦定理可得：cos A＝，所以tan A＝1，又A∈（0°，180°），则A＝45°．故选：C．5．（5分）各项为正数的等比数列{a n}中，a5与a15的等比中项为2，则log2a4+log2a16＝（）A．4B．3C．2D．1【解答】解：各项为正数的等比数列{a n}中，a5与a15的等比中项为2，∴，∴＝2，∴log 2a4+log2a16＝＝＝3．故选：B．6．（5分）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高是60m，则河流的宽度BC等于（）A．m B．m C．m D．m 【解答】解：如图，∠DAB＝15°，∵tan15°＝tan（45°﹣30°）＝＝2﹣．在Rt△ADB中，又AD＝60，∴DB＝AD•tan15°＝60×（2﹣）＝120﹣60．在Rt△ADC中，∠DAC＝60°，AD＝60，∴DC＝AD•tan60°＝60．∴BC＝DC﹣DB＝60﹣（120﹣60）＝120（﹣1）（m）．∴河流的宽度BC等于120（﹣1）m．故选：B．7．（5分）己知a，b均为正实数，函数y＝ae x+b的图象过点（0，1），则的最小值为（）A．2B．3C．4D．5【解答】解：函数y＝ae x+b的图象过点（0，1），故有a+b＝1，又a，b都是正实数．∴+＝（a+b）（+）＝2++≥2+2＝4，等号当且仅当a＝b＝1时取到，即的最小值是4，故选：C．8．（5分）在△ABC中，若sin2A＝sin B sin C，且（b+c﹣a）（b+c+a）＝3bc，则该三角形的形状是（）A．直角三角形B．钝角三角形C．等腰三角形D．等边三角形【解答】解：若sin2A＝sin B•sin C，则a2＝bc．又（b+c+a）（b+c﹣a）＝3bc，∴b2+c2﹣a2＝bc，∴cos A＝＝，∴A＝60°．再根据a2＝bc以及b2+c2﹣a2＝bc，可得（b﹣c）2＝0，∴b＝c，故该三角形的形状是等边三角形，故选：D．9．（5分）设S n是等差数列{a n}的前n项和，若S4＝2，S8＝10，则S12等于（）A．12B．18C．24D．42【解答】解：∵S n是等差数列{a n}的前n项和，则S4，S8﹣S4，S12﹣S8成等差数列．∴2（S8﹣S4）＝S12﹣S8+S4，∴2（10﹣2）＝S12﹣10+2，解得S12＝24．故选：C．10．（5分）下列函数的最小值为2的是（）A．y＝x+B．y＝tan x+（0＜x＜）C．y＝D．y＝sin x+（0＜x＜）【解答】解：对于y＝x+，当x＞0时，y min＝2，排除A；∵，∴tan x＞0y＝tan x+≥2，当且仅当tan x＝即tan x＝1时取等号，故B成立；对于y＝＝≥2，当即x2+4＝1，此时x不存在，排除C；y＝2x+2﹣x＝2，当且仅当2x＝2﹣x即x＝0时取等号，故C正确；∵，∴0＜sin x＜1，y＝sin x+≥2，当且仅当sin x＝即sin2x＝1时取等号，但sin2x＝1不能成立，排除D．故选：B．11．（5分）已知{a n}满足a n+1＝a n+2n，且a1＝32，则的最小值为（）A．8﹣1B．C．D．10【解答】解：∵a1＝32，a n+1﹣a n＝2n，∴n≥2时，a n＝（a n﹣a n﹣1）+（a n﹣1﹣a n﹣2）+……+（a2﹣a1）+a1＝2（n﹣1）+2（n﹣2）+……+2×1+32＝2×+32＝n2﹣n+32，则＝n++1．令f（x）＝x++1，（x≥1）．f′（x）＝1﹣＝．可得：函数f（x）在[1，4 ）内单调递减；在（4，+∞）上单调递增．又f（5）＝6+＝＝12+，f（6）＝7+＝＝12+．∴n＝6时，则取得最小值．故选：C．12．（5分）已知△ABC中，sin A，sin B，sin C成等比数列，则的取值范围是（）A．（2，]B．（0，]C．（2，+∞）D．[2，+∞）【解答】解：△ABC中，sin A，sin B，sin C成等比数列，可得sin2B＝sin A sin C，由正弦定理可得b2＝ac，又cos B＝＝≥＝，可得0＜B≤，设t＝sin B+cos B＝sin（B+），t2＝1+2sin B cos B＝1+2sin2B，即sin2B＝t2﹣1，B+∈（，]，可得sin（B+）∈（，1]，即有t∈（1，]，由＝＝t+∈（2，]，故选：A．二．填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上.13．（5分）已知△ABC中，3a2﹣2ab+3b2﹣3c2＝0，则cos C＝．【解答】解：∵在△ABC中，3a2﹣2ab+3b2﹣3c2＝0，即a2+b2﹣c2＝ab，∴由余弦定理得cos C＝＝＝．故答案为：．14．（5分）函数f（x）＝x﹣（x＞1）的最小值是3+1．【解答】解：∵x＞1，∴2x﹣2＞0，∴f（x）＝（2x﹣2）++1≥2+1＝3+1，（当且仅当（2x﹣2）＝，即x＝时，等号成立）；故答案为：3+1．15．（5分）数列{a n}的前n项和为S n，已知a1＝，且对任意正整数mn都有a m+n＝a m•a n．若S n＜t恒成立，则实数t的最小值为．【解答】解：∵a1＝，且对任意正整数mn都有a m+n＝a m•a n，∴令m＝1，n＝1，得到a2＝a12＝，同理令m＝2，n＝1，得到a3＝a2•a1＝，∴此数列是首项为，公比为的等比数列，则S n＝＝，∵S n＜t恒成立，∴＜t，∵＝，∴t≥，∴t的最小值为．故答案为：．16．（5分）在△ABC中，已知，sin B＝cos A•sin C，S△ABC＝6，P为线段AB上的点，且，则xy的最大值为3．【解答】解：△ABC中，设AB＝c，BC＝a，AC＝b，∵sin B＝cos A•sin C，sin（A+C）＝sin C cos nA，即sin A cos C+sin C cos A＝sin C cos A．∴sin A cos C＝0，∵sin A≠0，∴cos C＝0，C＝90°．∵＝9，S△ABC＝6，∴bc cos A＝9，bc sin A＝6，∴tan A＝．根据直角三角形可得sin A＝，cos A＝，bc＝15，∴c＝5，b＝3，a＝4．以AC所在的直线为x轴，以BC所在的直线为y轴建立直角坐标系可得C（0，0），A（3，0），B（0，4）．P为线段AB上的一点，则存在实数λ使得＝λ+（1﹣λ）＝（3λ，4﹣4λ）（0≤λ≤1）．设＝，＝，则||＝||＝1，且＝（1，0），＝（0，1）．∴＝（x，0）+（0，y）＝（x，y），可得x＝3λ，y＝4﹣4λ则4x+3y ＝12，12＝4x+3y≥2，解得xy≤3，故所求的xy最大值为：3．故答案为3．三．解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤. 17．（10分）设S n是数列{a n}的前n项和，已知S n＝2a n﹣2（1）求数列{a n}的通项公式；（2）设b n＝，求数列{b n}的前n项和T n【解答】解：（1）当n＝1时，2a1＝2S1＝4a1﹣4，则a1＝2；当n≥2时，a n＝S n﹣S n﹣1＝2a n﹣2﹣2a n﹣1+2，则a n＝2a n﹣1，可得{a n}是以2为首项，2为公比的等比数列，则a n＝2n；（2）由b n＝＝＝﹣，前n项和T n＝1﹣+﹣+﹣+…+﹣＝1﹣＝．18．（12分）在△ABC中，角A，B，C所对的边分别为a，b，c，已知cos C+（cos A﹣sin A）cos B＝0．（1）求角B的大小；（2）若a+c＝1，求b的取值范围．【解答】解：（1）由已知得：﹣cos（A+B）+cos A cos B﹣sin A cos B＝0，即sin A sin B﹣sin A cos B＝0，∵sin A≠0，∴sin B﹣cos B＝0，即tan B＝，又B为三角形的内角，则B＝；（2）∵a+c＝1，即c＝1﹣a，cos B＝，∴由余弦定理得：b2＝a2+c2﹣2ac•cos B，即b2＝a2+c2﹣ac＝（a+c）2﹣3ac＝1﹣3a（1﹣a）＝3（a﹣）2+，∵0＜a＜1，∴≤b2＜1，则≤b＜1．19．（12分）已知数列{a n}满足a1＝1，a n+1＝3a n+1（1）证明{a n+}是等比数列，并求数列{a n}的通项公式；（2）设b n＝2na n，求数列{b n}的前n项和S n【解答】证明：（1）由a n+1＝3a n+1，得a n+1+＝3（a n+），又a1+＝，所以{a n+}是首项为，公比为3的等比数列．a n+＝，因此{a n}的通项公式为a n＝．（2）由（1）知b n＝2na n＝n•3n﹣n，S n＝1×31﹣1+2×32﹣2+…+n•3n﹣n，S n可以分组为S n＝（1×31+2×32+3×33+…+n•3n）﹣（1+2+3+…+n），T n＝1×31+2×32+3×33+…+n•3n，3T n＝1×32+2×33+3×34+…+n•3n+1，可得：﹣2T n＝1×31+32+33+…+3n﹣n•3n+1＝﹣n•3n+1T n＝+•3n+1，S n＝+•3n+1﹣．20．（12分）在△ABC中，角A，B，C的对边分别为a，b，c，，，且．（1）求锐角B的大小；（2）若b＝2，求△ABC面积的最大值．【解答】解：（1）在△ABC中，角A，B，C的对边分别为a，b，c，，，且，则2sin B（2cos2﹣1）＝﹣cos2B，即有2sin B cos B＝sin2B＝﹣cos2B，tan2B＝﹣，由锐角B，可得B＝；（2）由余弦定理可得，b2＝a2+c2﹣2ac cos B≥2ac﹣2ac•＝ac，可得ac≤4，当且仅当a＝c取得最大值4，则△ABC面积为S＝ac sin B≤×4×＝．即有△ABC面积的最大值为．21．（12分）已知数列{a n}的前n项和为S n，且a1＝．（1）求{a n}的通项公式；（2）设b n＝n（2﹣S n），n∈N*，若b n≤λ，n∈N*恒成立，求实数λ的取值范围．【解答】解：（1）由已知得，其中n∈N*，∴数列是公比为的等比数列，首项，∵，∴，（2）由（1）知，∴，∴，∵，∴．因此，，∴当n＝1，b2﹣b1＞0，即b2＞b1，n≥2，b n+1﹣b n＜0，即b n+1＜b n．∴b2是最大项b2＝2，∴λ≥2．22．（12分）在△ABC中，内角A、B、C的对边分别为a、b、c，中线AD＝m，满足a2+2bc ＝4m2．（Ⅰ）求∠BAC；（Ⅱ）若a＝2，求△ABC的周长的取值范围．【解答】解（Ⅰ）在△ABD和△ACD中，，因为∠ADB+∠ADC＝π，所以cos∠ADB+cos∠ADC＝0，，，由已知a2+2bc＝4m2，得a2+2bc＝2b2+2c2﹣a2，即b2+c2﹣a2＝bc，，又0＜A＜π，所以．（Ⅱ）在△ABC中有正弦定理得，又a＝2，所以，，故＝＝，因为，故，所以，b+c∈（2，4]，故△ABC周长的取值范围是（4，6]．。

大庆铁人中学高一学年下学期期中考试数学试题一、选择题（每小题只有一个选项正确，每小题 5分，共60 分。

）1. 下列说法正确的是（）A. 若，则B. 若C. 若D. 若【答案】D【解析】【分析】利用不等式的性质逐一判断每一个选项的真假.【详解】对于选项A,举例a=-2,b=1,但是，所以该选项错误；对于选项B,举例a=-2，c=-1,b=-1,满足，但是a＜b,所以该选项错误；对于选项C,举例a=-1,b=0,k=3,显然，所以该选项错误；对于选项D,由题得,所以.所以该选项正确.故答案为：D【点睛】(1)本题主要考查不等式的性质，意在考查学生对该知识的掌握水平和分析推理能力.(2)做类似的题目，可以利用不等式的性质证明，也可以举反例.2. 等差数列的前n项和为，若（）A. 11B. 9C. 13D. 15【答案】C【解析】【分析】先根据已知计算出，再利用等差数列的通项求.【详解】由题得.故答案为：C【点睛】(1)本题主要考查等差数列的前n项和，考查等差数列的通项，意在考查学生对这些知识的掌握水平和基本计算能力.(2) 等差数列的前项和公式：一般已知时，用公式，已知时，用公式3. 已知四棱锥P-ABCD（图1）的三视图如图2所示，为正三角形，PA为四棱锥P-ABCD 的高，俯视图是直角梯形，则四棱锥P-ABCD的体积（）...........................A. B. C. D.【答案】B【解析】【分析】先计算出AB,PA的长度，再求四棱锥P-ABCD的体积.【详解】由题得,所以四棱锥P-ABCD的体积为，故答案为：B【点睛】（1）本题主要考查棱锥体积的计算，意在考查学生对该知识的掌握水平.(2)求边和角，一般要解三角形.4. 在△ABC中，a，b，c分别为角A，B，C所对的边．若则A=（）A. B. C. D.【答案】C【解析】【分析】根据诱导公式和两角和的正弦公式以及正弦定理计算即可得解．【详解】sinB=sin（A+C）=sinAcosC+cosAsinC，∵b+a（sinC﹣cosC）=0，可得：sinB+sinA（sinC﹣cosC）=0，∴sinAcosC+cosAsinC+sinAsinC﹣sinAcosC=0，∴cosAsinC+sinAsinC=0，∵sinC≠0，∴cosA=﹣sinA，∴tanA=﹣1，∵＜A＜π，∴A=．故答案为：C【点睛】本题主要考查正弦定理和和角的正弦公式，意在考查学生对这些知识的掌握水平和基本计算能力.5. 已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的侧面积是（）A. B. C. D.【答案】C【解析】【分析】先求出圆柱的底面圆的半径，再求圆柱的侧面积.【详解】由题得圆柱的底面圆的半径为，所以圆柱的侧面积为.故答案为：C【点睛】（1）本题主要考查球的内接圆柱问题，意在考查学生对这些知识的掌握水平和空间想象观察能力.(2)本题解题的关键是求出圆柱的底面圆的半径.6. 设x，y满足约束条件，则的最小值是（）A. -15B. -9C. 9D. 1【答案】D【解析】【分析】先作出不等式组对应的可行域，再通过数形结合分析得到的最小值.【详解】不等式组对应的可行域如下图所示，因为z=2x+y,所以y=-2x+z,当直线经过点A时，直线的纵截距z最小，解方程组得A(0,1),所以z最小=2×0+1=1，故答案为：D【点睛】(1)本题主要考查线性规划，意在考查学生对这些知识的掌握水平和数形结合分析推理能力.(2) 解答线性规划时，要加强理解，不是纵截距最小，就最小，要看函数的解析式，如：,直线的纵截距为,所以纵截距最小时，最大.7. 一个直角梯形的一个底角为，下底长为上底长的倍，这个梯形绕下底所在直线旋转一周所形成的旋转体体积为，则该直角梯形的上底长为（）A. 2B.C.D.【答案】A【解析】【分析】由题意可知，这个几何体的体积是一个圆锥加一个同底圆柱的体积．再根据题目中的条件求解即可．【详解】如图，梯形ABCD，AB∥CD，∠A=90°，∠B=45°，绕AB边旋转一周后形成一圆柱和一圆锥的组合体．设CD=x，AB=，AD=x．∴旋转体体积V=S圆柱+S圆锥=.故答案为：A【点睛】本题主要考查圆柱和圆锥体积，考查组合体的体积，意在考查学生对这些知识的掌握水平和空间想象能力.8. 已知等比数列的各项都为正数，且为与的等差中项，则（）A. 14B. 18C. 16D. 20【答案】B【解析】【分析】根据等差中项的定义求出a6的值，结合对数的运算法则以及等比数列的运算性质进行化简即可．【详解】∵为与的等差中项,∴2a6=+=8，即a6=4，在正项等比数列中，log2a2+log2a3+…log2a10=log2（a2•a3…a9•a10）=log2（a6）9=9log24=9×2=18，故答案为：B【点睛】（1）本题主要考查等差中项，考查等比数列的性质和对数的运算，意在考查学生对这些知识的掌握水平和基本计算能力.(2) 等比数列中，如果,则,特殊地，时，则，是的等比中项.9. 已知函数的图像恒过定点A，若点A在直线上，其中，则的最小值是（）A. 9B. 4C.D. 8【答案】C【解析】【分析】先求出定点A的坐标，再代入直线的方程得到m+n=2,再利用基本不等式求最小值.【详解】由题得A(-2,-2),所以-2m-2n+4=0,所以m+n=2,所以=.当且仅当时取到最小值.故答案为：C【点睛】(1)本题主要考查对数函数的定点问题，考查基本不等式，意在考查学生对这些知识的掌握水平和分析推理计算能力.(2) 本题的解题关键是常量代换，即把化成，再利用基本不等式求函数的最小值. 利用基本不等式求最值时，要注意“一正二定三相等”，三个条件缺一不可.10. 不等式的解集为（-4,1），则不等式的解集为（）A. B. C. D.【答案】B【解析】【分析】根据不等式ax2+bx+c＞0的解集求得a、b、c的关系，代入不等式b（x2+1）﹣a（x+3）+c＞0中，化简并求出该不等式的解集可得答案．【详解】不等式ax2+bx+c＞0的解集为（﹣4，1），则不等式对应方程的实数根为﹣4和1，且a＜0；由根与系数的关系知，，∴，∴不等式b（x2+1）﹣a（x+3）+c＞0化为3a（x2+1）﹣a（x+3）﹣4a＞0，即3（x2+1）﹣（x+3）﹣4＜0，解得﹣1＜x＜，∴该不等式的解集为（﹣1，）．故答案为：B【点睛】（1）本题主要考查含参的一元二次不等式的解法，意在考查学生对这些知识的掌握水平和基本的计算能力.(2)解题的关键是由根与系数的关系知，得到.11. 在锐角中，A、B、C分别为三边a,b,c所对的角。

大庆实验中学2017-2018学年度下学期六月份月考高一数学（文）试题第Ⅰ卷(选择题共60分)一．选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若a b 0，则下列不等式中错误的是（）1111A．B． C. D．a b a2 b2a b a b a2. 直线x sin y 2 0的倾斜角的取值范围是()[0, ] A．[0， )B．[0,](,)错误！未指定书签。

C.4243D．[0,][,)443. 设m,n是两条不同的直线， , 是两个不同的平面，则下列命题中正确的是( )A．若m n,n A ，则m B．若m A , ，则mC. 若m ,n ,n ，则m D．若m n,n , ，则m4. 已知数列 为等差数列，为其前项和，若，则a S n3S S S an n32412,a 5( )A． 12B． 10 C. 10D．125. 在正方形网格中，某四面体的三视图如图所示，如果小正方形网格的边长为1，那么该四面体的体积为（）A．64B．3264C. D．332 3- 1 -x y0z 3x 4y6. 若x，y满足约束条件，则的最小值为( )x y20y0A．1B．0 C. 1D． 27. 若直线互相平行，则实数=l1:mx (m+1)y m 0与l2:(m 2)x 2(m 1)y 4 0m ( )A．1B．2 C. 1D． 1或2n 1 a8. 已知数列 为等差数列，为其前项和，，若则a1,a mS n a Sn8, n n1n m2（）A．8B．5 C. 7D．69. 设 ABC的内角A,B,C的对边分别为a,b,c，且满足B,a3,cos C cos A sin B sin B sin Cb222，则( )4A．1B．2 C. 3D．210. 在正四面体P ABC中，D,E,F分别为AB,BC,CA的中点，则下面四个结论中不成立的是（）A．平面PDE 平面ABC B．BC A平面PDFC. DF 平面PAE D．平面PAE 平面ABC11. 如图，在正方体中，点在线段上运动，则下列判断中不正确的ABCD A B C D P BC11111D C是( )A BA．平面平面PB D ACD11P B．A1P//平面ACD1C.异面直线与所成角的范围是A P AD0,113 A1D1B1C1D．三棱锥的体积不变A CD P1- 2 -12. 在 ABC中，若111，则的取值范围为( )cos Atan B tan C tan A2 2 11A．B． C. D．0,,10,,13 3 33第Ⅱ卷(非选择题共90分)二．填空题：本题共4小题，每小题5分，共20分.1413. 若0，，则 的最小值为2 sin cos2214. 点P m,n是直线x y 4 0上任意一点，O为坐标原点，则的最小值为m2 n215. 已知长方体中，，则异面直线与所ABCD A B C D AB BC 1,AA 3AD DB1111111成角的余弦值为16. 在四棱锥S ABCD中，平面SAB 平面SAD，侧面SAB是边长为3的等边三角形，底面ABCD是矩形，且BC 2，则该四棱锥外接球的表面积等于三．解答题：本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.17．(本小题满分10分)Sa n a Sn n15,39设为等差数列的前项和，已知，（1）求数列 的通项公式（2）求，并求的最小值a S Sn n n18．(本小题满分12分)已知 ABC的内角A,B,C的对边分别为a,b,c，且2cos C(a cos B b cos A) c.（1）求角C；（2）若c 7，33，求的周长.S ABCABC219．(本小题满分12分)- 3 -如图，在四棱锥P ABCD中，底面ABCD是正方形，侧面PAD 底面ABCD, E,F PC,BD分别为的中点，（1）求证：EF A平面PAD；（2）若EF PC，求证：平面PAB 平面PCDPEDCFAB20．(本小题满分12分)四棱柱中，底面为正方形，, 为ABCD A B C D ABCD112AD AA A DH 1111AD中点，且．A H BD1（1）证明；（2）求点到平面的距离．AB AA CA BD11D1C1A1B1DCHA B21．(本小题满分12分)的前项和为，且（），已知数列a n S S 2a 2n N*n n n n的通项公式；（1）求an1（2）设，，是数列的前项和，若对任意b log a Tc ncn2n n 1 22b b 1n nn n- 4 -n N*均有恒成立，求的最小值．Tn22．(本小题满分12分)已知 ABC的内角A,B,C的对边分别为a,b,c，且cos2，C b ccos A a21（1）若点M在边AC上，且cos AMB ,BM 21，求 ABM的面积7（2）若 ABC为锐角三角形，且b2 c2 a bc 2，求b c的取值范围- 5 -大庆实验中学 2017-2018学年度下学期六月份月考高一 数学（文） 参考答案123456789101112B DC BD C C A B A C B13. 914. 2 215.5 516. 817、【解析】（1）设数列的公差为 ，则ad S 3 a 1 a 2 a 3 3a 1 3d 9n27a 1 5,d 2aan的通项公式为nn（2）由1 知，a a nS1nn 2 6nn 3 92n2当n 3时， 取到最小值，最小值为S 9n注：【（1）仅看结果，对 5分 （2）必须写取等条件“当 n 3时”，缺少扣 1分】a 2 c 2b 2b 2c 2 a 2 2c 2 1 8、【解析】（1）由a cos Bb cos A abc2ac2bc2c2cos C a cos B b cos A 2c cos C ccos C12 C3 113 3 3（2）由Sab C ab ab 6sin ABC2222a b 2 c2 a b 2 71cos C 1 12ab2 62ABC5 7a b5的周长为P备注：【（1）（2）问仅看结果，结果正确即满分，每问6分】ED19、AC ABCD F AC【解析】（1）连结,则由为正方形，得是的中点FE PC为的中点AB PACEF为的中位线- 6 -EF A PA又 PA 面PAD , EF 面PADEF A 平面PAD（2）由（1）可得， EF PA由 EF PC ，PA PC 平面平面 ，平面 平面PAD ABCD PAD ABCD =AD ,CD ADCD 平面PAD CD PA又 CD PC C ,PA 面PCD又 PA 平面 PABPABPCD平面平面20、【解析】（1）为等边三角形,且为中点,A AD H AD1A H AD1又,且A H BD AD BD D1A H 面ABCD 1A H AB1又 ABCD 为正方形AD AB又 A H ADH1AB 面ADD A1 1AB AA1(2) 由题意得，在中，,A D BD A BA BD12,22,12217SA BD1- 7 -由(1)知，A H 面ABCD11123V S A H2 3A BCD BCD11333设点C到平面的距离为，则由V V 得，A BD h1C A BD A BCD111123S h h7A BD3331，则C A BD d点到平面的距离为1221721、n 1 a【解析】（1）当时，，则a1 S1 2a1 212当n 2时，a S S 1 2a 2a 1，n n n n na a2n n1a22是以为首项，为公比的等比数列nan2n（2）由1 知，，b log a ncn2n n11 11n n nn2121221211 11111T 1 ......1 111124n2n2 3352n12n1 22n111又由对任意均成立T n Nn24n 211的最小值为2222、 ABC cos2C b c【解析】（1）在中，，则由正弦定理得，cos A acos sin 2sin sin A cos C cos A sin C2sin BC C Bcos A sin A sin A cos A sin A sin Asin A C 2sin Bcos A sin A sinA，10 A cos A由得，2A32127又由cos AMB ,得sin AMB ，77- 8 -AB BM由正弦定理可知，sin AMB sinA，即AB27721sin60AB4116 AM 212，由余弦定理有，则22 4 AMA M5127S AM BMABM27532221b c a（2）由知，，得A cos b2 c2 bc a2A322bc又b2 c2 a bc 2 a2 a 2 0 a 2，a b c244 4b sin B,c sin C由正弦定理，则sin sin sin sin3A B C3 334444b c sin B sin C sin B sin B3333 34s in B6由 ABC为锐角三角形，则0,02，得B B B232624s in 23,4即的取值范围为b c 23,4b c B4s in 23,46- 9 -。

大庆实验中学2018-2019学年度下学期期中考试高一数学（理）试题第Ⅰ卷(选择题共60分)一．选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知实数，且，则以下不等式恒成立的是（）A. B. C. D.【答案】A【解析】【分析】根据幂函数的单调性判断；令，判断，根据指数函数的单调性判断．【详解】因为是增函数，所以由可得，选项正确；当，时，不成立，选项错误；因为是减函数,由可得，选项错误，，时，不成立，选项错误，故选A．【点睛】本题主要考查不等关系与不等式的性质，属于中档题．利用条件判断不等式是否成立主要从以下几个方面着手：（1）利用不等式的性质直接判断；（2）利用函数式的单调性判断；（3）利用特殊值判断.2.一元二次不等式的解集为（）A. B.C. D.【答案】C【解析】【分析】把一元二次不等式化成一般形式后再求出解集即可．【详解】原一元二次不等式化为，解得，所以不等式的解集为．故选C．【点睛】本题考查一元二次不等式的解法，解题时注意解不等式的步骤，同时要注意结合二次函数的图象求解，以增加解题的直观性，属于简单题．3.设的内角所对的边分别为，若，则（）A. B. C. D. 或【答案】B【解析】【分析】根据正弦定理求得，由大边对大角的特点可知，从而求得的大小.【详解】由正弦定理得：本题正确选项：【点睛】本题考查利用正弦定理解三角形的问题，涉及到大边对大角的性质的应用，属于基础题. 4.在等差数列中，若公差，则（）A. B. C. D.【答案】B【解析】【分析】根据等差数列的通项公式求解即可得到结果．【详解】∵等差数列中，，公差，∴．故选B．【点睛】等差数列中的计算问题都可转为基本量（首项和公差）来处理，运用公式时要注意项和项数的对应关系．本题也可求出等差数列的通项公式后再求出的值，属于简单题．5.在中，若，则（）A. B. C. D.【答案】A【解析】【分析】在三角形中运用内角和定理和两角和的正弦公式可得所求．【详解】∵在中，，∴，∴．故选A．【点睛】本题考查三角形中的三角变换问题，解题时要灵活运用三角形内角和定理得到各角间的关系，然后再借助公式求解，属于基础题．6.在等差数列中，若，则（）A. B. C. D.【答案】C【解析】【分析】根据等差数列中下标和的性质得到，从而，然后再利用前n项和公式求解即可．【详解】∵在等差数列中，，∴．∴．故选C．【点睛】利用等差数列中项的下标和的性质解题可简化运算，此性质常与等差数列的前n项和公式结合在一起考查，解题时注意整体思想的运用，属于基础题．7.已知角满足，则（）A. B. C. D.【答案】C【解析】【分析】先求出，再由两角差的正弦公式得，于是可得结果．【详解】∵，∴，∴．∴．故选C．【点睛】解答本题时要注意灵活运用三者间的关系，即知道其中的一个可以求出另外的两个，考查转化思想和计算能力，属于基础题．8.各项均为正数的等比数列的前项和为，若则（）A. B. C. D.【答案】B【解析】【分析】由，，列方程组求出，利用可得结果.【详解】设等比数列的公比为，由题意易知所以，，两式相除得，化简得，解得，所以,故选B.【点睛】本题主要考查等比数列的性质与前项和的计算，考查运算求解能力.等比数列基本量的运算是等比数列的一类基本题型，数列中的五个基本量一般可以“知二求三”，通过列方程组所求问题可以迎刃而解，解决此类问题的关键是熟练掌握等比数列的有关性质和公式，并灵活应用，在运算过程中，还应善于运用整体代换思想简化运算过程.9.在中，若，那么是（）A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定【答案】A【解析】【分析】由可得为锐角；再由得到，从而得到为锐角，所以可得三角形的形状．【详解】∵在中，，∴，∴为锐角．又，∴，∴，∴为锐角，∴为锐角三角形．故选A．【点睛】判断三角形形状的两种方法：一是根据角来判断，分为锐角、直角和钝角三角形；二是根据边来判断，分为不等边、等腰和等边三角形．解题时要注意灵活选择方法进行求解，属于基础题．10.在等差数列中，，且，为其前项和，则使的最大正整数为（）A. B. C. D.【答案】D【解析】【分析】根据条件判断出等差数列中正负项的分界点，然后再结合等差数列的前项和公式和下标和的性质求解即可．【详解】由条件得，等差数列的公差，∵，且，∴，即．∴，，∴使的最大正整数为．故选D．【点睛】解答类似问题的关键是找到数列的项或和的正负值的分界点，其中利用等差数列中项的下标和的性质和前项和的结合是解题的突破口，考查灵活运用知识解决问题和分析能力，属于中档题．11.如图，在中，点在边上，且,,,的面积为，则线段的长度为（）A.B.C.D.【答案】C【解析】【分析】先由, 的面积为，得到的面积；进而求出，再由余弦定理求出，最后在中，再根据余弦定理即可求出结果.【详解】因为, 的面积为，所以的面积为，则,即.在中，，所以，又因为，，，所以，.所以在中，，即，所以选C.【点睛】本题主要考查余弦定理解三角形，熟记余弦定理即可，属于常考题型.12.等差数列、的前项和分别为和，若，则（）A. B. C. D.【答案】D【解析】【分析】当时，可求得；进而求得，将所求式子化为，代入求得结果.【详解】由题意得：，又，即本题正确选项：【点睛】本题考查等差数列性质的应用，关键是能够利用中项的性质将问题转化为中间项之间的比较.第Ⅱ卷（非选择题共90分）二．填空题：本题共4小题，每小题5分，共20分.13.求值： __________________.【答案】【解析】【分析】利用两角和差正切公式展开，从而整理可得结果.【详解】，即本题正确结果：【点睛】本题考查利用两角和差正切公式求值问题，属于基础题.14.在等比数列中，、是关于的方程的两个实根，则____________________.【答案】【解析】【分析】根据韦达定理，结合等比数列特点可判断出等比数列的偶数项均为负数；利用求得，则，代入求得结果.【详解】由韦达定理可得：，，可知，即等比数列的偶数项均为负数，可得：又本题正确结果：【点睛】本题考查等比数列性质的应用，关键是明确等比数列的所有奇数项符号一致；所有偶数项符号一致的特点.15.已知角满足，则 __________________.【答案】【解析】【分析】运用诱导公式和二倍角余弦公式求解即可．【详解】由题意得．故答案为：．【点睛】解答三角变换中的“给值求值”问题时，要注意将所给的条件作为一个整体进行处理，把所求角根据“拼凑”的方法用已知角表示，然后进行求解，属于基础题．16.设的内角的对边分别为，点为的重心且满足向量，若，则实数________________.【答案】【解析】【分析】根据为的重心且，可得到；利用余弦定理得到，根据得到的关系；根据，通过正余弦定理化简整理，代入的关系，可求得.【详解】连接延长交于，如下图所示：为的重心为中点且又由余弦定理得：，即本题正确结果：【点睛】本题考查正弦定理、余弦定理解三角形及边角关系式的化简问题，涉及到重心的性质，解题关键是能够利用构造出边长之间的关系.三．解答题：本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.17.已知角，且，（1）求的值；（2）求的值.【答案】（1）（2）【解析】【分析】（1）根据的范围，利用同角三角函数可求得，从而构造，利用两角和差正弦公式求解得到结果；（2）根据同角三角函数求出；利用二倍角正切公式求得；根据两角和差的正切公式求得结果.【详解】（1）（2），则由（1）可知，，【点睛】本题考查同角三角函数的求解、二倍角公式的应用、两角和差的正弦和正切公式的应用问题，属于基础题.18.在中，角的对边分别为，且.（1）求角的大小；（2）若，的面积，求的值.【答案】（1）；（2）。

2017-2018学年黑龙江省大庆实验中学高一（下）期中数学试卷（理科）一．选择题（本大题共12小题，每题5分，共60分）1．（5分）已知数列{a n}是等差数列，a3=4，a7=12，则a11的值为（）A．14B．16C．18D．202．（5分）若a＜b＜0，则下列不等式不能成立的是（）A．|a|＞|b|B．a2＞ab C．D．3．（5分）下列命题中正确的是（）A．利用斜二测画法得到的正方形的直观图是正方形B．利用斜二测画法得到的平行四边形的直观图是平行四边形C．有两个面平行，其余各面都是平行四边行的几何体叫棱柱D．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台4．（5分）在△ABC中，已知三边a=3，b=5，c=7，则三角形ABC是（）A．锐角三角形B．直角三角形C．钝角三角形D．无法确定5．（5分）已知三棱锥A﹣BCD的各棱长都相等，E为BC中点，则异面直线AB 与DE所成角的余弦值为（）A．B．C．D．6．（5分）在正方体ABCD﹣A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，给出下列四个推断：①FG∥平面AA1D1D；②EF∥平面BC1D1；③FG∥平面BC1D1；④平面EFG∥平面BC1D1其中推断正确的序号是（）A．①③B．①④C．②③D．②④7．（5分）下列命题不正确的是（）A．若任意四点不共面，则其中任意三点必不共线B．若直线l上有一点在平面β外，则l在平面β外C．若一个平面内的任一条直线都平行于另一个平面，则这两个平面平行D．若直线a，b，c中，a与b共面且b与c共面，则a与c共面8．（5分）四棱锥的三视图如图所示，则最长的一条侧棱的长度是（）A．B．5C．D．29．（5分）给出以下四个命题：①若＜＜0，则+＞2；②若a＞b，则am2＞bm2；③在△ABC中，若sinA=sinB，则A=B；④任意x∈R，都有ax2﹣ax+1≥0，则0＜a≤4．其中是真命题的有（）A．①②B．②③C．①③D．③④10．（5分）已知数列{a n}的首项a1=35，且满足a n﹣a n﹣1=2n﹣1，则的最小值为（）A．2B．C．D．1211．（5分）如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，点E，F分别是棱BC，CC1的中点，P是侧面BCC1B1内一点，若A1P∥平面AEF，则线段A1P长度的取值范围是（）A．[1，]B．[，]C．[，]D．[，] 12．（5分）在△ABC中，若a2﹣c2=2b，，则b等于（）A．3B．4C．6D．7二．填空题（本大题共4小题，每小题5分，共20分）13．（5分）已知圆锥底面的半径为1，侧面展开图是一个圆心角为的扇形，则该圆锥的侧面积是．14．（5分）如图所示，为测一建筑物CD的高度，在地面上选取A，B两点，从A，B两点分别测得建筑物顶端的仰角为30°，45°，且A，B两点间的距离为20m，则该建筑物的高度为m．15．（5分）设a，b为正实数，且a+b=3，则的最小值为．16．（5分）已知数列{a n}为公差不为零的等差数列，且{a n}中的项组成的数列=1，b2=3，b3=17，则a，a，…，a，…恰为等比数列，其中bb1+b2+…+b n=．三、解答题（本大题共6小题，共70分）17．（10分）等比数列{a n}中，已知a3=8，a6=64．（1）求数列{a n}的通项公式；（2）若a4，a6分别为等差数列{b n}的第8项和第32项，求数列{b n}的通项公式及前n项和S n．18．（12分）在△ABC中，内角A，B，C的对边分别为a，b，c，且A，B，C成等差数列．（1）若b=2，c=2，求△ABC的面积；（2）若sin A，sin B，sin C成等比数列，试判断△ABC的形状．19．（12分）正三棱柱ABC﹣A1B1C1中，D是BC上一点，若AD⊥BC．（1）若底面边长为a，侧棱长为b，求该正三棱柱的表面积、体积．（2）求证：A1B∥平面ADC1．20．（12分）已知数列{a n}的前n项和为S n，且满足S n﹣n=2（a n﹣2），n∈N*（1）证明：数列{a n﹣1}为等比数列；（2）若b n=a n•log2（a n﹣1），数列{b n}的前n项和为T n，求T n．21．（12分）设△ABC的内角A，B，C所对的边分别为a，b，c．且acosC+c=b．（1）求A的大小；（2）若a=1，求△ABC的周长l的取值范围．22．（12分）已知非零的数列{a n}满足：a1=，a n+1=a+a n，（n∈N*）（1）求证：=；（2）若T n=，对于任意的正整数n，3T n﹣log2m﹣5＞0恒成立，求m的取值范围．2017-2018学年黑龙江省大庆实验中学高一（下）期中数学试卷（理科）参考答案与试题解析一．选择题（本大题共12小题，每题5分，共60分）1．（5分）已知数列{a n}是等差数列，a3=4，a7=12，则a11的值为（）A．14B．16C．18D．20【解答】解：根据题意，设等差数列{a n}的公差为d，若a3=4，a7=12，则d==2，则a11=a3+8d=20；故选：D．2．（5分）若a＜b＜0，则下列不等式不能成立的是（）A．|a|＞|b|B．a2＞ab C．D．【解答】解：∵a＜b＜0，∴|a|＞|b|，a2＞ab，，＜（由0＞a﹣b ＞a即可得出）．则下列不等式不能成立的是D．故选：D．3．（5分）下列命题中正确的是（）A．利用斜二测画法得到的正方形的直观图是正方形B．利用斜二测画法得到的平行四边形的直观图是平行四边形C．有两个面平行，其余各面都是平行四边行的几何体叫棱柱D．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台【解答】解：利用斜二测画法得到的正方形的直观图是平行四边形，故A错；利用斜二测画法得到的平行四边形的直观图是平行四边形，正确，由斜二测画法可得B对；有两个面平行，其余各面都是平行四边行，并且每相邻两个四边侧面的公共边都互相平行，这样的几何体叫棱柱，故C错；用一个平行于底面的平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台，故D错．故选：B．4．（5分）在△ABC中，已知三边a=3，b=5，c=7，则三角形ABC是（）A．锐角三角形B．直角三角形C．钝角三角形D．无法确定【解答】解：△ABC中，∵已知三边a=3，b=5，c=7，∴c边为最大边，由于cosC===﹣，∴C=120°，故三角形ABC是钝角三角形，故选：C．5．（5分）已知三棱锥A﹣BCD的各棱长都相等，E为BC中点，则异面直线AB 与DE所成角的余弦值为（）A．B．C．D．【解答】解：取AC中点O，连结DO，EO，∵三棱锥A﹣BCD的各棱长都相等，E为BC中点，∴EO∥AB，∴∠DEO是异面直线AB与DE所成角（或所成角的补角），设三棱锥A﹣BCD的各棱长为2，则DE=DO==，OE=1，∴cos∠DEO===．∴异面直线AB与DE所成角的余弦值为．故选：B．6．（5分）在正方体ABCD﹣A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，给出下列四个推断：①FG∥平面AA1D1D；②EF∥平面BC1D1；③FG∥平面BC1D1；④平面EFG∥平面BC1D1其中推断正确的序号是（）A．①③B．①④C．②③D．②④【解答】解：∵在正方体ABCD﹣A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，∴FG∥BC1，∵BC1∥AD1，∴FG∥AD1，∵FG⊄平面AA1D1D，AD1⊂平面AA1D1D，∴FG∥平面AA1D1D，故①正确；∵EF∥A1C1，A1C1与平面BC1D1相交，∴EF与平面BC1D1相交，故②错误；∵E，F，G分别是A1B1，B1C1，BB1的中点，∴FG∥BC1，∵FG⊄平面BC1D1，BC1⊂平面BC1D1，∴FG∥平面BC1D1，故③正确；∵EF与平面BC1D1相交，∴平面EFG与平面BC1D1相交，故④错误．故选：A．7．（5分）下列命题不正确的是（）A．若任意四点不共面，则其中任意三点必不共线B．若直线l上有一点在平面β外，则l在平面β外C．若一个平面内的任一条直线都平行于另一个平面，则这两个平面平行D．若直线a，b，c中，a与b共面且b与c共面，则a与c共面【解答】解：A．若任意三点必共线，则必有四点共面，∴矛盾，∴A正确．B．根据直线在平面外的定义可知，当直线和平面相交或直线和平面平行时，满足条件，∴B正确．C．若一个平面内的任一条直线都平行于另一个平面，则所有直线都和平面，没有公共点，∴这两个平面平行，∴C正确．D．若三条直线满足两两异面，则结论不成立，∴D不正确．故选：D．8．（5分）四棱锥的三视图如图所示，则最长的一条侧棱的长度是（）A．B．5C．D．2【解答】解：由题意可知几何体是底面为直角梯形，直角边长为：4，2，高为3的梯形，棱锥的高为2，高所在的棱垂直直角梯形的上直角顶点，所以侧棱最长为，底面梯形下底边锐角顶点与棱锥顶点连线，所以长度为：=．故选：A．9．（5分）给出以下四个命题：①若＜＜0，则+＞2；②若a＞b，则am2＞bm2；③在△ABC中，若sinA=sinB，则A=B；④任意x∈R，都有ax2﹣ax+1≥0，则0＜a≤4．其中是真命题的有（）A．①②B．②③C．①③D．③④【解答】解：①若＜＜0，则b＜a＜0，则＞0，则+≥，当且仅当=，即a=b取等号，∵a≠b，∴等号取不到，则+＞2，故①正确，②若a＞b，则当m=0时，不等式am2＞bm2不成立，故②错误，③在△ABC中，若sinA=sinB，由正弦定理得a=b，则A=B；故③正确，④任意x∈R，都有ax2﹣ax+1≥0，则当a=0时，不等式等价为1≥0，即a=0也成立，故④错误，故选：C．10．（5分）已知数列{a n}的首项a1=35，且满足a n﹣a n﹣1=2n﹣1，则的最小值为（）A．2B．C．D．12【解答】解：数列{a n}的首项a1=35，且满足a n﹣a n﹣1=2n﹣1，可得a n=a1+（a2﹣a1）+（a3﹣a2）+…+（a n﹣a n﹣1）=34+（1+3+5+…+2n﹣1）=34+n（1+2n﹣1）=34+n2，则=n+≥2，此时n=，解得n不为自然数，由于n为自然数，可得n=5时，5+=；n=6时，6+=＜，则的最小值为，故选：C．11．（5分）如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，点E，F分别是棱BC，CC1的中点，P是侧面BCC1B1内一点，若A1P∥平面AEF，则线段A1P长度的取值范围是（）A．[1，]B．[，]C．[，]D．[，]【解答】解：如下图所示：分别取棱BB1、B1C1的中点M、N，连接MN，连接BC1，∵M、N、E、F为所在棱的中点，∴MN∥BC1，EF∥BC1，∴MN∥EF，又MN⊄平面AEF，EF⊂平面AEF，∴MN∥平面AEF；∵AA1∥NE，AA1=NE，∴四边形AENA1为平行四边形，∴A1N∥AE，又A1N⊄平面AEF，AE⊂平面AEF，∴A1N∥平面AEF，又A1N∩MN=N，∴平面A1MN∥平面AEF，∵P是侧面BCC1B1内一点，且A1P∥平面AEF，则P必在线段MN上，在Rt△A1B1M中，=，同理，在Rt△A1B1N中，求得A1N=，∴△A1MN为等腰三角形，当P在MN中点O时A1P⊥MN，此时A1P最短，P位于M、N处时A1P最长，==，A1M=A1N=，所以线段A1P长度的取值范围是[，]．故选：B．12．（5分）在△ABC中，若a2﹣c2=2b，，则b等于（）A．3B．4C．6D．7【解答】解：△ABC中，，∴=2，即sinAcosC=2cosAsinC，∴sin（A+C）=3cosAsinC，∴sinB=3cosAsinC，∴=3cosA=3×，化简可得2b2=3（b2+c2﹣a2）；∴再根据a2﹣c2=2b，可得：b2﹣6b=0，解得：b=6．故选：C．二．填空题（本大题共4小题，每小题5分，共20分）13．（5分）已知圆锥底面的半径为1，侧面展开图是一个圆心角为的扇形，则该圆锥的侧面积是3π．【解答】解：∵圆锥底面的半径r=1，侧面展开图是一个圆心角为的扇形，故圆锥的母线l满足：，解得：l=3，∴该圆锥的侧面积S=πrl=3π．故答案为：3π14．（5分）如图所示，为测一建筑物CD的高度，在地面上选取A，B两点，从A，B两点分别测得建筑物顶端的仰角为30°，45°，且A，B两点间的距离为20m，则该建筑物的高度为10（）m．【解答】解：如图所示，设DC=h，Rt△BCD中，∠CBD=45°，∴BC=CD=h；Rt△ACD中，∠CAD=30°，∴==，解得h=10（+1）；∴建筑物CD的高度为10（+1）m．故答案为：10（+1）．15．（5分）设a，b为正实数，且a+b=3，则的最小值为．【解答】解：a，b为正实数，且a+b=3，由柯西不等式可得[（a+2）+（b+1）]（）≥[•+•）2=（a+b）2=9，即有≥，当且仅当=，即a=2b=2，上式取得等号，则的最小值为，故答案为：．16．（5分）已知数列{a n}为公差不为零的等差数列，且{a n}中的项组成的数列a，a，…，a，…恰为等比数列，其中b 1=1，b2=3，b3=17，则b1+b2+…+b n=．【解答】解：设{a n}的首项为a1，a，a，…，a，…恰为等比数列，其中b1=1，b2=3，b3=17，∴（a1+2d）2=a1（a1+16d），得3a1=d，公比q==7，∵a=a 1+（b n﹣1）d，又a=a1•7n﹣1，∴b n=（7n﹣1+2），∴b1+b2+…+b n=（1+7+…+7n﹣1）+n=×+n=，故答案为：．三、解答题（本大题共6小题，共70分）17．（10分）等比数列{a n}中，已知a3=8，a6=64．（1）求数列{a n}的通项公式；（2）若a4，a6分别为等差数列{b n}的第8项和第32项，求数列{b n}的通项公式及前n项和S n．【解答】解：（1）设等比数列{a n}的公比为q，由已知得8=q3，解得q=2，所以a n=2n．（2）由（1）得a4=16，a6=64，则b8=16，b32=64，设数列{b n}的公差为d，则有，解得，∴b n=b2+（n﹣1）d=2n，数列{b n}的通项公式及前n项和S n=na1+=n2+n．18．（12分）在△ABC中，内角A，B，C的对边分别为a，b，c，且A，B，C成等差数列．（1）若b=2，c=2，求△ABC的面积；（2）若sin A，sin B，sin C成等比数列，试判断△ABC的形状．【解答】解：∵A、B、C成等差数列，可得2B=A+C．∴结合A+B+C=π，可得B=．（1）∵，c=2，∴由正弦定理，得sinC===．∵b＞c，可得B＞C，∴C为锐角，得C=，从而A=π﹣B﹣C=．因此，△ABC的面积为S==×=．（2）∵sinA、sinB、sinC成等比数列，即sin2B=sinAsinC．∴由正弦定理，得b2=ac又∵根据余弦定理，得b2=a2+c2﹣2accosB=a2+c2﹣ac，∴a2+c2﹣ac=ac，整理得（a﹣c）2=0，可得a=c∵B=，∴A=C=，可得△ABC为等边三角形．19．（12分）正三棱柱ABC﹣A1B1C1中，D是BC上一点，若AD⊥BC．（1）若底面边长为a，侧棱长为b，求该正三棱柱的表面积、体积．（2）求证：A1B∥平面ADC1．（1）在正三棱柱ABC﹣A1B1C1中，△ABC为等边三角形，，【解答】解：正三棱柱面积=，体积．（2）证明：连接A1C，交AC1于O点，连接OD，∵在△A1CB中，O，D分别为A1C，BC中点，∴OD∥A1B，∴OD⊂平面ADC1，A1B⊄平面ADC1，∴A1B∥平面ADC1．20．（12分）已知数列{a n}的前n项和为S n，且满足S n﹣n=2（a n﹣2），n∈N*（1）证明：数列{a n﹣1}为等比数列；（2）若b n=a n•log2（a n﹣1），数列{b n}的前n项和为T n，求T n．【解答】（1）证明：∵S n﹣n=2（a n﹣2），n∈N*，n≥2时，S n﹣1﹣（n﹣1）=2（a n﹣1﹣2），，两式相减：a n﹣1=2a n﹣2a n﹣1∴a n﹣1=2（a n﹣1），﹣1又n=1时，a1﹣1=2（a1﹣2），得：a1=3，a1﹣1=2．所以数列{a n﹣1}是以2为首项，2为公比的等比数列，（2）由（1）：a n﹣1=2×2n﹣1=2n，∴a n=1+2n．又b n=a n•log2（a n﹣1）=n+n•2n，设数列{n•2n}的前n项和为A n，则A n=2+2×22+3×23+…+n•2n，∴2A n=22+2×23+…+（n﹣1）•2n+n•2n+1，相减可得：﹣A n=2+22+…+2n﹣n•2n+1=﹣n•2n+1，化为：A n=（n﹣1）•2n+1+2．数列{b n}的前n项和为T n=（1+2+…+n）+A n=+（n﹣1）•2n+1+2．21．（12分）设△ABC的内角A，B，C所对的边分别为a，b，c．且acosC+c=b．（1）求A的大小；（2）若a=1，求△ABC的周长l的取值范围．【解答】解：（1）∵acosC+c=b．∴sinAcosC+sinC=sinB，可得：sinAcosC+sinC=sin（A+C）=sinAcosC+cosAsinC，∴sinC=cosAsinC，∵C∈（0，π），sinC≠0，可得：cosA=，∵A∈（0，π），∴A=．（2）由正弦定理可得b===sinB，c==sinC，则l=a+b+c=1+（sinB+sinC），由A=，B+C=，则sinB+sinC=sinB+sin（﹣B）=sinB+cosB=sin（B+），即有l=1+2sin（B+），由于0＜B＜，则＜B+＜，＜sin（B+）≤1，即有2＜l≤3．则有△ABC的周长l的取值范围为（2，3]．22．（12分）已知非零的数列{a n}满足：a1=，a n+1=a+a n，（n∈N*）（1）求证：=；（2）若T n=，对于任意的正整数n，3T n﹣log2m﹣5＞0恒成立，求m的取值范围．【解答】解：（1）证明：由已知a1=，a n+1=a+a n，（n∈N*），可得===﹣，所以=；（2）由（1）知T n==﹣+﹣+…+﹣=﹣=2﹣，=a+a n＞a n，得数列{a n}是单调递增，由已知a n+1所以{T n}是单调递增，所以T n的最小值为T1=2﹣=2﹣=，对于任意的正整数n，3T n﹣log2m﹣5＞0恒成立，可得5+log2m＜3×，解得0＜m＜，所以m的取值范围是（0，）．。

大庆实验中学2017-2018学年度下学期期中考试高一数学理科试题一、选择题(本大题共12小题，每题5分，共60分)1.已知数列是等差数列，，则的值为（）A. 14B. 16C. 18D. 20【答案】D【解析】分析：根据条件列关于首项与公差的方程组，解得公差与首项，再根据通项公式求的值.详解：因为，所以因此，选D.点睛：本题主要考查等差数列基本量，主要考查学生基本运算能力.2.若，则下列不等式不能成立的是（）A. B. C. D.【答案】D【解析】，有，A正确；因为，所以，B正确；，C正确；当时，，，不成立，D错误。

故选D.3.下列命题中正确的是( )A. 利用斜二测画法得到的正方形的直观图是正方形B. 利用斜二测画法得到的平行四边形的直观图是平行四边形C. 有两个面平行，其余各面都是平行四边形的几何体叫棱柱D. 用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台【答案】B【解析】分析：根据斜二测画法垂直条件转化为45度关系，垂直方向的长度也减半，由此判断A,B真假；根据棱柱以及棱台定义确定C,D真假.详解：利用斜二测画法得到的正方形的直观图是平行四边形；利用斜二测画法得到的平行四边形的直观图是平行四边形；有两个面平行，其余各面都是平行四边形的几何体不一定是棱柱；用一个平行于底面的平面去截棱锥，底面与截面之间的部分组成的几何体才是棱台；因此B正确，选B.点睛：本题主要考查斜二测画法以及棱柱、棱台定义，考查学生识别与理解能力.4.在中，已知三边，，，则是（　）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定【答案】C【解析】分析：研究三角形形状可从最大角入手，利用余弦定理，根据余弦值的正负确定三角形形状.详解：因为C角最大，且，所以C角为钝角，是钝角三角形，选C.点睛：利用余弦定理可判断三角形形状：最大角余弦值小于零，则三角形为钝角三角形；最大角余弦值等于零，则三角形为直角三角形；最大角余弦值大于零，则三角形为锐角三角形.5.已知三棱锥的各棱长都相等，为中点，则异面直线与所成角的余弦值为( )A. B. C. D.【答案】B【解析】分析：求线面角关键找平行，利用三角形中位线是解决本题的关键，再根据余弦定理求求得结果.详解：取AC中点M，则因为为中点，因此ME平行AB，从而异面直线与所成角等于∠MED，因为三棱锥的各棱长都相等，设为1，则，即异面直线与所成角的余弦值为，选B.点睛：本题主要考查求异面直线所成角，线线角找平行，主要考查学生空间想象能力以及转化能力.6.在正方体中，分别是、、的中点，给出下列四个推断：①平面；②平面；③平面；④平面平面其中推断正确的序号是（）A. ①③B. ①④C. ②③D. ②④【答案】A【解析】FG平面；与相交，所以②错；④错FG平面；选A.7.下列命题不正确的是（）A. 若任意四点不共面，则其中任意三点必不共线B. 若直线上有一点在平面外，则在平面外C. 若一个平面内的任一条直线都平行于另一个平面，则这两个平面平行D. 若直线中，与共面且与共面，则与共面【答案】D【解析】A．若任意三点必共线，则必有四点共面，∴矛盾，∴A正确．B．根据直线在平面外的定义可知，当直线和平面相交或直线和平面平行时，满足条件，∴B正确．C．若一个平面内的任一条直线都平行于另一个平面，则所有直线都和平面，没有公共点，∴这两个平面平行，∴C正确．D．若三条直线满足两两异面，则结论不成立，∴D不正确．故选：D．8. 某四棱锥的三视图如图所示，则最长的一条侧棱长度是（）A. B. 5 C. D.【答案】A【解析】试题分析：由三视图可知该四棱锥底面为直角梯形，底面，如下图所示由上图可知：，，所以，．考点：三视图．9.给出以下四个命题：①若，则；②若，则；③在中，若，则；④任意，都有，则.其中是真命题个数为（）A. 1个B. 2个C. 3个D. 4个【答案】B【解析】分析：判断命题真假时，举出反例即可否定，若肯定需论证.反例一般在特殊位置上进行举证，如零，等号等，而论证需用演绎推理，如利用正弦定理，基本不等式等.详解：若，则=2;若，则；在中，若，则；任意，都有，则.综上真命题只有①③，选B.点睛：要判定一个全称命题是假命题，只要举出集合中的一个特殊值，使不成立即可.要判断存在性命题是真命题，只要在限定集合内至少能找到一个，使成立即可，否则就是假命题.10.已知数列的首项，且满足，则的最小值为( )A. B. C. D.【答案】C【解析】分析：先根据叠加法求数列通项公式，再利用对勾函数单调性确定函数最值.详解：因为，所以；因此，因为，所以当时，取最小值，选C.点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.11.如图，在棱长为1的正方体中，点分别是棱，的中点，是侧面内一点，若平面，则线段长度的取值范围是（）A. B. C. D.【答案】B【解析】分析：先判断出点的位置，确定使得取得最大值和最小值时点的位置，然后再通过计算可求得线段长度的取值范围．详解：如下图所示，分别取棱的中点M、N，连MN，，∵分别为所在棱的中点，则，∴MN∥EF，又MN⊄平面AEF，EF⊂平面AEF，∵，∴四边形为平行四边形，∴，又平面AEF，AE⊂平面AEF，∴∥平面AEF，又，∴平面∥平面AEF．∵P是侧面内一点，且∥平面AEF，∴点P必在线段MN上．在中，．同理，在中，可得，∴为等腰三角形．当点P为MN中点O时，，此时最短；点P位于M、N处时，最长．∵，．∴线段长度的取值范围是．故选B．点睛：本题难度较大，解题时要借助几何图形判断得出使得取得最值时的点P的位置，然后再根据勾股定理进行计算．12.在中，若，,则等于( )A. 3B. 4C. 6D. 7【答案】C【解析】分析：先根据正弦定理以及余弦定理将条件化为边的关系：，再与已知条件联立方程组，可得结果.详解：因为，所以，因此选C.点睛：解三角形问题，多为边和角的求值问题，这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系，从而达到解决问题的目的.其基本步骤是：第一步：定条件，即确定三角形中的已知和所求，在图形中标出来，然后确定转化的方向.第二步：定工具，即根据条件和所求合理选择转化的工具，实施边角之间的互化.第三步：求结果.二、填空题 (本大题共4小题，每小题5分，共20分)13.已知圆锥底面圆的半径为1,侧面展开图是一个圆心角为的扇形,则该圆锥的侧面积是____________.【答案】【解析】分析：先根据扇形弧长公式解得母线长，再根据圆柱侧面积公式求面积.详解：因为侧面展开图是一个圆心角为的扇形,所以，因此该圆锥的侧面积是.点睛：明确圆锥轴截面与侧面展开图之间关系是解决这类问题的关键，其中相应的公式需熟记.14.如图所示，为测一建筑物的高度，在地面上选取两点，从两点分别测得建筑物顶端的仰角为，且两点间的距离为，则该建筑物的高度为________.【答案】【解析】分析：根据直角三角形表示直角边，再根据直角边之间关系联立方程，解得高.详解：设高度为h，则，点睛：研究两个直角三角形边角关系时，需从公共边出发，结合已知条件列出等量关系，进而求得未知量.15.设为正实数，且，则的最小值为________.【答案】【解析】∵,令，∴，∴，∴又∵∴；当且仅当时，即时取得最小值，∴的最小值为.16.已知数列为公差不为零的等差数列，且中的项组成的数列恰为等比数列，其中，则________.【答案】【解析】分析：先根据等比中项性质得到等差数列公差与首项关系，再求等比数列公比，进而得等比数列通项公式，解出，最后根据分组求和法得结果.详解：设数列公差为，则，因此从而点睛：本题采用分组转化法求和，将原数列转化为一个等差数列与一个等比数列的和. 分组转化法求和的常见类型主要有分段型（如），符号型（如），周期型　（如）三、解答题（本大题共6小题，共70分）17.等比数列中，已知.（1）求数列的通项公式；（2）若分别为等差数列的第项和第项，求数列的通项公式及前项和.【答案】（1）；（2）.【解析】分析：(1)先根据等比数列通项公式列出公比与首项的方程组，解得公比与首项，代入通项公式即得结果，（2）先根据等差数列通项公式列出公差与首项的方程组，解得公差与首项，代入通项公式即得数列的通项公式，代入求和公式即得.详解：(1)设的公比为，由已知得，解得，所以.(2)由(1)得，则，设的公差为，则有，解得，，且数列前项和.点睛：在解决等差、等比数列的运算问题时，有两个处理思路,一是利用基本量,将多元问题简化为首项与公差（公比）问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现，是解决等差、等比数列问题既快捷又方便的工具，应有意识地去应用.18.在中，角的对边分别为，且成等差数列（1）若，求的面积（2）若成等比数列，试判断的形状【答案】【解析】试题分析：（1）在解决三角形的问题中，面积公式最常用，因为公式中既有边又有角，容易和正弦定理、余弦定理联系起来；在求面积时注意角优先；（2）在判断三角形的形状时，一般将将已知条件中的边角关系利用正弦定理或余弦定理转化为角角关系或边边关系，再利用三角变换或代数式恒等变形（因式分解，配方等）求解，注意等式两边的公因式不要约掉，要移项提公因式，否者会漏解试题解析：（1）由A，B，C成等差数列，有2B=A+C（1）因为A，B，C为△ABC的内角，所以A+B+C=π．（2）得B=b2=a2+c2-2accosB所以（解得或（舍去）所以（2）由a，b，c成等比数列，有b2=ac（4）由余弦定理及（3），可得b2=a2+c2-2accosB=a2+c2-ac再由（4），得a2+c2-ac=ac，即（a-c）2=0因此a=c从而A=C（5）由（2）（3）（5），得A=B=C=所以△ABC为等边三角形．考点：等差数列和等比数列的性质，三角形形状的判断，余弦定理的应用．19.正三棱柱中，是上一点，若．（）若底面边长为，侧棱长为，求该正三棱柱的表面积、体积．（）求证：平面．【答案】（），（）见解析【解析】试题分析：（1）由等边三角形、矩形的面积公式可得柱体的表面积；由体积公式可得柱体的体积。