山东省济南市二十七中八年级数学《2.2平方根》学案 人教新课标版

2.2.2平方根（2）【教学目标】：1.了解平方根的概念、开平方的概念.2.明确算术平方根与平方根的区别与联系.3.进一步明确平方与开方是互为逆运算.【教学重难点】：平方根与算术平方根的区别与联系.平方根：如果一个数x 的平方等于a ，即a x =2，那么这个数x 就叫做a 的平方根（也叫二次方根）。

注意：（1）一个正数a 必须有两个平方根，一个是a 的算术平方根“a ” ，另外一个是“-a ”,读作“负根号a ” ，它们互为相反数；（2）0只有一个平方根，是它本身；（3）负数没有平方根。

3、开平方：求一个数a 的平方根的运算。

其中a 叫做被开方数。

⎩⎨⎧<-≥==)0()0(2a a a a a a ()a a =2()0≥a探讨，总结：平方根与算术平方根的联系与区别联系：(1)具有包含关系：平方根包含算术平方根，算术平方根是平方根的一种.(2)存在条件相同：平方根和算术平方根都是只有非负数才有.(3)0的平方根，算术平方根都是0.区别：(1)定义不同：“如果一个数的平方等于a ，这个数就叫做a 的平方根”；“非负数a 的非负平方根叫a 的算术平方根”.(2)个数不同：一个正数有两个平方根，而一个正数的算术平方根只有一个.(3)表示法不同：正数a 的平方根表示为±a ，正数a 的算术平方根表示为a .(4)取值范围不同：正数的平方根一正一负，互为相反数；正数的算术平方根只有一个.一个正数有两个平方根，它们互为相反数。

0只有一个平方根，它是0本身。

负数没有平方根。

一个正数a 有两个平方根,它们互为相反数。

正数a 的正的平方根,记作“a ”，正数a 的负的平方根,记作“-a ”，这两个平方根合在一起记作“±a ”。

开平方与平方互为逆运算。

因此，我们可以通过平方运算来求一个数的平方根。

三、巩固练习：1、判断题（正确的打“∨”，错误的打“×”）；（1）任意一个数都有两个平方根，它们互为相反数； （ ）（2）数a（ ）（3）—4的算术平方根是2； （ ）（4）负数不能开平方； （ ）（5=8． （ ）（6）－52的平方根为－5 （ ）（7）正数的平方根有两个，它们是互为相反数 （ ）（8）0和负数没有平方根 （ ）（9）4是2的算术平方根 （ ） （10）9的平方根是±3 （ ）（11）因为161的平方根是±41,所以161=±41 （ ） 2.判断下列各数是否有平方根？并说明理由.(1)(－3)2；(2)0；(3)－0.01；(4)－52；(5)－a 2；(6)a 2－2a +23.求下列各数的平方根.(1)121；(2)0.01；(3)297；(4)(－13)2；(5)－(－4)34.对于任意数a ，2a 一定等于a 吗？5.a 中的被开方数a 在什么情况下有意义，(a )2等于什么？6、121---x x 有意义，则x 的范围___________7、如果a (a ＞0)的平方根是±m ，那么（ ）A.a 2=±mB.a =±m 2C.a =±mD.±a =±m_a的负平方根 _a的正平方根 _ 被开方数_ 根号四、作业既 的平方根是 。

数学初二上2.2平方根（二）学案本卷须知1.答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2、选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3、请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4、保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

主备：宋冰副备：张云霞审核：备课时间：第一周上课时间：第二周第一版块：前奏版第一环节：复习提问是2的算术平方根1、以下说法中不正确的选项是〔〕A.2B.2的平方根是2C.2的算术平方根是22、0的算术平方根是0.25的算术平方根是第二版块：启动版第二环节：引入新课平方等于4的数有几个，它们是多少？3的平方等于9，平方等于9的数还有吗？是多少？第三环节：展示目标1.了解平方根、开平方的概念.2.明确算术平方根与平方根的区别和联系.3.进一步明确平方与开平方是互逆的运算关系.第三版块：核心板第四环节：自主学习合作探究教材40－－－41页一般地，如果一个数的平方等于A，那么这个数叫做A的平方根或二次方根.而把正的平方根叫算术平方根。

表达式为：假设X2＝A，那么X叫做A的平方根.记作：正数A有两个平方根，它们互为相反数例如：〔±4〕2＝16，那么＋4和－4都是16的平方根；即16的平方根是±4；4是16的算术平方根.第五环节：展示汇报小组比赛展示探究结果例3求以下各数的平方根：〔1〕64；〔2〕；〔3〕0.0004；〔4〕；〔5〕11教材想一想第四版块：强化版第六环节：课堂小结平方根与算术平方根关系2、正数的平方根的互为相反数3、第七环节：反馈检测【一】选择题1、以下说法中不正确的选项是〔〕 A.2-是2的平方根B.2是2的平方根C.2的平方根是2D.2的算术平方根是22、41的平方根是〔〕A.161B.81C.21D.21±3、以下各式中，正确的个数是〔〕 ①3.09.0=②34971±=③23-的平方根是－3 ④()25-的算术平方根是－5⑤67±是36131的平方根A.1个B.2个C.3个D.4个【二】填空题4.如果某数的一个平方根是－6，那么这个数为＿＿＿＿＿＿＿＿、5.如果正数m 的平方根为1x +和3x -，那么m 的值是、6、16的平方根是.【三】解答题求以下各式的值。

导学案八年级上册第二章 实数 第2节 平方根（2）学习目标：1、了解平方根的定义，会用符号表示一个非负数的平方根；2、会求一个非负数的平方根。

3、正确理解平方根的性质。

预习案课前导学：1、阅读课本P27-28：想一想（1）9的算术平方根是3，也就是说，3的平方是9，还有其他的数，它的平方也是9吗？（2）平方等于254的数有几个？平方等于0.64的数呢？2、总结一般地，如果一个数的平方等于a ，那么这个数叫做a 的平方根或二次方根，也就是说，如果x 2=a ，那么， 叫做 的平方根.尝试练习1、练习：（1）因为22=_____，（-2）2=______，所以2和-2都是_____的平方根．（2）3有______个平方根，它们互为______数，记作_______．2、探究：请同学们思考以下问题（1）一个正数有几个平方根？（2）0有几个平方根?（3）负数呢？结论：一个正数有＿＿个平方根，且它们互为＿＿ ，用 表示其中正的平方根，读作“ ”，另一个负的平方根记为 ，合起来可记作 ；求一个数的平方根的运算叫做 ，其中a 叫做 ；只有一个平方根，它是＿＿ ； 没有平方根。

学习案知识点拨1、 平方根的符号表示；2、 平方根与算术平方根的关系；3、 被开方数的非负性；课内训练1、0.36的平方根是 ；算术平方根是 ； 16的算术平方根是 ； 81的平方根是 。

=＿＿＿＿； =＿＿＿＿。

2、例3 求下列各数的平方根：（1）64； （2）12149； （3）0.0004； （4）（－25）2； （5）11。

3、想一想（1）（64）2等于多少？（12149）2等于多少？（2）（2.7）2等于多少？（3）对于正数a ，（a ）2等于多少？反馈案基础训练1、填空：25的平方根是_________；2)5(- =_________；(5)2=_________. 2、求下列各数的平方根：900 ， 6449，14 ， 0拓展提高求下列各式中的x 的值1．1962=x 2．01052=-x。

平方根一、学习目标：1．明白得并把握算术平方根的概念．2．会用根号表示一个非负数的算术平方根．3．会求一个非负数的算术平方根．二、问题与题例：1．问题一：x 2=2，y 2=3，z 2=4，w 2=5，已知幂和指数，求底数，你能求出来吗？2．问题二：例1 求以下各数的算术平方根：（1）900； （2）1； （3）6449； （4）14． 3．问题三：内容1：例2 自由下落物体的高度h （米）与下落时刻t （秒）的关系为h =4．9t 2．有一铁球从19．6米高的建筑物上自由下落，抵达地面需要多长时间？三、目标检测题：1．填空题：（1）假设一个数的算术平方根是7，那么那个数是 ；（2）9的算术平方根是 ；（3）232⎪⎭⎫ ⎝⎛的算术平方根是 ； （4）若22=+m ，那么(m +2)2= ．2．求以下各数的算术平方根：36，144121，15，0．64，10－4，225，0)65(． 3．如图，从帐篷支撑竿AB 的顶部A 向地面拉一根绳索A C固定帐篷．假设绳索的长度为5．5米，地面固定点C 到帐篷支撑竿底部B 的距离是4．5米，那么帐篷支撑竿的高是多少米？四、配餐作业题：A 组 巩固基础1．1．假设一个数的算术平方根是5，那么那个数是 ；C B A2．16的算术平方根是 ；3．()23-的算术平方根是 ；4．假设31=-x ，那么x = ． B 组 强化训练1．在实数五、73、3、4中，无理数是（ ）．A ．5B ．73C ．3D ．4C 组延伸拓广 1．已知()0232212=++++-z y x ，求x+y+z 的值．2．若x ，y 知足52112=+-+-y x x ，求xy 的值．3．求55=-+x x 中的x ．4．假设115+的小数部份为a ，115-的小数部份为b ，求a +b 的值．5．△ABC 的三边长别离为a ，b ，c ，且a ，b 知足04412=+-+-b b a ，求c 的取值范围． CA。

课题：2.2.2平方根教学目标：1.了解平方根、开平方的概念，明确算术平方根与平方根的区别和联系.2.进一步明确平方与开平方是互逆的运算关系.3.培养学生求同与求异的思维，通过比较提高思考问题、辨析问题的能力.教学重点与难点：重点：了解平方根与算术平方根的区别与联系，会利用这个互逆运算关系求某些非负数的算术平方根和平方根．难点：平方根与算术平方根的区别和联系；负数没有平方根，即负数不能进行平方根的运算.课前准备：多媒体课件．教学过程：一、创设情境，引入新课（课件展示）1.什么叫做算术平方根？怎样表示?2.填空: 9的算术平方根，17的算术平方根.3.我们已经学习过哪些运算？它们中互为逆运算的是什么？4.什么叫乘方？什么叫幂？5.填空:（1）3 2 = ，(－3)2= ；（2）(0.8)2= ， (－0.8)2= .6.平方等于9的数有几个？平方等于0.64的数有几个？处理方式：提问学生一一作答，不足之处由其他学生补充.第1题:一般地，如果一个正数x的平方等于a,即x2 =a ,那么这个正数x叫做a的算术平方根.读作：“根号a”,a叫做被开方数.0的算术平方根是0.即 =0.负数没有算术平方根.第2题: 9的算术平方根 3 ，17的算术平方根17.第3题：学习过了加、减、乘、除、乘方五种运算.其中加法与减法互为逆运算；乘法与除法互逆.第4题：求相同因数的积的运算叫做乘方；乘方运算的结果叫做幂.第5题： 32= 9 ，(－3)2= 9 ；(0.8)2= 0.64 ，(－0.8)2= 0.64 .第6题:平方等于9的数有两个；平方等于0.64的数有两个.这6道题目小组交流，教师点拨，代表回答，从而引出课题.设计意图：这一环节主要是复习旧知识和提出问题,由上节课的“算术平方根”的求法使学生能明白“平方”和“算术平方根”的关系，感知负数没有算术平方根、算术平方根是一个非负数，很显然，负数不是9的算术平方根，从而导入新课.本环节采用小组互查的方式，可以更好的激发学生的学习兴趣.二、合作探究，交流互动（一）探究新知：填空：（课件展示）32=( )(－3)2=( ) ( )2=9 02=0(12)2=( )()214= ( )2=－4 (12-)2=( )处理方式：让学生先思考后回答：9，9，14，14，0，不存在.(教师进一步引导学生发现：2(3)9±=，211()24±=，02=0，平方得－4的数不存在.)我们就说3和-3都是9的平方根，同理，14的平方根是 ，0的平方根是 .类比算术平方根的概念，你能得出平方根的概念吗?引导学生回答，14的平方根是12和12-，0的平方根是0. （二）形成概念：一般地，如果一个数的平方等于a ，那么这个数叫做a 的平方根或二次方根．而把正的平方根叫做a 的算术平方根．表达式为:若x 2=a ，那么x 叫做a 的平方根． 记作．例如：(±4)2 =16，则+4和－4都是16的平方根；即16的平方根是±4；4是16的算术平方根．处理方式：通过学生观察特例，让学生对照算术平方根概念归纳平方根概念并举例．（三）探索平方与开平方的关系:（课件展示）x 2=a 这种运算叫 ， x =这种运算叫 . 乘方运算与开方运算的关系是什么? 给出几组具体的数据，由平方探知开平方与平方的互逆关系．处理方式：提问学生，然后有人说前者叫乘方运算，后者叫开方运算. 再小组合作得出结论，互为逆运算.即若x 2=a ，则x =x =a = x 2. 设计意图：形成“平方根”的概念.在列举一些具体数据的感性认识基础上,由平方运算反推出平方根的概念和定义，并让学生非常熟练地进行平方和平方根之间的互化，明白它们之间的互逆关系.（四）平方根的性质:议一议：（课件展示）(1)一个正数有几个平方根? (2)0有几个平方根? (3)负数呢？处理方式：让学生照着前面引例回答，例如2(3)9±=，则一个正数9有两个平方根3和－3,它们互为相反数.因为只有零的平方为零, 所以0有一个平方根是零.因为任何数的平方都不是负数, 所以负数没有平方根, 例如－4没有平方根.然后教师总结，一个正数有两个平方根，且它们互为相反数；0有一个平方根是0，负数没有平方根.设计意图：要求学生能熟练地求出一个数的平方根，然后由题中的数据探索出正数、0、负数的平方根的个数.（五）概念辨析：平方根与算术平方根的联系与区别？处理方式：学生讨论交流，在导学案上完成后再展示说明，学生之间互相补充．教师适时点评.平方根与算术平方根的联系与区别：联系：(1)具有包含关系：平方根包含算术平方根，算术平方根是平方根的一种.(2)存在条件相同：平方根和算术平方根都是只有非负数才有.(3)0的平方根，算术平方根都是0.区别：(1)定义不同：“如果一个数的平方等于a ，这个数就叫做a 的平方根”；“非负数a 的非负平方根叫a 的算术平方根”.(2)个数不同：一个正数有两个平方根，而一个正数的算术平方根只有一个.(3)表示法不同：正数a 的平方根表示为±a ，正数a 的算术平方根表示为a .(4)取值范围不同：正数的平方根一正一负，互为相反数；正数的算术平方根只有一个. 设计意图：形成“平方根”的概念．在列举一些具体数据的感性认识的基础上，由平方运算反推出平方根的概念和定义，并让学生对有关平方根一些常见表示作对比，明白它们之间的异同，进一步理解平方根的概念，可以避免一些初学时的常见错误.平方根与算术平方根的区别是本节课的一大难点，也是学生经常容易出错的地方．辨析开平方与平方的对比﹑辨析概念“平方根”与“算术平方根”的区别与联系，使之与上一节课紧密联系,并作以对比,这样有利于学生的理解与掌握,对这一抽象的概念掌握才能比较牢靠．三、例题解析，应用新知（一）例题示范（多媒体出示）例3 求下列各数的平方根:(1)64；(2)49121；(3) 0.0004；(4)()225-；(5) 11.处理方式：先给学生10秒钟时间观察例3第（1）题，让学生口述解题过程，教师板书.在学生口述过程中，教师可进行有针对性的提问，让学生进一步理解并规范如何使用平方根. 其余题目让四名学生主动到黑板板演，其他学生在练习本上完成．教师巡视，适时点拨．学生完成后及时点评，借助多媒体展示学生出现的问题进行矫正．跟踪训练：1. 判断下列各数是否有平方根？并说明理由.(1)(－3)2； (2)0； (3)－0.01； (4)－52； (5)－a2 ； (6) a2－2a+2.2. 25的平方根是_________；)2=_________.3. 求下列各数的平方根：1.44， 0， 8，10049， 441， 196， 10－4。

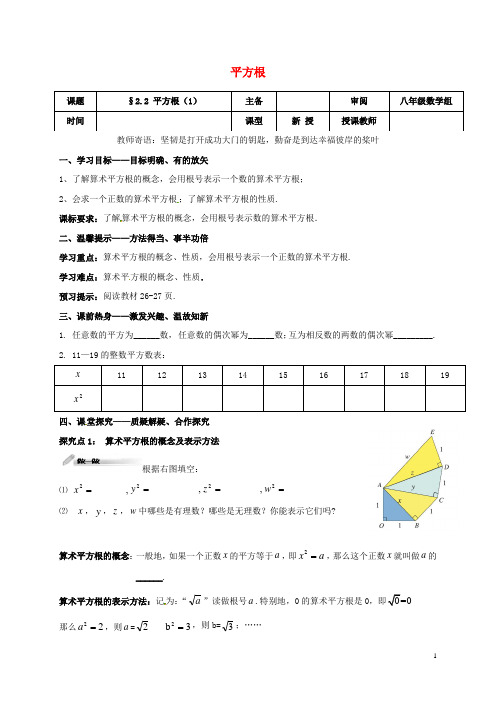
平方根教师寄语：坚韧是打开成功大门的钥匙，勤奋是到达幸福彼岸的桨叶一、学习目标——目标明确、有的放矢1、了解算术平方根的概念，会用根号表示一个数的算术平方根；2、会求一个正数的算术平方根；了解算术平方根的性质.课标要求：了解算术平方根的概念，会用根号表示数的算术平方根． 二、温馨提示——方法得当、事半功倍学习重点：算术平方根的概念、性质，会用根号表示一个正数的算术平方根. 学习难点：算术平方根的概念、性质． 预习提示：阅读教材26-27页. 三、课前热身——激发兴趣、温故知新1. 任意数的平方为______数， 任意数的偶次幂为______数；互为相反数的两数的偶次幂_________.2. 11—19的整数平方数表：x11 12 13 14 15 16 17 18 19 2x四、课堂探究——质疑解疑、合作探究 探究点1： 算术平方根的概念及表示方法根据右图填空：⑴ ______,2=x _________,2=y _______,2=z _______2=w⑵ x ，y ，z ，w 中哪些是有理数？哪些是无理数？你能表示它们吗?算术平方根的概念：一般地，如果一个正数x 的平方等于a ，即a x =2，那么这个正数x 就叫做a 的______.算术平方根的表示方法：记为：“a ”读做根号a .特别地，0的算术平方根是0，即0=0那么22=a ，则a =2 3b 2=，则b=3；……课题 §2.2 平方根（1）主备 审阅 八年级数学组时间课型新 授授课教师一个非负数的算术平方根就可以表示为a探究点2：求算术平方根例题： 写出下列各数的算术平方根，并用符号表示出来：⑴ 900； ⑵ 1； ⑶ 6449； ⑷ 14； ⑸ -410练习：1．求下列各数的算术平方根，并用符号表示出来：⑴ 1600；⑵ 0；⑶ 121625；⑷ 0.25；⑸ 52－32；⑹ 1916；⑺ 17；⑻ │－π│0．2．求下列各式的值．（1）36289； （2）2(13)-； （3）81； （4）226160-．探究点3：算术平方根的非负性 公式：⑴a a ≥0)；⑵a ≥0 例题：已知()2130x y x y z -++++=求x ，y ，z 的值.练习：1. 如果()22+30x x y -+-=，则x y -的值为________．2．已知a 为实数，那么2a -等于( )A ． aB ． a -C ． -1D ． 0 3．若11x x ---2()x y =+，则x y -的值为（ ）A ．－1B ．1C ．2D ．3探究点4：利用算术平方根解决实际问题例题：自由下落物体的高度h （米）与下落时间t(秒)的关系为24.9h t =,有一铁球从19.6 米高的建筑物上自由下落，到达地面需要多长时间 ？练习：1．如图，从帐篷支撑杆AB 的顶部A 向地面拉一根绳子AC 固定帐篷，若绳子的长度为5.5米，地面固定点C 到帐篷支撑杆底部B 的距离是4.5米，则帐篷支撑杆的高是多少？2. 小明房间的面积为10.8米2，房间地面恰由120块相同的正方形地砖铺成，每块地砖的边长是多少？五、巩固提升——（有效训练、反馈矫正）1．a 的算术平方根是它本身，则a 为（ ）A ．0B ．1C ．-1D ．0或1 2．下列说法正确的是（ ）A ．5是25的算术平方根B ．±4是16的算术平方根C ．－6是（－6）2的算术平方根D ．0.01是0.1的算术平方根3．下列各式正确的是（ ）A ．25-=－5B ．25-=5C ．2(3)-=－3D ．2(3)-=3 4．4的算术平方根是（ ）A ．2±B ．2C ．2±D ．25．9的算术平方根是（ ）A ． ±3B ． 3C ． －3D ．6．若2(2)a -=4，那么下列结论正确的是（ ）A ．a =6B ．a =-2C ．a =6或a =-2D ．以上都不对7.81的算术平方根为_________. 8．(－π)2的算术平方根为_____.9．已知012=-++b a ，那么2007)b a (+的值为（ ）A ．－1B ．1C ．20073D ．20073-10．一个自然数的算术平方根是n ，那么大于这个自然数且与它相邻的自然数是（ ） A.n +1B.n 2+1 C.12+n D.n +111n 为（ ）A ．2B ．3C ．4D ．512. 已知322+-+-=x x y ，那么x y 的算术平方根为___________.。

《2.2平方根（2）》导学案【教学目标】1.了解平方根的概念，会进行有关平方根的运算；2.理解算术平方根与平方根的联系与区别。

【教学重点】平方根的概念和性质。

【教学难点】平方根与算术平方根的区别。

【教学方法】自主探究【教学流程】（一）自主梳理：（独学）认真阅读课本P27-29页，回答下列问题：1.（1）9的算术平方根是3，也就是说，3的平方是9，还有其他的数，它的平方也是9吗？（2）平方等于425的数有几个？平方等于0.64的数呢？2.3.平方根的定义：一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根．而把正的平方根叫做a的算术平方根．表达式为:若x2=a，那么x叫做a的平方根．记作a．例如:(±4)2=16，则+4和－4都是16的平方根；即16的平方根是±4；4是16的算术平方根。

(二) 质疑释疑：（对学）4. 求下列各数的平方根：（写出解答过程）（1）1.44 （2）10049（3）0.0004 （4）（-25）²（5）85.求满足下列各式的未知数x．（1）x ²=49 （2）x ²=25816.计算：（1）2 （2）2 （3）2（4 （5归纳：2= （a ≥0）a ==（三）合作交流（群学）7.某数的平方根是a+1和2a-7，则这个数是多少？8.已知2x-1的平方根是±6,2x+y-1的平方根是±5，求2x-3y+4的平方根。

（五）课堂小结教师点拨：平方根和算术平方根的区别：①概念不同②表示方法不同③读法不同④结果和个数不同(六)板书设计：2.2平方根（2）1.平方根的定义2.典型例题3.合作探究（七）作业布置（课外拓展单）分类完成A 、B 两类作业【教后反思】。

§2.2 平方根（1）姓名_________ 学号____ 学习目标：1、知道算术平方根、平方根的概念.2、会用符号表示算术平方根、平方根.3、会求算术平方根、平方根.预习导航一、知识储备：计算并熟记：（1）写出1—25的平方：（2）写出-25—-1的平方：（3）根据（1）、（2），平方等于一个正数的数有几个？二、先认真学习课本38-42页，然后解答下列问题：（一）概念：1、（1）算术平方根如果一个__________平方等于a ，即2x a ，那么________叫做a 的算术平方根. 注：① 正数a 的算术平方根记作________，其中a _____0.② 0的算术平方根为________.③ 只有当a _____0时，数a 才有算术平方根.（2）平方根如果一个__________平方等于a ，即2x a ，那么______叫做a 的平方根(二次方根). 注：① 一个正数a 有_________个平方根，且它们互为________，记为________；② 0有一个平方根，就是_________；③负数没有平方根.（3）比较这两个概念，你发现了什么？一个正数的平方根有______个，而算术平方根只有_____个；一个正数的算术平方根是一个正数，而平方根是____________.（4）开平方求一个数a 的____________运算叫做开平方.其中a 叫做________.注：①开平方运算与平方运算互为__________.②一个正数开平方运算的结果有________个.③负数不能进行开平方运算.即只有a _______0时， a 才有意义. （二）求算术平方根、平方根4、模仿例题，求下列各数的算术平方根（1）361 （2）12164 （3）2.25 （4）17 （5）0 （6）410 例：求900的算术平方根解：230900 90030 山东大学附属中学初二数学学案 北师大版八年级（上）第二章5、模仿例题，求下列各数的平方根（1）124（2）212 （3）14 例：求900的平方根. 解：2(30)900 90030 （三）巩固理解 1、49的平方根是＿＿＿＿；算术平方根是______. 2、36 有 个平方根，它们是 ；它们的和是 ；它们的关系是 . 3、0.04的算术平方根是_________，开平方等于±5的数是_______.4、23的算术平方根是_______，213的算术平方根是___________.5、81的平方根是 ；2(5)的平方根是 ；(－11)2的平方根是______.6、算术平方根等于它本身的数是＿＿＿＿；平方根等于它本身的数是＿＿＿＿.7、下列说法：①任何数都有算术平方根；②一个数的算术平方根一定是正数；③ a 2的算术平方根是a ；④（π-4）2的算术平方根是π-4；⑤算术平方根不可能是负数.其中，不正确的有（ ） A.2个 B.3个 C. 4个 D.5个8、下列说法正确的是（ ）A.－2是－4的平方根B.2是(－2)2的算术平方根C.(－2)2的平方根是2D.8的平方根是49、已知正方形的边长为a ，面积S ，则（ ） A.S=a B.S 的平方根是a C.a 是S 的算术平方根 D.a=±s10、（1）写出下列各数的算术平方根.①121 ②144169③ 46 ④29 ⑤ 0.09 ⑥11（2）写出下列各数的平方根. ①484 ②22549③ 0.0196 ④ 7 ⑤ 28 三、预习小结：。

2.2平方根(二)学案学习目标：(一)教学知识点1.了解平方根的概念、开平方的概念.2.明确算术平方根与平方根的区别与联系.3.进一步明确平方与开方是互为逆运算.(二)能力训练要求1.加强概念形成过程的教学，让学生不仅掌握概念，而且知晓它的理论数据.2.提倡学生进行自学，并能与同学互相交流与合作，变学会知识为会学知识.3.培养学生的求同和求异思维，能从相似的事物中观察到P X 们的共同点和不同点.(三)情感与价值观要求通过学生在学习中互相帮助、相互合作，并能对不同概念进行区分，培养大家的团队精神，以及认真仔细的学习态度，为学生将来走上社会而做准备，使他们能在工作中保持严谨的态度，正确处理好人际关系，成为各方面的佼佼者.学习重点：1.了解平方根、开平方的概念.2.了解开方与乘方是互逆的运算，会利用这个互逆运算关系求某些非负数的算术平方根和平方根.3.了解平方根与算术平方根的区别与联系.学习难点：1.平方根与算术平方根的区别与联系.2.负数没有平方根，即负数不能进行开平方运算的原因.预习.导学1、上节课我们学习了算术平方根的概念，性质.知道若一个正数x的平方等于a，即x2=a.则x叫a的算术平方根，记作x=，而且也是非负数，比如正数22=4，则2叫4的算术平方根，4叫2的平方，但是(－2)2=4，则－2叫4的什么根呢？下面我们就来讨论这个问题.2、.平方根、开平方的概念3、请大家先思考两个问题.(1)9的算术平方根是3，也就是说，3的平方是9，还有其他的数，它的平方也是9吗？(2)平方等于的数有几个？平方等于0.64的数呢？4、根据上一节课的内容，我们知道了是9的算术平方根，是的算术平方根，那么－3，－叫9、的什么根呢？请大家认真看书后回答.5、由平方根和算术平方根的定义。

6、平方根的性质，请大家思考以下问题.(1)一个正数有几个平方根.(2)0有几个平方根?(3)负数呢？7、什么叫开平方呢？8、平方根与算术平方根的联系与区别学习过程：［例］求下列各数的平方根.(1)64； (2)； (3)0.0004； (4)(－25)2； (5)11.想一想(1)()2等于多少？()2等于多少？(2)()2等于多少？(3)对于正数a，()2等于多少？课堂练习(一)随堂练习1.求下列各数的平方根1.44，0，8，，441，196，10－42.填空(1)、25的平方根是_________；(2)、 =_________；(3)、()2=_________.（4）、如果x2=a,(x为正数)那么x叫做__________________.(5)、| 2 |的算术平方根是_________,0算术平方根是__________.(6)、9的平方是_________,9的平方根是__________,—9是______的一个平方根，（—4）2的平方根是___________.7）、平方根等于它本身的数是____________,算术平方根等于它本身的数有_________________,作业：P42习题2.4 1、3、4。