周长解决问题例5
- 格式:ppt
- 大小:1.28 MB
- 文档页数:12

人教版数学三年级上册教案长方形和正方形的周长(解决问题例5)教学内容:(三年级上册)第86页内容教学目标:1、使学生巩固应用周长的含义,探索并发现长方形、正方形周长计算的方法。
2、培养学生观察、推理、分析、综合、抽象、概括的能力和解决简单的实际问题的能力。
3、培养学生积极探究、大胆尝试的自主学习能力和同学间协作互助的精神。
教学重点:长方形、正方形的周长的计算方法。
教学难点:能灵活运用所学知识解决生活中的实际问题。
教学方法:让学生自主探索解决问题,经历探究的全过程。
放手让学生运用知识迁移自主探究,解决问题。
教学用具:课件等。
教学过程:一、创设情境、激发兴趣上节课,我们学习了有关求周长的知识,哪个同学愿意到前面来举例说说怎样求正方形的周长和长方形的周长?出示长方形和正方形课件。
二、合作学习,自主探究2、出示例5(长方形课件)用16张边长1分米的正方形纸拼长方形和正方形,怎样拼,才能使拼成的图形周长最短?(1)教师帮学生读题,理清题意,明确要求的问题。
(2)学生小组合作,动手拼摆。
(3)全班交流所拼的图形及周长是多少?最后确定怎样拼成的图形最短。
共有三种拼法。
方法一:摆一排,共摆16个,周长是34分米;方法二:摆两排,每排摆8个,周长是20分米;方法三:摆四排,每排摆4个,周长是16分米。
答案:拼成正方形的最短。
(4)通过这个例题的学习,你发现了什么?小结:面积一定,长和宽越接近,周长越短。
三、巩固运用,深化拓展1、完成教材第86页“做一做”2、在一块长是8厘米,宽是5厘米的铁板上剪下一个最大的正方形,这个正方形的周长是多少?3、完成教材第87页第4题。
四、课堂小结板书设计长方形和正方形的周长解决问题长方形的周长=(长+宽)×2正方形的周长=边长×4面积一定,长和宽越接近,周长越短教学反思:这节课改变学生的学习方式,运用合作学习,培养学生的协作能力。
教学设计时,教师遵循学生学习数学的心理规律,强调从学生已有的知识和生活经验出发,让学生经历自主探索、合作交流的过程。


F ocus on Subjects 学科专辑/ “强化学生数学思维训练”研究专辑 41维瓶颈,贯通整体解决思路,形成较为完整的解决方 案,让成功思考成为可能的现实。
【案例4】苏教版四下“射线&直线和角的认识”预习案1. 留心观察生活$搜集一些有关射线、直线、角的图片或实例&2. 自学课本第77〜78页,尝试完成’想想做做(第1题&3. 我来动动手&在横线上画一条2厘米的线段: ________在横线上画一条3厘米的射线: ________在横线上画一条4厘米的直线:________我的发现:_______________我对射线、直线的理解是:_______________4. 我的其他收获:__________________友情提示:如果感到有困难,可以请教老师或家长,也可以和小伙伴们商量。
师:老师课前请大家画了一条2厘米的线段(画好 了吗?是这样的吗?(展示一位同学的作V )。
师:你是怎样画的呀?(及时提炼学生发言:直直的,有两个端点,用尺量长度等)师:这是一支激光笔,如果把发光点看成是一个端点,(将激光射到天花板上)现在,你在天花板上 看到了 ?(另一个光点)师:如果把这两个光点用一条直直的线连接起来, 就得到一条?(线段)师:现在,老师把激光笔射出的红色光线射向天 空,你还能找到光线尽头的那个光点吗?(不能)师:那这条线是直的吗?有几个端点? 量出 长度吗?先独立想一想,再和同学议一议,(反馈略)师小结:这条线只有一个端点,是直直的,:长,学上为射线。
师(出示一位同学的预习案):我们可以画出一条 长3厘米的射线吗?教师课前让学生画线段、射线、直线,将学生对 线段、射线、直线长度的元认知充分放大,再通过课堂小组活动碰撞、质疑、交流,教师对学生的疑难之 处及时点拨,让学生在观察、思考的基础上深入体会"直线两端可以无限地延长”"射线一端可以无限地延 长”的具体涵义,尽量给出充足的时间让学生用“没 有尽头”这样的儿童语言对新知做出自己的描述。


面积与周长的应用问题在数学中,面积和周长是与形状相关的重要概念,广泛应用于各个领域。
无论是在家庭日常生活中还是在工程建设中,我们都会遇到各种与面积和周长相关的实际问题。
本文将通过几个实例,探讨面积和周长在实际问题中的应用。
一、花坛设计假如你有一个庭院,你想在其中设计一个花坛。
你已经决定花坛的形状为长方形,但是你还需要确切的尺寸以便购买足够的土壤和植物。
这时候,面积和周长的概念就显得尤为重要。
首先,我们需要测量庭院的可用空间,并决定花坛的长度和宽度。
假设庭院的长为10米,宽为5米,我们可以计算出花坛的面积为长乘以宽,即10米乘以5米,得到50平方米。
接下来,我们可以计算花坛的周长。
长方形的周长等于两倍的长加两倍的宽。
在这个例子中,周长等于两倍的10米再加上两倍的5米,即20米加10米,得到30米。
通过计算花坛的面积和周长,我们可以更好地了解所需的土壤和植物数量,以便在家庭庭院中进行合理的花坛设计。
二、围栏材料计算假设你要围起一个矩形花园,并且你需要购买围栏材料。
在这种情况下,你需要考虑花园的周长来确定需要购买多少材料。
假设花园的长为8米,宽为6米。
我们可以使用周长的概念来计算所需的围栏材料数量。
矩形的周长等于两倍的长加两倍的宽。
在这个例子中,周长等于两倍的8米再加两倍的6米,即16米加12米,得到28米。
这意味着你需要购买28米的围栏材料来围起这个花园,并确保它是完全封闭的。
通过计算周长,我们可以准确估计所需的材料量,以便在购买过程中不会出现材料不足或材料浪费的情况。
三、地板铺设面积和周长的概念在地板铺设中也非常重要。
想象一下,你想在一个正方形房间中铺设地板,你需要知道房间的面积以便购买适当数量的地板。
假设房间的边长为4米,我们可以使用面积的概念来计算所需的地板面积。
正方形的面积等于边长的平方。
在这个例子中,面积等于4米乘以4米,即16平方米。
这意味着你需要购买16平方米的地板来完全铺满这个房间。


六年级数学上册典型例题系列之第五单元圆的周长问题提高部分(解析版)编者的话:《六年级数学上册典型例题系列》是基于教材知识点和常年考点考题总结和编辑而成的,其优点在于选题典型,考点丰富,变式多样。
本专题是第五单元圆的周长问题提高部分,后续内容为《圆的面积问题基础部分》。
本部分内容是在《圆的周长问题基础部分》内容基础上进行总结和编辑的,其内容主要以求不规则图形的周长为主,多考察图形题,综合性较强,题目难度较大,建议作为重点部分讲解,共划分为四个考点,欢迎使用。
【考点一】圆周长的比较问题。
【方法点拨】圆周长的比较问题,如果小圆直径之和与大圆直径相等,那么周长相等。
【典型例题】小乌龟和小白兔又要比赛了,这一次小白兔沿大圆跑一圈,小乌龟沿两个小圆“∞”跑一圈,谁跑的路程长呢?好好想一想。
解析:看图可知:两个小圆的直径和等于大圆的直径。
设小圆的直径为 1 米,则大圆的直径为 2米,分别求出两个小圆的周长和与一个大圆的周长,再比较路程长短。
解: 3.14×2=6.28(米)3.14×1×2=6.28(米)答:小乌龟和小白兔跑的路程同样长。
【典型例题2】观察如图两个图形中的阴影部分,周长和面积大小关系是()A.周长相等,面积不相等 B.周长和面积都相等C.周长不相等,面积相等 D.周长和面积不相等解析:C【对应练习1】大圆内有两个小圆,大圆的周长与两个小圆的周长之和相比()A.大圆周长长 B.同样长 C.两个小圆周长之和长 D.无法确定解析:B【对应练习2】如下图所示,要从A点到B点,沿大圆走比较近还是沿小圆走比较近()。
A.大圆B.小圆C.一样近解析:C【对应练习3】如图所示,从A到B的路线中,()。
A.第①条路长B.第②条路长C.一样长D.无法判断解析:C【考点二】较简单的不规则图形的周长。
【方法点拨】求不规则图形的周长,寻找该图形是由那些边组合而成的,将这些边的长度相互加起来,注意观察弧形是否可以组合一起构成半圆或整圆。

周长应用题
周长应用题是数学中常见的一类题目,主要涉及到计算各种形状(如长方形、正方形、三角形等)的周长。
周长是指一个平面图形所有边的长度之和。
以下是一些周长应用题的示例:
长方形周长应用题:
一个长方形镜框的长是2米,宽是1米。
用一条长7米的花边能绕镜框一周吗?多多少米?
一个长方形操场,长100米,宽65米。
小强围着操场跑了2圈,他一共跑了多少米?
正方形周长应用题:
一个正方形的边长是8厘米,如果把它的边长增加10厘米,那么它的周长增加多少厘米?
三角形周长应用题:
一个三角形的周长是30米,其中一条边是10米,另一条边是15米,求第三条边的长度。
组合图形周长应用题:
有两个同样的长方形,长是8分米,宽是4分米。
如果把它们拼成一个正方形,这个正方形的周长是多少分米?
把一张长36厘米,宽18厘米的长方形纸片,剪成两个正方形,其中一个正方形的周长是多少厘米?
解决周长应用题的一般步骤包括:
确定图形的类型(长方形、正方形、三角形等)。
识别图形各边的长度。
应用周长公式进行计算。
例如,长方形的周长 = (长 + 宽) ×2;正方形的周长 = 边长× 4;三角形的周长 = 三条边之和。
根据题目要求,进行必要的单位换算或比较。
通过练习这些应用题,可以提高数学计算能力和空间想象能力。


圆(一)圆的周长知 知识梳理1、圆的周长:围成圆的曲线的长度叫做圆的周长。
用字母C 表示。
2、圆周率实验:在圆形纸片上做个记号,与直尺0刻度对齐,在直尺上滚动一周,求出圆的周长。
得到结论:发现一般规律,就是圆周长除以它直径的商是一个固定数(π)。
3、圆周率:任意一个圆的周长与它的直径的比值(或商)是一个固定的数,我们把它叫做圆周率。
用字母π(pai )表示。
(1)一个圆的周长总是它直径的3倍多一些,这个比值是一个固定的数。
(2)圆周率π是一个无限不循环小数。
在计算时,一般取14.3≈π。
(3)在判断时,圆周长与它直径的比值是π倍,而不是3.14倍。
(4)世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
4、圆的周长公式:C=πd 或C=2πr 圆周长=π×直径 圆周长=π×半径×25、区分周长的一半和半圆的周长:(1)周长的一半:等于圆的周长÷2. 计算方法:即 (2)半圆的周长:等于圆的周长的一半加直径. 计算方法:即5.14r.6、当一个圆的半径增加a厘米时,它的周长就增加2πa厘米;当一个圆的直径增加a厘米时,它的周长就增加πa厘米。
7、常用的3.14计算典题探究例1 填空(1)画圆时,圆规两脚间的距离就是圆的( )。
(2)圆无论大小,它的周长总是直径的( )倍多一些,我们叫它做( ),用字母( )表示。
(3)( )确定圆的位置,( )确定圆的大小。
(4)一个圆的直径扩大2倍,它的半径扩大( )倍,它的周长扩大( )倍。
(5)圆的周长扩大6倍,它的半径就扩大( )倍例2 看图填空。
(单位:厘米)(1)圆的半径是( ); (2)圆的直径是( ); (3)圆的直径是( );长方形的宽是( ). 正方形的边长是( ). 三角形的边长是( ).例3①一捆电线绕了9圈,每圈直径都是48厘米,这捆电线长( )米.②在边长4厘米的正方形中画一个最大的圆,圆的周长是( )厘米.③两个圆半径的和12厘米,一个圆直径10厘米,另一个圆的周长是( )厘米.例4 挂钟分针的针尖在41小时内,正好走了25.12厘米。
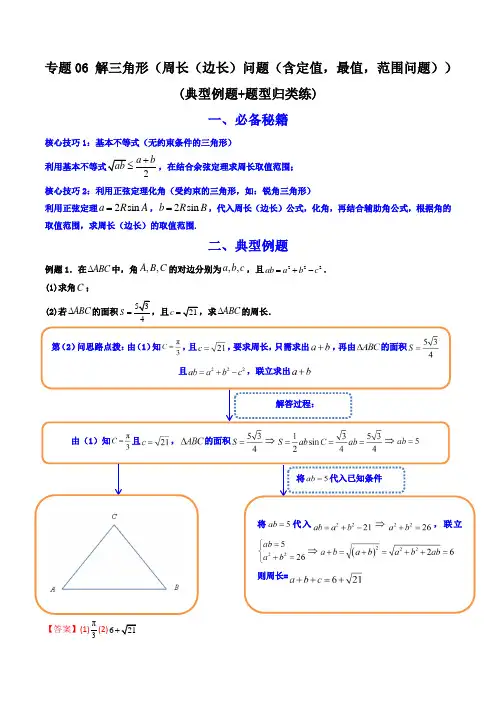
专题06 解三角形(周长(边长)问题(含定值,最值,范围问题))(典型例题+题型归类练)一、必备秘籍核心技巧1:基本不等式(无约束条件的三角形) 利用基本不等式2a bab +≤,在结合余弦定理求周长取值范围; 核心技巧2:利用正弦定理化角(受约束的三角形,如:锐角三角形)利用正弦定理2sin a R A =,2sin b R B =,代入周长(边长)公式,化角,再结合辅助角公式,根据角的取值范围,求周长(边长)的取值范围.二、典型例题例题1.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且222ab a b c =+-. (1)求角C ; (2)若ABC ∆的面积534S =,且21c =,求ABC ∆的周长.【答案】(1)π3(2)621+第(2)问思路点拨:由(1)知,且,要求周长,只需求出,再由的面积且,联立求出解答过程:由(1)知且,的面积将代入,联立则周长=将代入已知条件(1)因为222ab a b c =+-,由余弦定理,得到2221cos 22a b c C ab +-==,又0πC <<,所以π3C =; (2)因为△ABC 的面积534S =,且21c =,π3C =所以有221353sin 21244S ab C ab ab a b ====+-,, 联立22526ab a b =⎧⎨+=⎩,则()22226a b a b a b ab +=+=++=,所以△ABC 的周长为621a b c ++=+例题2.已知ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且sin sin ()sin b B a A b c C -=-. (1)求角A 的大小; (2)若ABC 的面积2534ABCS =,且5a =,求b c +的值.【答案】(1)3π(2)10 第(2)问思路点拨:由(1)知,且,要求,可利用面积公式求出,再由余弦定理求出,联立,可求出解答过程:由(1)知且将代入,联立则将代入已知条件(1)解:因为sin sin ()sin b B a A b c C -=-,由正弦定理可得22()b a b c c -=-,即222a b c bc =+-,即222b c a bc +-=, 由余弦定理可得2222cos a b c bc A =+-,故2221cos 222b c a bc A bc bc +-===,因为()0,A π∈,所以3A π=.(2)解:因为n 2534113si 222ABCbc SA b c ==⨯=⨯⨯,所以25bc =, 再由222a b c bc =+-,即2225=+-b c bc ,所以2250b c +=, 所以()222210b c b c b c bc +=+=++=.例题3.在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知3,3a A π==.(1)若5sin 13B =,求sinC ; (2)求b c +的最大值.【答案】(1)123526+(2)23 第(2)问思路点拨:由(1)知,且,要求的最大值,可优先考虑余弦定理+基本不等式解答过程:由(1)知且,由余弦定理对使用基本不等式两边同时加上2()b c +2223()3()()4b c bc b c b c +-≥+-+⇒213()4b c ≥+23b c +≤,当且仅当3b c ==时,等号成立(1)∵3sin 2A =∵5sin sin 13B A =<,∴2B A π<<,∴3os 1c 12B =所以312151235sin sin()21321326C A B +=+=⨯+⨯=. (2)在ABC 中由余弦定理可知2222232cos a b c bc A b c bc ==+-=+-∴223()()333234b c b c bc b c ++=+≤+⇒+≤当且仅当3b c ==时,b c +的最大值为23.例题4.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且22cos cos 2cos b a A C c A =+. (1)求角A ;(2)若4a =,求2c b -的取值范围.【答案】(1)3π(2)()8,4- (1)解:因为22cos cos 2cos b a A C c A =+,第(2)问思路点拨:由(1)知,且,要求的取值范围,注意到连接符号是“”,并且,前系数不一致,基本不等式不能直接解决问题,考虑利用正弦定理化角.解答过程:由(1)知且,由正弦定理.,化角,求范围先拆,后合(辅助角公式)因为,所以由正弦定理得2sin 2sin cos cos 2sin cos B A A C C A =+, 即()sin 2cos sin cos sin cos B A A C C A =+, 即()sin 2cos sin B A A C =+,因为πA B C ++=,所以πA C B +=-, 所以sin 2cos sin B A B =.因为()0,πB ∈,所以sin 0B ≠, 所以1cos 2A =,因为()0,πA ∈,所以3A π=.(2)解:由正弦定理得sin a A =所以)2sin 2sin sin 2s ππin 3c b C B B B ⎤⎛⎫--=--- ⎪⎥⎝⎭⎣⎦3ππsin 8cos cos cos sin 233B B B B ⎫⎛⎫-=-⎪ ⎪⎪⎝⎭⎝⎭, 所以π28cos 3c b B ⎛⎫-=+ ⎪⎝⎭.因为2π0,3B ⎛⎫∈ ⎪⎝⎭,所以,ππ33πB ⎛⎫+∈ ⎪⎝⎭,所以1cos 1,32πB ⎛⎫⎛⎫+∈- ⎪ ⎪⎝⎭⎝⎭,所以()28,4c b -∈-.例题5.在ABC 中,内角,,A B C 所对的边分别为,,a b c ,且sin sin 2B Cb a B +=. (1)求A 角的值;(2)若ABC 为锐角三角形,利用(1)所求的A 角值求a cb-的取值范围.【答案】(1)3A π=(2)3132,2⎛⎫-- ⎪ ⎪⎝⎭(1)因为sinsin 2B C b a B +=,所以sin cos sin sin 2AB A B =, 第(2)问思路点拨:由(1)知,且为锐角三角形,要求的取值范围,不适合直接利用基本不等式解决问题,当涉及到有约束条件的三角形(锐角三角形)优先考虑利用正弦定理化角.解答过程:直接化角由(1)知,(注意到,统一化成一个角)(注意到此时分子分母都含有角,不容易直接求范围)先拆,后合(辅助角公式),化简化半角,继续化简,直到角,函数名统一,即,∴∴的取值范围是.(角,函数名统一,问题转化为求的取值范围)求取值范围 求取值范围因为()0,B π∈,∵sin 0B ≠, ∴cos2sin cos 222A A A =,∵(0,)A π∈,∴cos 02A ≠,∴1sin 22A =,因为022A π<<,∴26A π=,∴3A π=. (2)由正弦定理,2sinsin sin sin 33sin sin B a c A Cb BBππ⎛⎫-- ⎪--⎝⎭==331cos sin 31cos 1222sin s2in 2B BB B B ---==⋅- 2112sin 31312tan 222222sin cos 22B B B B ⎛⎫-- ⎪⎝⎭=⋅-=-,∵ABC 为锐角三角形,∴62B ππ<<,即1224B ππ<<,23tan 12B-<<, ∴313132tan 2222B --<-<} ∴a cb -的取值范围是3132,2⎛⎫-- ⎪ ⎪⎝⎭.例题6.已知ABC ∆的内角,,A B C 所对的边分别是,,a b c ,()()()sin sin sin a b A B a c C +-=-. (1)求角B ;(2)若ABC ∆外接圆的周长为23π,求ABC ∆周长的最大值.第(2)问思路点拨:由(1)知,且外接圆的周长为,可求出外接圆直径要求周长的最大值,由于三角形不受约束,可优先考虑基本不等式.【答案】(1)3B π=(2)9(1)由正弦定理可得()()()a b a b a c c +-=-,即222ac a c b =+-.由余弦定理得2221cos 22a c b B ac +-==. 又()0,B π∈,所以3B π=.(2)因为△ABC 外接圆的周长为,所以△ABC 外接圆的直径为由正弦定理得sin b B =3b ==.由余弦定理得2292cos a c ac B =+-. 因为()()223934a c ac a c +=+-≤⨯,所以()2194a c +≤,即6a c +≤,由三角形性质知36a c <+≤,当且仅当a c =时,等号成立.所以69a b c <++≤故△ABC 周长的最大值9. 例题7.已知ABC 的内角,,A B C 的对边分别为,,a b c ,且(cos cos )a b c B A -=-. (1)判断ABC 的形状;(2)若a b ≠,4c =,求ABC 周长的取值范围.【答案】(1)直角三角形或等腰三角形(2)(8,442)+ (1)ABC 为等腰三角形或直角三角形,证明如下:由()cos cos a b c B A -=-及正弦定理得,()sin sin sin cos cos A B C B A -=-, 即()()()sin sin sin cos cos B C A C C B A +-+=-,第(2)问思路点拨:由(1)知,由(1)及知为直角三角形且不是等腰三角形,要求周长的取值范围,有约束条件下,建议优先考虑利用正弦定理化角求范围.解答过程:由(1)及知为直角三角形且不是等腰三角形,且,故,且周长可表示为:利用余弦定理化角;根据的取值范围,求出的范围因为,故,得,所以,所以周长的取值范围为.即sin cos cos sin sin cos cos sin sin cos sin cos B C B C A C A C C B C A +--=-, 整理得sin cos sin cos 0B C A C -=,所以()cos sin sin 0C B A -=, 故sin sin A B =或cos 0C =,又A 、B 、C 为ABC 的内角,所以a b =或2C π=,因此ABC 为等腰三角形或直角三角形.(2)由(1)及a b ≠知ABC 为直角三角形且不是等腰三角形, 且2A B π+=,2C π=故2A B π=-,且4B π≠,ABC周长44(cos sin )444a b c a b B B B π⎛⎫=++=++=++=++ ⎪⎝⎭,因为0,,442B πππ⎛⎫⎛⎫∈⋃ ⎪ ⎪⎝⎭⎝⎭,故3,,44224B πππππ⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭,得sin 4B π⎫⎛⎫+∈⎪ ⎪⎪⎝⎭⎝⎭,所以()48,44B π⎛⎫++∈ ⎪⎝⎭, 所以ABC 周长的取值范围为()8,4.三、题型归类练1.ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知(2)sin (2)sin 2sin a c A c a C b B -+-=. (1)求B ;(2)若ABC 为锐角三角形,且2c =,求ABC 周长的取值范围. 【答案】(1)π3B =;(2)(3+.(1)在ABC 中,由正弦定理及(2)sin (2)sin 2sin a c A c a C b B -+-=得:2(2)(2)2a c a c a c b -+-=,整理得:222a cb ac +-=,由余弦定理得:2221cos 22a cb B ac +-==,而0πB <<,解得π3B =,所以π3B =.(2)由(1)知2π3A C +=,即2π3A C =-,因ABC 为锐角三角形,即2ππ032π02C C ⎧<-<⎪⎪⎨⎪<<⎪⎩,解得ππ62C <<,由正弦定理sin sin sin a b cA B C ==得:sin sin sin sina b c c A BC C++=++, 则22π23sin()sin ]sin )sin 3sin 2a b c C C C C C C ++=-+=+)22cos1cos2333sin2sin cos tan222CCC CC+=+=+=,当ππ62C<<时,ππ1224C<<,ππtan tan tan1224C<<,而tan tanπ34tan tan()212341tan tan34ππππππ-=-===+即2tan12C<,因此,112tan2C<<36a b c++<+,所以ABC周长的取值范围是(3+.2.请从下面的三个条件中任选一个,补充在下面的横线上,并解答.①3cos22cos()02C A B+++=;②ABC的面积为1(sin sin sin)2c a A b B c C+-;③221cos2a c Bbc b⎛⎫-=-⎪⎝⎭. 在ABC中,内角A,B,C的对边分别为a,b,c,若___________.(1)求角C;(2)若0c AB BC=⋅≥,求a b+的取值范围.【答案】(1)π3C=(2)(1)选①,3cos22cos()02C A B+++=,得232cos12cos02C C--+=得1cos2C=,而C为三角形内角,故π3C=,选②,11sin(sin sin sin)22ABCS ab C c a A b B c C==+-,由正弦定理化简得223abc ca b c c=+-,得2221cos22a b cCab+-==,而C为三角形内角,故π3C=,选③,由221cos2ac B ab c b-=-,即2222211()22a cb abc b+--=-,得2221cos22a b cCab+-==,而C为三角形内角,故π3C=,(2)由(1)知π3C=,故2sin sin sina b cA B C===,故2ππ2sin2sin2sin()2sin3sin)36a b A B B B B B B+=+=-+=+=+,而0AB BC⋅≥,故cos0B≤,π2π[,)23B ∈,π2π5π[,)636B +∈,a b +∈3.在△ABC 中,内角A B C 、、的对边分別为1cos 2a b c b C a c -=-,,, ,(1)求B ;(2)设b =△ABC 的周长的取值范围;.【答案】(1)π3B =(2)((1)由余弦定理知222cos 2a b c C ab +-=,所以222122a b c b a c ab +-⨯-=-,整理得222a cb ac +-=,所以2221cos 22a cb B ac +-==,因为()0,πB ∈,所以π3B =;(2)由(1)知()()()22222223324a c a c b a c ac a c ac a c ++⎛⎫=+-=+-≥+-= ⎪⎝⎭, 当且仅当a c =时,等号成立.因为b =()212a c +≤,即a c +≤又因为a c b +>=a c <+≤所以a b c <++≤所以ABC 的周长的取值范围是(;综上,π3B =,ABC 的周长的取值范围是(.4.在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知()()cos cos cos A A B A B =+. (1)求角B 的大小;(2)若1a c +=,求b 的取值范围. 【答案】(1)3π(2)1,12⎡⎫⎪⎢⎣⎭(1)∵()()cos cos cos A A B A B =+, ∴cos cos cos cos()A B A B A B -=+,即cos cos cos cos cos sin sin A B A B A B A B =-, ∵sin 0A ≠, ∴tan B =∵()0,B π∈,∴3B π=.(2)由余弦定理可知2222cos b a c ac B =+-,代入可得22222()3132a c b a c ac a c ac +⎛⎫=+-=+-≥-⨯ ⎪⎝⎭2111324⎛⎫=-⨯= ⎪⎝⎭,当且仅当12a c ==时取等号,∴12b ≥,又1b ac <+=, ∴b 的取值范围是1,12⎡⎫⎪⎢⎣⎭.5.记锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且()2πcos3cos 4cos 1,3a Bb A B B =-<. (1)求AB的值; (2)求ab的取值范围.【答案】(1)3AB=(2)()1 (1)由题意得2sin cos3sin cos (cos 22cos )A B B A B B =+cos (sin cos 2cos sin 2)cos sin3A B B B B A B =+=,得sin cos3cos sin3sin(3)0A B A B A B -=-=, 因为A ,B 都是三角形内角,3B π<,所以3A B =,即3AB=; (2)由(1)得24cos 1aB b=-, 因为△ABC 为锐角三角形,所以03203042A B B C B ππππ⎧<=<⎪⎪⎪<<⎨⎪⎪<=-<⎪⎩,得86B ππ<<, 因为2cos2cos 148ππ=-,所以24cos 2cos2284ππ=+=所以2224cos124cos 14cos 1168B ππ-=-<=<-,故ab的取值范围为()1; 综上,3,A B = ab的取值范围为()1. 6.设ABC 是锐角三角形,内角,,A B C 所对的边分别为,,a b c,且π,3A a ==(1)求证:bc 的最大值是3; (2)求b c +的取值范围.【答案】(1)证明见解析;(2)(3,. (1)由余弦定理知:22221322b c bc b c bc =+-⋅=+-, 所以223b c bc =+-2bc bc bc ≥-=即3bc ≤,当且仅当b c ==且此时ABC 是锐角三角形,所以bc 的最大值是3; (2)由正弦定理得2sin b B =,2π12sin 2sin()sin )32c C B B B ==-=+31π2(sin )cos )sin()226b c B B B B B +=+=+=+ABC 是锐角三角形π0ππ22ππ62032B B C B ⎧<<⎪⎪⇔⇔<<⎨⎪<=-<⎪⎩ππ2πππsin()13)36366B B B ⇔<+<⇒<+≤⇔<+≤, 所以b c +的取值范围是(3,.7.在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,设()1,m a =,()3sin ,cos n C b a C =-,//m n .(1)求角A ; (2)求bc 的取值范围.【答案】(1)6A π=(2)b c ∈⎝⎭(1)由//m n 得到cos sin ba C C -, ∴sin sin cos sinB AC A C -=, ∴sin()sin cos sin A CA C A C +-=,即sin cos cos sin sin cos sin A C A CA C A C +-=, ∴cos sin sin A C A C ,又C 为三角形内角,故sin 0C ≠,∴cos A A =,故tan A =,∴6A π=.(2)sin sin b Bc C=,∵6A π=,∴51sin cos sin 1622sin sin sin 2tan C C Cb Bc C C C Cπ⎛⎫- ⎪⎝⎭====, 又∵ABC 是锐角三角形,∴0,2B π⎛⎫∈ ⎪⎝⎭且0,2C π⎛⎫∈ ⎪⎝⎭,即5062C ππ<-<且02C <<π,∴32C ππ<<,∴tan C >∴12tan C <<b c ∈⎝⎭. 8.已知,,a b c 分别为ABC 三个内角,,A B C 的对边,()(),,1,cos m a b c n C C =+=,且m n ∥, (1)求A ;(2)若4a =,求b c +的取值范围. 【答案】(1)π3A =(2)(]4,8(1)由题意得:cos sin 0a C C b c --=,由正弦定理得:sin cos sin sin sin 0A C A C B C --=, 因为()sin sin sin cos cos sin B A C A C A C =+=+,sin cos sin sin 0A C A C C --=, 因为()0,πC ∈,所以sin 0C ≠,cos 1A A -=,即π2sin 16A ⎛⎫-= ⎪⎝⎭,π1sin 62A ⎛⎫-= ⎪⎝⎭因为()0,πA ∈,所以ππ5π,666A ⎛⎫-∈- ⎪⎝⎭, 所以ππ66A -=,π3A =(2)因为4a =,所以由正弦定理得:4πsin sin sin sin3b c a B C A ====,)πsin sin sin sin 3b c B C C C ⎤⎛⎫+=+=++ ⎪⎥⎝⎭⎣⎦1πsin sin 8sin 26C C C C ⎫⎛⎫++=+⎪ ⎪⎪⎝⎭⎝⎭, 因为2π0,3C ⎛⎫∈ ⎪⎝⎭,所以ππ5π,666C ⎛⎫+∈ ⎪⎝⎭,所以(]π8sin 4,86C ⎛⎫+∈ ⎪⎝⎭,b c +的取值范围是(]4,89.ABC 的内角A 、B 、C 所对边的长分别为a 、b 、ccos sin B b C =+. (1)求C 的大小;(2)若ABC为锐角三角形且c =22a b +的取值范围. 【答案】(1)3C π=(2)(5,6](1)cos sin B b C +及正弦定理可得sin sin sin )B C B C A B C +==+cos sin B C B C =,所以sin sin cos B C B C =,因为B 、(0,)C π∈,则sin 0B >sin 0C C =>,则tan C =3C π=.(2)依题意,ABC为锐角三角形且c =2sin sin sin a b cA B C====, 所以2sin a A =,2sin 2sin()2sin 3b B A C A π⎛⎫==+=+ ⎪⎝⎭,所以222221cos 21cos 234sin 4sin 44322A A a b A A π⎛⎫-+ ⎪π-⎛⎫⎝⎭+=++=⨯+⨯⎪⎝⎭142cos 2222cos 222c 2cos 222os 23A A A A A ⎛⎫=---π⎛⎫=-+-+ ⎪⎝⎭ ⎪ ⎪⎝⎭2c 42co os 242sin 246s 2cos 22A A A A A A π⎛⎫=-+=-=- ⎝+⎪⎭+,由于23A B π+=,所以022032A A πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,解得62A ππ<<,所以23A ππ<<,52666A πππ<-<,所以1sin 2,162A π, 所以2sin 2(1,2]6A π⎛⎫-∈ ⎪⎝⎭,所以2sin 24(5,6]6A π⎛⎫-+∈ ⎪⎝⎭.所以22a b +的取值范围是(5,6].10.已知ABC 的内角A ,B ,C 的对边分别为a ,b ,c 222cos a b C A bc--=(1)求角B 的大小;(2)若B为钝角,ABC 为等腰三角形,且BC ABC 的周长.【答案】(1)3B π=或23π(2)4+(1)2222222b c a a b C bc bc +---⨯=cC b=,sin sin CC B=,因为()0,C π∈,所以sin 0C ≠,所以sin B =,0B π<<,即3B π=或23π(2)设等腰三角形腰长为x , 即==AB BC x ,12CM x =,且由于6A C π==,23B π=,在ABC 中,222cos 2x x AC B x x+-=⨯⨯,解得AC =,在ACM △中,由余弦定理得:2222cos AM AC CM AC CM C =+-⋅⋅,即)22213742x x =+-,解得:2x =,所以2AB BC ==,AC =则ABC 的周长:4+11.已知ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且3b =,cos 2cos()B A C =+. (1)求B ;(2)求ABC 周长的取值范围. 【答案】(1)π3;(2)(6,9].(1)在ABC 中,22cos 1cos(π)B B -=-,即22cos cos 10B B +-=,解得1cos 2B =,而0πB <<, 所以π3B =.(2)在ABC 中,由余弦定理得:2222222192cos ()3()3()()24a cb ac ac B a c ac a c a c +==+-=+-≥+-=+, 当且仅当a c =时取“=”,即有06a c <+≤,因此,当3a c ==时,max ()6a c +=,而3a c b +>=,即36a c <+≤,69a b c <++≤, 所以ABC 周长的取值范围是(6,9].12.设ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且sin sin sin sin b B a A b A c C +=+. (1)求角C ;(2)若c =,求a b +的取值范围.【答案】(1)3C π=(2)((1)解:由正弦定理sin sin sin a b cA B C==及sin sin sin sin b B a A b A c C +=+,所以222b a ab c +=+.所以由余弦定理得2221cos 22a b c C ab +-==,又()0,C π∈,所以3C π=.(2)解:因为c =,3C π=,由余弦定理可得2221cos 22a b c C ab +-==,可得()2212a b ab ab +--=,所以()2212332a b a b ab +⎛⎫+-=≤ ⎪⎝⎭,()2124a b +≤,可得a b +≤a b =时取等号,又由三角形三边关系得a b c +>=所以a b +的取值范围是(.13.已知ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且sin cos()6b Cc B π=-.(1)求角B ;(2)若b =4,求ABC 周长的最大值. 【答案】(1)3B π=;(2)12.(1)因为sin cos()6b C c B π=-,则1sin sin )2b Cc B B =+,在ABC 中,由正弦定理得,1sin sin sin sin )2B C C B B =+,而(0,π)C ∈,即sin 0C >,整理得sin B B ,即tan B =()0,πB ∈,解得π3B =, 所以π3B =. (2)在ABC 中,由余弦定理2222cos b a c ac B =+-得:2216a c ac =+-,即()2163a c ac +-=, 而2()2a c ac +≤,于是得()264a c +≤,当且仅当a =c =4时取“=”, 因此,当a =c =4时,a +c 取最大值8,从而a +b +c 取最大值12, 所以ABC 周长的最大值为12.14.在ABC 中,sin 2C C =. (1)求C ∠;(2)若6b =,且ABC 的面积为ABC 的周长. 【答案】(1)6π(2)663(1)解:因为()0,C π∈,则sin 0C >2sin cos C C C =,可得cos C =,因此,6C π=.(2)解:由三角形的面积公式可得13sin 22ABCSab C a ===,解得a =由余弦定理可得2222cos 48362612c a b ab C =+-=+-⨯=,c ∴=所以,ABC 的周长为6a b c ++=.15.在ABC 中,角,,A B C 的对边分别为,,a b c ,且sin cos a B A =. (1)求角A ;(2)若a =1b =,求ABC 的周长.【答案】(1)3A π=(2)3(1)由正弦定理得:sin sin cos A B B A =,()0,B π∈,sin 0B ∴≠,sin A A ∴=,则tan A = 又()0,A π∈,3A π∴=. (2)由余弦定理得:22222cos 12cos33a b c bc A c c π=+-=+-=,即220c c --=,解得:1c =-(舍)或2c =,ABC ∴的周长为3a b c ++=16.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .在①2cos cos c b aB A-=;②cos 2cos cos c A b A a C =-;③cos cos 2cos cos b C c B a A A -=cos cos 2cos cos b C c Ba A A-=这三个条件中任选一个补充在下面的问题中,并解答. (1)若 ,求A ;(2)在第(1)问的前提下,若1a =,求△ABC 的周长的取值范围. 注:如果选择多个条件分别解答,按第一个解答计分. 【答案】(1)条件选择见解析,3A π=(2)(]2,3(1)选①. 由2cos cos c b a B A -=及正弦定理得2sin sin sin cos cos C B A B A-=, ∴()2sin sin cos sin cos C B A A B -⋅=,∴()2sin cos sin cos cos sin sin sin C A A B A B A B C =+=+=, 由于△ABC 中,sin 0C ≠,()0,A π∈,∴2cos 1A =,即1cos 2A =, ∴3A π=.选②.由cos 2cos cos c A b A a C =-及正弦定理得sin cos 2sin cos sin cos C A B A A C =-, ∴()2sin cos sin cos sin cos sin sin B A C A A C A C B =+=+=, 由于△ABC 中,sin 0B ≠,()0,A π∈, ∴2cos 1A =,即1cos 2A =, ∴3A π=.选③. 由cos cos 2cos cos b C c Ba A A -=及正弦定理得sin cos sin cos 2sin cos cos B C C B A A A-=, ∴2sin cos sin cos sin cos A A B C C B -=,∴()2sin cos sin cos sin cos sin sin A A C B B C B C A =+=+=, 由于△ABC 中,()0,A π∈,sin 0A ≠, ∴2cos 1A =,即1cos 2A =, ∴3A π=.(2)由将3A π=,1a =代入余弦定理2222cos a b c bc A =+-得221b c bc =+-,∴()213b c bc +=+,即2()13b c bc +-=,由于2b c +()24b c bc +≤, ∴()()22134b c b c +-+≤,解得2b c +≤,(当且仅当1b c ==时取等)又1b c a +>=,∴12b c <+≤,即23a b c <++≤, ∴求△ABC 的周长的取值范围是(]2,3.17.在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,S 为ABC 的面积,且()222S a b c =-- (1)求sin A ,cos A 的值(2)求2b c的取值范围 【答案】(1)4sin 5A =;3cos 5A =;(2)35,106⎛⎫ ⎪⎝⎭. (1)∵()222S a b c =--,1sin 2S bc A = ∴()22sin bc A a b c =--, ∴2222sin 2cos b c a A A bc+-=-=, ∴1cos 1sin 2A A =-, 又∵22sin cos 1A A +=, ∴221sin 1sin 12A A ⎛⎫+-= ⎪⎝⎭ ∴5sin sin 104A A ⎛⎫-= ⎪⎝⎭, ∴sin 0A =(舍),4sin 5A =, 又∵ABC 为锐角三角形,∴3cos 5A =. (2)∵πA B C ++=,∴()sin sin B A C =+, ∴sin sin cos cos sin 22sin 2sin b B A C A C c C C+== 432cos sin 35552sin tan 10C C C C +==+ ∵ABC 为锐角三角形,∴90C <︒,90A C +>︒,∴90C A >︒-,()cos 3tan tan 90sin 4A C A A >︒-==, ∴140tan 3C <<,2850tan 15C <<, ∴35,2106b c ⎛⎫∈ ⎪⎝⎭. 18.在△ABC 中,a ,b ,c 分别为A ,B ,C 所对边,sin sin tan cos cos A B C A B+=+.(1)求cos C 的值;(2)若sin A =,求b c 的值.【答案】(1)12(2)21 (1)由sin sin tan cos cos A B C A B+=+,可得sin sin sin cos cos cos C A B C A B +=+ 则()()sin cos cos cos sin sin C A B C A B +=+, 由正弦定理得()()cos cos cos c A B a b C +=+ 由余弦定理得()222222222222b c a a c b a b c c a b bc ac ab ⎛⎫+-+-+-+=+ ⎪⎝⎭整理得()()2220a b a b c ab ++--=,又0a b +>,则2220a b c ab +--= 则2221cos 222a b c ab C ab ab +-===, (2)由(1)可知1cos 2C =,又0πC <<,则π3C =,由sin 1A =≠,可知角A 为钝角或锐角若A 为钝角,则2π2πsin sin ,π33A A A C =<=⇒>∴+> 这与ABC 内角和为π矛盾,即A 不能为钝角,A ∴为锐角,由sin A =,可得cos A =()1sin sin sin cos cos sin 2B A C A C A C ∴=+=+==sinsin b B c C ∴==。
六年级数学上册典型例题系列之第五单元圆的周长问题基础部分(解析版)编者的话:《六年级数学上册典型例题系列》是基于教材知识点和常年考点考题总结和编辑而成的,其优点在于选题典型,考点丰富,变式多样。
本专题是第五单元圆的周长问题基础部分,后续内容为《圆的周长问题提高部分》。
本部分内容主要是以圆的周长为基础,多考察圆周长公式的实际应用及各数量关系的转化,考试也多以填空、选择、应用为主,难度较小,考题较为典型,共划分为十一个考点,欢迎使用。
【考点一】直径与半径的关系类型题。
【方法点拨】1.在同一个圆内,有无数条半径,有无数条直径。
2.在同一个圆内,直径的长度是半径的2倍,半径的长度是直径的一半。
3.用字母表示为:d=2r r=d÷2用文字表示为:半径=直径÷2 直径=半径×2【典型例题1】圆的半径是4厘米,则圆内最长的线段长是()厘米。
解析:根据直径与半径的数量关系,4×2=8(厘米)【典型例题2】看图填空。
解析:5cm;7cm【典型例题3】看图填空。
圆的直径是()厘米,正方形的边长是()厘米。
解析:6;6【对应练习1】看图填空。
半圆的半径是________dm,直径是________dm。
解析:8;16【对应练习2】看图填空。
长方形的长是________cm,宽是________cm。
解析:12;6【对应练习3】看图填空。
大圆的半径是________ cm,直径是________ cm;小圆的半径是________ cm,直径是________ cm;解析:10;20;5;10【考点二】长方形内圆的数量问题。
【方法点拨】以固定直径在长方形内画圆,只能画整圆,因此需要计算出长、宽两边各能画多少个圆,再将数量相乘。
【典型例题】用一块长1米,宽0.8米的长方形铁皮,做一种直径是4分米的圆形交通标志牌,怎样取材比较合理?最多能做多少个交通标志牌?解析:长边:10÷4≈2(个)宽边:8÷4=2(个)一共:2×2=4(个)答:略。
求篱笆周长的应用题引言篱笆是用来围起农田或者花园的一种常见设施,其周长的计算对于农民和园艺爱好者来说非常重要。
在这篇文章中,我们将介绍一个应用题,探讨如何计算篱笆的周长,并通过实例解决相关问题。
问题描述我们的问题是计算一个矩形花园的篱笆周长。
假设我们有一个矩形花园,其长度为10米,宽度为5米。
我们需要计算围绕该花园的篱笆的周长。
解决方法我们可以通过两个步骤来解决这个问题:计算矩形的周长,再添加上门的长度。
步骤一:计算矩形的周长矩形的周长等于将长度和宽度相加的两倍。
根据我们的问题描述,矩形的长度为10米,宽度为5米。
因此,矩形的周长可以通过以下方式计算:周长$ = 2 (长度 + 宽度)$ 周长$ = 2 (10 + 5)$ 周长$ = 30$米因此,矩形的周长为30米。
步骤二:添加上门的长度在我们的问题描述中没有提及门的长度,因此我们需要添加上门的长度来获取完整的篱笆周长。
假设我们的花园有一扇门,门的宽度为1米。
因此,我们需要将门的宽度添加到矩形的周长中。
篱笆周长$ = 矩形的周长 + 门的宽度$ 篱笆周长$ = 30 + 1$ 篱笆周长$ = 31$米因此,矩形花园的篱笆周长为31米。
实例应用现在,让我们通过一个实例来应用我们所学的知识。
实例描述假设我们有一个长方形花园,其长度为12米,宽度为8米。
我们需要计算围绕该花园的篱笆的周长。
步骤一:计算矩形的周长根据实例描述,矩形的长度为12米,宽度为8米。
我们可以使用之前提到的公式来计算矩形的周长:周长$ = 2 (12 + 8)$ 周长$ = 40$米因此,矩形的周长为40米。
步骤二:添加上门的长度在这个实例中也没有提到门的长度,我们假设门的宽度为0.5米。
使用之前的公式,我们可以计算篱笆的周长:篱笆周长$ = 40 + 0.5$ 篱笆周长$ = 40.5$米因此,长方形花园的篱笆周长为40.5米。
总结通过以上的例子,我们可以看出计算篱笆周长的求解步骤。
第五单元 美化校园——图形的周长【例1】下图是一个楼梯的侧面图。
已知每步台阶宽3分米,高2分米。
你能算出这个楼梯侧面的周长是多少分米吗?思路分析:此题考查点是不规则图形的周长的求法,实际还是考查长方形的周长的计算方法。
可以把原图变化一下,转化成一个长方形。
可以把每层台阶的宽度向上平移到和最上层台阶同样高的地方,把每层台阶的高度再向右平移到台阶的最右侧,这样原图就转化成一个长方形,原图和现在的长方形的周长是一样的,原楼梯侧面的周长就可以求出来了。
解答:(3×6+2×6)×2=60(分米)答:这个楼梯侧面的周长是60分米。
【例2】把一个边长是10厘米的正方形剪成4个完全相同的小正方形,这个4个小正方形的周长和比原来正方形的周长增加了多少厘米?思路分析:解决此题的关键是知道如何根据题意来剪开正方形,在由大正方形剪成小正方形的过程中,正方形的边长数量有怎样的变化。
根据题意可以如下图所示,把这个大正方形剪成小正方形。
即把正方形沿中线竖直方向剪一刀,周长和就比原来正方形的周长增加2个边长,再把正方形沿中线水平方向剪一刀,周长和又增加了2个边长,一共增加了2×2=4(个)边长,所以这4个小正方形的周长和比原来大正方形的周长增加了10×4=40(厘米)。
解答:10×(2×2)=40(厘米)。
答:这个4个小正方形的周长和比原来正方形的周长增加了40厘米。
【例3】一块长方形花圃,长8米、宽6米。
它的一边靠墙,其余3边围上篱笆,篱笆至少要多少米?思路分析:本题考查的知识点是利用分类讨论的方法解答“篱笆靠墙”问题。
解答时可以用分类讨论的方法,画出图形(如下图):假设长和宽分别做墙壁时,求出需要的篱笆的米数。
解答:长做墙:8+6×2=20(米)宽做墙:6+8×2=22(米)答:需要篱笆的长是20米或22米。
【例4】一块长方形的玻璃的周长是24厘米,把3块这样的长方形玻璃恰好可以拼成一块正方形的玻璃(如图),正方形玻璃的周长是多少厘米?思路分析:此题的考查点实际是长方形和正方形的周长的计算方法。
与圆周长相关的问题1. 圆周长的定义和计算公式圆周长是指圆形的边界长度,也可以称为圆形的周长。
圆周长的计算公式是:C = 2πr其中,C表示圆周长,π是一个常数,近似取值为3.,r表示圆的半径。
2. 圆周长与半径的关系从圆周长的计算公式可以看出,圆周长与圆的半径是正相关的。
即,半径增加,圆周长也会增加;半径减小,圆周长也会减小。
3. 圆周长的单位圆周长的单位是长度单位,通常使用米、厘米、毫米等进行表示。
具体使用哪种单位取决于具体场景和需求。
4. 圆周长的应用圆周长在日常生活和各种应用中都有广泛的应用。
以下是一些与圆周长相关的问题和应用实例:- 紧围绕圆形花坛的铁丝网需要多长?- 一根有弹性的绳子,如果将其围绕一个圆形物体,绳子的长度需要多长?- 一个圆形跑道的周长是多少?若要将圆形跑道铺设橡胶跑道,需要多少材料?通过计算圆周长,我们可以得到准确的长度数据,进而进行设计、规划以及材料采购等工作。
5. 圆周长的计算实例下面是两个以具体数值计算圆周长的实例:实例一:若一个圆的半径为5厘米,计算其周长。
解:根据圆周长的计算公式可知:C = 2πr代入已知的半径值:C = 2 * 3. * 5 = 31.4159厘米所以,该圆的周长为31.4159厘米。
实例二:若一个圆的半径为3米,计算其周长。
解:根据圆周长的计算公式可知:C = 2πr代入已知的半径值:C = 2 * 3. * 3 = 18.米所以,该圆的周长为18.米。
总结通过以上介绍可知,圆周长是与圆的半径密切相关的,可以通过圆周长的计算公式进行准确计算。
圆周长在生活和工作中有着广泛的应用,如设计、规划和材料采购等。
了解和掌握圆周长的计算方法对于解决与圆形相关的问题非常重要。
面积经典问题
【经典例题1】用15米长的木栏沿着围墙围一个种花草的长方形或者正方形的苗圃,其中一面利用围墙,如果每边的长度都是整数,那么有几种围法,怎样围才能使围成的面积最大?
【经典例题2】一个正方形的花坛,四周有1米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?
【经典例题3】一张长方形纸片,在长边上剪下5厘米,宽边上剪下2厘米,余下的部分正好是一个正方形,已知正方形的面积比原来长方形面积少66平方厘米,求正方形面积。
【经典例题4】一块正方形的玻璃,一边截去12厘米,另一边截去8厘米,剩下的长方形面积比原来的正方形减少1764平方厘米,原正方形玻璃的边长是多少厘米?
【经典例题5】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个,第四个,第五个正方形,求第五个正方形的面积。
【经典例题6】如图,是一个楼梯的截面图,高280厘米,每阶台阶的宽和高都是20厘米,这楼梯的截面积是多少平方厘米?
【答案】
【经典例题1】用15米长的木兰沿着围墙围一个种花草的。
解三角形专题练:周长最值与范围问题(含答案解析)求周长的最值或取值范围的问题,通常有两种途径,其一是运用余弦定理结合基本不等式求解,其二是运用正弦定理、辅助角公式结合三角函数求解.一、知识点1.基本不等式:ab b a 2≥+;2.正弦定理:Cc B b A a sin sin sin ==,余弦定理:A bc c b a cos 2222-+=等;3.和差公式:()βαβαβα±=±sin sin cos cos sin ;()βαβαβα cos cos cos cos cos =±4.二倍角公式:αααcos sin 22sin =,ααα22sin cos 2cos -=,ααα2tan 1tan 22tan -=.5.辅助角公式:),sin(cos sin )(22ϕ++=+=x b a x b x a x f (其中ab =ϕtan ).二、典型例题【例1】:△ABC 的内角A,B,C 的对边分别为a,b,c 且满足a=2,cos (2)cos a B c b A =-.(1)求角A 的大小;(2)求△ABC 周长的范围.【解析】:(1)解法一:由已知,得cos cos 2cos a B b A c A +=.由正弦定理,得sin cos sin cos 2sin cos A B B A C A +=.即sin()2sin cos A B C A +=,因为sin()sin A B C +=.所以sin 2sin cos C C A =.因为sin 0C ≠,所以1cos 2A =,因为0A π<<,所以3A π=.解法二:结合余弦定理222222(2)22a c b b c a a c b ac bc +-+-⨯=-⨯,即222b c a bc +-=.所以2221cos 22b c a A bc +-==.因为0A π<<,所以3A π=.(2)解法一:由余弦定理2222cos a b c bc A =+-,得224bc b c +=+,即2()34b c bc +=+.因为22⎪⎭⎫⎝⎛+≤c b bc ,所以()()44322++≤+c b c b .即4≤+c b (当且仅当2b c ==时等号成立).又因为a c b >+,所以64≤++<c b a .解法二:sin sin sin a b c A B C ==,且2a =,3A π=,所以43sin 3b B =,433c C =,所以22sin )2[sin sin()]24sin()3336a b c B C B B B ππ++=++=++-=++,因为203B π<<,所以64≤++<c b a ,【例2】:已知a,b,c 分别为△ABC 三个内角A,B,C 的对边,cos sin 0a C C b c +--=.(1)求A 的大小;(2)若a =7,求△ABC 的周长的取值范围.【解析】:(1)由已知及正弦定理得:C B C A C A sin sin sin sin 3cos sin +=+,即C C A C A C A sin )sin(sin sin 3cos sin ++=-,化简得1cos sin 3=-A A ,所以21)6sin(=-πA ,所以66ππ=-A ,解得3π=A ;(2)由已知:0b >,0c >,7b c a +>=,由余弦定理()()()()222222414333cos249c b c b c b bc c b bc c b +=+-+≥-+=-+=π,当且仅当b =c =7时等号成立,所以2()449b c +≤⨯,又因为b +c >a,所以7<b +c ≤14,从而△ABC 的周长的取值范围是(14,21].三、巩固练习1.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c,且2sin (2)sin (2)sin a A b c B c b C =+++.(Ⅰ)求角A ;(Ⅱ)若a=2,求△ABC 周长的取值范围.2.已知△ABC 中,角A,B,C 所对的边分别为a,b,c ,且满足sin (sin )A B B C +=.(1)求角A 的大小;(2)若a=3,求△ABC 周长的取值范围.3.锐角△ABC 中,角A,B,C 所对的边分别为a,b,c ,且(cos )0c a B B -+=.(1)求角A 的大小;(2)若a =ABC 周长的取值范围.4.在△ABC 中,角A,B,C 的对边分别为a,b,c ,b=4,()sin ()(sin sin )a c A b c B C -=-+.(1)求角B ;(2)求△ABC 周长的最大值.5.在△ABC 中,角A,B,C 的对边分别为a,b,c ,且2,3==a A π.(1)求△ABC 的周长的取值范围;(2)求22c b +的取值范围.6.如图,在四边形ABCD 中,CD =BC =,7cos14CBD ∠=-.(1)求BDC ∠;(2)若3A π∠=,求△ABD 周长的最大值.7.(2020·理2)ABC 中,sin 2A -sin 2B -sin 2C =sin B sin C.(1)求A ;(2)若BC =3,求ABC 周长的最大值.8.已知a ,b ,c 分别为锐角△ABC 的三个内角A ,B ,C 的对边,若a =2,且)sin (sin sin 2sin C A A B +=,求△ABC 的周长的取值范围.9.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,已知向量(2cos ,)m C b =- ,(1,cos cos )n a C c A =+,且//m n.(1)求角C 的大小;(2)若c =,求ABC ∆的周长的取值范围.10.在△ABC 中,角A,B,C 的对边分别为a,b,c ,请在①(2)cos cos 0a c B b A ++=;②22cos cos sin (sin sin )A B C C A -=+中选择一个作为已知条件,解答下列问题.我选择__________.(1)求角B 的大小;(2)若3b =,求△ABC 周长的取值范围.11.在△ABC 中,角A 、B 、C 所对的边分别为c b a 、、,且满足A b B a cos 3sin =.(1)求角A 的大小;(2)若4=a ,求△ABC 周长的最大值.12.已知在△ABC 2)12sin2C A B +=+.(1)求角C 的大小;(2)若BAC ∠与ABC ∠的内角平分线交于点Ⅰ,△ABC 的外接圆半径为2,求△ABI 周长的最大值.13.(2021•上海浦东新区三模)已知函数f (x )=A sin (ωx +φ)(ω>0,20πϕ<<)的部分图象如图所示.(1)求函数f (x )的解析式;(2)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若22=⎪⎭⎫⎝⎛A f ,a =2,求△ABC 周长的取值范围.四、答案与解析1.【解析】:(1)由正弦定理sin sin sin a b cA B C ==,由2sin (2)sin (2)sin a A b c B c b C =+++⇒22(2)(2)a b c b c b c =+++,整理得222a b c bc =++,即bc a c b -=-+222,所以2122cos 222-=-=-+=bc bc bc a c b A ,因为1800<<A ,所以120=A ;(2)由正弦定理得334sin sin ==C c B b ,所以[])60sin(sin 334)sin (sin 334B B C B c b -+=+=+ )sin 60cos cos 60sin (sin 334B B B-+=)60sin(334cos 23sin 21334 +=⎪⎪⎭⎫ ⎝⎛+=B B B ,因为120=A ,所以()60,0∈B ⇒()120,6060∈+B ,⇒⎥⎦⎤⎝⎛∈+1,23)60sin(B ⇒⎦⎤ ⎝⎛∈+334,2)60sin(334B ,即⎥⎦⎤ ⎝⎛∈+334,2c b ,所以周长⎥⎦⎤⎝⎛+∈++3342,4c b a .2.【解析】:(1)由A B C π++=,得sin sin()C A B =+,代入已知条件得:sin sin cos cos sin A B A B A B A B +=⇒sin sin sin A B A B =,因为0sin ≠B,由此得tan A =,因为π<<A 0,所以3π=A .(2)由上可知:23B C π+=,所以B C -=32π.由正弦定理得:32sin sin 3a R A π===所以232(sin sin )sin()]sin )6sin()326b c R B C B B B B B ππ+=+=+-=+=+,因为由203B π<<得:16sin 21≤⎪⎭⎫ ⎝⎛+<πB ,所以63≤+<c b ,且3a =,故△ABC 周长的取值范围为(6,9].3.【解析】:(1)因为锐角△ABC 中(cos )0c a B B -+=,所以由正弦定理可得sin sin (cos )0C A B B -+=,所以sin sin cos sin C A B A B ∴-=,所以sin()sin cos sin A B A B A B ∴+-=,所以3sin cos sin cos sin cos sin sin 3A B A B A B A B ∴+-=,即3sin cos sin 3A B A B =,约掉sin A 变形可得sin tan cos B B B ==,3A π=;(2)因为3=a ,3A π=,所以32π=+C B ,所以由正弦定理可得sin 2sin sin a B b B A ==,sin 2sin sin a Cc C A==,所以△ABC 周长为2sin 2sin a b c B C ++=++22sin 2sin()3B B π=++-312sin 2(sin )22B B B =++2sin sin B B B =+3sin B B =+1cos )22B B =+)6B π=++,因为320π<<B ⇒5666B πππ<+<⇒16sin 21≤⎪⎭⎫ ⎝⎛+<πB ⇒326sin 323≤⎪⎭⎫ ⎝⎛+<πB ,所以336sin 32332≤⎪⎭⎫ ⎝⎛++<πB ,所以△ABC 周长的取值范围为.4.【解析】:(1)由正弦定理知,sin sin sin a b cA B C==,因为()()()C B c b A c a sin sin sin +-=-,所以()()()c b c b a c a +-=-,整理得222a c b ac +-=,由余弦定理知,2221cos 222a cb ac B ac ac +-===,因为()π,0∈B ,所以3π=B .(2)由(1)知,3B π=,所以32π=+C A ,由正弦定理知,4sin sin sin sin 3a cb A C B π====A a sin 38=,c C =,所以()⎪⎪⎭⎫ ⎝⎛++=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=+=+A A A A A C A c a sin 21cos 23sin 3832sin sin 38sin sin 38π3(sin ))8sin(266A A A A ππ=+=+=+,因为⎪⎭⎫ ⎝⎛∈32,0πA ,所以⎪⎭⎫ ⎝⎛∈+65,66πππA ,当62A ππ+=,即3A π=时,a c +取得最大值8,所以1248=+≤++c b a ,故△ABC 周长的最大值为12.5.【解析】:(1)由正弦定理得,k A a C c B b =====334232sin sin sin ,易得:C B C k c B k b -===π32,sin ,sin ,所以⎪⎭⎫ ⎝⎛+=+=+6sin 4)sin (sin πC C B k c b 由⎪⎭⎫ ⎝⎛∈π32,0C ,得⎪⎭⎫⎝⎛∈+65,66πππC ,则有:]4,2(∈+c b 又2=a ,则].6,4(∈++=∆c b a l ABC (2)()⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛+-=+=+)62sin(211sin )32(sin sin sin 222222222ππC k C C k C B k c b 由⎪⎭⎫ ⎝⎛∈π32,0C ,得⎪⎭⎫ ⎝⎛-∈-67,662πππC ,则]21,41(62sin 21-∈⎪⎭⎫ ⎝⎛-πC ,所以23,43(62sin 211∈⎪⎭⎫ ⎝⎛-+πC 又3162=k ,则].8,4(22∈+c b 6.【解析】:(1)在BCD ∆中,7cos 14CBD ∠=-,所以321sin 14CBD ∠===,由正弦定理得sin sin CD BCCBD BDC=∠∠,所以321sin 114sin 2BC CBD BDC CD ⋅∠∠===,又因为CBD ∠为钝角,所以BDC ∠为锐角,故6BDC π∠=;(2)在BCD ∆中,由余弦定理得2222cos214BC BD CD CBD BC BD +-∠===-⋅,解得4BD =或5BD =-(舍去),在△ABD 中,3A π∠=,设AB x =,AD y =,由余弦定理得22222161cos 222AB AD BD x y A AB AD xy +-+-===⋅⇒2216x y xy +-=⇒2()163x y xy +-=,又0x >,0y >,利用基本不等式得()()4331622y x xy y x +≤=-+,即()642≤+y x ,当且仅当4x y ==时,等号成立,所以x y +的最大值为8,所以AB AD BD ++的最大值为8412+=,所以△ABD 周长的最大值为12.7.【解析】:(1)由正弦定理可得:222BC AC AB AC AB --=⋅,所以2221cos 22AC AB BC A AC AB +-∴==-⋅,因为()0,A π∈ ,所以23A π∴=.(2)由余弦定理得:222222cos 9BC AC AB AC AB A AC AB AC AB =+-⋅=++⋅=,即()29AC AB AC AB +-⋅=.因为22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭(当且仅当AC AB =时取等号),所以()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭,解得:AC AB +≤(当且仅当AC AB =时取等号),所以△ABC 周长3L AC AB BC =++≤+ABC 周长的最大值为3+.8.【解析】:因为a =2,且)sin (sin sin 2sin C A A B +=,所以由正弦定理可得b 2=a 2+ac ,由余弦定理可得bac bc ac c bc a b c A 222cos 2222+=+=-+=,同理可得:b ac B 2cos -=,即⎩⎨⎧=-=+Ba a c Ab ac cos 2cos 2,消去c ,可得B a A b a cos 2cos 22-=,由正弦定理可得B A A B A cos sin 2cos sin 2sin 2-=,即)sin(2sin 2A B A -=,可得B =2A ,由正弦定理B b A a sin sin =,可得AbA 2sin sin 2=,可得A b cos 4=,因为△ABC 为锐角三角形,且π=++C B A ,所以220π<<A ⇒46ππ<<A ⇒23cos 22<<A ⇒3222<<b .又因为a =2,即b 2=4+2c ,所以△ABC 的周长为b b b b c b a +=-++=++2221242,由二次函数性质可得,△ABC 的周长的取值范围为:(326,224++).9.【解析】:(1)由//m n得22cos 2cos cos a C c A C b +=-,由正弦定理sin sin sin a b cA B C==,得2cos (sin cos sin cos )sin C A C C A B +=-,即2cos sin()sin C A C B +=-,因为在三角形中sin()sin 0A C B +=≠,则1cos 2C =-,又(0,)C π∠∈,故23C π∠=;(2)解法一:在△ABC 中,因为c =,23C π∠=,由余弦定理得2223c a b ab =++=,即22()332a b a b ab +⎛⎫+=+≤+ ⎪⎝⎭,当且仅当a b =时取等号,解得2a b +≤,又由三角形性质得a b c +>=2a b <+≤,则2a b c <++≤+,即ABC ∆的周长的取值范围为(.解法二:由正弦定理知:2233sin sin sin ====CcB b A a ,则A a sin 2=,B b sin 2=3sin 2sin 2++=∆B A l ABC 332sin 2sin 23)sin(2sin 2+⎪⎭⎫ ⎝⎛++=+++=πA A C A A 33sin 23cos 3sin +⎪⎭⎫ ⎝⎛+=++=πA A A 因为0,3A π⎛⎫∈ ⎪⎝⎭,则2,333A πππ⎛⎫+∈ ⎪⎝⎭,故sin ,132A π⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭因此()32,32+=∆ABC l .10.【解析】:(1)若选①,已知(2)cos cos 0a c B b A ++=.则:(sin 2sin )cos sin cos 0A C B B A ++=,整理得:sin cos cos sin 2sin cos 0A B A B C B ++=,解得:1cos 2B =-,又0B π<<,所以23B π=.若选②,因为()A C C B A sin sin sin cos cos 22+=-.所以()C A C B A sin sin sin sin 1sin 1222+=---,所以C A B C A sin sin sin sin sin 222-=-+,所以ac b c a -=-+222,所以212cos 222-=-+=ac b c a B ,又0B π<<,所以32π=B .(2)解法一:因为23B π=,3b =,所以由余弦定理知,()()()2222222432cos 29c a c a c a ac c a B ac c a b +=⎪⎭⎫ ⎝⎛+-+≥-+=-+==,当且仅当3==c a 时,等号成立,所以32≤+c a ,又因为b c a >+,所以3326+≤++<c b a .解法二:因为sin sin sin a b c A B C ===,所以A a sin 32=,c C =,则△ABC 的周长()33sin sin 323sin sin 32+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=++=++=A A C A c b a lπ1sin )32A A A =+-+)33A π=++,因为30π<<A ,2333A πππ<+<,所以13sin 23≤⎪⎭⎫ ⎝⎛+<πA ,即33233sin 326+≤+⎪⎭⎫ ⎝⎛+<πA ,所以△ABC 周长的取值范围是(6,3]+.11.【解析】:(1)依正弦定理Bb A a sin sin =可将A b B a cos 3sin =化为A B B A cos sin 3sin sin =又因为在△ABC 中,0sin >B ,所以A A cos 3sin =,即3tan =A ,因为π<<A 0,所以3π=A .(2)因为△ABC 的周长c b c b a ++=++=4,所以当c b +最大时,△ABC 的周长最大.解法一:因为bc c b A bc c b a 3)(cos 2162222-+=-+==,所以316)(2-+=c b bc 4)(2c b bc +≤且,所以()()431622c b c b +≤-+,所以()642≤+c b ,所以8≤+c b (当且仅当4==c b 时等号成立)所以△ABC 周长的最大值12.解法二:因为sin sin sin 332a b c A B C ====,所以()83832sin sin sin sin 8sin 3336b c B C B B B ππ⎡⎤⎛⎫⎛⎫+=+=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,20,3B π⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭故当且仅当3B π=时,b c +取到最大值8所以△ABC 周长的最大值1212.【解析】:(1)因为2)12sin 2C A B +=+,且A B C π++=,11cos 2cos C C C =+-=-cos 2C C +=⇒26sin 2=⎪⎭⎫ ⎝⎛+πC .因为()π,0∈C ⇒⎪⎭⎫ ⎝⎛∈+67,66πππC ⇒26ππ=+C ,即3C π=.(2)因为△ABC 的外接圆半径为2,所以由正弦定理知,4223sin sin =⨯==∠πAB ACB AB ,所以32=AB ,因为3π=∠ACB ,所以32π=∠+∠BAC ABC ,因为BAC ∠与ABC ∠的内角平分线交于点Ⅰ,所以3π=∠+∠BAI ABI ,所以32π=∠ABI ,设ABI θ∠=,则3BAI πθ∠=-,且03πθ<<,在△ABI中,由正弦定理得,42sin sin sin()sin 33BI AI AB AIB ππθθ====∠-,所以⎪⎭⎫ ⎝⎛-=θπ3sin 4BI ,θsin 4=AI ,所以△ABI的周长为314sin()4sin 4(cos sin )4sin 322πθθθθθ+-+=-+2sin 4sin(3πθθθ=+=++,因为30πθ<<,所以2333πππθ<+<,所以当32ππθ+=,即6πθ=时,△ABI的周长取得最大值为4+,故△ABI的周长的最大值为4+.13.【解析】:(1)根据函数的图象,函数的周期πππ=⎪⎭⎫ ⎝⎛-⨯=12512112T ,故ω=2.由于点⎪⎭⎫ ⎝⎛0,125π满足函数的图象,所以01252sin =⎪⎭⎫ ⎝⎛+⨯ϕπA ,由于20πϕ<<,所以6πϕ=.由于点(0,1)在函数的图象上,所以A =2.故函数⎪⎭⎫ ⎝⎛+=62sin 2)(πx x f .(2)由于26sin 2)2(=⎪⎭⎫ ⎝⎛+=πA A f ,所以3π=A .由正弦定理:34sin sin ==A a B b ,整理得B b sin 34=,同理⎪⎭⎫ ⎝⎛-==B C c 32sin 34sin 34π,由于⎪⎭⎫ ⎝⎛∈32,0πB ,所以⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛-++=++=∆6sin 4232sin 34sin 342ππB B B c b a l ABC ,由于⎪⎭⎫ ⎝⎛∈32,0πB ⇒⎪⎭⎫ ⎝⎛∈+65,66πππB ⇒⎥⎦⎤ ⎝⎛∈⎪⎭⎫ ⎝⎛+1,216sin πB .所以:l △ABC ∈(4,6].。