当前位置：文档之家 › K-means聚类分析

K-means聚类分析

  • 格式：pdf
  • 大小：205.82 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

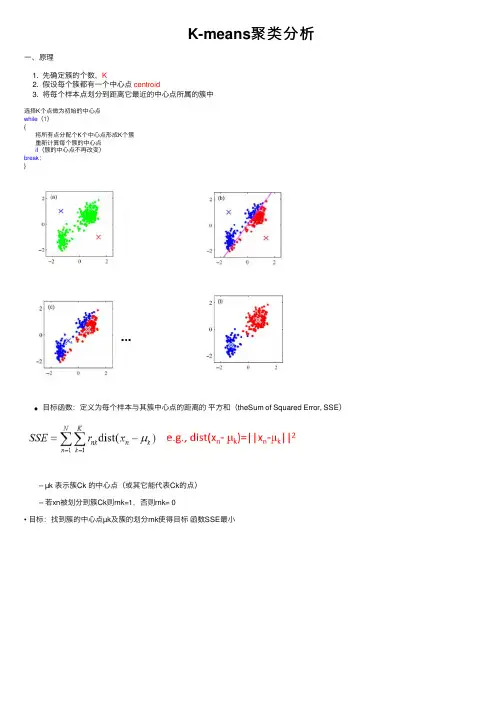
K-means聚类分析

K-means聚类分析

K-means聚类分析⼀、原理1. 先确定簇的个数，K2. 假设每个簇都有⼀个中⼼点centroid3. 将每个样本点划分到距离它最近的中⼼点所属的簇中选择K个点做为初始的中⼼点while（1）{将所有点分配个K个中⼼点形成K个簇重新计算每个簇的中⼼点if（簇的中⼼点不再改变）break；}⽬标函数：定义为每个样本与其簇中⼼点的距离的平⽅和（theSum of Squared Error, SSE） – µk 表⽰簇Ck 的中⼼点（或其它能代表Ck的点） – 若xn被划分到簇Ck则rnk=1，否则rnk= 0• ⽬标：找到簇的中⼼点µk及簇的划分rnk使得⽬标函数SSE最⼩初始中⼼点通常是随机选取的（收敛后得到的是局部最优解）不同的中⼼点会对聚类结果产⽣不同的影响：1、2、此时你⼀定会有疑问：如何选取"较好的"初始中⼼点？1. 凭经验选取代表点2. 将全部数据随机分成c类，计算每类重⼼座位初始点3. ⽤“密度”法选择代表点4. 将样本随机排序后使⽤前c个点作为代表点5. 从(c-1)聚类划分问题的解中产⽣c聚类划分问题的代表点 结论：若对数据不够了解，可以直接选择2和4⽅法需要预先确定K Q：如何选取K SSE⼀般随着K的增⼤⽽减⼩A：emmm你多尝试⼏次吧，看看哪个合适。

斜率改变最⼤的点⽐如k=2总结：简单的来说，K-means就是假设有K个簇，然后通过上⾯找初始点的⽅法，找到K个初始点，将所有的数据分为K个簇，然后⼀直迭代，在所有的簇⾥⾯找到找到簇的中⼼点µk及簇的划分rnk使得⽬标函数SSE最⼩或者中⼼点不变之后，迭代完成。

成功把数据分为K类。

预告：下⼀篇博⽂讲K-means代码实现。

k-means聚类和fcm聚类的原理概念

k-means聚类和fcm聚类的原理概念

k-means聚类和fcm聚类的原理概念摘要：一、聚类分析概述1.定义与作用2.常用的聚类算法二、K-means 聚类原理1.算法基本思想2.计算过程3.特点与优缺点三、FCM 聚类原理1.算法基本思想2.计算过程3.特点与优缺点四、K-means 与FCM 聚类的比较1.相似之处2.不同之处3.适用场景正文：一、聚类分析概述聚类分析是一种无监督学习方法，通过将相似的数据对象归为一类，从而挖掘数据集的潜在结构和模式。

聚类分析在数据挖掘、模式识别、图像处理、生物学研究等领域具有广泛应用。

常用的聚类算法有K-means 聚类和FCM 聚类等。

二、K-means 聚类原理1.算法基本思想K-means 聚类是一种基于划分的聚类方法，通过迭代计算数据点与当前中心点的距离，将数据点分配到距离最近的中心点所属的簇，然后更新中心点。

这个过程持续进行，直到满足停止条件。

2.计算过程（1）随机选择k 个数据点作为初始中心点。

（2）计算其他数据点与初始中心点的距离，将数据点分配到距离最近的簇。

（3）计算每个簇的中心点。

（4）重复步骤2 和3，直到中心点不再发生变化或达到最大迭代次数。

3.特点与优缺点特点：简单、易于实现，适用于大规模数据集。

优点：可以处理大规模数据集，对噪声数据具有一定的鲁棒性。

缺点：对初始中心点敏感，可能导致局部最优解；计算过程中需要反复计算距离，计算量较大。

三、FCM 聚类原理1.算法基本思想FCM 聚类是一种基于模糊划分的聚类方法，通过计算数据点与当前中心点的模糊距离，将数据点分配到距离最近的簇。

模糊距离是基于隶属度函数计算的，可以反映数据点对簇的隶属程度。

2.计算过程（1）随机选择k 个数据点作为初始中心点。

（2）计算其他数据点与初始中心点的模糊距离，将数据点分配到距离最近的簇。

（3）计算每个簇的中心点。

（4）重复步骤2 和3，直到中心点不再发生变化或达到最大迭代次数。

3.特点与优缺点特点：考虑了数据点对簇的隶属程度，具有更好的全局优化性能。

Python中的聚类分析方法和应用

Python中的聚类分析方法和应用

Python中的聚类分析方法和应用聚类分析是一种数据挖掘技术，在数据分析、机器学习、人工智能等领域都有广泛的应用。

它的基本思想是将相似的样本归为同一类，不同的样本归为不同的类，从而实现对数据的分类和整理。

Python作为一种强大的编程语言，也提供了多种聚类分析算法的实现，以下是聚类分析在Python中的应用及其方法。

一、K-Means算法K-Means算法是一种经典的聚类算法，常用于分析数量较大的数据集。

K-Means算法通过不断迭代的方式，将数据集中的每一个样本归为k个簇中的某一个。

它的基本流程如下：首先从数据集中随机选取k个样本作为簇的中心点，然后计算数据集中其他样本与这k个簇中心点的距离，并将距离最近的样本分配给它所对应的簇。

接着重新计算每个簇的中心点，并重复这个过程，直到目标函数收敛或达到指定的迭代次数。

在Python中，K-Means算法的实现非常简单，主要依托于scikit-learn库。

引入sklearn.cluster包，并使用KMeans类即可。

以下是一个简单的Python代码示例：```from sklearn.cluster import KMeansimport numpy as npdata = np.random.rand(1000, 2)kmeans = KMeans(n_clusters=3, random_state=0).fit(data) labels = bels_centers = kmeans.cluster_centers_```其中，随机生成1000个二维数据作为数据集，然后使用KMeans 类进行聚类，将数据集划分为3个簇。

最后，通过labels和centers 变量获取分类信息和中心点坐标。

二、层次聚类算法层次聚类算法是另一种经典的聚类算法，在Python中同样得到了广泛的应用。

层次聚类算法又被称为自底向上聚类（bottom-up clustering）或自上而下聚类（top-down clustering），它的基本思想是不断合并距离最近的样本，直到所有的样本都被归为一类为止。

聚类算法：K-Means和DBSCAN的比较

聚类算法：K-Means和DBSCAN的比较

聚类算法：K-Means和DBSCAN的比较聚类是一种无监督学习的方法，它将数据分组成具有相似特征的集合，称为簇(cluster)。

簇分析是统计学、计算机科学、机器学习和数据挖掘等领域中的常用技术之一。

目前，聚类算法已广泛应用于用户行为分析、市场营销、图像处理、生物信息学、搜索引擎、社交网络等领域。

在聚类算法中，K-Means和DBSCAN是两种具有代表性的算法。

本文将从算法原理、优缺点、适用场景等方面对它们进行比较分析。

一、K-Means算法K-Means算法是一种基于距离的聚类算法。

它的基本思想是从数据集中选取k个初始聚类中心，不断迭代，把每个数据点归为距离最近的聚类中心所在的簇。

K-Means算法的优点是计算简单、速度快、可并行计算，适用于处理大规模数据集。

但是K-Means算法的聚类结果受初始聚类中心的影响较大，算法的性能对于簇的形状、大小和分布较为敏感。

算法流程：1.选择k个聚类中心2.对于每个数据点，计算距离最近的聚类中心，将其划分到相应的簇中3.对于每个簇，重新计算该簇的聚类中心4.重复步骤2和步骤3，直到聚类中心不再变化或达到最大迭代次数二、DBSCAN算法DBSCAN算法是一种基于密度的聚类算法。

它的基本思想是将密度高于某一阈值的数据点定义为核心点(Core Points)，将与核心点距离不超过一定距离的数据点归为同一个簇(Cluster)，将距离较远的数据点称为噪声点(Noise)。

DBSCAN算法的优点是可以自动识别任意形状的簇，对初始聚类中心不敏感，适用于处理稠密数据集。

但是DBSCAN算法的聚类结果对于数据点密度分布的敏感度较高，平均时间复杂度较高。

算法流程：1.对于每个数据点，计算其邻域(Neighborhood)内的数据点个数，如果邻域内的数据点个数大于等于密度阈值，则该点为核心点，否则该点为噪声点2.将所有核心点加入到一个簇中，对每个核心点进行扩展，将邻域内的数据点加入到该簇中，直到不能再扩展3.继续处理下一个未被归类的核心点，直到所有核心点都在某个簇中或被标记为噪声点三、K-Means和DBSCAN的比较1.聚类精度K-Means算法适用于簇形状较为规则且大小相似的数据集，但对于不规则形状、大小差异较大的数据集，其聚类效果并不理想。

kmeans 聚类算法

kmeans 聚类算法

kmeans 聚类算法Kmeans聚类算法Kmeans聚类算法是一种基于距离的无监督机器学习算法，它可以将数据集分为多个类别。

Kmeans算法最初由J. MacQueen于1967年提出，而后由S. Lloyd和L. Forgy独立提出。

目前，Kmeans算法已经成为了机器学习领域中最常用的聚类算法之一。

Kmeans算法的基本思想是将数据集划分为k个不同的簇，每个簇具有相似的特征。

簇的数量k是由用户指定的，算法会根据数据集的特征自动将数据集分成k个簇。

Kmeans算法通过迭代的方式来更新每个簇的中心点，以此来不断优化簇的划分。

Kmeans算法的步骤Kmeans算法的步骤可以概括为以下几个步骤：1. 随机选择k个点作为中心点；2. 将每个数据点与离它最近的中心点关联，形成k个簇；3. 对于每个簇，重新计算中心点；4. 重复2-3步骤，直到簇不再变化或达到最大迭代次数。

Kmeans算法的优缺点Kmeans算法的优点包括：1. 算法简单易实现；2. 能够处理大规模数据集；3. 可以处理多维数据。

Kmeans算法的缺点包括：1. 需要用户指定簇的数量；2. 对于不规则形状的簇，效果不佳；3. 对于包含噪声的数据集，效果不佳。

Kmeans算法的应用Kmeans算法在机器学习和数据挖掘中有着广泛的应用。

以下是Kmeans算法的一些应用：1. 图像分割：将图像分为多个不同的区域；2. 文本聚类：将文本数据划分为多个主题；3. 市场分析：将消费者分为不同的群体，以便进行更好的市场分析；4. 生物学研究：将生物数据分为不同的分类。

总结Kmeans聚类算法是一种基于距离的无监督机器学习算法，它可以将数据集分为多个类别。

Kmeans算法的步骤包括随机选择中心点、形成簇、重新计算中心点等。

Kmeans算法的优缺点分别是算法简单易实现、需要用户指定簇的数量、对于不规则形状的簇效果不佳等。

Kmeans算法在图像分割、文本聚类、市场分析和生物学研究等领域有着广泛的应用。

聚类分析及k-means算法

聚类分析及k-means算法

举例应用
中国男足近几年到底在亚洲处于几流水平？下 图是采集的亚洲15只球队在2005年-2010年间大 型杯赛的战绩
对数据做了如下预处理：对于世界杯，进入决赛 圈则取其最终排名，没有进入决赛圈的，打入预 选赛十强赛赋予40，预选赛小组未出线的赋予50。 对于亚洲杯，前四名取其排名，八强赋予5，十六 强赋予9，预选赛没出现的赋予17。这样做是为了 使得所有数据变为标量，便于后续聚类。
处理后的数据如下：
数据变换：进行[0,1]规格化得到
初始类个数的选择； 初始类中心的选择；
设k=3，即将这15支球队分成三个集团。现 抽取日本、巴林和泰国的值作为三个类的种子， 即初始化三个类的中心为
A：{0.3, 0, 0.19}； B：{0.7, 0.76, 0.5}； C：{1, 1, 0.5}；
相似性度量指标
空间距离 相似系数（similarity coefficient）
空间距离
假使每个样品有p个变量，则每个样品都 可以看成p维空间中的一个点，n个样品 就是p维空间中的n个点，则第i样品与第
j 样品之间的距离记为 dij
样品距离必须满足的条件
➢ 对称性 dij d ji 0 ➢ 三角不等式 dij dik d jk ➢ dij 0 则样品i与样品j不相等
样品到类中心的距离； 归类；
计算所有球队分别对三个中心点的欧氏 距离。下面是用程序求取的结果：
第一次聚类结果： A：日本，韩国，伊朗，沙特； B：乌兹别克斯坦，巴林，朝鲜； C：中国，伊拉克，卡塔尔，阿联酋，泰
国，越南，阿曼，印尼。
重新计算类中心；
下面根据第一次聚类结果，采用k-均值法调整各个类 的中心点。
斜交空间距离
相似系数

数据聚类分析方法

数据聚类分析方法
数据聚类分析方法是一种将数据分组或分类的技术。

聚类分析的目标是将相似的数据聚集在一起，同时将不相似的数据分开。

以下是常见的数据聚类分析方法：
1. K-means聚类算法：K-means算法是一种迭代的聚类算法。

它将数据集分为预先指定的K个簇，其中每个数据点属于距离该数据点最近的簇。

该算法通过不断迭代更新簇的中心来优化聚类结果。

2. 层次聚类算法：层次聚类算法通过以下两种方法进行聚类分析：聚合和分裂。

聚合方法将每个数据点作为一个单独的簇，并逐渐将相似的簇合并在一起。

分裂方法则是从一个包含所有数据点的簇开始，并逐渐将不相似的数据点分离开来。

3. 密度聚类算法：密度聚类算法将数据点密度作为聚类的基础。

该算法通过确定数据点周围的密度来划分不同的簇。

常见的密度聚类算法有DBSCAN和OPTICS。

4. 基于网格的聚类算法：基于网格的聚类算法将数据空间划分为网格，并将数据点分配到各个网格中。

该算法通常适用于高维数据集，可以减少计算复杂度。

5. 谱聚类算法：谱聚类算法将数据点表示为一个图的拉普拉斯矩阵，并通过谱分解将数据点分配到不同的簇中。

该算法通常用于非线性可分的数据集。

需要根据具体的数据集和分析目标来选择适合的数据聚类分析方法。

K-means算法详解


算法实例
O x y
1
2 3 4 5Βιβλιοθήκη 00 1.5 5 5
2
0 0 0 2
数据对象集合S见表1，作为一个聚类分析的二 维样本，要求的簇的数量k=2。 O (1)选择 O1 0,2 ， 2 0,0 为初始的簇中心， 即 M 1 O1 0,2 ， M 2 O2 0,0 。 (2)对剩余的每个对象，根据其与各个簇中心的 距离，将它赋给最近的簇。 对 O3 ： 2 2

0 5
0 5
2

2 2
2
2
5
29
1
5
5
2



0 2

• 因为 d M 1 , O 5 d M 2 , O 5 所以将 O 5分配给 C
• 更新，得到新簇
E1 0 0
2 2
C1 O1 ,O5
和
2
C 2 O 2 , O 3 , O 4
xi1,xi2,„xid和xj1,xj2,„xjd分别是样本xi和xj对应d个描 述属性A1,A2,„Ad的具体取值。 • 样本xi和xj之间的相似度通常用它们之间的距离d(xi,xj) 来表示，距离越小，样本xi和xj越相似，差异度越小；距
离越大，样本xi和xj越不相似，差异度越大。
欧式距离公式如下：
d xi , x j
x
d k 1
ik
x jk
2
平均误差准则函数
• K-means聚类算法使用误差平方和准则函数来评价聚类 性能。给定数据集X，其中只包含描述属性，不包含类别
属性。假设X包含k个聚类子集X1,X2,„XK；各个聚类子集
中的样本数量分别为n1，n2,„,nk;各个聚类子集的均值代 表点（也称聚类中心）分别为m1，m2,„,mk。 • 误差平方和准则函数公式为：

K-means聚类分析

Cluster=GraphCluster(sim ilarityGraph)
4.1KBAC算法描述
Initialcenterset=Co mputeMinCover （simlarityGraph， aa）
record culster intinalcenter to corecanditidateset
E(Ai )
v j 1
X1, j
X2, j N
X m, j * I ( X1, j , X 2, j ,
, Xm, j )
6. I ( X1, j , X 2, j , , X m, j ) 为子集Xj的熵，计算公式为：
m
I ( X1, j , X 2, j , , X m, j ) pi, j log2 pi, j i 1
m
I (C) P(Ci ) log2 P(Ci ) i 1
P(Ci ) | Ci | / N,| Ci | 为类别Ci中样本数量，| |返回 集合中元素个数运算
4.特征属性Ai的信息增益计算公式：
Gain分成子集的熵，计算公式：
其中pi,j为Xj中的属于Ci的概率，计算公式： pi,j =|Xi,j|/Xj
7.属性Ai的信息增益比例公式为：
GainRation( Ai ) Gain( Ai ) / Spilt( Ai )
其中Spilt(Ai)计算公式：
v
Spilt( Ai ) p j * log2 Pj , 其中Pj | X j | / X j 1
每时每刻大量数据都在产生
1. 引言
目前有的聚类经典算法 1）k-means算法 2）k-原型算法 3）模糊聚类算法 4）基于粗糙的k-model算法
2. K-means聚类方法的简单分析

聚类分析方法

选方法之一 06
优缺点
缺点
对初始点的选择敏感：K-means算法的初始点选择对结果有很大影响，可能会导致不同 的初始点导致不同的聚类结果 需要预设k值：使用K-means算法需要预先设定k值，而最佳的k值可能并不容易确定
不适合大规模数据集：对于大规模数据集，K-means算法可能需要很长时间才能收敛
means||等
第1部分 算法步骤
算法步骤
以下是K-means算法的 基本步骤
算法步骤
初始化：选择k个点作为初始的聚类中心。这些点可以 是数据集中的实际数据点，也可以是随机生成的数据点
分配数据点到最近的聚类中心：对于数据集中的每个点，计 算它与k个聚类中心的距离，并将其分配到最近的聚类中心。 这一步通常使用欧氏距离来计算两点之间的距离
聚类分析—— Kmeans方法
-
目录
CONTENTS
1
算法步骤
2
优缺点
3
应用场景
2
聚类分析——Kmeans方法
聚类分析是一种无监督学习方法，用于将对象分组，使得同一组(或簇)内的对象相互之间 相似(按照某些度量方式)，而不同组之间的对象相互之间不相似。其中，K-means算法是 一种常用的聚类算法，以其发明者Arthur James和Donald Fisher的名字来命名
特征选择和降维：在聚类之前，可以 进行特征选择和降维，以减少数据的 维度和噪声，提高聚类的效果
可视化：可以将聚类结果进行可视化， 以更直观地展示聚类的效果和结果
优缺点
通过以上改进方向，可以 进一步提高K-means算法的 性能和适用性，使其在更 多的实际应用中得到广泛
应用
第3部分 应用场景
应用场景
应用场景
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
k 2
i
E 是一个数据集中所有对象的误差平方和，P 是一个对象，mi 是聚类 Ci 的质心， 即 mi
qC i
q
Ci
k‐means 聚类算法的具体步骤如下： ①从数据集中选择 k 个质心 C1，C2，…，Ck 作为初始的聚类中心； ②把每个对象分配到与之最相似的聚合。每个聚合用其中所有对象的均值来 代表， “最相似”就是指距离最小。对于每个点 Vi，找出一个质心 Cj，使它与其 间 的距离 d(Vi,Cj)最小，并把 Vi 分配到第 j 组； ③把所有的点都分配到相应的组之后重新计算每个组的质心 Cj； ④循环执行第②步和第③步，直到数据的划分不再发生变化。 该算法具有很好的可伸缩性，其计算复杂度为 O(nkt)，其中，t 是循环的次数。 K‐means 聚类算法的不足之处在于它要多次扫描数据库，此外，它只能找出球形 的 类， 而不能发现任意形状的类。 还有， 初始质心的选择对聚类结果有较大的影响， 该算法对噪声很敏感。
K‐means 聚类分析
主要的聚类算法可以分为以下几种：划分聚类、层次聚类、密度型聚类、网 格型聚类和基于模型的聚类。 划分聚类算法把数据点集分为 k 个划分，每个划分作为一个聚类。它一般从 一个初始划分开始，然后通过重复的控制策略，使某个准则函数最优化，而每个 聚类由其质心来代表(k‐means 算法)，或者由该聚类中最靠近中心的一个对象来 代 表(k‐medoids 算法)。 划分聚类算法收敛速度快， 缺点在于它倾向于识别凸形分布 大小相近、密度相近的聚类，不能发现分布形状比较复杂的聚类，它要求类别数 目 k 可以合理地估计，并且初始中心的选择和噪声会对聚类结果产生很大影响。 主要的划分聚类算法有 k‐means，EM，k‐medoids，CLARA，CLARANS 等。 下面主要介绍 K‐means 聚类方法。 k‐means 算法首先随机选择 k 个对象，每个对象代表一个聚类的质心。对于其 余的每一个对象，根据该对象与各聚类质心之间的距离，把它分配到与之最相似 的聚类中。然后，计算每个聚类的新质心。重复上述过程，直到准则函数会聚。 通常采用的准则函数是平方误差准则函数(squared‐error criterion)，即 E i 1 pC p m
自组织特征神经网络简介
在人类的神经系统及脑的研究中，人们发现:人脑的某些区域对某种信息或 感觉敏感，如人脑的某一部分进行机械记忆特别有效;而某一部分进行抽象思维 特别有效。这种情况使人们对大脑的作用的整体性与局部性特征有所认识。对大 脑的研究说明，大脑是由大量协同作用的神经元群体组成的。大脑的神经网络是 一个十分复杂的反馈系统;在这个系统中含有各种反馈作用，有整体反馈，局部 反馈:另外，还有化学交互作用。在大脑处理信息的过程中，聚类是极其重要的 功能。大脑通过聚类过程从而识别外界的信号，并产生自组织过程。根据大脑对 信号的处理特点，在 1981 年，T.Kohonen 提出了一种神经网络模型，也就是自 组织特征映射 SOM(Self 一 orzanizingFeatureMap)。 SOM 网络算法是一种聚类算法，它能根据其学习规则对输入的模式进行自 动分类，即再在无监督的情况下，对输入模式进行自组织学习，通过反复地调整 连接权重系数，最终使得这些系数反映出输入样本之间地相互关系，并在竞争层 将分类结果表示出来。因此，SOM 神经网络在结构上模拟了大脑皮层中神经元 旱二维空间点阵的结构，并在功能上通过网学习功能。该算法被广泛应用于 各种模式识别和分类问题中。
问题探究
近年来，数据挖掘成为越来越热的一个研究方向，而聚类(clustering)作为数 据挖掘的主要方法之一，也越来越引起人们的关注。所谓聚类，就是把大量的 d 维数据对象(n 个)聚集成 k 个聚类(k<n)， 使同一聚类内对象的相似性尽可能最大，
而不同聚类内对象的相似性尽量达到最小。也就是说，形成聚类之后，同一个聚 类内对象具有很高的相似性， 而与不属于该聚类的对象有迥然的差异(即不相似)。 聚类与分类相比，分类算法分析的是类别已知的数据集，而聚类算法分析的是类 别未知的数据。 聚类的输入是一组未分类的记录，而且事先也不知道要分成几类，它通过分 析数据，根据一定的分类准则，合理划分记录集合，从而确定每个记录所属的类 别。不同的聚类算法中，用于描述相似性的函数也有所不同，有的采用欧氏距离 或马氏距离，有的采用向量夹角的余弦，也有的采用其他的度量方法。 当预先不知道类型数目， 或者用参数估计和非参数估计难以分辨不同类型的 类概率密度函数时，就需要采用聚类分析。有些聚类分析算法可以自动地确定类 型的数目 k，而不必以预知 k 为前提条件，也可以给定 k 作为算法的终止条件若 没有给定 k，那么如何在聚类过程中自动地确定 k，这是聚类分析中的一个关键 问题。 确定 k 值的方法很多，具体哪种较好还有待探究。基于自组织特征神经网络 （SOM）的聚类分析是其中的一种解决方案。
通过计算结果作图分析可以确定 k 值。再结合 k‐means 算法快速分类。 参考文献： 【1】 基于 SOM 神经网络和 K‐均值聚类的分类器设计 曹金平 【2】 基于自组织映射神经网络的低压故障电弧聚类分析 邹云峰，吴吴为麟李智勇 【3】 基于自组织特征映射网络的聚类算法研究 吴红艳 附录： k‐mean 和 SOM 神经网络 matlab 程序（未调试） 。