下载文档原格式
正弦定理和余弦定理的所有公式正弦定理和余弦定理的公式有哪些?在数学学习中，正弦定理和余弦定理的应用是很频繁的，正余弦定理指定是正弦定理、余弦定理,是揭示三角形边角关系的重要定理,下面是小编为大家整理的正弦定理和余弦定理的所有公式，供参考。
数学不好的人五大特征高中数学最无耻的得分技巧高考考场上数学拿高分的技巧如何判断函数的对称性与周期性1正弦定理、三角形面积公式正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，并且都等于该三角形外接圆的直径，即：a/sinA=b/sinB=c/sinC=2R.面积公式：S△=1/2bcsinA=1/2absinC=1/2acsinB.1.正弦定理的变形及应用变形：(1)a=2RsinA,b=2RsinB,c=2RsinC(2)sinA∶sinB∶sinC=a∶b∶c(3)sinA=a/2R,sinB=b/2R,sinC=c/2R.应用(1)利用正弦定理和三角形内角和定理，可以解决以下两类解斜三角形问题：a.已知两角和任一边，求其他两边和一角.b.已知两边和其中一边的对角，求另一边的对角.一般地，已知两边和其中一边的对角解三角形，有两解、一解.(2)正弦定理，可以用来判断三角形的形状.其主要功能是实现三角形中边角关系转化.例如：在判断三角形形状时，经常把a、b、c分别用2RsinA、2RsinB、2RsinC来代替.2.余弦定理在△ABC中，有a2=b2+c2-2bccosA;b2=c2+a2-2accosB;c2=a2+b2-2abcosC;变形公式：cosA=b2+c2-a2/2bc,cosB=c2+a2-b2/2ac,cosC=a2+b2-c2/2ab在三角形中，我们把三条边(a、b、c)和三个内角(A、B、C)称为六个基本元素，只要已知其中的三个元素(至少一个是边)，便。
三角形正弦余弦公式大全三角形是几何学中的一个重要概念，对于它的研究和应用有着广泛的需求。
在三角形的研究中，正弦和余弦公式是常用的工具，用于计算和解决各种三角形相关问题。
本文将详细介绍三角形正弦余弦公式并提供一些实例进行说明。
一、正弦公式在一个三角形ABC中，假设角A、B、C的对边分别为a、b、c，那么正弦公式可以表示为：sinA/a = sinB/b = sinC/c其中，sinA、sinB、sinC表示角A、B、C的正弦值，a、b、c表示对应边的长度。
正弦公式的应用非常广泛，可以用于求解三角形的各种边长和角度。
下面通过几个实例来说明正弦公式的具体应用。
实例1：已知一个三角形的两边长度分别为2厘米和3厘米，夹角为45度，求第三边的长度。
解：根据正弦公式有 sin45°/2 = sinC/c，即 sinC = (2/3)sin45°。
根据sin45°的值可以求得sinC的值，进而可以求得第三边的长度c。
实例2：已知一个三角形的两边长度分别为6厘米和8厘米，夹角为60度，求第三边的长度。
解：根据正弦公式有 sin60°/6 = sinC/8，即 sinC = (8/6)sin60°。
根据sin60°的值可以求得sinC的值，进而可以求得第三边的长度c。
二、余弦公式在一个三角形ABC中，假设角A、B、C的对边分别为a、b、c，那么余弦公式可以表示为：c² = a² + b² - 2abcosCa² = b² + c² - 2bccosAb² = a² + c² - 2accosB其中，cosA、cosB、cosC表示角A、B、C的余弦值。
余弦公式也是用于解决各种三角形问题的重要工具，可以通过已知的边长和角度来求解其他未知的边长和角度。
下面通过几个实例来说明余弦公式的具体应用。
正弦公式和余弦公式正弦公式和余弦公式是数学中最为重要的基本公式之一，研究正弦公式和余弦公式，可以让我们更深刻地理解数学世界。
1.弦公式的概念正弦公式是 sin x = y形式，其中，x变量，y其结果值， sin 正弦函数。
正弦公式是数学中最重要的公式之一，其应用非常广泛，常用于分析图形结构，可以简化许多复杂问题的解决方案。
许多测量，工程，科学研究领域中都可以看到它的影子。
正弦公式通过一定关系，将某个角度和它对应的正弦值确定，也就是sin x = y。
无论x如何变动，其正弦值都是不变的，可以用来对比不同角度下晃动幅度的大小，确定其最大值。
例如，在正弦曲线中，当角度为90度时，其所代表的正弦值最大，为1；当角度为180度时，其所代表的正弦值最小，为-1。
2. 余弦公式的概念余弦公式也叫做余裕函数，是cos x = y形式，其中，x 为变量，y 为其结果值，cos余弦函数。
余弦公式同样也是数学中重要的一种基本公式，主要应用于物理学方面。
余弦公式本质上与正弦公式类似，也是将某个角度和它对应的余弦值确定关系。
余弦公式也可以用来分析图形结构，通过余弦函数可以求出某个角度对应的余弦值，方便计算机做出正确的判断，达到准确解决问题的目的。
例如，利用余弦公式可以求出任意角度的余弦值，如角度为0度时，其余弦值为1、角度为90度时，其余弦值为0。
3.弦公式和余弦公式的用法1）正弦公式和余弦公式都可以用来分析图形，让我们可以快速地确定角度和正弦值或者余弦值之间的关系，从而方便计算机准确地运算并求解难题。
2）正弦公式和余弦公式也可以用于描述不同频率的波形，因此，它们也可以用来表示音频、视频等等。
3）正弦公式和余弦公式在求解一些物理学问题时也有着重要的作用，它们主要用于描述摆动的曲线和它们的行为规律，可以帮助我们探究解决各种复杂的物理问题。
4.弦公式和余弦公式的拓展正弦公式和余弦公式可以拓展到其他更高阶的公式上来，比如反正弦公式，反余弦公式等等。
正弦定理和余弦定理公式正弦定理是指在一个三角形ABC中，三角形的任意一个角a、b、c的正弦与相对应的边的比例相等，即：sin(a)/a = sin(b)/b = sin(c)/c其中a、b、c分别表示三角形的三个边长，A、B、C分别表示对应的角度。
根据正弦定理公式，我们可以推导出以下两个关系式：a/sin(A) = b/sin(B) = c/sin(C)A = arcsin(a/b*sin(B)) = arcsin(a/c*sin(C))B = arcsin(b/a*sin(A)) = arcsin(b/c*sin(C))C = arcsin(c/a*sin(A)) = arcsin(c/b*sin(B))这些关系式可以帮助我们在已知三角形的两个角度和一个边长的情况下，求解出其他未知的边长和角度。
正弦定理的应用：-在解决三角形边长和角度的问题时，特别是当已知一个角度和两个边长时，可以利用正弦定理来求解其他未知量。
-在几何学中，可以利用正弦定理来计算两个不相邻边的夹角。
余弦定理是用来计算一个三角形的任意一个角的余弦值的平方与其余两边长度的关系。
在一个三角形ABC中，余弦定理可以表达如下：c^2 = a^2 + b^2 - 2ab*cos(C)b^2 = a^2 + c^2 - 2ac*cos(B)a^2 = b^2 + c^2 - 2bc*cos(A)其中a、b、c分别表示三角形的三个边长，A、B、C分别表示对应的角度。
根据余弦定理公式，我们可以推导出以下两个关系式：cos(A) = (b^2 + c^2 - a^2) / 2bccos(B) = (a^2 + c^2 - b^2) / 2accos(C) = (a^2 + b^2 - c^2) / 2ab这些关系式可以帮助我们在已知三角形的三个边长的情况下，求解出三个角度的余弦值。
余弦定理的应用：-在解决三角形边长和角度的问题时，特别是当已知三个边长时，可以利用余弦定理来求解其他未知量。
正弦和余弦公式篇一：正弦和余弦公式是三角学中的基本公式，它们被广泛运用于各种数学和科学领域。
以下是正弦和余弦公式的正文和拓展:正文:正弦和余弦公式是三角学中的基本公式，它们可以用来计算三角形中的角度和边长。
正弦公式表示为:sinθ = 對數據數 (∫-180°/2πdθ)其中，θ是角度，對數據數是角度的对数。
余弦公式表示为:cosθ = 平氣據數 (∫-180°/2πdθ)其中，θ是角度，平氣據數是角度的对数。
拓展:正弦和余弦公式在各种数学和科学领域中都有广泛的应用。
以下是一些例子:1. 物理学：正弦和余弦公式可以用来计算弦的振动频率和波长。
2. 天文学：正弦和余弦公式可以用来计算行星的轨道大小和倾角。
3. 工程学：正弦和余弦公式可以用来计算机械振动的周期和振幅。
4. 计算机科学：正弦和余弦公式可以用来计算图形的亮度和颜色。
5. 物理学：余弦定理可以用来计算两个物体之间的引力和距离。
总结起来，正弦和余弦公式是三角学中的基本公式，它们在我们的日常生活中有着广泛的应用。
篇二：正弦和余弦公式是三角学中非常重要的公式，它们可以用来计算三角形中各种角度的正弦和余弦值。
以下是正弦和余弦公式的正文和拓展: 正文:正弦公式:sinθ = 對數× esinθ其中，對數表示半周長，esinθ表示正弦值。
余弦公式:cosθ = 對數× ecsθ其中，對數表示半周長，ecsθ表示余弦值。
拓展:正弦和余弦公式可以用于计算任何角度的正弦和余弦值。
假设角度θ是三角形中的角度，可以用以下公式来计算其正弦和余弦值:正弦值:sinθ = 對數× cos(90° - θ)其中，90° - θ表示角度θ的对角度。
余弦值:cosθ = 對數× sin(90° - θ)其中，90° - θ表示角度θ的对角度。
正弦和余弦公式也可以用于计算弦长和角度之间的关系。
正切与余切的转化公式
正切与余切是常用于数学中的两个类型的三角函数，它们之间有相互转化的公式。
在三角函数中，它们的关系非常重要，可以用来计算不同类型的三角函数的值。
正弦函数（Sin），余弦函数（Cos）和正切函数（Tan）是相互关联的函数，三角函数的结果可以使用它们来计算。
其中，正切函数tan(x)，定义为x对应的弧度值对应的正弦值除以余弦值。
余切函数cot(x)，定义为余弦值除以正弦值。
从理论上讲，正切与余切是相互等价的。
这意味着，任何一个函数的值可以通过转换成另外一个函数的值来计算，这称为“正切与余切的转化公式”。
其转化公式为：tan(x) = cot(x) = 1/tan(x) 。
由此可见，正切与余切是一对对立的函数，它们可以互相转化。
因此，从理论上讲，当知道一个三角函数的值时，可以利用正切与余切的转换公式来求出另一个三角函数的值，而无需繁琐的计算步骤。
同时，这对解决特定三角函数问题也是很有帮助的。
总之，正切与余切是理论上相互等价的，它们之间具有转换公式，这意味着可以用它们的转换公式来求解不同的三角函数，而不需要使用大量的计算步骤，这对解决数学问题是非常有用的。
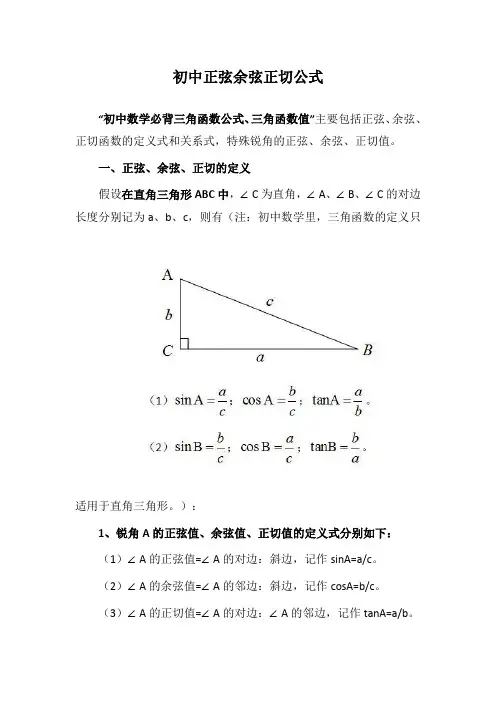
初中正弦余弦正切公式“初中数学必背三角函数公式、三角函数值”主要包括正弦、余弦、正切函数的定义式和关系式，特殊锐角的正弦、余弦、正切值。
一、正弦、余弦、正切的定义假设在直角三角形ABC中，∠C为直角，∠A、∠B、∠C的对边长度分别记为a、b、c，则有（注：初中数学里，三角函数的定义只适用于直角三角形。
）：1、锐角A的正弦值、余弦值、正切值的定义式分别如下：（1）∠A的正弦值=∠A的对边：斜边，记作sinA=a/c。
（2）∠A的余弦值=∠A的邻边：斜边，记作cosA=b/c。
（3）∠A的正切值=∠A的对边：∠A的邻边，记作tanA=a/b。
2、锐角B的正弦值、余弦值、正切值的定义式分别如下：（1）∠B的正弦值=∠B的对边：斜边，记作sinB=b/c。
（2）∠B的余弦值=∠B的邻边：斜边，记作cosB=a/c。
（3）∠B的正切值=∠B的对边：∠B的邻边，记作tanB=b/a。
【注】正弦=“对比斜”、余弦=“邻比斜”、正切=“对比邻”。
3、互余的两个角间的正弦、余弦、正切值关系假设在直角三角形ABC中，∠C为直角，则∠A与∠B互余。
通过∠A和∠B的正弦、余弦、正切值的定义式的对比，我们不难发现：∠A的正弦值与∠B的余弦值相等，∠A的余弦值与∠B的正弦值相等，∠A的正切值与∠B的正切值互为倒数。
所以，当∠A与∠B互余时我们有以下3个同时成立的等式关系：（1）sinA=cosB；（2）sinB=cosA；（3）tanA·tanB=1。
二、同角的正弦值、余弦值、正切值间的关系式1、商数关系：tanA=sinA/cosA；tanB=sinB/cosB.2、平方关系：同一个锐角的‘正弦的平方’与‘余弦的平方’的和为1，即(sinA)^2+(cosA)^2=1；(sinB)^2+(cosB)^2=1.3、倒数关系：tanA·cotA=1；tanB·cotB=1.【注】“cotA”称为为∠A的余切，它等于∠A的邻边比上∠A的对边。
正弦和余弦转换公式一:设α为任意角，终边相同的角的同一三角函数的值相等:sin(2kπ＋α）＝sinαcos（2kπ＋α)＝cosαtan(2kπ＋α）＝tanαcot(2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin(π＋α）＝－sinαcos(π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α)＝cotα公式三：任意角α与 -α的三角函数值之间的关系:sin（－α）＝－sinαcos(－α)＝cosαtan（－α)＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π—α与α的三角函数值之间的关系: sin（π－α)＝sinαcos（π－α）＝－cosαtan（π－α)＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π—α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α)＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot(π/2－α)＝tanα诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为：对于k·π/2±α(k∈Z)的个三角函数值，①当k是偶数时，得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值，即sin→cos;cos→sin;tan→cot，cot→tan。
（奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号.(符号看象限）例如：sin（2π－α）＝sin（4·π/2－α)，k＝4为偶数，所以取sinα。
