正弦和余弦的相互关系

正弦与余弦知识点总结正弦与余弦的定义在直角三角形中，如果一个锐角的对边和斜边的比值为正弦值，邻边和斜边的比值为余弦值。

假设在直角三角形ABC中，∠C为90°，AB为斜边，BC为对边，AC为邻边，那么正弦与余弦的定义如下：正弦值：sin∠A=对边/斜边=BC/AB余弦值：cos∠A=邻边/斜边=AC/AB在直角三角形中，正弦与余弦的值可以用来描述角度和三角形边长的关系。

在不同的三角形中，正弦与余弦的值并不相同，但其性质和图像是相似的。

正弦与余弦的性质1. 周期性：正弦与余弦函数都具有周期性，其周期为2π。

这意味着在一个周期内，函数值将重复出现。

在[-π, π]或[0, 2π]范围内，正弦与余弦的函数图像将呈现出周期性的特点。

2. 奇偶性：正弦函数是奇函数，余弦函数是偶函数。

奇函数具有对称中心原点，即f(-x)=-f(x)，在图像上关于原点对称。

而偶函数则具有对称中心y轴，即f(-x)=f(x)，在图像上关于y轴对称。

3. 交替性：正弦与余弦函数在图像上呈现出交替变化的特点。

在一个周期内，正弦函数的最大值为1，最小值为-1；余弦函数的最大值为1，最小值为-1。

两个函数的图像像是上下振荡的波形。

4. 相关性：正弦与余弦函数是相互关联的。

在直角三角形中，三角函数的相互关系可以由勾股定理推导出来。

sin²x + cos²x = 1是三角函数基本关系式，也称为三角恒等式。

正弦与余弦的图像正弦与余弦函数的图像是学习三角函数的重要内容之一。

它们的图像形状、周期性、奇偶性等特点对于理解三角函数的性质至关重要。

正弦函数的图像是一条连续的波纹状曲线，具有周期性、奇函数特点。

其图像在[-π, π]或[0, 2π]范围内呈现出从最小值-1到最大值1的振荡变化。

正弦函数的图像具有对称性，关于原点对称。

余弦函数的图像也是一条连续的波纹状曲线，具有周期性、偶函数特点。

其图像在[-π, π]或[0, 2π]范围内同样呈现出从最大值1到最小值-1的振荡变化。

初中数学什么是正弦和余弦正弦和余弦是初中数学中与三角函数相关的两个重要概念。

它们是用来描述和计算三角形中角度和边长之间关系的函数。

在本文中，我们将详细讨论正弦和余弦的定义、性质和应用。

一、正弦函数正弦函数是指一个角的正弦值与其对边与斜边的比值之间的关系。

具体来说，对于一个锐角A，它的正弦值定义为sin(A) = 对边/斜边。

对于钝角A，正弦值定义为sin(A) = -对边/斜边。

正弦函数具有以下几个重要的性质：1. 值域和定义域：正弦函数的值域为[-1, 1]，定义域为整个实数集。

2. 周期性质：正弦函数是周期函数，其最小正周期为2π，即sin(A) = sin(A + 2π)。

3. 对称性质：正弦函数是奇函数，即sin(-A) = -sin(A)。

4. 单调性质：在一个周期内，正弦函数在[0, π]上是单调递增的，在[π, 2π]上是单调递减的。

正弦函数在几何学中有着广泛的应用。

它可以用来计算和描述三角形中的角度和边长之间的关系，比如计算角度的正弦值、计算边长的比例等。

此外，正弦函数还可以用来解决关于周期性和周期函数的问题，比如计算函数的周期、求解方程等。

二、余弦函数余弦函数是指一个角的余弦值与其邻边与斜边的比值之间的关系。

具体来说，对于一个锐角A，它的余弦值定义为cos(A) = 邻边/斜边。

对于钝角A，余弦值定义为cos(A) = -邻边/斜边。

余弦函数具有以下几个重要的性质：1. 值域和定义域：余弦函数的值域为[-1, 1]，定义域为整个实数集。

2. 周期性质：余弦函数是周期函数，其最小正周期为2π，即cos(A) = cos(A + 2π)。

3. 对称性质：余弦函数是偶函数，即cos(-A) = cos(A)。

4. 单调性质：在一个周期内，余弦函数在[0, π/2]上是单调递减的，在[π/2, 3π/2]上是单调递增的。

余弦函数在几何学中有着广泛的应用。

它可以用来计算和描述三角形中的角度和边长之间的关系，比如计算角度的余弦值、计算边长的比例等。

正弦定理的概念与余弦定理的概念正弦定理和余弦定理是在三角形中用于计算边长和角度的重要定理。

1. 正弦定理（Sine Rule）：正弦定理是用来计算三角形中的边长和角度的关系。

对于一个三角形ABC，正弦定理可以表述为：
a/sinA = b/sinB = c/sinC
其中a、b、c分别表示三角形的边长，A、B、C分别表示对应边的角度。

2. 余弦定理（Cosine Rule）：余弦定理是用来计算三角形中的边长和角度的关系。

对于一个三角形ABC，余弦定理可以表述为：
c^2 = a^2 + b^2 - 2abcosC
其中a、b、c分别表示三角形的边长，C表示对应边的角度。

正弦定理和余弦定理都可以在解决三角形问题时使用，它们提供了计算边长和角度的方法，可以帮助我们求解各种三角形相关的问题。

正弦和余弦公式正弦和余弦公式是一种广泛应用于三角函数中的基本运算法则。

正弦函数(sin)和余弦函数(cos)是一对基本的数学公式，广泛应用于各类数学计算中，包括解三角形问题、优化问题、计算复杂数学表达式等。

它们的关系可以通过单位圆来直观地理解：正弦函数表示单位圆上点的纵坐标，余弦函数表示单位圆上点的横坐标。

正弦公式sin(α±β) = sinαcosβ ± cosαsinβ、sin2α = 2sinαcosα、sinαsinβ =1/2[cos(α - β) - cos(α + β)]都是正弦函数的固有运算法则。

余弦公式cos(α±β) = cosαcosβ ∓ sinαsinβ、cos2α = cos²α - sin²α = 2cos²α - 1 = 1 - 2sin²α、cosαcosβ = 1/2[cos(α + β) + cos(α - β)]都是余弦函数的固有运算规则。

正弦和余弦公式在物理、工程、经济等众多领域都有着广泛的应用。

例如，在物理学中，振动和波动问题常常需要用到正弦和余弦公式进行描述和计算。

在工程学中，许多复杂的力学问题也会通过正弦和余弦公式进行化简和求解。

值得注意的是，正弦和余弦公式在运算过程中，往往需要注意角度的转换问题。

在实际应用中，角度一般有两种表示方式：度数制和弧度制。

当我们在使用正弦和余弦公式时，需要根据具体的情况，清楚地知道角度是以何种形式表示的，否则可能会导致计算错误。

总的来说，正弦和余弦公式是数学的基础知识，良好的掌握和理解能够帮助我们更好的解决各类数学相关问题。

同时，它们作为一种普遍的数学语言，也是我们理解世界的重要工具。

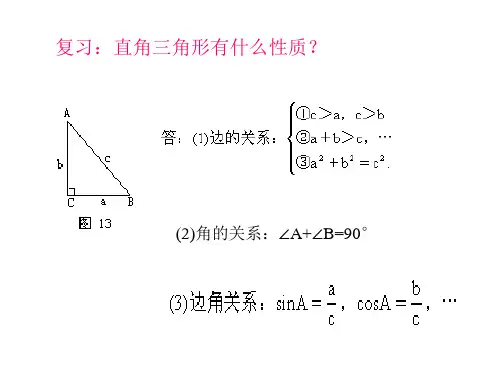
浅谈正弦定理与余弦定理的等价性
1 正弦定理与余弦定理
正弦定理与余弦定理是数学中两个重要定理，它们都可以用来求出在等边三角形中求对边相互关系，也可以求出三角形的面积。

这两个定理具有十分重要的等价性。

1.1 正弦定理
正弦定理可以用以下公式表示：sinA/a=sinB/b=sinC/c，其中A,B,C 为三角形的三个内角，a，b，c为三角形的三条边长。

这一定理是由欧几里德在他的几何元素中提出的，用来求出等边三角形中各个边的长度比例关系。

1.2 余弦定理
余弦定理可以表述为以下公式：a2=b2+c2-2bc cosA，其中A,B,C 为三角形的三个内角，a，b，c为三角形的三条边长。

该定理也是欧几里德在几何元素中提出的，它可以用来求出等边三角形中各边之间的夹角大小或者是求出三角形的面积。

2 等价性
由正弦定理和余弦定理的定义可以看出，它们之间具有一种等价性，它们都可以用来求出三角形的面积。

通过把余弦定理中的右端用二项式展开式表示，就可以解释出正弦定理与余弦定理的等价性。

这也就是说，在求解三角形时，可以用正弦定理求出对应的边之间的长度比例和夹角大小，再根据它们求出三角形的面积；或者是直接用余弦定理，然后用二项式展开式求出面积。

3 结论
从上述讨论可以看出，正弦定理与余弦定理有着一定的等价性，它们在求解三角形的面积方面具有相同的效果，只是表示方式不一样而已。

用任何一个定理都可以精确的求出相应的三角形的面积，这就是正弦定理与余弦定理的等价性所在。

三角形的正弦余弦正切关系三角形的正弦、余弦、正切关系三角形是几何学中常见的形状，而正弦、余弦和正切则是与三角形密切相关的三个三角函数。

这些三角函数提供了三角形边角关系的重要信息，有助于求解三角形的各种属性和问题。

在本文中，我们将探讨三角形的正弦、余弦和正切关系，并讨论它们在数学和实际应用中的重要性。

1. 正弦关系正弦函数是最常见的三角函数之一，它用于描述角度与其对边长度之间的关系。

在任意三角形ABC中，假设∠A为一个角度，a、b和c分别为与之对应的边长。

那么，我们可以定义三角形的正弦关系如下：sin(∠A) = a/c这意味着正弦函数的值等于角度∠A的对边长度与斜边长度的比值。

通过这个关系，我们可以在已知两个边长的情况下，求解三角形的未知边长或角度。

2. 余弦关系余弦函数也是常用的三角函数，它描述角度与其邻边长度之间的关系。

在同样的三角形ABC中，我们可以定义三角形的余弦关系如下：cos(∠A) = b/c这意味着余弦函数的值等于角度∠A的邻边长度与斜边长度的比值。

通过这个关系，我们可以在已知一边和斜边的情况下，求解三角形的其他边长或角度。

3. 正切关系正切函数是用来描述角度与其邻边与对边的比值关系的三角函数。

在同样的三角形ABC中，我们可以定义三角形的正切关系如下：tan(∠A) = a/b这意味着正切函数的值等于角度∠A的对边长度与邻边长度的比值。

通过这个关系，我们可以在已知邻边和对边的情况下，求解三角形的其他边长或角度。

综上所述，三角形的正弦、余弦和正切关系提供了角度与边长之间的重要联系。

通过这些关系，我们可以在已知一些限定条件的情况下，求解三角形的未知属性。

这在数学和物理学中具有广泛的应用。

例如，在三角测量中，我们可以利用正弦、余弦和正切关系来测量难以直接获得的距离、高度或角度。

此外，这些三角函数的关系也在计算机图形学、机械工程和天文学等领域中扮演重要角色。

通过利用计算机技术和数值方法，我们可以利用这些关系来模拟和计算复杂的三角形形状，以及它们在实际场景中的各种属性和变化。

正弦余弦和正切之间的关系正弦、余弦和正切是三角函数中最基本的三种函数，它们之间存在着密切的关系。

首先，我们来看它们的定义和计算方法。

正弦函数（sin）表示一个角的对边与斜边的比值，通常用a/h表示，其中a为对边，h为斜边。

余弦函数（cos）表示一个角的邻边与斜边的比值，通常用b/h表示，其中b为邻边。

正切函数（tan）表示一个角的对边与邻边的比值，通常用a/b表示。

这三个函数之间的关系可以通过三角恒等式来描述。

例如，tanθ = sinθ / cosθ，这意味着正切函数可以表示为正弦函数与余弦函数的比值。

另外，我们还可以通过sin²θ + cos²θ = 1这一三角恒等式得到sinθ与cosθ之间的关系，进而推导出tanθ与sinθ、cosθ之间的关系。

在三角函数的图像中，我们也可以清晰地看到它们之间的关系。

正弦函数的图像是一个周期性的波浪曲线，而余弦函数的图像则是正弦函数图像的相位延迟π/2。

正切函数的图像则是在余弦函数的零点处具有无穷大的间断点，这也反映了正切函数与正弦、余弦之间的关系。

除了上述数学关系和图像特点外，正弦、余弦和正切在实际问题中也有着丰富的应用。

在三角测量、物理学、工程学等领域，这三种函数经常被用来描述角度、振动、周期性变化等现象，它们之间的关系也为解决实际问题提供了重要的数学工具。

综上所述，正弦、余弦和正切之间存在着密切的数学关系，可以通过三角恒等式、图像特点和实际应用来全面理解它们之间的联系。

这些函数的相互关系不仅在数学领域具有重要意义，也在实际问题的求解中发挥着重要作用。

三角函数中的正弦定理与余弦定理主题：三角函数中的正弦定理与余弦定理引言：三角函数是数学中重要的概念之一，它们在几何、物理等领域广泛应用。

在三角函数中，正弦定理与余弦定理是两个重要的定理，它们可以帮助我们计算三角形的边长和角度。

本教案将介绍正弦定理与余弦定理的原理和应用。

一、正弦定理的原理与应用1. 原理正弦定理是指在任意三角形ABC中，三边的长度a、b、c与相应的角A、B、C之间满足如下关系：sin A / a = sin B / b = sin C / c2. 推导通过推导可以得到正弦定理的证明过程，但是本教案不涉及具体推导过程。

3. 应用正弦定理在解决三角形问题中有广泛的应用，例如可以用来计算未知边长或角度。

通过给定的已知信息，利用正弦定理可以求解三角形的各个角度和边长。

二、余弦定理的原理与应用1. 原理余弦定理是指在任意三角形ABC中，三边的长度a、b、c与相应的角A、B、C之间满足如下关系：c^2 = a^2 + b^2 - 2ab * cos C2. 推导通过推导可以得到余弦定理的证明过程，但是本教案不涉及具体推导过程。

3. 应用余弦定理也在解决三角形问题中有广泛的应用，它可以用来计算未知边长或角度。

通过给定的已知信息，利用余弦定理可以求解三角形的各个角度和边长。

三、正弦定理与余弦定理的比较1. 区别正弦定理与余弦定理在表达形式上有所不同，前者是通过比例关系来描述，后者是通过角度和边长的平方和相互联系。

2. 应用场景正弦定理适用于解决未知边长或角度的问题，特别是在已知两个角和一个边长的情况下比较有用。

而余弦定理适用于计算三角形的边长，特别适合已知三个边长和一个角度的情况。

四、实例分析通过几个实例来演示正弦定理与余弦定理在解决三角形问题中的应用。

这些实例可以帮助学生更好地理解和掌握这两个定理的用法和原理。

小结：正弦定理与余弦定理是解决三角形问题中的重要工具。

了解它们的原理和应用可以帮助学生在解决实际问题时得到准确的答案。

正弦余弦正切三者之间的关系
近年来，文化的多元发展，越来越多的人开始了解相关的数学知识。

其中，正弦余弦正切都是许多学生们关注和学习的知识点。

它们是非常有用的数学公式，能帮助人们更加直观地理解数学中的概念。

首先，正弦是函数y=sin x的简称，它代表一段遵循弧度的线段，用角度表示可以用弧度的长度来表示，在数学中它可以用来表示三角形中任意角的正弦值。

其次，余弦是函数y=cos x的简称，它可以用来表示和正弦函数相互呼应的形态变化。

它表示三角形中角度的余弦值，比较它和正弦函数，就可以很容易地理解它们之间的关系。

最后，正切可以用来表示函数y=tan x，它是用来表示三角形中任意角的正切值，这就意味着它和正弦以及余弦都是密不可分的。

正弦余弦正切三者之间的关系就是这样，它们三者的变化相互关联，结合使用才能够更好地实践理论，真正让你有效理解数学中的概念。

所以，学生们应该大力学习这三者的相关知识，这将有助于日后的学习和生活工作。

三角函数正弦与余弦的关系嘿，朋友们，今天咱们聊聊三角函数里的正弦和余弦，简单说就是Sine 和Cosine，这两个家伙真是关系密切得不得了，像老搭档一样，形影不离。

你知道吗？它们就像那对无话不谈的好朋友，真是个妙不可言的组合。

要说正弦和余弦，最简单的就是把它们想象成一个坐标系里的小伙伴，一个在X 轴上，一个在Y 轴上，两个小家伙相互依赖，缺一不可。

咱们来聊聊正弦。

正弦，哦，那可是个大名鼎鼎的家伙，它负责的是Y 轴上的值，真是太重要了，没了它，图形就像失去了灵魂。

你想想，正弦的值，随着角度的变化而变化，像是在做快乐的舞蹈，随着角度的增加，它有时候高兴得翘起了头，有时候又低下了脑袋，真是变化多端，让人捉摸不透。

可你知道吗？正弦的值只会在 1 到 1 之间跳来跳去，这就像是那孩子，在游乐场里，虽然跑得欢，但永远不可能跳出围栏。

再说说余弦，这小子可不甘示弱，它负责的是 X 轴上的值。

余弦和正弦就像两口子，一个负责大气，一个照顾家务，默契得不行。

余弦也是随着角度而变化，感觉它有时候像个开朗的小太阳，咧嘴大笑，有时候又像个闷闷不乐的小雨点，真是情绪波动得厉害。

不过，余弦的值同样也是被限制在1 到1 之间，这可不是什么随心所欲的事儿，得在这两个极端之间打转。

有趣的是，正弦和余弦有一个特别的关系，它们总是成对出现，这就像是咱们生活中的好朋友，总是一起行动。

你看，正弦的值可以通过余弦的值轻松算出来，只需要找出对应的角度，简单吧？就像你在朋友那儿借书，总能借到想看的那一本。

再说了，如果把它们放在单位圆上，正弦就成了 Y 轴的坐标，而余弦就是 X 轴的坐标，像两个紧紧相拥的好伙伴，互相守护，互相照应。

说到这里，可能有人会问，这两个家伙有什么用呢？哦，别急，听我慢慢说。

它们可不仅仅是数学课本里的冷冰冰的数字，而是实际生活中无处不在的影子。

你想，音乐、物理、工程，甚至是你手机里的 GPS，都是在用到这些三角函数。

比如说，音乐里的音调变化，就是在正弦波和余弦波之间摇摆的。

推导直角三角形的正弦定理与余弦定理直角三角形是指其中一角为90度的三角形，由于其特殊性质，我们可以通过推导得出直角三角形的正弦定理和余弦定理。

下面将分别介绍这两个定理的推导过程。

正弦定理的推导：考虑一个直角三角形ABC，其中∠B为直角。

设AB=c，AC=b，BC=a，以及∠CAB为θ。

根据正弦定理，有以下关系：sin(θ) = a/c为了推导出这个关系，我们可以使用三角形的辅助线。

首先，我们在三角形ABC中，从点C向AB引一条垂线CD。

根据垂直角的性质，可以得到∠CDA=90-θ。

接下来，我们观察三角形ACD，根据三角形中的角的和为180度的性质，可以得到∠CDA + ∠CAD + ∠ACD = 180度。

由于∠CDA=90-θ且∠CAD=90度，代入上述公式可得：(90-θ) + 90 + ∠ACD = 180度化简得到∠ACD=θ。

现在，我们观察三角形ACD和ABC的对应边长，根据正弦定理可得：sin(θ) = CD/AC = CD/bsin(θ) = a/c因此，我们成功地推导出了直角三角形的正弦定理。

余弦定理的推导：同样考虑一个直角三角形ABC，其中∠B为直角。

设AB=c，AC=b，BC=a，以及∠CAB为θ。

根据余弦定理，有以下关系：c^2 = a^2 + b^2为了推导出这个关系，我们再次使用三角形的辅助线。

我们在三角形ABC的斜边AC上选取一点D，使得AD为c的垂线。

根据垂直角的性质，可以得到∠CAD=θ。

接下来，我们观察三角形ACD，并使用勾股定理得到以下的关系：AC^2 = AD^2 + CD^2代入已知数据，可得：c^2 = AD^2 + CD^2我们可以通过观察发现AD=a，且CD=b。

代入上式，得到：c^2 = a^2 + b^2因此，我们成功地推导出了直角三角形的余弦定理。

综上所述，我们通过对直角三角形的辅助线和勾股定理的应用，成功地推导出了直角三角形的正弦定理和余弦定理。

三角函数与函数的联系在数学中，三角函数是一类重要的函数，它们与其他类型的函数之间存在着密切的联系。

本文将探讨三角函数与函数的关系，并介绍一些主要的三角函数和它们的性质。

一、正弦函数与函数的联系正弦函数是最基本的三角函数之一，它在数学和物理学中都有广泛的应用。

正弦函数可以表示为y = sin(x)，其中x为自变量，y为因变量。

这种函数通常用来描述周期性现象，如波动、震动等。

正弦函数与其他类型的函数之间存在着密切的联系。

例如，正弦函数可以与线性函数相乘，得到新的函数形式。

这种形式被广泛应用于信号处理和通信领域，用于调制和解调信号。

正弦函数还可以与指数函数、对数函数、幂函数等进行组合，形成更复杂的函数。

二、余弦函数与函数的联系余弦函数是另一种常见的三角函数，它可以表示为y = cos(x)，其中x为自变量，y为因变量。

余弦函数与正弦函数非常相似，但它们在波形上存在相位差。

余弦函数通常用于描述旋转或振动的运动规律。

与正弦函数类似，余弦函数也可以与其他类型的函数相乘、组合，形成更复杂的函数形式。

例如，在物理学中，余弦函数常用于描述振动系统的运动方程。

三、正切函数与函数的联系正切函数是三角函数中的另一个重要分支，它可以表示为y = tan(x)，其中x为自变量，y为因变量。

正切函数与正弦函数和余弦函数的关系可以通过以下公式表示：tan(x) = sin(x) / cos(x)。

正切函数在数学和物理学中也有广泛的应用。

正切函数可以与其他类型的函数相乘、组合，形成新的函数形式。

例如，在工程学和物理学中，正切函数常用于描述角度和斜率的关系。

四、反除了上述的三角函数之外，还存在着反三角函数，它们与三角函数之间有着紧密的联系。

反三角函数可以用来求解三角函数的反函数，并且可以与其他类型的函数进行组合。

常见的反三角函数包括反正弦函数（arcsin）、反余弦函数（arccos）和反正切函数（arctan）。

通过这些函数，我们可以得到对应的角度值，从而求解复杂的三角函数方程。

互余两角的正余弦之间的关系互余两角是指两个角的正弦和余弦相互对应相等的关系。

在三角函数中，正弦和余弦是最基本的函数之一，它们在数学和物理等领域中都有广泛的应用。

正弦函数（sine function）是一个周期函数，它描述了一个波动的过程。

在单位圆上，正弦函数的值等于对应角的纵坐标值。

而余弦函数（cosine function）也是一个周期函数，它描述了一个振动的过程。

在单位圆上，余弦函数的值等于对应角的横坐标值。

在三角函数中，互余两角的正余弦之间存在一种特殊的关系。

我们可以通过互余两角的定义和三角函数的性质来推导这种关系。

假设有两个互余角A和B，它们的正余弦分别为sin(A)，cos(A)，sin(B)，cos(B)。

根据互余两角的定义，我们知道：sin(A) = cos(B)，cos(A) = sin(B)现在我们来证明这个关系。

根据三角函数的定义，我们知道：sin(A) = 对边/斜边，cos(A) = 邻边/斜边sin(B) = 对边/斜边，cos(B) = 邻边/斜边由于A和B是互余角，那么它们的对边和邻边分别相等。

所以我们可以得到：对边A = 对边B，邻边A = 邻边B将这些条件代入正弦和余弦的定义中，我们可以得到：sin(A) = 对边B/斜边，cos(A) = 邻边B/斜边sin(B) = 对边A/斜边，cos(B) = 邻边A/斜边通过比较这些式子，我们可以发现：sin(A) = cos(B)，cos(A) = sin(B)这就证明了互余两角的正余弦之间存在一种特殊的关系。

互余两角的关系在三角函数的应用中有着重要的作用。

例如，在直角三角形中，如果我们已知一个角的正弦或余弦值，就可以通过互余两角的关系来求解其他角的正余弦值。

这在测量和计算中具有重要的实际意义。

在波动和振动的描述中，互余两角的关系也起到了重要的作用。

例如，在交流电路中，正弦函数被广泛用于描述电流和电压的变化规律。

而余弦函数则常常用于描述位移和速度的变化规律。