下载文档原格式
互为余角的两个角的正弦和余弦的关系互为余角的两个角是指它们的和为90度的两个角。
在三角函数中，正弦和余弦是两个重要的函数，它们与角的关系十分密切。
本文将探讨互为余角的两个角的正弦和余弦的关系。
我们先来回顾一下正弦和余弦的定义。
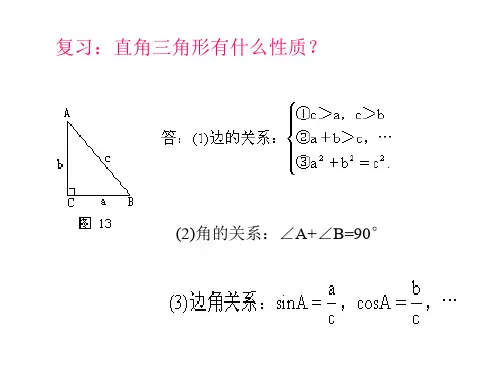
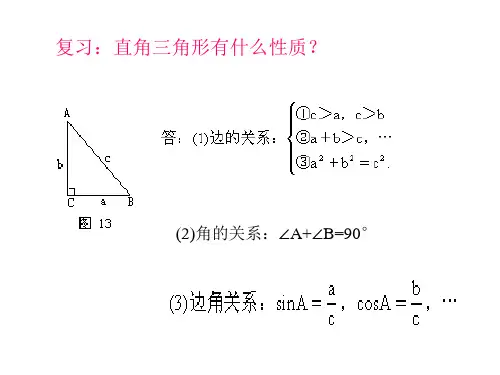
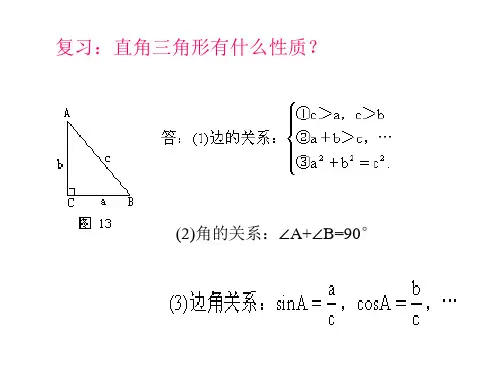
在一个直角三角形中，我们可以定义一个角的正弦为对边与斜边的比值，即sinA = a/c；而余弦则是邻边与斜边的比值，即cosA = b/c。
这里的A表示角的度数，a、b和c分别表示对边、邻边和斜边的长度。
接下来，我们考虑两个互为余角的角A和B。
根据余角的定义，A 和B的和为90度。
假设A的度数为x，那么B的度数就是90-x。
我们先来看互为余角的两个角的正弦关系。
根据正弦的定义，sinA = a/c，sinB = b/c。
由于互为余角的两个角A和B的和为90度，所以它们的斜边c是相等的。
这样，我们可以得到sinA = a/c = a/c = cosB。
换句话说，互为余角的两个角的正弦相等。
再来看互为余角的两个角的余弦关系。
根据余弦的定义，cosA = b/c，cosB = a/c。
同样地，由于互为余角的两个角A和B的和为90度，所以它们的斜边c是相等的。
这样，我们可以得到cosA = b/c = b/c = sinB。
换句话说，互为余角的两个角的余弦相等。
互为余角的两个角的正弦和余弦具有相等的特点。
这个结论可以用公式sinA = cosB和cosA = sinB来表示。
接下来，让我们通过一个具体的例子来验证这个结论。
假设角A的度数为30度，那么角B的度数就是90-30=60度。
根据三角函数的定义，我们可以计算出sin30° = 1/2，cos30° = √3/2，sin60° = √3/2，cos60° = 1/2。
可以看到，sin30° = cos60°，cos30° = sin60°，符合我们上面得出的结论。
互补和互余正弦和余弦的关系
两个角互余，则sinα=cosβ，cosα=sinβ。
两个角回互补，则sinα=sinβ，cosα=-cosβ。
在同一平面内，如果两个不重合的且有同一顶角的两个角相加等于180度，那么我们称这两个角互补（互为补角）。
若两角之和为90°，则称这两个角“互为余角”，简称“互余”。
三角函数简介
三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。
在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。
常见的三角函数包括正弦函数、余弦函数和正切函数。
在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。
不同的三角函数之间的关系可以通过几何直观或者计算得出，称为三角恒等式。
