消点法在几何中应用(二)
- 格式:pdf
- 大小:655.30 KB
- 文档页数:3

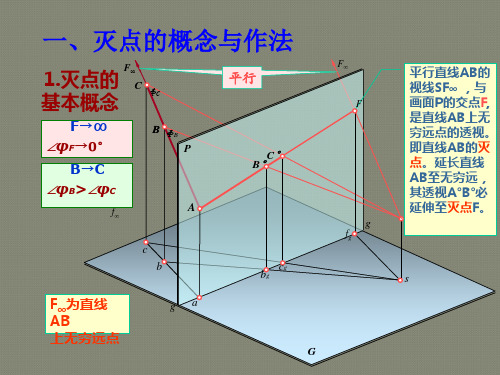
第五章灭点法作建筑透视图§5-3 透视平面图§5-4 灭点的一般通则 §5-5 建筑细部的透视图§5-1 灭点的概念与作法§5-2 用灭点法作建筑形体透视图§5-1 灭点的概念与作法一、直线灭点的基本概念二、水平线的灭点三、用灭点法求水平线的透视四、用灭点法求矩形平面的透视一、直线灭点的基本概念FfFfF二、水平线的灭点FFNfn三、用灭点法求水平线AB的透视La p bpB°A°b°a°FfsNn四、用灭点法求矩形平面的透视C °Ad p D °NF xf xb p B °F yf yn§5-2 用灭点法作建筑形体透视图一、求长方体的两点透视二、求组合长方体的两点透视三、纪念碑的二点透视四、求建筑形体的一点透视五、求两坡顶房屋的两点透视六、求室内形体的一点透视七、求阳台和挑檐的两点透视一、求长方体的两点透视LC °AF xf xF yf yd pD °d °b pB °b °Hxy Pg 'sHg 'c (c )P a (a )b (b )d (d )二、求组合长方体的两点透视nC °c pc °b p B ° b °3p 3° E °D °G °aF xf xF yf ybxyd ecg1243e ° d °g ° A °1p1°2p 2° 4p4° n三、纪念碑的二点透视d ° aa F yf ybedcmN 1n 1nn E °m °M ° C °c °B °b ° Am pe pc p b p D °F xf x四、求建筑形体的一点透视 C ° c p c ° a c 'd ' d ' c ' b ' 平面图立面图 s ' e p e ° E ° D ° d p d ° f p f ° B ° b p b ° g ' g ' H 透视图 G ° g p g ° Pgbf1 2 3 e c dPa b 'H g ' g ' a ' 1'a 'c ' 2'3' Hd '(e ') d '(e ') a '(g ')五、求两坡顶房屋的两点透视 F y E °j ° J ° B ° c ° C ° F x edc bjl ka A a °1 Ⅰ k ° K ° l ° L ° f x f y2 e p j p b p k p l pc p 1 2 Ⅱ P HP H g ' b a sg ' cd j ke a ' a 's六、求室内形体的一点透视真高线真高线七、求阳台和挑檐的两点透视d j abc e k hgm 1° 2° 3°4° 6°5° 8°7°F yF x f x f y b p a p c p e p k p g p m ph p b' d' j' a' c' e' k' g' m'h'§5-3 透视平面图一、透视平面图的作图原理二、透视平面图的作图方法三、两坡顶房屋的两点透视四、建筑形体的一点的透视五、建筑形体的透视平面图六、利用透视平面图作建筑形体的一点透视一、透视平面图的作图原理B ° b Pb p a b ° SsH AHBg g 1 G 1b 1 g b 1°a 1°二、透视平面图的作图方法b 1°g ' g ' B °bb p a b °s HH A F x H HF y g ' g ' a三、两坡顶房屋的两点透视 C ° 2°1n 2n 3 n 1 b p m p F 1L ° e ° a A ° n 4N 4 1°1 e °1 m °1 c °1 a °1 n 51 n 11 n 41 n 31 n 21 b °1f °1k °1L °1 F ° K ° b °B ° D ° F y F x f y f x M ° 侧立面图 平面图 g 'g ' g ' Hk "(l ")A "m "(2") d "(c ") g ' a " H s 2b f1l ec d aP n 5 n 4 P m四、建筑形体的一点的透视D °d p d ° C ° c pb p B ° E ° e p A ° a p a ° 透视平面图侧立面图 平面图 bP ecdg ' aP g 'HHs '五、建筑形体的透视平面图 dn 4n 3 n 1 n 2 n 6 n 5 bca1︒1 1p e ︒1 a p a ︒1b p b ︒1c p c ︒1d ︒1d p 1e 侧立面图平面图六、利用透视平面图作建筑形体的一点透视1︒C ° c ︒1E °e ︒1 d ︒1 D ° 1︒1A ° a °a ︒1b ︒1B °§5-4 灭点的一般通则§5-5 建筑细部的透视图一、门洞的透视二、窗洞的透视三、台阶的二点的透视四、用视线法作阳台和挑檐的透视五、用视线法作建筑物的一点透视一、门洞的透视 F °f ︒E ° D °C ° A °a ° He ︒d ︒n n a bfcd e B °b ° F y n 4 n 3 n 1n 2 n 6 n 5 F xN 1 n 1 n 3 N 3 n 5 N 5f y f x平面图二、窗洞的透视C °b ︒ n n aD ° d ° P PB ° E ° H Ac ︒ g ' H F ︒ f ° g 'G ° g °真高线真高线 真高线 真高线 剖面图 透视图 平面图F xF y f y f x s b cd e N 1 n 1 N 3 n 3N 2n 2a 1 1 e pa d p n 3 n 1b p n 2c p三、台阶的二点的透视3" 2" 1" a bc defghd p b p c pe pf p h pg p F °E ° G °H °h ° g ° f ° e ° 1 A 1 2 3A b ° D ° d ° c C °B ° 真高线 F yF xf x f y四、用视线法作阳台和挑檐的透视d j abc e k hgm 1° 2° 3°4° 6°5° 8°7°F yF x f x f y b p a p c p e p k p g p m ph p b' d' j' a' c' e' k' g' m'h'五、用视线法作建筑物的一点透视真高线真高线本章结束。

人工智能,几何定理机器证明的消点法人工智能在数学领域的应用越来越广泛,其中一项重要的应用就是几何定理的机器证明。
几何定理是数学中的重要内容,通过机器证明可以更加高效地验证和推导几何定理。
本文将以几何定理机器证明的消点法为主题,探讨人工智能在几何定理机器证明中的应用和优势。
在几何学中,点是最基本的几何概念之一。
消点法是一种常用的证明方法,通过消去某些点或线,从而简化几何问题的证明。
传统的消点法通常需要人工进行推导和计算,耗时且容易出错。
而借助人工智能技术,可以将消点法的推导过程交给机器来完成,大大提高了证明的效率和准确性。
机器证明的消点法基于数学逻辑和推理算法。
首先,机器需要对几何定理的条件和结论进行形式化表示,将其转化为逻辑表达式。
然后,机器利用数学公理和推理规则,通过逻辑推理来证明几何定理。
在证明过程中,机器会根据需要进行点的消去操作,简化几何问题的结构,从而更好地理解和推导几何定理。
相比传统的消点法,机器证明具有以下优势。
首先,机器证明可以高效地处理大量的几何问题,大大节省了人力和时间成本。
其次,机器证明的结果具有较高的准确性和可靠性,避免了人为推导中可能出现的错误。
此外,机器证明还可以发现一些不易察觉的几何性质和关系,为几何学的深入研究提供了新的思路和方法。
机器证明的消点法在实际应用中已经取得了一些重要的成果。
例如,通过机器证明的消点法,可以证明平面几何中的勾股定理。
勾股定理是三角学中的基本定理,传统的证明方法需要人工进行复杂的推导和计算。
而机器证明的消点法可以简化证明过程,减少推导的步骤,从而更加清晰地展示勾股定理的证明过程。
另一个应用是机器证明的消点法可以证明角平分线定理。
角平分线定理是几何学中的重要定理之一,传统的证明方法需要进行复杂的角度计算和线段垂直性的证明。
借助机器证明的消点法,可以简化证明过程,更加直观地展示角平分线定理的证明思路。
除了以上两个例子,机器证明的消点法还可以应用于其他几何定理的证明中。

消点三角法
消点法是一种解决几何问题的方法,特别是在涉及三角形时。
它的核心思想是通过逐步消除问题中的未知数,将复杂的问题转化为简单的问题,进而解决。
在涉及三角形的无损消点问题中,这种方法的计算往往比较复杂,不易被理解和接受。
具体来说,消点法可以应用于解决三角形中的各种问题,例如证明边长相等、角度相等、面积相等等等。
它的一般步骤是:
1. 根据问题的具体要求,选取合适的点和线段作为已知条件,将它们放在适当的位置上。
2. 通过构造平行线、延长线段、利用等腰三角形性质等方法,逐步消除问题中的未知数。
3. 在消除未知数的过程中,利用已知条件和几何定理进行推理和证明,最终得出结论。
值得注意的是,消点法虽然在一些情况下可能非常复杂和困难,但它的广泛应用证明它是非常有效的解题方法。
同时,通过不断地练习和掌握一些常用的几何定理和性质,可以更好地应用消点法解决几何问题。

“消点法”在初中几何解题的初探【摘要】历史上数学家在解几何中一直寻找着像解代数一样的通用公式,直到近代机器的发明,这样的系统才得以快速发展,我国数学家张景中院士以他的面积法发展起来的消点法使得机器证明几何得以实现。
本文就简单介绍此法在中学几何中用纸笔解题的应用。
【关键词】几何;机器证明;消点法在数学的历史长河中,数学家一直都希望像解代数一样为几何问题寻找一套公式,使得解几何像解代数问题一样套用公式,数学大师笛卡尔、莱布尼茨、希尔伯特等科学巨匠为此曾付出大量心血,但未能找到有效的途径。
而今特别是现在电子计算机的出现,人们更希望机器能代替人类成批地解决几何问题。
电子计算机的出现,大大促进了此领域的发展,早在50年代,美国数学家阿尔弗雷德?塔斯基就用代数方法证明初等几何机械化的可能性,但直到70年代,这种方法仍未曾得到很好的发展。
在这种以机器证明几何问题思维研究的发展中,我国的张景中院士以他多年来研究并发展的几何新方法(面积法)为基本工具,提出了消点法思想,并且和周咸山、高小山合作,于1992年突破了这项难题,从而实现了几何定理可读性证明的自动生成,此法不以坐标为基础,也不同于传统的综合方法,此方法以几何不变为前提,把几何、代数逻辑和人工智能方法结合起来所形成的开发系统。
用最初有限的基本几何不变量与一系列作图规则并且建立有限的一系列与这些不变量和作图规则有关的消点公式,把命题的前提以作图语句的形式输入,自动化程序就可以调用相应的消点公式把结论中的约束关系逐个消去,最后得出结论,把消点的过程记录起来并且与相应的消点公式结合,就是一个具有几何意义的证明过程。
可喜的是此法亦可由人用笔在纸上执行,我们称为的消点法,消点法把证明与作图联系起来,把代数演算与几何推理密切相联,从而几何解题的逻辑性增强了,把初等几何解题从只运用四则运算的层次推进到代数方法的阶段,几何证题亦有了以不变应万变的模式。
既然消点法是在面积法的基础上发展起来的,那么下面列出消点法要用到的公式定理:1、共边定理有一条公共边的两个三角形,叫做共边三角形。

消失点工具的使用原理
消失点工具是一种绘画辅助工具,它可以帮助艺术创作者正确绘制透视关系。
其原理如下:1. 透视原理透视绘画需要遵循物体前后远近与图像大小对应等原理。
2. 机械装置原理消失点工具包含移动笔杆、凸透镜等机械结构。
3. 虚像原理凸透镜可放大图像,通过放大虚像帮助观察准确位置。
4. 对准目标将工具调整对准绘画中的目标物体或线条。
5. 观察虚像从透镜观察目标的虚像,移动笔杆调整图片大小。
6. 标记消失点当虚像缩小至一点时,即为该目标在图片中的消失点。
7. 连接消失点用线条连接不同目标的消失点,绘制出透视关系。
8. 绘制透视根据连接的消失点绘制物体的透视关系。
9. 助理创作构图使用消失点绘制准确的透视构图,有助创作透视关系正确的艺术作品。
综上,消失点工具利用光学原理辅助绘制,是透视绘画的重要辅助工具,方便艺术创作者准确描绘物体的透视感。
初中数学如何使用消失点绘制透视图使用消失点绘制透视图是一种常用的方法,可以使绘制的图形更具立体感和逼真度。
下面将详细介绍如何使用消失点绘制透视图。
1. 确定视点和投影平面:首先,确定视点的位置和投影平面的选择。
视点是观察者所处的位置,一般位于透视图的上方,远离绘制的物体。
投影平面是物体在透视图上的投影所在的平面,与物体平行。
通过确定视点和投影平面,我们可以决定透视图的观察角度和投影方式。
2. 确定物体的结构和平行线的走向:在绘制透视图前,需要先了解物体的结构和平行线的走向。
平行线在透视图中会逐渐靠近,最终汇聚到消失点。
通过观察物体的结构和平行线的走向,我们可以推测出平行线在透视图中的方向,并由此确定消失点的位置。
3. 确定消失点的位置:根据物体的结构和平行线的走向,确定消失点的位置。
将平行线的延长线绘制到透视图上,并找到它们的交点,即为消失点的位置。
如果透视图中存在多组平行线,则需要找到每组平行线的消失点,并将它们标记在透视图上。
4. 绘制基本轮廓和线段:根据物体的形状和结构,在透视图上绘制物体的基本轮廓和线段。
通过参照物体的实际形状和尺寸,使用直线和曲线来绘制物体的轮廓和主要线段。
根据透视原理,注意线段的方向和长度,使其符合透视效果。
5. 运用消失点绘制透视效果:利用消失点来绘制透视效果。
通过观察物体的平行线和消失点的关系,绘制物体的细节和纹理,使其看起来更具立体感和逼真度。
例如,通过绘制平行线与消失点的交点,可以确定物体的边缘和表面的转折点。
6. 添加阴影和细节:根据光源的位置,添加阴影和细节,使透视图更加逼真。
根据光线的照射方向和物体的形状,用不同的灰度和明暗来描绘物体的阴影和高光。
通过绘制阴影和细节,可以增强透视图的立体感和深度感。
7. 修饰和润色:最后,对透视图进行修饰和润色,使其更加完善和吸引人。
可以运用色彩、纹理和细节来增加透视图的表现力和艺术性。
注意细节的准确性和透视效果的一致性,使透视图看起来更真实和生动。
消点法、添点法还原几何体的直观图作者:许苏华来源:《学习周报·教与学》2020年第12期摘 ;要:通过消点法和添点法,可以大大简化思维量,能够高效地把空间几何体的三视图方便地还原成直观图,使得问题迎刃而解。
关键词:消点法:添点法;空间几何体的直观图根据三视图求原空间几何体的表面积、体积、最长的棱长、直角三角形的个数、外接球的半径等,是高考数学常见题型之一,也是空间想象能力较弱的同学易做错的题型之一。
数学家张景中院士在他的面积法的基础上,发展出了消点法,并由此使得机器证明几何得以实现。
借鉴张院士的消点法思想,可以高效解决上述高考数学题型。
下面先以2018年北京理科卷第5题为例,介绍如何“消点”“添点”。
例1 (2018年北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()。
A.1 ; ;B. 2C. 3 ; ;D. 4解此题的关键是画出该四棱锥的直观图,困扰学生的问题一是如何画出?二是画出之后能否判断侧面是否是直角三角形?在该四棱锥的三视图中,没有任何曲线,都是直线型线段,我们可以根据该三视图中的长宽高,首先画一个完整的正方体ABCD-A1B1C1D1,如图1(1)所示。
根据题目所给的正(主)视图,消去点B1和C1,如图1(2)所示;根据侧(左)视图,消去点A1和B1,如图1(3)所示;根据俯视图,消去点B1和B,如图1(4)所示;再根据正(主)视图和俯视图添加一个点M(AB的中点),如图1(5)所示;最后把剩下的点D1、A、D、C和M,恰当地连接起来,构成的多面体就是原四棱锥,即四棱锥D1-AMCD,如图1(6)所示,由正方体的性质,很快判断出该四棱锥有三个侧面是直角三角形。
上述依次根据正(主)视图、侧(左)视图和俯视图,依次在补全的长方体(或正方体)直观图中,去掉不存在的点的方法,稱为消点法。
根据多个三视图,在长方体直观图中,添加点的方法,称为添点法。
这里的“消点法”,和张院士的“消点法”有所不同,详情见张院士的《几何新方法和新体系》一书。
运用消失点创造透视效果透视是绘画和摄影中常用的一种技巧,通过运用消失点可以创造出逼真的透视效果。
消失点是指在透视图中,所有平行线都会汇聚的点。
在绘画和摄影中,通过合理运用消失点,可以使画面更加立体、真实,给人以强烈的空间感和逼真的视觉效果。
本文将介绍如何运用消失点来创造透视效果。
一、消失点的概念和作用消失点是透视图中的一个重要概念,它是指在透视图中,所有平行线都会汇聚的点。
消失点的位置和数量取决于画面中的物体和透视角度。
在绘画和摄影中,通过合理运用消失点,可以使画面中的物体呈现出透视效果,增强画面的立体感和真实感。
消失点的作用主要有以下几个方面:1. 创造透视效果:通过将平行线引向消失点,可以使画面中的物体呈现出透视效果,增强画面的立体感。
2. 确定画面的空间结构:消失点的位置和数量可以帮助确定画面中物体的位置和大小,从而构建画面的空间结构。
3. 引导观众的视线:通过合理运用消失点,可以引导观众的视线,使其在画面中的物体之间产生流动感,增强画面的动态效果。
二、运用消失点创造透视效果的方法1. 确定透视角度:在绘画和摄影中,首先需要确定透视角度。
透视角度决定了消失点的位置和数量。
一般来说,透视角度越大,消失点越靠近画面中心;透视角度越小,消失点越靠近画面边缘。
2. 确定消失点的位置:根据透视角度,确定消失点的位置。
一般来说,消失点位于画面的水平线上,但也可以根据需要将其放置在其他位置。
3. 运用消失点绘制平行线:在绘画中,可以通过运用消失点来绘制平行线。
将平行线的两端连接到消失点,可以使平行线在远离观众的方向上逐渐收敛,从而创造出透视效果。
4. 运用消失点构建物体:在绘画和摄影中,可以通过运用消失点来构建物体。
将物体的边缘线连接到消失点,可以使物体在远离观众的方向上逐渐收敛,从而增强物体的立体感。
5. 运用消失点引导观众的视线:通过合理运用消失点,可以引导观众的视线,使其在画面中的物体之间产生流动感。
聆听院j
口中国科学院院士雅中
口华中师范大学教育信息技术工程研究中G彭翕成在上一期我们向大家介绍r消点法.井对消点法的应用举例进行说明.消点法是一个普遍有效的解题方法.消点法解题的要点如下:
(1)把题目中涉及的点按作图顺序排队.作阿过程中先出现的点排在前晰.后出现的点排在后面.
(2)把要解决的问题转化成对某个式子进行处理、化简的问题.
(3)从要化简的式子中,逐步消去由约束条件产生的点.后产生的先消去.
(4)消点时,一方而应用该点产生的几何条件,一方面对照图形.注意发现图形给我们提示的捷径.
掌握了I消点法之后.做几何题时.你便会胸有成竹r.你可以尝试着解下面这道胚:
倒如图l,在△A B C中,肋=2D C,A层=ED,
B F=3FE.已知s“F:12,求5“m.
解:首先利用兰竺!:旦:土消去点F:再利
S A^*B E4
用坠:丛里:土消去点E:最后利用鱼坐盟:丝4
SM∞A D2S_艇_B C
=三消去点D.这样.一个简洁的证明便产生r:
图1
因恙=瓮,卷.-卷=÷上生百1232,删s蒯.S△^时S^^艇S埘肌S△^毗4l一。
消点法虽然不能够解决所有几何问题,但我们ur以将它当饩解题的
归煎睦莹
指导方针.而且.我们还可以将消点法教给计算机.让计算机来帮助我们解题.这就是自动推理.
计算机是人的学生.它的本领是人教的.它是笨学生.不教不会;但它义是好学生。
会牢牢i c住你教给它的方法,一丝小苟地按写好的程序去做.盘¨聚你循循善诱.它又能青…于蓝而胜十蓝.计算机解题靠人教.人会解一道题.把方法教给计算机,汁算机就会解这道题.这道题中的数字换成字母.成r更一般化的·个题型.把处理这个题型的窍门教给计算机.计算机就会解这个题型的全部题.人掌握了·类题目的规律.把这规律总结提炼成有章可循的算法,实现为程序.计算机本领就会更大,会解这一类题了.人推演、计算、论证存易走神或出错.时州长了.所掌握的方法甚至有可能遗忘.但计算机一旦学会一套方法.就不会忘记.也很少卅错.J{且做题做得飞快!
几何题有汁算题、证明题.还有作图题.它们虽然各有特点,但义是相通的.
计算和作图都要有个道理.讲清楚道理就是让明.古希腊人研究几何最讲究证明.中国古代的几何学则讲究计算.把画图和推理都归结为计算,叫做寓理F算计算、作罔和证明,问题的形式不I i司.却也有相通之处.三类问题的前提.都可以用几何图形来表示.证明可以转化为汁算.要证明两条线段相等.H要算出两者的比为l或差为0就行了.要说明计算是准确的.作网过程是合理的.归根结底要证明.三类问题在解决过程中都要推演论证.推演论证所用的规则又是一致的.这就是一者的相通之处.
几千年来.人们解几何问题的招数层出不穷.争奇斗艳.概括起来,不外这四类:检验、搜索、约化和转换.近50多年来。
数学家和计算机科学家费尽心思.循循善诱.把个中奥秘向计算机传授.使得计算机解几何题的能力有了|长足的提高.除r灵机一动添加辅助线.或千变万化的问题转换之外.前j种招数计算机都学得十分出色r.用计算机帮助研究儿何.甚至代替老师指导学生学习几何,已经从古老的梦想变为了现实.许多几何问题包含了大量的信息.人在进行解题思考时能借助于直觉和经验.抓住最关键的信息进行解答;计算机却靠机械地搜索,大色小鱼一网打尽.工作量就非删小可r.譬如一个二角形和它的三条高以及
垂心.这是个很简单的几何图形.用计‘算机搜索几何信息.居然发现罔中有105组成比例的线段!
计算机在搜索中得到的有用信息很多。
但没用的信息更多.大量的操作才能从许多信息中寻找山有用的结论。
难度就好比沙里淘金.这种一网打尽、涸泽而渔的搜索式推理,并不是什么新的发明.而是一种古老的机械化推理设想.在没有计算机的时代,也只能想想而已.冈为_J二作量昕碗j
■丛生堑麴堂·蟹鱼厶麴畦垫塑E圆圈
手嚣,●
威功轴箍太大r.一旦有了计算机.科学家就希望将之付诸实践.现在.这个梦想已经成为现实.这个成功来之不易,是许多科学家多年努力的成果.其中,中国科学家的T作起了决定性的作用.而他们用到的“武器”,恰恰就是我们在前面连载文章中介纠的共边定理、共角定理,淌点法这些东西,你没有想到"巴1
学习需要对手
学习上.我觉得很重要的一点就是找到一个合适的对手.彳E 多时候“一枝独秀”并不是最理想的状态.没有竞争就没有进步,
如果一直处于无人撼动的地位。
就不会有前进的动力.所以,学
习上有一个与你旗鼓相当的对手是相当重要的.’我觉得自己很幸运.在高三学习中就有一个朋友,也是一个对手.这个朋友是我的同桌——解石坡.他人很聪明,知识很渊
博.学习上罪常刻苦.所以成绩一直很优秀I后来我们成了同桌,
就经常一起学习.现在看来.那时候我们既是朋友义是对手.我们
平时学习互相帮助,遇到不会做的难题就一起努力攻克,遇到不
开心的事也会讲出来让对方分担苦闷.
而每次考试时.我们便成了一对一的“死对头”.因为成绩都很优秀.学习水平基本上旗鼓相当,所以考试的时候就二f=:免较量
一番了。
在每次考试前.我们俩都会握手互相鼓励.我们都希望自
己能考好.但也会衷心地祝福对方.很有意思的是,每次班上考
试时.不是他第一就是我第一.我知道我们俩心中都憋着一股
劲.想超越对方.因为彼此离得很近,也很了解对方的情况,所以
我们会在平时的学习中时刻与对方比较,比如老师出的一道数
学题谁做得快啊.一道英语阅读题谁错得更少啊.这是一种有趣
的比较.但也真能促进我们俩很快地进步.因为不想被对方超
过.所以就要不停地努力.后来学校每次考试时,我们俩不但总
是分列第一和第二.而且考出的分数都会把其他人拉开一太截.如果没有他.我就不会有那么大的向前冲的动力.我想我们正是在与对方的一次次竞争中不断提高的.有一句话叫“人生得
一知已足矣”.我却想说“学习中得一‘对手’足矣”!
(甘肃省高考文科状元薛逢源)
磊可。