2.3从“买布问题”说起---一元一次方程的讨论(2

课题：2.3.3 从“买布问题”说起一元一次方程的讨论（2）教学目标1、会把实际问题建成数学模型，会用去分母的方法解一元一次方程．2、通过列方程解决实际问题，让学生逐步建立方程思想；通过去分母解方程，让学生了解数学中的“化归”思想．3、让学生了解数学的渊源及辉煌的历史，激发学生的学习热情教学难点实际问题中如何建立等量关系，并根据等量关系列出方程。

知识重点会用去分母的方法解一元一次方程教学过程（师生活动）设计理念引入1、引言：同学们，目前初中数学主要分成代数与几何两大部分，其中代数学的最大特点是引人了未知数，建立方程，对未知数加以运算．而最早提出这一思想并加以举例论述的，是古代数学名著《算术》一书，其作者是古希腊后期数学家—“代数学之父”丢番图．2、丢番图的墓志铭：“坟中安葬着丢番图，多么令人惊讶，它忠实地记录了所经历的道路．上帝给予的童年占六分之一又过十二分之一，两颊长胡．再过七分之一，点燃起结婚的蜡烛．五年之后天赐贵子，可怜迟到的宁馨儿，享年仅及其父之半，便进人冰冷的墓．悲伤只有用数论的研究去弥补，又过四年，他也走完了人生的旅途．”请你列出方程算一算，丢番图去世时的年龄？设丢番图去世时的年龄为x岁，由题意可列方程和以往不同的是，我们看到，上面这个方程中有些系数是分数，如果能化去分母，把系数化成整数，那么可以使解方程中的计算更方便一些。

去分母的关键在于：方程两边同时乘以各分母的最小公倍｝数84.于是，所列方程变为整系数方程，解得：x=84。

数学的历史是辉煌的，让学生了解数学的渊源，在历史的背景下进行数学的探求，有益于学生的数学学习。

试一试英国伦敦博物馆保存着一部极其珍贵的文物—纸莎草文书．现存世界上最古老的方程就出现在这部英国考古学家兰德1858年找到的纸草书上．经破译，上面都是一些方程，共85个问题．其中有如下一道著名的求未知数的问题：一个数，它的三分之二，它的一半，它的七分之一，它的全部，加起来总共是33，这个数为几何？探讨归纳解方程：1、为使方程变为整系数方程，方程两边应该同乘以什么数？2、在去分母的过程中，应该注意哪些易错的问题？3、解上述方程的全过程，展示了一元一次方程解法的一般步骤，试归纳、小结，并了解过程中每一步的主要依据．任何未知的探求都希望通过已知来解决，这是数学中“化归”思想的核心．问题的出现必须寻找以往的经验进行解决．于是，如何去分母成为主题．巩固练习1、完成课本90页练习。

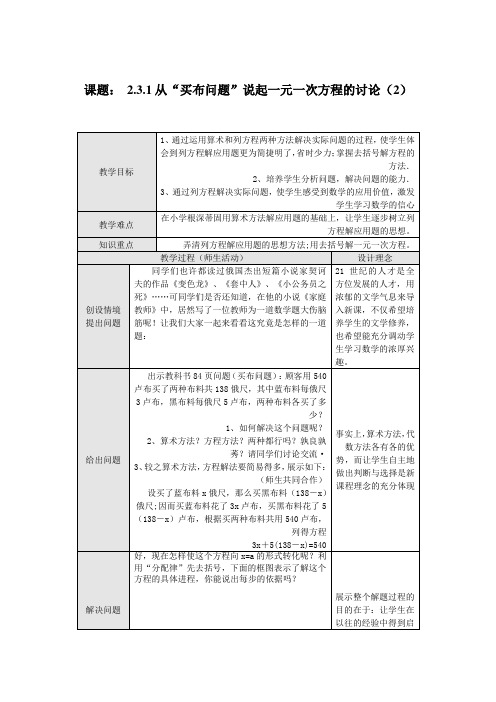
课题：2.3.1从“买布问题”说起一元一次方程的讨论（2）教学目标1、通过运用算术和列方程两种方法解决实际问题的过程，使学生体会到列方程解应用题更为简捷明了，省时少力；掌握去括号解方程的方法．2、培养学生分析问题，解决问题的能力．3、通过列方程解决实际问题，使学生感受到数学的应用价值，激发学生学习数学的信心教学难点在小学根深蒂固用算术方法解应用题的基础上，让学生逐步树立列方程解应用题的思想。

知识重点弄清列方程解应用题的思想方法;用去括号解一元一次方程。

教学过程（师生活动）设计理念创设情境提出问题同学们也许都读过俄国杰出短篇小说家契诃夫的作品《变色龙》、《套中人》、《小公务员之死》……可同学们是否还知道，在他的小说《家庭教师》中，居然写了一位教师为一道数学题大伤脑筋呢！让我们大家一起来看看这究竟是怎样的一道题：21世纪的人才是全方位发展的人才，用浓郁的文学气息来导入新课，不仅希望培养学生的文学修养，也希望能充分调动学生学习数学的浓厚兴趣。

给出问题出示教科书84页问题（买布问题）：顾客用540卢布买了两种布料共138俄尺，其中蓝布料每俄尺3卢布，黑布料每俄尺5卢布，两种布料各买了多少？1、如何解决这个问题呢？2、算术方法？方程方法？两种都行吗？孰良孰莠？请同学们讨论交流·3、较之算术方法，方程解法要简易得多，展示如下：（师生共同合作）设买了蓝布料x俄尺，那么买黑布料（138－x）俄尺;因而买蓝布料花了3x卢布，买黑布料花了5（138－x）卢布，根据买两种布料共用540卢布，列得方程3x＋5(138－x)=540事实上，算术方法，代数方法各有各的优势，而让学生自主地做出判断与选择是新课程理念的充分体现解决问题好，现在怎样使这个方程向x=a的形式转化呢？利用“分配律”先去括号，下面的框图表示了解这个方程的具体进程，你能说出每步的依据吗？展示整个解题过程的目的在于：让学生在以往的经验中得到启由上可知，买了75俄尺蓝布料和63俄尺黑布料。

2.3 从“买布问题〞说起——一元一次方程的讨论〔2〕5分钟训练 (预习类训练，可用于课前)1.一个饲养场里的鸡的只数与猪的头数之和是70，鸡、猪的腿数之和是196，设鸡有x只，依题意可列方程〔〕A.2x+4〔70－x〕=196B.2x+4×70=196C.4x+2〔70－x〕=196D.4x+2×70=196思路解析：每只鸡有2条腿，每头猪有4条腿，所以可列方程2x+4〔70-x〕=196.答案:A2.方程(m+1)x|m|+3=0是关于x的一元一次方程，那么m的值是〔〕A.±1B.1 C思路解析：方程(m+1)x|m|+3=0是关于x的一元一次方程，那么m+1≠0，|m|=1，所以m=1. 答案:B3.某校球类联赛期间买回排球和足球一共16个，花去900元钱.排球每个42元，足球每个80元，那么排球买了_________个.思路解析：假如设买回排球x个，那么足球个数为16-x，由此得方程42x+80(16-x)=900，解这个方程得x=10.答案:1010分钟训练(强化类训练，可用于课中)1.休斯敦HY队主力中锋姚明在对掘金队的一场比赛中，发挥特别出色，仅上半场就19投11中，另加罚篮10投8中，就拿下31分的高分.设他上半场投中2分球x次，那么可列方程〔〕A.2〔11－x〕+3x+8=31B.2x+3〔19－x〕+8=31C.2x+3〔11－x〕+8=31D.2x+3〔11－x〕+2×8=31思路解析：篮球投球得分有2分，3分两种，罚球投中1分，要注意干扰数19与10.答案:C2.解以下方程：〔1〕3〔4－2x〕=5x+23. 〔2〕4(2y+3)=8(1-y)-5(y-2).思路解析：先去括号，再移项，合并，最后把系数化为1.解：〔1〕去括号，得12-6x=5x+23..移项，得-6x-5x=23-12.合并，得-11x=11.解得x=-1. 〔2〕去括号，得8y+12=8-8y-5y+10.移项，得8y+8y+5y=8+10-12.合并，得21y=6.解得y=27.3.解以下方程：〔1〕13x--x=3-24x+；〔2〕23x-=32x-.思路解析：先乘分母的最小公倍数去分母，此时要注意不要遗漏单项式及常数项.再移项，合并，最后把系数化为1.解：〔1〕去分母，得4〔1-x〕-12x=36-3(x+2).去括号，得4-4x-12x=36-3x-6.移项，得-4x-12x+3x=36-6-4.合并，得-13x=26.系数化为1，得x=-2.〔2〕去分母，得2(x-2)=3(x-3).去括号，得2x-4=3x-9.移项，得2x-3x=-9+4.合并，得-x=-5.系数化为1，得x=5.4.解一元一次方程的一般步骤是：(填下表)答案:解一元一次方程的一般步骤：5.“希望工程〞是我们都关心的问题，许多团体和个人都为“希望工程〞捐款捐物，奉献自己的爱心.某文艺团体组织了一场募捐义演，成人票每张8元，学生票每张5元，一共售出1 000张，筹得票款6 950元.问成人票和学生票各售出多少张.思路解析：解应用题的关键是找出可以表示全部含义的等量关系，此题中有两个等量关系：成人票数+学生票数=1 000张；成人票款+学生票款=6 950元；可以利用其中任意一个等量关系设未知数，利用另一个等量关系列方程.解法一：设售出的学生票为x张，那么售出的成人票为1 000-x张.那么由题意有8〔1 000-x〕+5x=6 950，解得x=350.解法二：设售出的学生票为x张，那么售出的成人票为695058x-张.由于一共售出1 000张门票，那么有x+695058x-=1 000，解得x=350.答案：售出的学生票为350张，售出的成人票为650张.快乐光阴饭厅内，一个异常谦恭的人害怕地碰了碰另一个顾客，那人正在穿一件大衣.“对不起，请问您是不是皮埃尔先生？〞“不，我不是.〞那人答复，“啊，〞他舒了一口气.“那我没弄错，我就是他，您穿了他的大衣.〞30分钟训练(稳固类训练，可用于课后)1.以下方程变形正确的选项是〔〕①3x+6=0变形为x+2=0 ②x+7=5－3x变形为4x=－2③25x=3变形为2x=15 ④4x=－2变形为x=－2A.①③B.①②③C.③④D.①②④思路解析：注意去分母、去括号、移项、合并同类项、系数化为1几个步骤是否正确.①3x+6=0变形为x+2=0，是方程两边同除以3得的，正确；②x+7=5-3x变形为4x=-2，是把-3x移到等号的左边，把7移到等号的右边，合并同类项得到的，正确；③25x=3变形为2x=15，是方程两边同乘以5得的，正确；④4x=-2变形为x=-2，方程左边除以4，右边没有除，错误.所以答案为B.答案:B2.假设x－(5+2y)=15，那么2x－4y的值是〔〕A.20B.30 C思路解析：把x-(5+2y)=15的括号去掉，可得x-2y=20，再两边同乘以2,得2x-4y=40. 答案:C3.解方程：3(x+1)－(5+x)=18－2(x－1).思路解析：去括号时，注意括号前是负号的运算.解：去括号，得3x+3-5-x=18-2x+2.移项，得3x-x+2x=18+2-3+5.合并同类项，得4x=22.系数化为1，得x=11 2.4.解以下方程：〔1〕24x+－1=236x-；〔2〕13〔1－2x〕=27〔3x+1〕；〔3〕12［3x－15〔x+1〕］－1=x；〔4〕0.20.1320.36x x--- =1.解：〔1〕去分母，得3(x+2)-12=2(2x-3).去括号，得3x+6-12=4x-6.移项，得3x-4x=-6-6+12.合并同类项，得-x=0.系数化为1得x=0.〔2〕去分母，得7(1-2x)=6(3x+1).去括号，得7-14x=18x+6.移项，得-14x-18x=6-7.合并同类项，得-32x=-1.系数化为1得x=1 32.〔3〕左右两边乘2，得3x-15〔x+1〕-2=2x.去括号，得3x-15x-15-2=2x，移项，得3x-15x-2x=15+2.合并同类项，得45x=115.系数化为1，得x=114.〔4〕系数化为整数，得213236x x---=1.去分母，得2(2x-1)-(3x-2)=6.去括号，得4x-2-3x+2=6.移项，得4x-3x=6-2+2,系数化为1，得x=6.5. 关于x的方程ax-2=3(a+x)的根是2，求a的值.解：方程的根必须满足方程，那么可以将x=2代入原方程，建立关于a的方程，求解即可. 解：将x=2代入原方程，那么有2a-2=3(a+2)，解得a=-8.6.有甲、乙两种学生辅导用书，甲种书的单价是8元，乙种书的单价是9.5元，两种书一共卖了100本，卖了882.5元，两种书各卖出多少本？思路解析：此题有以下两种等量关系：卖出甲种书的本数+卖出乙种书的本数=100本；卖甲种书的钱数+卖乙种书的钱数=882.5元.可以由任意一个等量关系设未知数，另一个等量关系列方程.解：设甲种书卖出x本，那么乙种书卖出〔100-x〕本，由题意有8x+9.5(100-x)=882.5，解得x=45.所以甲种书卖出45本，乙种书卖出55本.答:甲种书卖出45本，乙种书卖出55本7.模拟小刚在商场发现他喜欢的随身听和书包单价之和是452元，并且随身听的单价比书包单价的4倍少8元.求小刚喜欢的随身听和书包的单价.思路解析：题中表示等量关系的语句是“随身听和书包单价之和是452元，并且随身听的单价比书包单价的4倍少8元〞.设随身听单价为x元，那么书包的单价为(452-x)元,这样可得方程x=4(452-x)-8，解出即可.解：设随身听单价为x元，那么书包的单价为(452-x)元,列方程，得x=4(452-x)-8.解得x=360.当x=360时，452-x=92.答:随身听单价为360元，书包单价为92元.8.模拟足球比赛的记分规那么为：胜一场得3分，平一场得1分，输一场得0分.一支足球队在某个赛季中一共需比赛14场,现已比赛了8场,输了1场,得17分.请问：(1)前8场比赛中,这支球队一共胜了多少场?(2)这支球队打满14场比赛,最高能得多少分?(3)通过比照赛情况的分析,这支球队打满14场比赛,得分不低于29分,就可以到达预期的目的.请你分析一下,在后面的6场比赛中,这支球队至少要胜几场,才能到达预期目的?思路解析：“现已比赛了8场,输了1场,得17分〞，即胜、平7场，设这个球队胜x场,那么平了(8-1-x)场，这样可得方程3x+(8-1-x)=17，解出即可.解：(1)设这个球队胜x场,那么平了(8-1-x)场.根据题意,得3x+(8-1-x)=17.解得x=5.答:前8场比赛中,这个球队一共胜了5场.(2)打满14场比赛最高能得17+(14-8)×3=35分.(3)由题意知,以后的6场比赛中,只要得分不低于12分即可.所以胜不少于4场,一定到达预期目的,而胜3场、平3场，正好到达预期目的.所以在以后的比赛中这个球队至少要胜3场.9.某公园的门票价格规定如下表所列.某初一(1)、(2)两个班一共104人去游园，其中(1)班人数较少，不到50人，(2)班人数较多，超过50人.经估算，假如两班都以班为单位分别购票，那么一一共应付1 240元；假如两班结合起来，作为一个团体购票，那么可以节不少钱.问两班各有多少名学生.思路解析：题中有这样一个关系：“假如两班都以班为单位分别购票，那么一一共应付1 240元〞.由此可得方程.解：设初一(1)班有x名学生，那么初一(2)班有(104-x)名学生，据题意有13x+11(104-x)=1 240；解方程得x=48.所以初一(2)班学生有104-x=104-48=56名.答:初一(1)班有48名学生，初一(2)班有56名学生.。