下载文档原格式
姓名: 学号: 得分:实验四 线性系统的根轨迹一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、基础知识及MATLAB 函数根轨迹是指系统的某一参数从零变到无穷大时，特征方程的根在s 平面上的变化轨迹。
这个参数一般选为开环系统的增益K 。
课本中介绍的手工绘制根轨迹的方法，只能绘制根轨迹草图。
而用MATLAB 可以方便地绘制精确的根轨迹图，并可观测参数变化对特征根位置的影响。
假设系统的对象模型可以表示为11210111()()m m m m n n n nb s b s b s b G s KG s K s a s b s a -+--++++==++++ 系统的闭环特征方程可以写成01()0KG s +=对每一个K 的取值，我们可以得到一组系统的闭环极点。
如果我们改变K 的数值，则可以得到一系列这样的极点集合。
若将这些K 的取值下得出的极点位置按照各个分支连接起来，则可以得到一些描述系统闭环位置的曲线，这些曲线又称为系统的根轨迹。
绘制系统的根轨迹rlocus （）MATLAB 中绘制根轨迹的函数调用格式为:rlocus(num,den) 开环增益k 的范围自动设定。
rlocus(num,den,k) 开环增益k 的范围人工设定。
rlocus(p,z) 依据开环零极点绘制根轨迹。
r=rlocus(num,den) 不作图，返回闭环根矩阵。
[r,k]=rlocus(num,den) 不作图，返回闭环根矩阵r 和对应的开环增益向量k 。
其中，num,den 分别为系统开环传递函数的分子、分母多项式系数，按s 的降幂排列。
K 为根轨迹增益，可设定增益范围。
例3-1:已知系统的开环传递函数32(1)()429s G s K s s s *+=+++，绘制系统的根轨迹的matlab 的调用语句如下:num=[1 1]; %定义分子多项式den=[1 4 2 9]; %定义分母多项式rlocus (num;den) %绘制系统的根轨迹grid %画网格标度线xlabel(‘Real Axis ’),ylabel(‘Imaginary Axis ’) %给坐标轴加上说明 title(‘Root Locus ’) %给图形加上标题名 则该系统的根轨迹如图3-1（a ）所示。
线性系统的根轨迹一、 实验目的1． 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2． 利用MATLAB 语句绘制系统的根轨迹。
3． 掌握用根轨迹分析系统性能的图解方法。
4． 掌握系统参数变化对特征根位置的影响。
二、 实验容1． 请绘制下面系统的根轨迹曲线。
)136)(22()(22++++=s s s s s K s G )10)(10012)(1()12()(2+++++=s s s s s K s G )11.0012.0)(10714.0()105.0()(2++++=s s s s K s G 同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的围。
2． 在系统设计工具rltool 界面中，通过添加零点和极点方法，试凑出上述系统，并观察增加极、零点对系统的影响。
三、 实验结果及分析1.（1） )136)(22()(22++++=s s s s s K s G 的根轨迹的绘制： MATLAB 语言程序：num=[1];den=[1 8 27 38 26 0];rlocus(num,den)[r,k]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis') title('Root Locus')运行结果：选定图中根轨迹与虚轴的交点，单击鼠标左键得：selected_point =0.0021 + 0.9627ik =28.7425r =-2.8199 + 2.1667i-2.8199 - 2.1667i-2.3313-0.0145 + 0.9873i结论：根轨迹与虚轴有交点，所以在K 从零到无穷变化时，系统的稳定性会发生变化。
由根轨迹图和运行结果知，当0<K<28.7425时，系统总是稳定的。
（2） )10)(10012)(1()12()(2+++++=s s s s s K s G 的根轨迹的绘制： MATLAB 语言程序：num=[1 12]；den=[1 23 242 1220 1000];rlocus(num,den)[k,r]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis')title('Root Locus')运行结果：选定图中根轨迹与虚轴的交点，单击鼠标左键得：selected_point =k =1.0652e+003r=-11.4165 + 2.9641i-11.4165 - 2.9641i-0.0835 + 9.9528i-0.0835 - 9.9528i结论：根轨迹与虚轴有交点，所以在K 从零到无穷变化时，系统的稳定性会发生变化。
线性系统的根轨迹法实验报告实验二线性系统的根轨迹法一,实验目的1，掌握matlab绘制根轨迹的方法。
2，观察k值变化对系统稳定性的影响。
3，掌握系统临界稳定情况下k值得求取。
4，了解增设零点对系统稳定的影响以及改善系统稳定性的方法。
二，实验原理根轨迹的概念:所谓根轨迹就是当开环系统某一参数从零变到无穷大时，闭环系统特征方程式的根在s平面上变化的轨迹。
根轨迹与系统性能:有了根轨迹就可以分析系统的各种性能了，稳定性的判定，当开环增益从零变到无穷大时，根轨迹不会越过虚轴进入s平面的右半平面，此时K的范围为系统稳定的范围，根轨迹与虚轴的交点处的K值，为系统的临界开环增益，开根轨迹进入s平面的右半平面时所对应的K值为系统不稳定的情况。
三，实验内容A、设单位负反馈系统的开环传递函数为G(s)=K/(s*(s+1)(s+5)) (1) 绘制系统的根轨迹，并将手工绘制结果与实验绘制结果比较; (2) 从实验结果上观察系统稳定的K 值范围;(3) 用simulink 环境观察系统临界稳定时的单位阶跃响应分析:绘制根轨迹的matlab文本为clfnum=1;den=conv([1 1 0],[1 5]); rlocus(num,den) %绘制系统根轨迹1,得到如图的根轨迹图:2,用鼠标点击根轨迹与虚轴处的交点可得到临界稳定的开环增益K=30,所以系统稳定的K值范围为0―30。
3，在simulink环境下按下图连接电路:取增益为30的时候在示波器下观察单位节约响应，输出波形为:由图可以看出单位阶跃响应的输出为等幅的震荡输出，所以此时系统为临界稳定状态。
当改变开环增益为50和20时观察示波器，得到输出波形分别为:由图可知当增益K为50时输出为不稳定的震荡输出，此时系统不稳定，当增益K为20时输出的波形震荡越来越缓慢，最后趋于稳定，所以此时的系统是稳定的。
B，设单位反馈控制系统的开环传递函数为G(S)=K(s+3)/s(s+1)(s+2)(1) 仿照上题绘制系统的根轨迹，并判断系统的稳定性; 参照第一题得到matlab命令文本为:clfnum=1;den=conv([1 1 0],[1 2]); rlocus(num,den) %绘制系统根轨迹得到如图的根轨迹图:1，由图可知根轨迹没有进入s平面右半平面，所以系统在K=0到K=?都是稳定的。
线性系统的根轨迹及频域分析实验一、实验目的1、学习使用MATLAB软件仿真，掌握根轨迹及频域分析的方法。
2、熟悉并掌握运用根轨迹法分析线性系统增加开环零极点对系统性能的影响。
3、熟悉并掌握运用频域法分析线性系统调整系统典型环节的组成对系统性能的影响。
4、掌握从两个不同分析角度对同一系统进行分析的方法。
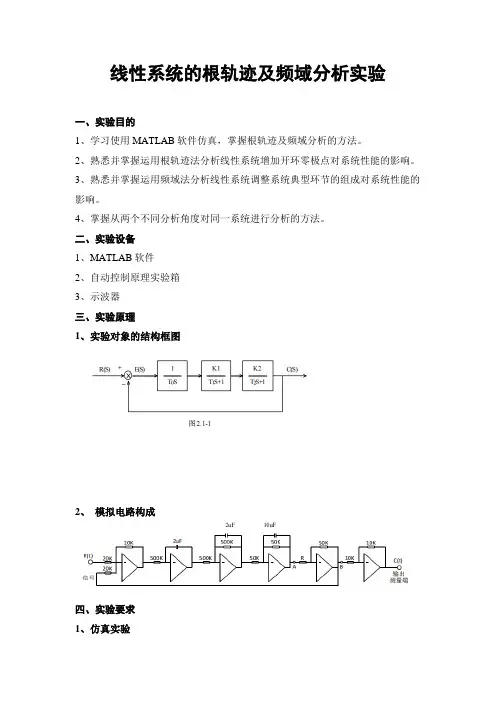
二、实验设备1、MATLAB软件2、自动控制原理实验箱3、示波器三、实验原理1、实验对象的结构框图2、模拟电路构成四、实验要求1、仿真实验（1）按照第二部分仿真作业4、5的要求，完成仿真测试，记录并分析仿真波形。
（2）根据传递函数绘制其根轨迹。
并选取适当的K值，分别使系统处于不稳定、临界稳定和稳定状态时，输出系统的时域曲线和伯德图，并对输出曲线进行分析。
（3）对系统分别增加不同位置的零极点，观察零极点对系统性能的影响五、实验步骤1、绘制根轨迹图：根据对象传递函数用仿真软件画出对象的根轨迹图，对其稳定性及暂态性能做出理论上的判断。
2、在根轨迹上取三个点，分别位于系统不稳定、临界稳定、稳定范围内，求其对应的K值分别为K1、K2、K3。
3、绘制参数分别为K1、K2、K3时系统的时域响应曲线（matlab命令用step()函数实现）和伯德图（matlab命令用bode()函数实现）。
4、给原系统增加一个开环零点，该零点分别设置为位于虚轴右侧、位于所有开环极点左侧以及位于某两个开环极点之间三种情况，记录并分析增加开环零点后的系统根轨迹曲线。
5、给原系统增加一个开环极点，该极点分别设置为位于虚轴右侧、位于所有开环极点左侧以及位于某两个开环极点之间三种情况，记录并分析增加开环零点后的系统根轨迹曲线。
六、实验数据、波形及分析1、记录并分析系统开环传递函数为的时域响应曲线和伯德图。
（1）分别绘制增益K 取K1、K2、K3 时的时域响应曲线；（2）分别绘制增益K 取K1、K2、K3 时的伯德图；3、绘制增加开环零点后的系统根轨迹曲线。
姓名: 学号: 得分:实验四 线性系统的根轨迹一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、基础知识及MATLAB 函数根轨迹是指系统的某一参数从零变到无穷大时，特征方程的根在s 平面上的变化轨迹。
这个参数一般选为开环系统的增益K 。
课本中介绍的手工绘制根轨迹的方法，只能绘制根轨迹草图。
而用MATLAB 可以方便地绘制精确的根轨迹图，并可观测参数变化对特征根位置的影响。
假设系统的对象模型可以表示为11210111()()m m m m n n n nb s b s b s b G s KG s K s a s b s a -+--++++==++++系统的闭环特征方程可以写成01()0KG s +=对每一个K 的取值，我们可以得到一组系统的闭环极点。
如果我们改变K 的数值，则可以得到一系列这样的极点集合。
若将这些K 的取值下得出的极点位置按照各个分支连接起来，则可以得到一些描述系统闭环位置的曲线，这些曲线又称为系统的根轨迹。
绘制系统的根轨迹rlocus （）MATLAB 中绘制根轨迹的函数调用格式为:rlocus(num,den) 开环增益k 的范围自动设定。
rlocus(num,den,k) 开环增益k 的范围人工设定。
rlocus(p,z) 依据开环零极点绘制根轨迹。
r=rlocus(num,den) 不作图，返回闭环根矩阵。
[r,k]=rlocus(num,den) 不作图，返回闭环根矩阵r 和对应的开环增益向量k 。
其中，num,den 分别为系统开环传递函数的分子、分母多项式系数，按s 的降幂排列。
K 为根轨迹增益，可设定增益范围。
例3-1:已知系统的开环传递函数32(1)()429s G s K s s s *+=+++，绘制系统的根轨迹的matlab的调用语句如下:num=[1 1]; %定义分子多项式 den=[1 4 2 9]; %定义分母多项式 rlocus (num;den) %绘制系统的根轨迹 grid %画网格标度线xlabel(‘Real Axis ’),ylabel(‘Imaginary Axis ’) %给坐标轴加上说明 title(‘Root Locus ’) %给图形加上标题名 则该系统的根轨迹如图3-1（a ）所示。
若上例要绘制K 在（1，10）的根轨迹图，则此时的matlab 的调用格式如下，对应的根轨迹如图3-1（b ）所示。
num=[1 1]; den=[1 4 2 9];k=1:0.5:10;rlocus (num;den;k)1）确定闭环根位置对应增益值K 的函数rlocfind （）在MATLAB 中，提供了rlocfind 函数获取与特定的复根对应的增益K 的值。
在求出的根轨迹图上，可确定选定点的增益值K 和闭环根r （向量）的值。
该函数的调用格式为:[k,r]=rlocfind(num,den)执行前，先执行绘制根轨迹命令rlocus （num,den ），作出根轨迹图。
执行rlocfind 命令时，出现提示语句“Select a point in the graphics window ”，即要求在根轨迹图上选定闭环极点。
将鼠标移至根轨迹图选定的位置，单击左键确定，根轨迹图上出现“+”标记，即得到了该点的增益K 和闭环根r 的返回变量值。
例3-2:系统的开环传递函数为23256()8325s s G s K s s s *++=+++，试求:（1）系统的根轨迹；（2）系统稳定的K 的范围；（3）K=1时闭环系统阶跃响应曲线。
则此时的matlab 的调用格式为:G=tf([1,5,6];[1,8,3,25]);rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G ,1); %形成单位负反馈闭环系统step(G_c) %绘制闭环系统的阶跃响应曲线则系统的根轨迹图和闭环系统阶跃响应曲线如图3-2所示。
其中，调用rlocfind （）函数，求出系统与虚轴交点的K 值，可得与虚轴交点的K 值为0.0264，故系统稳定的K 的范围为(0.0264,)K ∈∞。
（a ） 完整根轨迹图形 （b ）特定增益范围内的根轨迹图形图3-1 系统的根轨迹图形（a ）根轨迹图形 （b ）K=1时的阶跃响应曲线图3-2 系统的根轨迹和阶跃响应曲线三、实验内容1．请绘制下面系统的根轨迹曲线22()(22)(613)KG s s s s s s =++++2(12)()(1)(12100)(10)K s G s s s s s +=++++2(0.051)()(0.07141)(0.0120.11)K G s s s s s +=+++同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围。
四、实验报告1．根据内容要求，写出调试好的MATLAB 语言程序，及对应的结果。
2. 记录显示的根轨迹图形，根据实验结果分析根轨迹的绘制规则。
3. 根据实验结果分析闭环系统的性能，观察根轨迹上一些特殊点对应的K 值，确定闭环系统稳定的范围。
4．写出实验的心得与体会。
五、预习要求1. 预习实验中的基础知识，运行编制好的MATLAB 语句，熟悉根轨迹的绘制函数rlocus()及分析函数rlocfind(),sgrid()。
2. 掌握用根轨迹分析系统性能的图解方法，思考当系统参数K 变化时，对系统稳定性的影响。
四：1. 22()(22)(613)KG s s s s s s =++++（1）程序代码：G=tf([1],[1,8,27,38,26]); rlocus (G); [k,r]=rlocfind(G)G_c=feedback(G,1); step(G_c)（2）实验结果：-8-6-4-22468Root LocusReal AxisI m a g i n a r y A x i sselected_point = -8.8815 + 9.4658i k =1.8560e+04 r =-10.2089 + 8.3108i -10.2089 - 8.3108i 6.2089 + 8.2888i 6.2089 - 8.2888iselected_point = -9.5640 - 7.6273i k =1.3262e+04 r =-9.5400 + 7.6518i -9.5400 - 7.6518i 5.5400 + 7.6258i 5.5400 - 7.6258iselected_point =-0.8436 + 1.1180ik =3.6752r =-3.1044 + 2.0194i-3.1044 - 2.0194i-0.8956 + 1.1669i-0.8956 - 1.1669iselected_point =-0.0095 + 2.1118ik =73.9872r =-3.9617 + 2.4724i-3.9617 - 2.4724i-0.0383 + 2.1409i-0.0383 - 2.1409i（3）结果分析：根轨迹与虚轴有交点，所以在K从零到无穷变化时，系统的稳定性会发生变化。
由根轨迹图和运行结果知，当0<K<73.9872时，系统总是稳定的。
2(12)()(1)(12100)(10)K s G s s s s s +=++++（1）程序代码：G=tf([1,12],[1,23,242,1220,1000]); rlocus (G);[k,r]=rlocfind(G) G_c=feedback(G,1); step(G_c) （2）实验结果：selected_point = -11.9076 + 2.6398i k =1.3433e+03 r =0.4698 +10.6207i 0.4698 -10.6207i -11.9698 + 2.8634i -11.9698 - 2.8634iselected_point = 0.0355 + 9.7826i k =1.0505e+03 r =-11.3838 + 2.9674i -11.3838 - 2.9674i -0.1162 + 9.9146i -0.1162 - 9.9146i（3）结果分析：根轨迹与虚轴有交点，所以在K 从零到无穷变化时，系统的稳定性会发生变化。
由根轨迹图和运行结果知，当0<K<1050.5时，系统总是稳定的。
2(0.051)()(0.07141)(0.0120.11)K G s s s s s +=+++（1） 程序代码：G=tf([0.05,1],[0.0008568,0.01914,0.1714,1,0]); rlocus (G);[k,r]=rlocfind(G)G_c=feedback(G,1);step(G_c)（2）实验结果：selected_point =-27.6540 + 0.1863ik =521.8293r =13.9393 +27.9598i13.9393 -27.9598i-27.6515-22.5660selected_point =0.0711 + 8.3851ik =7.8321r =-0.0336 + 8.5173i-0.0336 - 8.5173i-11.1359 + 1.4131i-11.1359 - 1.4131i（3）结果分析：根轨迹与虚轴有交点，所以在K从零到无穷变化时，系统的稳定性会发生变化。
由根轨迹图和运行结果知，当0<K<7.832时，系统总是稳定的.2.由以上根轨迹图知，根轨迹起于开环极点，终于开环零点。
在复平面上标出系统的开环零极点后,可以根据其零极点数之和是否为奇数确定其在实轴上的分布。
根轨迹的分支数等于开环传递函数分子分母中的最高阶次,根轨迹在复平面上是连续且关于实轴对称的。
当开环传递函数的分子阶次高于分母阶次时,根轨迹有n-m条沿着其渐近线趋于无穷远处。
根轨迹位于实轴上两个相邻的开环极点或者相邻零点之间存在分离点,两条根轨迹分支在复平面上相遇在分离点以某一分离角分开,不在实轴上的部分,根轨迹以起始角离开开环复极点,以终止角进入开环复零点。
有的根轨迹随着K的变化会与虚轴有交点。
在画图时,确定了以上的各个参数或者特殊点后,就可得系统的根轨迹概略图。
4. 本次实验我们首先熟悉了MATLAB用于控制系统中的一些基本编程语句和格式，随后又利用MATLAB语句绘制系统的根轨迹。
课本中介绍的手工绘制根轨迹的方法，只能绘制根轨迹草图，而用MATLAB可以方便地绘制精确的根轨迹图，并可通过自己添加零极点或者改变根轨迹增益的范围来观测参数变化对特征根位置的影响。
