第三节(泰勒级数展开)

高中数学泰勒展开公式高中数学中，泰勒展开公式是一种重要的数学工具，广泛应用于函数近似、求极限、研究函数性质等方面。

它由苏格兰数学家James Gregory和Brook Taylor在17世纪中期独立发现和证明，后来被统称为泰勒展开公式。

泰勒展开公式的基本思想是，将一个函数在某一点的邻域内用无穷级数的形式表示出来。

具体而言，对于任意光滑的函数f(x)，如果f(x)在x=a处有n阶导数，那么在x=a附近的某个区间内，f(x)可以用泰勒级数展开表示为：f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + ... +f^n(a)(x-a)^n/n!其中，f'(a)表示f(x)在x=a处的一阶导数，f''(a)表示f(x)在x=a处的二阶导数，f^n(a)表示f(x)在x=a处的n阶导数。

泰勒展开公式的一个重要应用是近似计算。

根据此公式，我们可以用高阶导数来逼近一个函数在某一点的近似值。

例如，当x离a较近时，我们可以截取泰勒级数展开的前几项来近似计算f(x)的值。

这在实际问题中具有重要意义，因为有时候我们无法直接求得一个函数在某一点的精确值，但可以通过泰勒级数展开来得到一个近似值。

泰勒展开公式还可以用于研究函数的性质。

例如，根据泰勒展开公式，我们可以判断一个函数在某一点的极限值。

通过对函数进行泰勒级数展开，我们可以分析函数在该点附近的行为，从而得到极限的性质。

这在高等数学中的微积分课程中是一个重要的应用。

总的来说，泰勒展开公式是高中数学中的一个重要工具，它在近似计算和函数性质研究中具有广泛应用。

掌握泰勒展开公式的使用方法，有助于学生更好地理解和应用数学知识，提高数学问题的解决能力。

泰勒展开定理的内容泰勒展开定理（Taylor Series Theorem）是一类由英国数学家泰勒于1797年研究发明的函数展开定理。

它把一类可展开的复杂函数通过不断地展开若干次，用更加简单的函数近似表示出来，其代表展开式也被成为泰勒级数展开式。

泰勒展开定理的基本内容是：任意在某一闭区间[a,b]内可连续展开的函数f(x)，可用其在某一点x=x0近似的泰勒级数展开式，来表示它在该闭区间所有点的值。

由此可知，泰勒级数展开式是一种形式比较复杂的函数近似展开系数表示法，通过高次（指定次数）的展开矩阵，将不可分拆解的函数表示成可以计算机求解的一系列多项式形式组合。

一般来说，泰勒级数展开式可以把一个函数看成是多项式函数的一个近似，用它表示某一函数f(x)，可用形式：f(x)=a_0 + a_1(x-x_0) + a_2(x-x_0)^2 +…+ a_n(x-x_0)^n+…式中x=x_0是近似点，a_i（i=0,1,2,3…）是系数，n为次数，满足微元积分解：a_n=1/n! * (f^(n))(x_0)其中(f^(n))(x_0)表示函数f(x)的n次导数在点x_0的值。

若在区间（a,b）上对函数f(x)展开，即x_0在区间（a,b）上，将在此区间内的任意可展开的函数投影到一条n次多项式上，此时将分别用适当的系数替代a_i中的系数，则可得到此区间特定的多项式表示。

这一定理有一定的几何意义，即是椭圆函数的展开式。

因为椭圆函数也是连续可导的函数，这意味着它可以经过泰勒级数展开来表示它的曲线，即：当x_1在[a,b]区间内任取一点时，函数f(x)展开后的多项式就是椭圆的曲线，那么在x_1点处，曲线就是最接近函数f(x)的。

总之，泰勒展开定理是将复杂函数通过多项式拆分为一系列多项式函数，可以在一定范围内准确地近似表示可展开函数f(x)，具有重要的应用价值。

泰勒展开常用公式泰勒展开公式（Taylor expansion formula）是一种用多项式函数来表示或近似另一直函数的数学方法。

它在数学、工程、物理、化学等多个领域具有广泛的应用。

泰勒展开公式以其便捷、高效的计算方式，成为数学领域中不可或缺的一部分。

泰勒展开公式适用于各种应用场景，例如在数值分析中用于求解非线性方程，在工程领域中用于近似计算复杂系统的特性，以及在科学研究中用于研究非线性现象等。

通过泰勒展开公式，我们可以将复杂的函数简化为一组多项式，便于进行计算和分析。

泰勒展开公式的计算步骤主要包括以下几个方面：1.确定展开项数：根据所需精度，确定展开项数。

2.计算各项系数：根据原函数的导数，计算泰勒展开公式中各项的系数。

3.展开计算：将原函数按照泰勒级数展开，得到多项式函数。

4.求解多项式方程：将展开后的多项式函数设为零，求解得到近似解。

泰勒展开公式在各领域都有显著的实例。

例如，在物理学中，可以用泰勒展开公式来描述电磁场的分布；在化学中，可以用泰勒展开公式来计算分子轨道的能量；在工程学中，可以用泰勒展开公式来近似计算非线性系统的稳定性。

泰勒展开公式与其他数学公式密切相关，如麦克劳林展开公式、傅里叶级数等。

这些公式都可以将复杂的函数转化为更容易处理的形式。

在我国，泰勒展开公式的研究历史悠久，众多学者对其进行了广泛深入的研究，取得了丰硕的成果。

泰勒展开公式在未来发展趋势中，将继续在各个领域发挥重要作用。

随着科技的发展，对泰勒展开公式的研究将更加深入，应用范围也将不断扩大。

在实际生活中，泰勒展开公式将有助于解决更多实际问题，提高人们的生活质量。

总之，泰勒展开公式作为一种重要的数学方法，在各个领域具有广泛的应用。

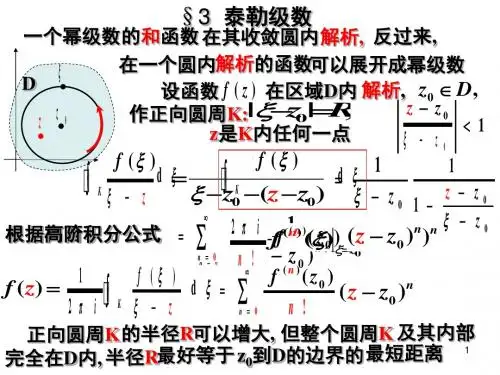
泰勒级数范围摘要：1.泰勒级数的概念和定义2.泰勒级数的展开形式3.泰勒级数的收敛区间4.泰勒级数的应用正文：1.泰勒级数的概念和定义泰勒级数，以英国数学家布鲁克·泰勒（Brook Taylor）的名字命名，是一种用多项式逼近函数的方法。

泰勒级数可以将函数在某一点附近的近似值表示为一个无穷级数。

具体来说，如果一个函数f(x) 在点a 附近可导，那么在a 点附近就可以展开一个泰勒级数。

2.泰勒级数的展开形式泰勒级数的展开形式如下：f(x) ≈ f(a) + f"(a)(x-a) + f""(a)(x-a)^2 / 2! + f"""(a)(x-a)^3 / 3! +...+ f^n(a)(x-a)^n / n! + Rn(x)其中，f"(a)、f""(a)、f"""(a) 等表示函数f(x) 在点a 处的各阶导数值，n! 表示n 的阶乘，Rn(x) 表示泰勒级数的余项。

3.泰勒级数的收敛区间泰勒级数的收敛区间取决于多项式的项数n 和函数f(x) 在展开点a 附近的性质。

当n 趋近于无穷大时，泰勒级数在a 点附近通常是收敛的，即泰勒级数的各项和可以无限接近函数f(x) 的真实值。

然而，在某些特殊情况下，如函数在展开点a 处具有奇点，泰勒级数可能发散。

4.泰勒级数的应用泰勒级数在数学和物理学等领域具有广泛的应用。

以下是一些常见的应用场景：- 求解函数的近似值：通过泰勒级数展开，可以在不需要计算函数原函数的情况下，快速得到函数在某一点附近的近似值。

- 求解微分方程的解：泰勒级数可以用于求解某些微分方程的解，例如常微分方程的线性近似解。

- 函数的逼近：泰勒级数可以用于逼近复杂的函数，例如在数值分析中，用泰勒级数逼近非线性函数以实现求解。

山东教育学院物理科学与技术系《数学物理方法》教学大纲一、课程概述1、《数学物理方法》是物理学专业本科的一门重要的基础课，它是前导课程《高等数学》的延伸，为后继开设的《电动力学》、《量子力学》以及《电子技术》等课程提供必需的数学理论知识和计算工具。

本课程在本科物理学专业中占有重要的地位，本专业学生必须掌握它们的基本内容，否则对后继课的学习将会带来很大困难。

在物理学专业的所有课程中，本课程是相对难学的一门课，学生应以认真的态度来学好本课程。

2、本课程的主要内容包括复变函数、傅立叶变换、数学物理方程、特殊函数等。

理论力学中常用的变分法，量子力学中用到的群论以及现代物理中用到的非线性微分方程理论等，虽然也属于《数学物理方法》的内容，但在本大纲中不作要求。

可以在后续的选修课中加以介绍。

3、本课程的内容为数学课程，注重逻辑推理和具有一定的系统性和严谨性。

但是，它与其它的数学课有所不同。

本课程内容有深广的物理背景，实用性强。

因此，在这门课的教学过程中，不能单纯地追求理论上的完美、严谨，而忽视其应用。

学生在学习时，不必过分地追求一些定理的严格证明、复杂公式的精确推导，更不能死记硬背，而应重视其应用技巧和处理方法。

4、本课程的内容是几代数学家与物理学家进行长期创造性研究的成果，几乎处处都闪耀创新精神的光芒。

教师应当提示学生注意在概念建立、定理提出的过程中所用的创新思维方法，在课堂教学中应尽可能地体现历史上的创造过程，提高学生的创造性思维能力。

二、目的要求1、为了使学生能学好物理学专业的理论物理课程， 胜任中学物理教学及适应社会主义现代化建设的需要， 在本门课程中系统讲授复变函数和数学物理方程的基本理论和基本方法，并介绍数学物理中常用的几种特殊函数。

要求学生对规定的内容有一个总体了解。

掌握其中的基本概念，熟悉一些重要的理论及公式，并使所学到的知识在头脑中形成合理的结构。

2、大纲贯彻少而精的原则，着重让学生掌握最基本的理论知识和计算方法.在讲授过程中紧密联系物理实际， 但也注意保证数学概念的严格性和理论的系统性。