北师大六年级上1.1圆的认识(一)(2)练习题及答案

【考点精讲+期中期末通用讲义—北师大版】六年级上册数学单元考点精讲+优选易错题（拔高版）01 圆一、圆的认识(一)1.圆的特征:由一条曲线围成的封闭图形，圆上任意一点到圆心的距离都相等。

在食指绕拇指旋转一周的过程中，拇指所按的点不变，食指与拇指间的距离不变。

2.圆的画法。

(1)手指画圆法。

以拇指为固定点，食指与拇指间的距离不变，将食指绕拇指旋转一周，食指的运动轨迹就形成了一个圆。

(2)实物画圆法。

把圆形物体放在纸上固定不动，用笔沿实物的边缘描一周，就画成了一个圆。

(3)系绳画圆法。

用一个图钉、一根线(没有弹力)和一支笔画圆的方法:用图钉将线的一端固定在一点上，用笔将线拉直并绕这个固定的点旋转一周，就画成了一个圆。

用图钉、线和笔画圆时，图钉要固定好，线要拉直。

(4)圆规画圆法。

根据圆心到圆上任意一点的距离(即半径)都相等，可以用圆规来画圆。

步骤如下:①把圆规的两脚分开，定好两脚间的距离(即半径);②把带有针尖的一只脚固定在一点(即圆心)上;③把带有铅笔的一只脚绕这个固定点旋转一周，就可以画出一个圆。

用圆规画圆，针尖所在的位置是圆心，两脚间的距离是半径。

3.圆的各部分名称。

(1)圆心。

画圆时，圆规带有针尖的脚所在的点叫圆心。

圆心一般用字母O表示。

(2)半径。

用圆规画圆时，圆规两脚之间的距离就是所画圆的半径，即圆心到圆上任意一点的距离叫半径。

半径一般用字母r表示。

在同一个圆里，所有半径的长度都相等。

1.同一个圆里有无数条半径，长度都相等。

2.直径是圆内最长的线段。

(3)直径。

通过圆心并且两端都在圆上的线段叫作直径。

直径一般用字母d表示。

在同一个圆里，所有直径的长度都相等。

4.圆的各部分之间的关系。

圆有无数条直径，无数条半径;同圆(或等圆)中的直径都相等，半径都相等;直径的长度是半径的2倍，可以表示为d=2r或r=d2。

5.圆心和半径的作用:圆心确定圆的位置，半径决定圆的大小。

6.圆在生活中的应用。

汽车车轮、自行车的车轮、球、齿轮、方向盘、圆规、井盖、钟表、水杯、环岛……1.判断直径和半径时，一定要看其是否经过圆心。

《圆的认识（一）》同步练习一、选择1. 用圆规画圆，圆规两脚的距离就是所画圆的( )A、圆心B、半径C、直径2. 圆中两端都在圆上的线段( )A、一定是圆的半径B、一定是圆的直径C、无法确定3. 在日常生活中，我们所见的下水井盖一般都制成( )。

A、正方形B、长方形C、圆形4.在同一个圆中最长的一条线段是( )。

A、半径B、直径C、直线5.画一个直径为5厘米的圆，圆规两脚之间的距离是( )A、5厘米B、10厘米C、2.5厘米二、判断并改错。

1、所有的半径都相等。

……………………………………………………（）2、直径的长度总是半径的2倍。

…………………………………………（）3、圆心决定圆的位置，半径决定圆的大小。

……………………………（）4、两端在圆上的线段是直径。

……………………………………………（）5、直径5厘米的圆与半径3厘米的圆大。

………………………………（）6、要画直径2厘米的圆，圆规两脚之间的距离就是2厘米。

…………（）7、圆有4条直径。

…………………………………………………………（）三、填一填1.圆心决定了圆的( ),半径决定了圆的( ).2.同一个圆中直径都()．半径都()3.连接()和()任意一点的线段叫半径.4.圆的直径通常用字母()表示,圆的半径通常用字母( )表示.5.圆规两脚间的距离为8厘米时,画出的圆的半径是()厘米．四、填表五、按要求画圆1.半径是1.5厘米。

2.直径是5厘米。

参考答案一、选择题1.B解析：画圆时圆规两脚间距离即半径。

2．C解析：两个端点都在圆上的线段肯定不是半径,有可能是直径,也可能不是。

3.C解析：生活中常见物体,一般为圆形。

4.C解析：同一个圆中线段最长。

5.C圆规两脚间距离是半径，r=5÷2 =2.5cm二、判断题1.错。

解析：大小不同的圆，直径和半径不相等。

2.错。

解析：同一个圆中直径是半径的2倍。

3.对。

解析：半径决定圆的大小,圆心决定圆的位置。

六年级上册数学一课一练-1.1圆的认识（一）一、单选题1.在一个边长6厘米的正方形内，能画出的圆的直径最大是（）。

A. 12厘米B. 3厘米C. 6厘米2.钟面上，分针和时针的针尖走过的轨迹都是一个圆，而且这两个圆（)。

A. 周长相等B. 是同心圆C. 是同一个圆D. 面积相等3.在一个长4cm、宽3cm的长方形中，画一个最大的圆，这个圆的直径是（）A. 3cmB. 4cmC. 14cm4.通过圆心并且两端都在圆上的（）叫做圆的直径．A. 射线B. 线段C. 直线二、判断题5.判断对错.通过圆心，并且两端都在圆上的线段叫做直径.6.判断．所有的圆的直径都相等．7.两段都在圆上并且经过圆心的线段是直径。

8.大圆的圆周率大于小圆的圆周率.三、填空题9.圆是轴对称图形，任何一条直径所在的直线都是圆的________。

10.画一半径为3厘米的圆，圆规两脚间应叉开________厘米．11.在一个半径为3厘米的圆内所有线段中，最长的一条是________厘米。

12.填空题（1）圆的直径是________．（2）圆的半径是________．四、解答题13.以点O为圆心，画一个直径为3厘米的圆．14.一个圆的直径是15.6米，它的半径是多少？五、综合题15.看图填空。

（1）d=________cmr=________cm（2）d=________cmr=________cm（3）d=________cmr=________cm六、应用题16.下图(单位：厘米)中，长方形的周长和面积各是多少？参考答案一、单选题1.【答案】C【解析】【解答】在一个边长6厘米的正方形内，能画出的圆的直径最大是6厘米.故答案为：C.【分析】在一个正方形内画最大的圆，这个圆的直径就是正方形的边长，据此解答.2.【答案】B【解析】【解答】钟面上，分针和时针的针尖走过的轨迹都是一个圆，而且这两个圆是同心圆.故答案为：B.【分析】根据对钟面的认识可知，在钟面上，分针和时针的针尖走过的轨迹都是一个圆，时针和分针是圆的半径，而且这两个圆是同心圆，据此解答.3.【答案】A【解析】【解答】解：在一个长4cm、宽3cm的长方形中画一个最大的圆，这个圆的直径就是宽的长度，是3厘米；如右图：故选：A．【分析】在这个长方形纸上画的最大圆的直径应等于长方形的宽，据此解答．解答此题的关键是明白：在这个长方形纸上画的最大圆的直径应等于长方形的宽．4.【答案】B【解析】【解答】解：通过圆心，并且两端都在圆上的线段叫做圆的直径；故选：B．【分析】根据直径的含义：通过圆心，并且两端都在圆上的线段叫做直径；进行解答即可．此题主要考查了圆的直径的含义，应注意基础知识的积累．二、判断题5.【答案】正确【解析】6.【答案】错误【解析】【解答】解：在同圆或等圆中，所有的直径都相等；故答案为：错误.【分析】解答此题应明确：所有的半径都相等，所有的直径都相等的前提条件是“在同圆或等圆中”．7.【答案】正确【解析】【解答】通过圆心且两个端点都在圆上的线段叫做圆的直径，由此可知题干所述正确故答案为：正确【分析】直径的两个端点均在圆周上，且这条线段过圆心，由此可得出答案。

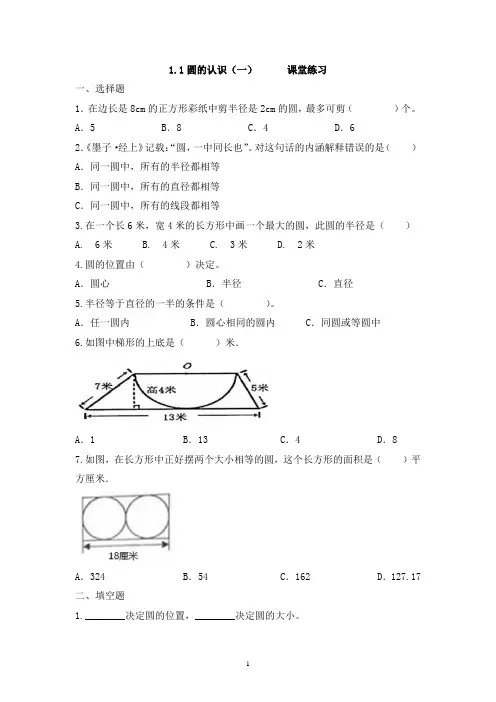
1.1圆的认识（一）课堂练习一、选择题1．在边长是8cm的正方形彩纸中剪半径是2cm的圆，最多可剪（）个。

A．5 B．8 C．4 D．62．《墨子·经上》记载：“圆，一中同长也”。

对这句话的内涵解释错误的是（）A．同一圆中，所有的半径都相等B．同一圆中，所有的直径都相等C．同一圆中，所有的线段都相等3.在一个长6米，宽4米的长方形中画一个最大的圆，此圆的半径是（）A. 6米B. 4米C. 3米D. 2米4.圆的位置由（）决定。

A．圆心 B．半径 C．直径5.半径等于直径的一半的条件是（）。

A．任一圆内B．圆心相同的圆内C．同圆或等圆中6.如图中梯形的上底是（）米．A．1 B．13 C．4 D．87.如图，在长方形中正好摆两个大小相等的圆，这个长方形的面积是（）平方厘米．A．324 B．54 C．162 D．127.17二、填空题1.________决定圆的位置，________决定圆的大小。

2.用圆规画圆，首先要确定圆的________和________。

3.把3.14、31.4%、3、三成四、π五个数从大到小排列（）﹥（）﹥（）﹥（）﹥（）4.画一个周长是18.84厘米的圆，圆规的两脚之间的距离应该是（）厘米。

5.在一个长4cm，宽3cm的长方形中，画一个最大的圆，圆的半径是厘米。

6．如图，有( )条对称轴，有( )条对称轴。

7.如图，其中一个圆的直径是cm，半径是cm，长方形的长是cm。

三、判断题1.圆的任意一条直径所在的直线都是圆的对称轴。

( )2.圆的周长总是它直径的π倍．( )3.在一个正方形内画两个最大的圆，正方形边长的一半等于圆的直径。

( )4.同一个圆中，直径是半径的2倍。

( )5.通过圆心的线段叫做圆的直径。

（）。

6.在长8厘米，宽6厘米的长方形中画一个最大的半圆，半圆的半径是4厘米。

( )四、解答题1.下图中，圆的直径是多少cm？长方形的宽是多少cm？2.如图四边形ABCD是平行四边形，圆O的半径r=3cm。

【考点精讲+期中期末通用讲义—北师大版】六年级上册数学单元考点精讲+优选易错题（基础版）01 圆一、圆的认识(一)1.圆的特征:由一条曲线围成的封闭图形，圆上任意一点到圆心的距离都相等。

在食指绕拇指旋转一周的过程中，拇指所按的点不变，食指与拇指间的距离不变。

2.圆的画法。

(1)手指画圆法。

以拇指为固定点，食指与拇指间的距离不变，将食指绕拇指旋转一周，食指的运动轨迹就形成了一个圆。

(2)实物画圆法。

把圆形物体放在纸上固定不动，用笔沿实物的边缘描一周，就画成了一个圆。

(3)系绳画圆法。

用一个图钉、一根线(没有弹力)和一支笔画圆的方法:用图钉将线的一端固定在一点上，用笔将线拉直并绕这个固定的点旋转一周，就画成了一个圆。

用图钉、线和笔画圆时，图钉要固定好，线要拉直。

(4)圆规画圆法。

根据圆心到圆上任意一点的距离(即半径)都相等，可以用圆规来画圆。

步骤如下:①把圆规的两脚分开，定好两脚间的距离(即半径);②把带有针尖的一只脚固定在一点(即圆心)上;③把带有铅笔的一只脚绕这个固定点旋转一周，就可以画出一个圆。

用圆规画圆，针尖所在的位置是圆心，两脚间的距离是半径。

3.圆的各部分名称。

(1)圆心。

画圆时，圆规带有针尖的脚所在的点叫圆心。

圆心一般用字母O表示。

(2)半径。

用圆规画圆时，圆规两脚之间的距离就是所画圆的半径，即圆心到圆上任意一点的距离叫半径。

半径一般用字母r表示。

在同一个圆里，所有半径的长度都相等。

1.同一个圆里有无数条半径，长度都相等。

2.直径是圆内最长的线段。

(3)直径。

通过圆心并且两端都在圆上的线段叫作直径。

直径一般用字母d表示。

在同一个圆里，所有直径的长度都相等。

4.圆的各部分之间的关系。

圆有无数条直径，无数条半径;同圆(或等圆)中的直径都相等，半径都相等;直径的长度是半径的2倍，可以表示为d=2r或r=d2。

5.圆心和半径的作用:圆心确定圆的位置，半径决定圆的大小。

6.圆在生活中的应用。

汽车车轮、自行车的车轮、球、齿轮、方向盘、圆规、井盖、钟表、水杯、环岛……1.判断直径和半径时，一定要看其是否经过圆心。

圆的认识(二)
1.填一填。

(1)把圆沿任何一条()对折,它的两边可以完全重合,这说明圆是
()图形,它有()条对称轴。

(2)至少将圆沿直径对折()次才能找到圆心。

(3)长方形有()条对称轴,正方形有()条对称轴,等腰三角形有()条对称轴,等边三角形有()条对称轴。

(4)在一个半径是2 cm的圆内,两端都在圆上的最长线段是()cm。

2.下面的图形是轴对称图形吗?如果是轴对称图形,在括号里写出有几条对称轴。

3.下面的图形是轴对称图形吗?画出轴对称图形的两条对称轴。

4.下面是一个圆形表盘,它的半径是多少?
5.在下面的正方形中画一个最大的圆,你如何确定圆心?画一画,找出圆心的位置。

6.(能力素养题)图中圆的位置发生了什么变化?
(1)从位置A向平移个格到位置B,再向平移个格到位置C。

(2)从位置C向平移个格到位置D,再向平移个格到位置E。

(3)从位置C到位置F,请你说说可以怎样平移?
7.用硬纸板做成下面三种图形,然后沿中心点转动,你发现了什么?
第2课时圆的认识(二)
1.(1)直径轴对称无数(2)2
(3)2413(4)4
2.略
3.略
4.2.8÷2=1.4(cm)
5.图略先画出正方形的两条对角线,对角线的交点就是圆心。

6.(1)右4右5(2)下3左 3
(3)从位置C先向左平移7个格,再向下平移3个格到位置F或从位置C先向下平移3个格,再向左平移7个格到位置F。

7.它们旋转一定的度数后与原图形重合。

《圆的认识(一)》一、我会填。

1、圆中心的一点叫( )，通常用字母( )表示，它决定了圆的( )。

2、通过( )，并且两端都在圆上的( )，叫作圆的直径，用字母( )表示。

直径是圆内两端都在圆上的所有线段中( )的一条。

3、从( )到圆上( )一点的线段叫作圆的半径，用字母( )表示，它决定了圆的( )。

4、时钟的分针转动一周形成的图形是( )，分针的长度是这个图形的( )。

5、在同圆或等圆内，( )的长度是( )长度的2倍，我们字母表示( )。

6、( )决定圆的大小，( )决定圆的位置。

二、 我会辩一辩。

1、圆的直径都相等。

( )2、同一个圆上所有的点到圆心的距离都相等。

( )3、直径一定比半径长。

( )4、半径是射线，直径是直线。

( )5、画圆时，圆规两脚间的距离就是圆的直径。

( ) 三、我会选。

(每题2分，共10分)1、一个圆有( )条直径。

新 课 标 第 一 网 A 、1 B 、2 C 、无数2、在一个边长是5㎝的正方形内，画一个最大的圆。

它的半径是( )。

A 、5㎝ B 、10㎝ C 、任意长 D 、2.5㎝3、圆的直径是半径的( )。

A 、2倍 B 、21C 、1.2倍 4、直径和半径都是( )。

A 、射线B 、直线C 、线段5、画圆时，圆规两脚分开4㎝，所画的圆的直径是( )㎝。

A 、2.5B 、4C 、8四、我会算。

半径（r）2cm 7dm 1.5m 直径（d） 1.2cm 9m 4.8cm五、我会画。

(每题5分，共20分)1、半径是2㎝的圆。

2、直径是3㎝的圆。

答案：一、1. 圆心，O，位置 2.圆心，线段，d,最长 3.圆心，任意，r，大小 4.圆，半径5.直径，半径，d=2r6.半径，圆心二、×√ × × ×三、C D A C C四、4 ，0.6,4.5,14,2.4,3《圆的认识（二）》课时练1.填表。

图形名称正方形等腰梯形等边三角形等腰三角形圆对称轴数2.填一填。

《圆的认识（一）》同步习题1.直接写出得数。

6.21÷3 3.14×27.2÷0.8 0.54÷0.9 9.42÷31 5×154×2313×13×27837×56×141534×56×8153.14×1 6.28÷2 8.5×2 9.3÷3 8.4÷0.04 2.想一想，填一填。

（1）圆心通常用字母（）表示，半径通常用字母（）表示，直径通常用字母（）表示。

（2）在同一个圆中，可以画（）条半径，它们的长度都（）；可以画（）条直径，它们的长度都（）。

（3）（）决定圆的位置，（）决定圆的大小。

3.选择。

（将正确答案的字母填在括号里）。

（1）直径和半径都是（）。

A.线段B.射线C.直线（2）以某一确定的点为圆心，可以画（）个圆。

A.1B.无数C.无法确定（3）在下面各图中，（）表示的是圆及其半径。

（4）在下面各图中，（）表示的是圆及其直径。

4.填表。

半径4dm 0.9m 3.3cm直径6m 10.48km 5.画一个直径是2cm的圆，用彩笔描出这个圆的圆心、半径和直径，并分别用字母O，r，d表示出来。

6.请你想一想，描述或画出书包可能在哪里。

7.请用自己的方式说明为什么车轮都要做成圆形的，车轴应该装在哪里。

参考答案1. 2.07 6.28 9 0.6 3.141 23813133.14 3.14 17 3.1 2102.（1）O r d（2）无数相等无数相等（3）圆心半径3.（1）A （2）B （3）B （4）C4.半径4dm 3m 0.9m 3.3cm 5.24km 直径8dm 6m 1.8m 6.6cm 10.48km5.略6.书包在以小女孩为圆心、半径为2m的圆周上。

7.略。

第一单元圆一、圆的认识（一）“练一练”1.围成圆形，每个人离中心位置都相等，观看表演的条件都差不多，比较公平。

利用了同一个圆中所有的半径都相等的知识。

2.略。

5.（1）圆的半径是（4cm）,直径是（8cm）。

（2）圆的半径是（3cm），直径是（6cm）。

（3）长方形的长是（4cm），直径是（2cm）。

6.在没有圆规的情况下，能用哪些方法画圆：沿着圆形物体的边缘描圆；用钉、笔和线结合起来画圆等。

（答案不唯一，学生回答合理即可）7.圆形容易滚动搬运，圆形物体放置在配套的卡槽里后，不容易掉落。

物体调入水中所产生的水波向四周扩散的速度是一样的，故水波是圆的。

8.略。

二、圆的认识（二）“练一练”1.下面的图形都是轴对称图形，第一个图形有无数条对称轴，第二个图形有三条对称轴，第三个图形有两条对称轴，第四个图形有三条对称轴。

（画图过程略，画出其中的两条即可）2.（1）1元硬币的直径是25mm。

（2）略。

3.（1）从位置A向右平移4个方格到位置B，再向右平移6个方格到位置C。

（2）从位置C向下平移3个方格到位置B，再向左平移2个方格到位置C。

（3）先向右平移8个方格，再向下平移2个方格或者先向下平移2个方格，再向右平移8个方格。

（答案不唯一）4.正方形每旋转90度就与原图重合，旋转一周与原图重合4次；等边三角形每旋转120度就与原图重合，旋转一周与原图重合3次；圆旋转任意角度都与原图重合，旋转一周与原图重合无数次。

三、欣赏与设计“练一练”1.（1）画图时注意以不同的点为圆心，画半圆或者14⁄圆。

（2）画图时注意中间的4个小圆的圆心位置和半径长度。

2.旋转时，黑点形成的痕迹是一个圆形。

3.略。

4.（1）一个正方形，围绕中心点旋转很多次后，中间会逐渐形成一个圆形。

（2）图上分别出示了正三角形、正方形、正五边形、正六边形……正多边形的边越多，越接近圆形。

四、圆的周长“练一练”1.（1）可以用“滚动法”或“绕线法”量出圆的周长。

北师大版六年级数学上册全册课时练习第一单元圆 (2)第1课时圆的认识（一） (2)第2课时圆的认识（二） (3)第3课时欣赏与设计 (4)第4课时圆的周长 (5)第5课时圆周率的历史 (6)第6课时圆的面积（一） (6)第7课时圆的面积（二） (7)第二单元分数混合运算 (8)第1课时分数混合运算（一） (8)第2课时分数混合运算（二） (9)第3课时分数混合运算（三） (10)第三单元观察物体 (12)第1课时搭积木比赛 (12)第2课时观察的范围 (13)第3课时天安门广场 (14)第四单元百分数 (15)第1课时百分数的认识 (15)第2课时合格率 (16)第3课时营养含量 (17)第4课时这月我当家 (18)第五单元数据处理 (19)第1课时扇形统计图 (19)第2课时统计图的选择 (21)第3课时身高的情况 (22)第4课时身高的变化 (25)第六单元比的认识 (26)第1课时生活中的比 (26)第2课时比的化简 (27)第3课时比的应用 (29)数学好玩 (31)第1课时反弹高度 (31)第2课时看图找关系 (32)第3课时比赛场次 (33)第七单元百分数的应用 (34)第1课时百分数的应用（一） (34)第2课时百分数的应用（二） (35)第3课时百分数的应用（三） (37)第4课时百分数的应用（四） (38)总复习 (39)第1课时数与代数 (39)第2课时图形与几何 (41)第3课时统计与概率 (43)第一单元圆第1课时圆的认识（一）一、填空题。

1.圆中心的一点叫作（），用字母（）表示，它到圆上任意一点的距离都（）。

2.（）叫作半径，用字母（）表示。

3.（）叫作直径，用字母（）表示。

4.在一个圆里，有（）条半径，有（）条直径。

5.（）确定圆的位置，（）确定圆的大小。

二、选择题。

1.圆是平面上的封闭的（）。

A.直线图形B.曲线图形C.无法确定2.圆中两端都在圆上的线段（）。

A.一定是圆的半径B.一定是圆的直径C.无法确定3.圆的直径有（）条。

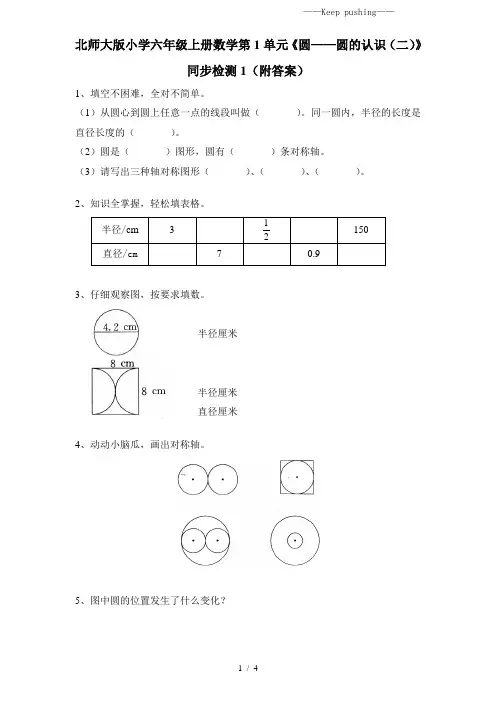
北师大版小学六年级上册数学第1单元《圆——圆的认识（二）》同步检测1（附答案）1、填空不困难，全对不简单。

（1）从圆心到圆上任意一点的线段叫做（ ）。

同一圆内，半径的长度是直径长度的（ ）。

（2）圆是（ ）图形，圆有（ ）条对称轴。

（3）请写出三种轴对称图形（ ）、（ ）、（ ）。

2、知识全掌握，轻松填表格。

3、仔细观察图，按要求填数。

半径厘米半径厘米直径厘米4、动动小脑瓜，画出对称轴。

5、图中圆的位置发生了什么变化？ 半径/cm 3 21 150 直径/cm 7 0.9（1）从位置A向平移个方格到位置B。

再向平移个方格到位置C。

（2）从位置C向平移个方格到位置D，再向平移个方格到位置E。

（3）从位置A向平移个方格，再向平移个方格到位置F。

6、我是小法官，对错我会判。

（1）通过圆心的线段就是直径。

（）（2）圆的对称轴一定通过圆心。

（）（3）圆上任意一点到圆心的距离都相等。

（）7、脑筋转转转，答案全发现。

（1）直径和半径的关系是（）A、直径等于两个半径B、半径总是直径的一半C、在同一圆里，直径等于半径的2倍（2）一个圆至少对折（）次，就可以找到圆心。

A、两B、三C、一（3）只有1条对称轴的是（）A、圆B、长方形C、等腰三角形8、有两个圆，大圆直径是小圆半径的4倍，大圆半径和小圆直径是否相等？为什么？答案：11、（1）半径2（2）轴对称无数（3）圆长方形正方形5、（1）下 3 右 4（2）右 6 上 2（3）右 6 下 1 或下 1 右 66、（1）×（2）√（3）√7、（1）C （2）A （3）C8、提示：可设小圆半径为r，由大圆直径是小圆半径的4倍可推出大圆直径为4r，则大圆半径为2r，小圆直径为2r，所以大圆半径和小圆直径相等。

版权声明：所有试题为柏成教育培训机构下属网站(柏成家教网)收集整理。

用于下属淘宝店（柏成教育淘宝店，掌柜ID:柏成教育网）出售使用。

如果亲不是在以上店铺购买的试题，本公司及店铺不对试题的质量及售后负任何责任！。

章节预习讲义（北师大版）北师大版数学六年级上册章节预习第一单元《圆》知识互联知识点一：圆的认识 O A Br Cd1.圆的圆心、半径和直径分别用字母O 、r 、 d 表示。

2.常用的画圆的方法有：手指画圆、绕绳画圆、圆规画圆。

3.同圆或等圆中，直径是半径的2倍，半径是直径的一半，用字母表示：d ＝2r ，12r d =。

4.圆心决定圆的位置，半径决定圆的大小。

5.圆的对称性：圆是轴对称图形，每一条直径所在的直线都是圆的对称轴。

6.找轴对称图形的对称轴的方法：① 观察轴对称图形由哪些常见的轴对称图形组成；② 再把轴对称图形对折，直到完全重合，③ 折痕所在的直线就是我们要找的对称轴。

7.利用圆可以设计出美丽、有趣的图案，设计图案：①先观察、分析图案的组成，②再单独或综合运用平移、旋转和轴对称等知识。

知识点二：圆的周长1.圆的周长就是围成圆一周的曲线的长。

2.常用的圆周长的测量方法：滚动法、绕线法。

3.圆的周长＝直径×圆周率，C d π＝或C r π＝2圆周率是圆的周长除以直径的商，用字母π表示，计算时通常取3.14。

知识导航4.求组合图形或不规则图形的周长时，可以采用转化法把它转化成规则图形。

知识点三：圆的面积C ÷2长宽r1.圆的面积的估算方法：将圆剪拼成“平行四边形”再求面积。

2.圆的面积的计算公式：圆的面积=圆周率×半径的平方，用字母表示为S=πr2。

3．求阴影部分的面积有时可以将阴影部分转化成已学过的平面图形来计算；4．计算环形面积的关键是找出内圆半径和外圆半径。

一、精挑细选（共5题；每题2分，共10分）1．(本题2分)（2021·辽宁六年级课时练习）圆是平面上的（ ）。

A ．直线图形B ．曲线图形C ．无法确定2．(本题2分)（2019·深圳市龙华区锦华实验学校六年级期中）下列图形中对称轴条数最多的是（）。

A ． B ． C ． D ．3．(本题2分)（2021·仁寿县三溪乡中心小学六年级期末）一个半径增加2cm 的圆，它的周长增加了（）。

第1课时圆的认识（一）一、填空题。

1.圆中心的一点叫作（），用字母（）表示，它到圆上任意一点的距离都（）。

2.（）叫作半径，用字母（）表示。

3.（）叫作直径，用字母（）表示。

4.在一个圆里，有（）条半径，有（）条直径。

5.（）确定圆的位置，（）确定圆的大小。

二、选择题。

1.圆是平面上的封闭的（）。

A.直线图形B.曲线图形C.无法确定2.圆中两端都在圆上的线段（）。

A.一定是圆的半径B.一定是圆的直径C.无法确定3.圆的直径有（）条。

A.1B.2C.无数参考答案：一、1.圆心 O 相等 2.圆心到圆上任意一点的线段 r 3.通过圆心并且两端都在圆上的线段 d 4.无数无数 5.圆心半径二、1.B 2.C 3.C第2课时圆的认识（二）三、填空题。

1.圆是（）对称图形，有（）条对称轴。

2.圆的对称轴是（）所在的直线。

二、画出下面各图形的对称轴。

三、画出轴对称图形的另一半。

参考答案：一、1.轴无数 2.直径二、三、第3课时欣赏与设计四、欣赏下面的图形，它们有什么特点？五、分别以所给图形的顶点为圆心，以图形的边长为半径画圆，看能组成怎样的图案。

参考答案：一、都是轴对称图形。

二、第4课时圆的周长六、用彩笔描出下面圆或半圆的周长。

七、填表。

半径/m 直径/m 圆的周长/m参考答案：一、略 二、第5课时 圆周率的历史八、人类对计算圆周率的探索一直没有停止过，电子计算机的出现带来了计算圆周率的突破性进展，也使计算圆周率具有现实价值。

九、人类研究圆周率的历史漫长，探索的过程艰难，但人类始终没有放弃对真理的追求。

第6课时 圆的面积（一）十、判断题。

1.圆的面积就是围成圆的曲线的长度。

（ ）2.圆的面积就是圆所占平面的大小。

（ ）3.圆的面积就是圆所占空间的大小。

（ ）4.圆的半径越大，圆所占的面积也越大。

（ ） 二、填空题。

将一个半径为4cm 的圆平均分成若干份，拼成一个近似的平行四边形，那么这个平行四边形的底为圆的周长的一半，是（ ）cm ；高为圆的（ ），是（ ）cm 。

六上第一章：圆练习题一．选择题（共10小题）1．车轮滚动一周，所行的路程是求车轮的()A．直径B．周长C．面积2．草坪内旋转式水龙喷头的射程是5米，5米相当于圆的()A．半径B．直径C．周长D．面积3．在一个边长6分米的正方形中画一个最大的圆，圆的半径是（）分米.A．8B．6C．4D．34．一个半圆的半径是r，它的周长是()A.πrB.πr+2r C．2πr5．如图，以大圆的半径为直径画一小圆，大圆的周长是小圆周长的（）倍.A．2B．4C．6D．86．圆的半径扩大3倍，面积扩大()A．3倍B．6倍C．9倍7．有大、小两个圆，大圆半径是5厘米，小圆半径是4厘米，小圆面积是大圆面积的() A．B．C．倍8．用同样长铁丝围成长方形、正方形和圆形，则围成的（）面积最大.A．长方形B．正方形C．圆形9．我国古代数学家祖冲之是世界上第一个把圆周率的值精确到小数点后第7位的人。

通常圆周率保留两位小数约是()A．3.13B．3.14C．3.15D．3.1610．用圆规画一个周长是12.56厘米的圆，圆规两脚之间的距离是()A．2厘米B．3厘米C．4厘米D．6厘米二．填空题（共6小题）11．连接和任意一点的线段叫做半径．决定圆的位置，决定圆的大小.12．一个环形的外圆直径是10cm，内圆直径是8cm，它的面积是cm2.13．一个挂钟时针长5厘米，它的尖端一昼夜走了厘米.14．李师傅想把3根横截面直径都是10厘米的圆木用铁丝紧紧地捆绑在一起（如图），捆一圈（接头处不计）至少需铁丝厘米.15．图中阴影部分的周长是厘米．（单位：厘米）16．把一个圆等分成16份，拼成一个近似的长方形，周长增加了6cm，这个圆的面积是2cm.17．两端都在圆上的线段是圆的直径．．（判断对错）18．周长相等的两个圆，它们的面积一定相等．（判断对错）19．半圆的周长就是圆周长的一半．（判断对错）20．圆越大圆周率越大，圆越小圆周率越小．．（判断对错）四．计算题（共5小题）21．计算如图所示各圆的周长和面积.（1）（2）22．求下列图形的周长.23．求阴影部分的面积．（单位：厘米）24．在一个圆内作一个最大的正方形（如图）．已知正方形的面积是8平方厘米，则圆的面积是多少平方厘米？25．求下面图形中阴影部分的周长和面积.26．摩天轮的半径大约是10米，笑笑坐着它转动5周，她大约在空中转过多少米？27．某小区门口有一块圆形空地，直径是12米，现在要给这块地全部铺草皮，如果每平方米草皮的价格是10元，那么铺满草皮需要多少元？28．一种洒水车的前轮直径是6分米，如果它每分钟转3周，它每分钟前进多少米？29．公园中圆形花坛的周长是31.4m.（1）这个花坛的占地面积是多少平方米？（2）如果要在这个花坛的周围铺一条宽为1m的小路，这条小路的面积是多少平方米？30．某一圆形草地的周长是31.4米，其中的面积种植月季，其余是草皮．种植草皮的面积是多少平方米？六上（北师版）第一章：圆练习题参考答案与试题解析一．选择题（共10小题）1．车轮滚动一周，所行的路程是求车轮的()A．直径B．周长C．面积【分析】车轮滚动一周，所行的路程就是这个车轮的周长，可采用化曲为直的方法进行计算.【解答】解：车轮滚动一周所行的路程就是车轮一周的长度，即周长.答：车轮滚动一周，所行的路程是求车轮的周长.故选：B.【点评】此题主要考查的是利用圆的周长求车轮的所行路程.2．草坪内旋转式水龙喷头的射程是5米，5米相当于圆的()A．半径B．直径C．周长D．面积【分析】旋转式水龙喷头的射程是5米，喷头相当于圆的圆心，而射程是圆心出发到圆上任意一点的距离，此距离处处相等，所以射程5米就是指圆的半径；据此解答.【解答】解：旋转式水龙喷头的射程是5米，5米就是指圆的半径.故选：A。

最新资料欢迎阅读[ 六年级上册数学同步习题- 第一单元 ,,圆 ,1, 圆的认识 ( 一 ), 北师大版（ 20XX秋）含答案 ]作业 2【基础稳固】 1.(基础题)想想,填一填。

(1)圆中心的一点叫作 () 。

(2) 经过 () 而且两头都在圆上的 () 叫作圆的直径。

(3)在同一个圆或相等的圆中 , 全部的半径长度都 (); 全部的直径长度都 () 。

直径的长度是半径的 () 。

(4)画一个直径为 4 厘米的圆 , 那么圆规两脚间的距离应当是() 厘米。

(5)以一点为圆心能够画出 () 个圆。

2.(难点题)判断对错。

(1)经过圆心的线段是这个圆的直径。

() (2)圆心到圆上随意一点的距离都相等。

() (3)直径是一个圆内最长的线段。

() (4)圆规两脚间的距离是 3 厘米 , 画出的圆的直径是 3 厘米。

() (5)两头在圆上的线段是直径。

() 3.(要点题)指出下边圆的直径和半径。

【提高培优】 4.(操作题 )(1) 以 B点为圆心 , 画一个直径是 3 厘米的圆, 并标出它的一条半径和一条直径。

·B (2)在一个长 8 厘米 , 宽 3 厘米的长方形里画最大的圆 ,最多能够画几个 ? 5.(要点题)下列图中大圆的直径是10 cm,请你求出小圆的半径。

【思想创新】 6.( 研究题 ) 看图填空。

(1)图中已学过的图形有 () 、() 、()、()。

(2)正方形的周长是 (), 小圆的直径是 () 。

(3)直角梯形的高是 (), 上底长是 (),下底长是 (),面积是 () 。

(4)大三角形的最长的边长是 (), 相对应的高是 (), 面积是()。

【参照答案】作业 2:1.(1) 圆心(2)圆心线段(3) 相等相等2 倍(4)2 (5) 无数 2.(1) ?(2) √(3) √(4) ?(5) ?3.AB OC(或 OA或 OB)EF OD(或 OF或 OE)4.(1) 略(2)最多能够画 2个(绘图略)5.10÷2 - 2=3(cm)6.(1)三角形圆形梯形正方形(2)20 cm 5 cm(3)5 cm5 cm10 cm 37.5 cm2(4)10 cm 5 cm25 cm2。

北师大版数学六年级上册第一章第二节圆的认识同步练习选择题一个圆有（）直径。

A.1条B.2条C.无数【答案】C【解析】根据直径的含义：圆有无数条直径。

此题考查圆的特征的基础知识，平时应注意基础知识的积累。

掌握经过圆心，并且两点都在圆上的线段，叫做直径；在圆中有无数条直径。

选择题某点到一圆的圆心距离大于半径，该点在（）A.圆内B.圆上C.圆外【答案】C【解析】圆上的点到圆心的距离等于半径，所以到圆心距离等于半径的点在圆上；圆外的点到圆心的距离大于半径，所以到圆心距离大于半径的点在圆外；圆内的点到圆心的距离小于半径，所以到圆心距离小于半径的点在圆内。

根据圆上点，圆外点及圆内点到圆心的距离与圆的半径的关系，可以由点到圆心的距离得到点的位置。

选择题画一个直径是2厘米的圆，圆规两脚间的距离应是（）A.1厘米B.2厘米C.4厘米【答案】A【解析】2÷2＝1（厘米）所以，圆规两脚间的距离应是1厘米。

根据圆的认识，同圆或等圆中半径和直径之间的关系，d＝2r ，掌握圆规两脚间的距离即半径。

选择题在下面物体中，表面是圆形的物体是（）A.硬币B.数学课本C.方木条【答案】A【解析】因为硬币的表面是圆形的；数学课本的表面是长方形的；方木条的表面是正方形；所以，表面是圆形的物体是硬币。

考查了圆的特征，应注意基础知识的积累和应用，结合生活实际解答。

选择题下面说法错误的是（）A.圆是一种曲线图形B.半径一定比直径短C.圆是轴对称图形【答案】B【解析】圆是一种曲线图形，而且是轴对称图形有无数条对称轴；在同一个圆内半径一定比直径短，但是如果不在同一圆内就不一定了；所以半径一定比直径短的说法错误。

根据圆的特征解答问题，圆是一种曲线图形，而且是轴对称图形有无数条对称轴；在同一个圆内半径一定比直径短，但是如果不在同一圆内就不一定了，注意知识的灵活掌握。

判断题直径是2厘米的圆小于半径是2厘米的圆。

【答案】正确【解析】因为2÷2＝1（厘米）1厘米＜2厘米；所以直径是2厘米的圆小于半径是2厘米的圆。

北师大版六年级上册同步练习之《1.1 圆的认识与圆周率》一．填空题（共10小题）1．战国时期《墨经》一中记载“圆,一中同长也。

”表示圆心到圆上各点的距离都相等,即都相等。

2．圆的周长和的比值叫做圆周率,世界上第一个把圆周率的值精确到7位小数的人是。

3．画圆时,决定圆的位置,决定圆的大小．4．看图填空。

r＝cm。

d＝cm。

5．圆的位置由确定．6．圆心确定圆的,半径确定圆的,圆是轴对称图形,直径所在的直线是圆的；圆的周长与它的直径的比值是一个,我们把它叫做,用字母表示,计算时通常取它的近似值。

7．早在二千多年前,我国古代就有了关于圆的精确记钱,《墨经》中描述道：“圆,一中同长也”,这句话描述的是圆的什么特征：。

8．为了保持车辆的平稳行驶,车轮平面轮廓采用圆形,这是利用了的特征。

9．圆的周长与它的的比值叫做圆周率,它起一个小数。

10．填表。

半径 2.5dm直径 3.6m二．选择题（共8小题）11．图中大圆的直径是（）毫米．A．12B．10C．44D．2212．（）决定圆的位置．A．圆心B．半径C．直径13．从一个半径为0.5厘米的圆上取一点,在直线上从“0”开始滚动一周后,这个点的位置大约是（）A．B．C．D．14．圆周率是圆的周长和直径的比值,如果如图中线段AB表示一个圆的周长,那么这个圆的直径可能是（）A．线段AB B．线段AC C．线段AD D．线段DE 15．《墨子•经上》记载：“圆,一中同长也”,这句话的内涵解释正确的是（）A．同一圆中,所有的半径都相等B．同一圆中,所有的直径都相等C．以上说法都正确16．（）不能决定圆的大小．A．圆心B．圆的直径C．圆的周长17．下列说法中,错误的是（）A．圆的中心位置由圆心决定B．一个圆里的直径有无数条C．在一个圆里,所有的半径都相等D．连接圆上两点的线段叫做圆的直径18．在一个长5cm、宽3cm的长方形中画一个最大的圆,该圆的半径是（）。

A．5cm B．3cm C．2.5cm D．1.5cm三．判断题（共9小题）19．一张纸至少对折两次,才能找到圆心。