逐点比较法直线插补圆弧插补实例

1、概述在机床的实际加工中，被加工工件的轮廓形状千差万别，各式各样。

严格说来，为了满足几何尺寸精度的要求，刀具中心轨迹应该准确地依照工件的轮廓形状来生成。

然而，对于简单的曲线，数控装置易于实现，但对于较复杂的形状，若直接生成，势必会使算法变得很复杂，计算机的工作量也相应地大大增加。

因此，在实际应用中，常常采用一小段直线或圆弧去进行逼近，有些场合也可以用抛物线、椭圆、双曲线和其他高次曲线去逼近（或称为拟合）。

所谓插补是指数据密化的过程。

在对数控系统输入有限坐标点（例如起点、终点）的情况下，计算机根据线段的特征（直线、圆弧、椭圆等），运用一定的算法，自动地在有限坐标点之间生成一系列的坐标数据，即所谓数据密化，从而自动地对各坐标轴进行脉冲分配，完成整个线段的轨迹运行，以满足加工精度的要求。

机床数控系统的轮廓控制主要问题就是怎样控制刀具或工件的运动轨迹。

无论是硬件数控（NC）系统，还是计算机数控（CNC）系统或微机数控（MNC）系统，都必须有完成插补功能的部分，只是采取的方式不同而已。

在CNC或MNC中，以软件（程序）完成插补或软、硬件结合实现插补，而在NC中有一个专门完成脉冲分配计算（即插补计算）的计算装置——插补器。

无论是软件数控还是硬件数控，其插补的运算原理基本相同，其作用都是根据给定的信息进行数字计算，在计算过程中不断向各个坐标发出相互协调的进给脉冲，使被控机械部件按指定的路线移动。

有关插补算法问题，除了要保证插补计算的精度之外，还要求算法简单。

这对于硬件数控来说，可以简化控制电路，采用较简单的运算器。

而对于计算机数控系统来说，则能提高运算速度，使控制系统较快且均匀地输出进给脉冲。

经过多年的发展，插补原理不断成熟，类型众多。

从产生的数学模型来分，有直线插补、二次曲线插补等；从插补计算输出的数值形式来分，有基准脉冲插补（又称脉冲增量插补）和数据采样插补。

在基准脉冲插补中，按基本原理又分为以区域判别为特征的逐点比较法插补，以比例乘法为特征的数字脉冲乘法器插补，以数字积分法进行运算的数字积分插补，以矢量运算为基础的矢量判别法插补，兼备逐点比较和数字积分特征的比较积分法插补，等等。

② 具有固定的过象限顺序。 逆圆弧：NR1 → NR2 → NR3 → NR4 → NR1 →• • • 顺圆弧：SR1 → SR4 → SR3 → SR2 → SR1 →• • •
③ 过象限圆弧与坐标轴必有交点，当动点处在坐标轴上时必有 一个坐标值为零。此点可以作为过象限的标志。
④ 终点判别不能简单地直接使用前述的三种方法，否则将丢失 一部分圆弧轮廓。
型 进给 新位置坐标
新位置偏差
Fi ≺ 0
进给 新位置坐标
新位置偏差
SR1 -Y X i1 X i Yi1 Yi 1
Fi1 Fi 2Yi 1 +X
X i1 X i 1 Yi1 Yi
Fi1 Fi 2Xi 1
NR1
-X
X i1 X i 1 Yi1 Yi
Fi1 Fi 2Xi 1
+Y
O
0°
45°
90°X
根据根据上式和该图可得如下结论：
① 当刀具沿着平行于坐标轴的方向进行切削时，合成进给速度最 大，等于脉冲源进给速度；当刀具沿其他方向切削时，合成进给速度 总是小于脉冲源进给速度。
② 直线插补合成进给速度是恒定的，但其值随插补直线与X轴的 夹角而变化，其变化范围为（0.707—1.0）vMF 。
③ SR1 → NR1：X轴、Y轴对调 NR1 → SR1：X轴、Y轴对调
采用对称性处理方法，四象限圆弧插补问题的统一处理算法如下。
线
Fi ≥ 0
型 坐标进给 新位置偏差值计算
SR1
-Y
NR2
-Y
SR3
+Y
NR4
+Y
Fi1 Fi 2 | Yi | 1 | Yi1 || Yi | 1

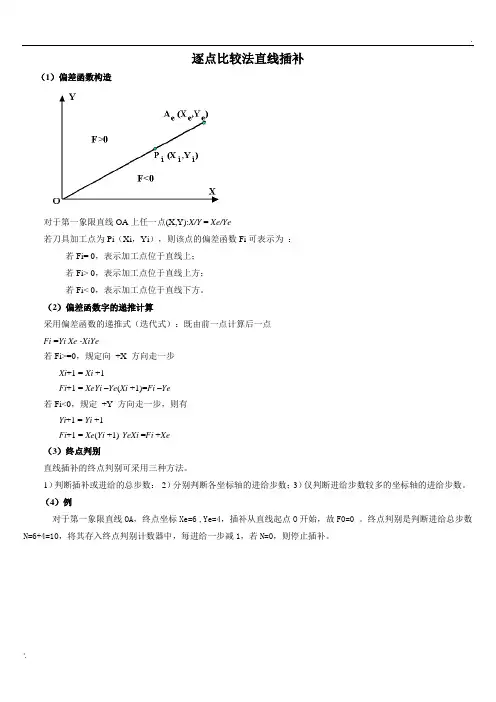
逐点比较法直线插补（1）偏差函数构造对于第一象限直线OA上任一点(X,Y):X/Y = Xe/Ye若刀具加工点为Pi（Xi，Yi），则该点的偏差函数Fi可表示为：若Fi= 0，表示加工点位于直线上；若Fi> 0，表示加工点位于直线上方；若Fi< 0，表示加工点位于直线下方。

（2）偏差函数字的递推计算采用偏差函数的递推式（迭代式）：既由前一点计算后一点Fi =Yi Xe -XiYe若Fi>=0，规定向+X 方向走一步Xi+1 = Xi +1Fi+1 = XeYi –Ye(Xi +1)=Fi –Ye若Fi<0，规定+Y 方向走一步，则有Yi+1 = Yi +1Fi+1 = Xe(Yi +1)-YeXi =Fi +Xe（3）终点判别直线插补的终点判别可采用三种方法。

1）判断插补或进给的总步数：2）分别判断各坐标轴的进给步数；3）仅判断进给步数较多的坐标轴的进给步数。

（4）例对于第一象限直线OA，终点坐标Xe=6 ,Ye=4，插补从直线起点O开始，故F0=0 。

终点判别是判断进给总步数N=6+4=10，将其存入终点判别计数器中，每进给一步减1，若N=0，则停止插补。

逐点比较法圆弧插补（1）偏差函数构造任意加工点Pi（Xi，Yi），偏差函数Fi可表示为若Fi=0，表示加工点位于圆上；若Fi>0，表示加工点位于圆外；若Fi <0，表示加工点位于圆内（2）偏差函数的递推计算1） 逆圆插补若F ≥0，规定向-X 方向走一步若Fi<0，规定向+Y 方向走一步2） 顺圆插补若Fi ≥0，规定向-Y 方向走一步若Fi<0，规定向+y 方向走一步（3）终点判别1）判断插补或进给的总步数： 2）分别判断各坐标轴的进给步数： （4）例对于第一象限圆弧AB ，起点A （4，0），终点B （0，4）⎩⎨⎧+-=-+-=-=++12)1(122211i i i i i ii X F R Y X F X X ⎩⎨⎧++=-++=+=++12)1(122211i i i i i i i Y F R Y X F Y Y ⎩⎨⎧+-=--+=-=++12)1(122211i i i i i i i Y F R Y X F Y Y ⎩⎨⎧++=-++=+=++12)1(122211i i i i i i i X F R Y X F X X ba b a Y Y X X N -+-=ba x X X N -=b a y Y Y N -=。

Y B(xe,ye)
M(xm,ym)
Rm R
A(x0,y0)
O 图3 圆弧插补原理图 X
圆弧插补原理参见上图，对于第一象限逆圆，设圆弧的起点为 A(x0,y0)，终点为 B(xe,ye)， 圆弧半径为 R。加工点为 M(xm,ym)，它与圆心的距离为 Rm，则
（1）偏差计算
Fm
=
Rm2
− R2
=
xm2
p102=p102-p104 p101=p101+1 x-0.1 else p102=p102+p103 p101=p101+1 y0.1
；计算新的偏差值（Fi+1=Fi－ya） ；步数计数器加一 ；X方向进分别是（-0.1 -0.5 -1.0） ；偏差判别（若P102小于0表示刀具在直线下方） ；计算新的偏差值（Fi+1=Fi＋xa） ；步数计数器加一 ；Y方向进给分别是（0.1 0.5 1.0）
endif
endwhile
close
（3）根据直线插补编成格式，编写所给圆弧插补程序。 各组的圆弧的插补任务是： u 第一组：圆弧半径 50，第二象限顺圆；
第二组：圆弧半径 50，第二象限逆圆； 第三组：圆弧半径 60，第三象限顺圆； 第四组：圆弧半径 60，第三象限逆圆； 第五组：圆弧半径 70，第四象限顺圆； 第六组：圆弧半径 70，第四象限逆圆； open prog7 clear linear inc p101=0 p102=0 p103=0 p104=50 while(p101!>100) if(p102!<0) y0.5 p101=p101+1 p102=p102-2*p104+1 p104=p104-1 else -x0.5 p101=p101+1 p102=p102-2*p103+1 p103=103-1 endif endwhile close

实验报告实验内容：逐点比较法直线和圆弧插补2011年9月25日院系:物科院班级：085 学号：07080518 姓名：陈实实验目的：利用逐点比较法的插补原理，编写直角坐标系下的直线、圆弧插补程序，观察屏幕上仿真的运动轨迹，掌握逐点比较法的插补原理。

实验原理：逐点比较发是基于动点与理想曲线院函数的比较来实现插补的。

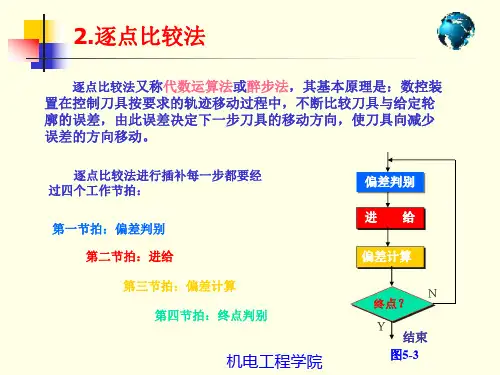
逐点比较法的插补过程，每走一步要进行一下四个步骤：偏差判别：根据偏差值确定刀具相对加工曲线的位置坐标进给：根据偏差判别的结果，决定控制线沿哪个坐标进给一步以接近曲线偏差计算：计算新加工店相对曲线的偏差，作为下一步偏差判别的依据终点判别：判别是否到达终点，未到达终点则返回第一步继续插补，到终点则停止1、逐点比较法直线插补原理：逐点比较法在第一象限的直线插补原理如下图所示，其他象限情况可依次类推。

现加工OE直线，如果刀具动点在OE直线上方或在线上，则令刀具沿X正方向进给一步；若刀具动点在OE直线下方，则令刀具沿Y轴正方向进给一步，如此循环直到加工到E点。

判别刀具动点的位置根据偏差函数判别公式：根据这个公式可以推到出两种不同情况下的地推公式：对于插补终点的判别，可以采用单向的计数长度法，即：取计数长度M等于Xe、Ye中的大者，并设该坐标方向为计数方向。

插补时，仅在该方向上产生进给时，计数长度减一。

图1的逐点比较法中，工作循环的结束条件就是M减为0.2、逐点比较法圆弧插补原理：逐点比较法在第一象限的圆弧插补原理如图所示，其他象限可一次类推：对于第一象限的逆圆弧，如果动点在圆弧的外侧则令刀具动点沿X轴负方向进给一步。

如果动点在圆弧的内侧则令刀具沿Y轴正方向进给一步。

圆弧的偏差计算公式为：根据这个公式同样可推导出圆弧插补的两种不同情况下的递推公式：对于插补终点的判别，同样可以采用单向的计数长度法，不过对于圆弧，计数的方向并不取决于终点坐标中的大者，而是取决于圆弧终点处。

逐点比较法插补中需要编写插入部分流程图：插入程序：intM,Fi=0,Fi0,Fi1,xi,yi,i=0 ,num=-1;bool Gx; M=Xe+Ye;moveto(x0,y0);setcolor(10);line(x0,y0,x0+Xe*delta,y0-Ye*delta);xi=x0;yi=y0;setcolor(12);while(M>0){getch();if(Fi>=0){linerel(delta,0); xi=xi+delta;Fi0=Fi-Ye;Fi=Fi0; num++;dis_msg(num,Fi,1,0,Fi0,M);}else{linerel(0,-delta);Fi1=Fi+Xe;yi=yi-delta;Fi=Fi1;num++;dis_msg(num,Fi,0,1,Fi1,M);}M--;}圆弧插补实验程序：int M,Fi=0,Fi0,Fi1,xi=R,yi=0,i=0,num=0; M=R;setcolor(10);moveto(x0,y0);arc(x0,y0,0,90,R*delta);setcolor(12);moveto(x0+xi*delta,y0);while(M>0){getch();if(Fi>=0){linerel(-delta,0);Fi0=Fi-2*xi+1;Fi=Fi0;xi=xi--;M--;dis_msg(num,Fi,1,0,Fi0,M);}else{linerel(0,-delta);Fi1=Fi+2*yi+1;Fi=Fi1;yi=yi++;dis_msg(num,Fi,0,1,Fi1,M);}num=num++;}实验中所遇问题分析：1、圆弧插补：Fi0与Fi1的计算，xi，yi计算先写入为：Fi0=Fi-2*xi*delta+1;Fi1=Fi+2*yi*delta+1;xi=xi-delta;yi=yi+delta;但是，实行以后出现的结果不正确，如图，分析：2、关于计数长度M：在直线插补中使用的是双向计数长度 M=xe+ye，插补路线会比较准确。

逐点比较法圆弧插补逐点比较法圆弧插补过程与直线插补过程类似，每进给一步也都要完成四个工作节拍：偏差判别、坐标进给、偏差计算、终点判别。

但是，逐点比较法圆弧插补以加工点距圆心的距离大于还是小于圆弧半径来作为偏差判别的依据。

如图5-7所示的圆弧AB，其圆心位于原点O（0，0），半径为R，令加工点的坐标为P（xi，yj），则逐点比较法圆弧插补的偏差判别函数为当F＝0时，加工点在圆弧上；当F＞0时，加工点在圆弧外；当F＜0时，加工点在圆弧内。

同插补直线时一样，将Fi，j=0同Fi，j＞0归于一类。

下面以第一象限圆弧为例，分别介绍顺时针圆弧和逆时针圆弧插补时的偏差计算和坐标进给情况。

1．插补第一象限逆圆弧1）当Fi，j≥0时，加工点P（xi，yj）在圆弧上或圆弧外，－X方向进给一个脉冲当量，即向趋近圆弧的圆内方向进给，到达新的加工点Pi－1,j，此时xi －1=xi－1，则新加工点Pi－1,j的偏差判别函数Fi－1，j为（2）当Fi，j＜0时，加工点P（xi，yj）在圆弧内，＋Y方向进给一个脉冲当量，即向趋近圆弧的圆外方向进给，到达新的加工点Pi,j＋1，此时yj+1=yj＋1，则新加工点Pi,j＋1的偏差判别函数Fi，j+12．插补第一象限顺圆弧1）当Fi，j≥0时，加工点P（xi，yj）在圆弧上或圆弧外，－Y方向进给一个脉冲当量，即向趋近圆弧的圆内方向进给，到达新的加工点Pi，,j－1，此时yj－1=yj－1，则新加工点Pi，j－1的偏差判别函数Fi，j－1为2）当Fi，j＜0时，加工点P（xi，yj）在圆弧内，＋X方向进给一个脉冲当量，即向趋近圆弧的圆外方向进给，到达新的加工点Pi＋1,j，此时xi＋1=xi ＋1，则新加工点Pi＋1,j的偏差判别函数为Fi+1，j由以上分析可知，新加工点的偏差是由前一个加工点的偏差Fi，j及前一点的坐标值xi、yj递推出来的，如果按式（5-6）、（5-7）、（5-8）、（5-9）计算偏差，则计算大为简化。

开始 初始化 Xe→X，Ye→Y 0→Fi ，N ＝|Xe|＋|Ye|
Y 进给方向：+X
F≥0 N 进给方向: +Y
Fi- Ye → Fi+1
Fi+ Xe → Fi+1
N ＝ N -1
N =0
N
Y 结束
继续
逐点比较法Ⅰ象限直线插补流程图
例题：设欲加工第一象限直线OE，起点为坐标原点，
终点坐标为Xe=4，Ye=3，用逐点比较法插补之，并画出
+Y F6 F5 2Y5 1 4
-X F7 F6 2X6 1 1
8
F7>0
-X
F8 F7 2X7 1 0
坐标计算
X0=4,Y0=0 X1=3,Y1=0 X2=3,Y2=1 X3=3,Y3=2 X4=3,Y4=3 X5=2,Y5=3 X6=2,Y6=4 X7=1,Y7=4
X8=0,Y8=4
Fi 0, 朝 x 增大方向, Fi1 Fi ye Fi 0, 朝 y 增大方向, Fi1 Fi xe
5.2 脉冲增量插补 其它象限插补流程：
3.逐点比较法Ⅰ象限逆圆插补
（1）基本原理
①偏差判别 关键：寻找偏差函数F（x，y）
当动点N(Xi,Yi)位于圆弧上时有下式成立
Y
E(XeYe) Nˊ
X i2 Yi2 Xe2 Ye2 R2
当动点N(Xi,Yi)在圆弧外侧时，有下式成立
X i2 Yi2 Xe2 Ye2 R2
当动点N(Xi,Yi)在圆弧内侧时，有下式成立
O
N(Xi,Yi) R
N〞 S(XSYS)
X
X i2 Yi2 Xe2 Ye2 R2
I象限逆圆与动点之间的关系

即
Fi1 Fi X e
6
在插补计算、进给的同时还要进行终点判别。常用终点判 别方法是：
设置一个长度计数器，从直线的起点走到终点，刀具沿
X 轴应走的步数为X e，沿Y 轴走的步数为Ye，计数器中存入 X和Y两坐标进给步数总和∑＝∣Xe∣＋∣Ye∣，当X 或Y
坐标进给时，计数长度减一，当计数长度减到零时，即∑＝ 0时，停止插补，到达终点。
终点判别：判断是否到达终点，若到 达x ，结束插补；否则，继续以上四个
步骤（如图3-3所示）。
图3-3 逐点比较法工作循环图
3
2. 直线插补
图3-4所示第一象限直线OE为给定轨迹，其方程为
XeY－XYe＝0
(3-1)
P（X，Y）为动点坐标，与直线的关系有三种情况：
（1）若P1点在直线上方，则有XeY－XYe>0 E （2） 若P点在直线上，则有 XeY－XYe＝0
２．由偏差方程确定加工动点引起的偏 差符号（若要计算偏差量，则偏差方程系数不能简 化）。
３．下一步插补方向确定原则：向使加 工偏差减小、并趋向轨迹终点的方向插补
．（将偏差等于零的情况并入偏差大于零的情况）。
４．关于插补量：每次插补一个脉冲当 量的位移
12
3. 圆弧插补
在圆弧加工过程中，可用动点到圆心的距离来描述刀具位置与 被加工圆弧之间关系。
b) 逆圆弧
图3-9 第一象限顺、逆圆弧
14
偏差递推简化：对第一象限顺圆，Fi≥0，动点Pi(Xi，Yi)应 向－Y向进给，新的动点坐标为(Xi＋1,Yi＋1)，且Xi＋1＝Xi，Yi ＋1＝Yi－1，则新点的偏差值为：
15
若Fi<0时，沿＋X向前进一步，到达（Xi＋1，Yi）点，新点

逐点比较法第一象限直线，圆弧插补编程逐点比较法是以折线来逼近给定的轨迹，就是每走一步控制系统都要将加工点与给定的图形轨迹相比较，以决定下一步进给的方向，使之逼近加工轨迹。

逐点比较法以折线来逼近直线或圆弧，其最大的偏差不超过一个最小设定单位。

只要将脉冲当量取得足够小，就可以达到精度要求。

逐点比较插补法在脉冲当量为0.01mm，系统进给速度小于3000mm/min时，能很好的满足要求。

一、逐点比较法直线插补如下图所示设直线 oA 为第一象限的直线，起点为坐标原点o (0 ， 0) ，终点坐标为， A( ) ， P() 为加工点。

若 P 点正好处在直线 oA 上，由相似三角形关系则有即点在直线 oA 上方 ( 严格为直线 oA 与 y 轴正向所包围的区域 ) ，则有即若 P 点在直线 oA 下方 ( 严格为直线 oA 与 x 轴正向所包围的区域 ) ，则有图 3 — 1 逐点比较法第一象限直线插补即令则有：①如，则点 P 在直线 oA 上，既可向 +x 方向进给一步，也可向 +y 方向进给一步；②如，则点 P 在直线 oA 上方，应向 +x 方向进给一步，以逼近oA 直线；③如，则点 P 在直线 oA 下方，应向 +y 方向进给一步，以逼近 oA 直线一般将及视为一类情况，即时，都向 +x 方向进给一步。

当两方向所走的步数与终点坐标相等时，停止插补。

这即逐点比较法直线插补的原理。

对第一象限直线 oA 从起点 ( 即坐标原点 ) 出发，当 F 时， +x 向走一步；当 F<0 时，y 向走一步。

特点：每一步都需计算偏差，这样的计算比较麻烦。

递推的方法计算偏差：每走一步后新的加工点的偏差用前一点的加工偏差递推出来。

采用递推方法，必须知道开始加工点的偏差，而开始加工点正是直线的起点，故。

下面推导其递推公式。

设在加工点 P( ) 处，，则应沿 +x 方向进给一步，此时新加工点的坐标值为新加工点的偏差为即若在加工点 P( ) 处，，则应沿 +y 方向进给一步，此时新加工点的坐标值为，新加工点的偏差为即综上所述，逐点比较法直线插补每走一步都要完成四个步骤 ( 节拍 ) ，即：(1) 位置判别根据偏差值大于零、等于零、小于零确定当前加工点的位置。

图5-10 脉冲增量差补流程框图
机电工程学院
２. 圆弧插补
在圆弧加工过程中，可用动点到圆心的距离来描述刀具位置与被加工 圆弧之间关系。设圆弧圆心在坐标原点，已知圆弧起点A（Xa，Ya），终 点B（Xb，Yb），圆弧半径为R。加工点可能在三种情况出现，即圆弧上、 圆弧外、圆弧内。当动点P（X，Y）位于圆弧上时有
机电工程学院
进给后新点的偏差计算公式除与前一点偏差 值有关外，还与动点坐标有关，动点坐标值随着 插补的进行是变化的，所以在圆弧插补的同时， 还必须修正新的动点坐标。
圆弧插补终点判别：将X、Y轴走的步数总和 存入一个计数器，N＝∣Xb－Xa∣＋∣Yb－Ya∣， 每走一步N减一，当N＝0发出停止信上方，如点P1，应向＋X向进给。 F<0时， 表示动点在OE下方，如点P2，应向＋Y向进给。 这里规定动点在直线上时，可归入F>0的情况一同考虑。
插补工作从起点开始，走一步，算一步, 判别一次，再走一步，
当沿两个坐标方向走的步数分别等于Xe和Ye时，停止插补。 下面将F的运算采用递推算法于以简化，动点Pi(Xi，Yi)的Fi值为：
Y 终点判别
N=7
N=6
3
N=5
N=4
2
N=3
N=2
1
N=1
N=0
O
E(4,3)
1 2 34
X
图5-7 直线插补轨迹过程实例
机电工程学院
例5-1 设加工第一象限直线OA，起点为坐标原点O（0，0），终点为A （6,4），试用逐点比较法对其进行插补，并画出插补轨迹。
插补从直线的起点开始，故F0，0=0；终点判别寄存器E存入X和Y两个 坐标方向的总步数，即E＝6＋4=10，每进给一步减1，E=0时停止插补。 插补运算过程如表5-1所示，插补轨迹如图所示。

-、逐点比较法1、直线L1：起点坐标O (0, 0),终点坐标A (4, 6)(1)分析1)直线L1为第一象限内直线2)插补总步数：M=x e+y e=4+6=103)若偏差任0,则刀具向+A x方向进给一步，偏差f i+1j = f.. - y e4)若偏差f<0,则刀具向+A y方向进给一步，偏差f. .+1= f.. + x e(2)列表计算(3)2、直线L2：起点坐标O (0, 0),终点坐标A (-6, 3)(1)分析1)直线L2为第二象限内直线2)插补总步数：M=l x e l+y e=6+3=93)若偏差任0,则刀具向-A x方向进给一步，偏差f i+1j = f.. - y e4)若偏差f<0,则刀具向+A y方向进给一步，偏差f, .+1= f.. +lx e\ (2)(3)3、直线L3：起点坐标O (0, 0),终点坐标A (-5, -8)(1)分析1)直线L3为第三象限内直线2)插补总步数：M=l x e l+l y e l=5+8=133)若偏差任0,则刀具向-A x方向进给一步，偏差f，+1. = f.. -\y\4)若偏差f<0,则刀具向-A y方向进给一步，偏差f,，+1 = f.. +\x\(2)列表计算(3)绘制进给脉冲图(略)4、直线L4：起点坐标O (0, 0),终点坐标A (7, -4)(1)分析1)直线L4为第四象限内直线2)插补总步数：M=x+\y\=7+4=113)若偏差任0,则刀具向+A x方向进给一步，偏差f i+1j = f.. -\y\4)若偏差f<0,则刀具向-A y方向进给一步，偏差f. .+1= f.. + x e(2)(3)5、圆弧NR1：起点坐标A (4, 0),终点坐标E (0, 4)(1)分析1)圆弧NR1为第一象限逆圆2)插补总步数：M=\(x0-x e)\+\(y0-y e)\=4+4=83)若偏差任0,则刀具向-A x方向进给一步，偏差f，+1 . = f.. ~2x. + 14)若偏差f<0,则刀具向+A y方向进给一步，偏差f, .+1 = f.. + 2y.+ 1 (2)列表计算(3)绘制进给脉冲图(略)6、圆弧NR2：起点坐标A (0, 5),终点坐标E (-5, 0)(1)分析1)圆弧NR2为第二象限逆圆2)插补总步数：M=l(x0-x e)l+l(j0-j e)l=5+5=103)若偏差任0,则刀具向-颂方向进给一步，偏差f.，+1 = f.. - 2y.+ 14)若偏差f<0,则刀具向-A x方向进给一步，偏差f，+1 . = f.. ~2x. + 1 (2)列表计算(3)绘制进给脉冲图(略)7、圆弧NR3：起点坐标A (-6, 0),终点坐标E (0, -6)(1)分析1)圆弧NR3为第三象限逆圆2)插补总步数：M=l(x0-x g)l+l(y0-y g)l=6+6=123)若偏差任0,则刀具向+A x方向进给一步，偏差f i+1j = f.. + 2x. + 14)若偏差f<0,则刀具向-A y方向进给一步，偏差f. .+1 = f.. - 2y. + 1 (2)列表计算(3)8、圆弧NR4：起点坐标A (0, -7),终点坐标E (7, 0)1)圆弧NR4为第四象限逆圆2)插补总步数：M=\(x Q-x e)\+\(y Q-y e)\=7+7=143)若偏差任0，则刀具向+A y方向进给一步，偏差f.，+1 =f.. + 2y.+ 14)若偏差f<0,则刀具向+A x方向进给一步，偏差f i+1j =加+ 2x. + 1(2)(3)9、圆弧SR1：起点坐标A (0, 4),终点坐标E (4, 0)(1)分析1)圆弧SR1为第一象限顺圆2)插补总步数：M=\(x0-x e)\+\(y0-y e)\=4+4=83)若偏差f N0,则刀具向-A y方向进给一步，偏差f, .+1 = f.. ~2y.+ 14)若偏差f<0，则刀具向+A x方向进给一步，偏差f.+1. = f.. + 2x. + 1(2)(3)绘制进给脉冲图(略)10、圆弧SR2：起点坐标A (-5，0)，终点坐标E (0，5)(1)分析1)圆弧SR2为第二象限顺圆2)插补总步数：M=\(x0-x e)\+\(y0-y e)\=5+5=103)若偏差f N0，则刀具向+A x方向进给一步，偏差f，+1. = f.. + 2x. + 14)若偏差f<0，则刀具向+A y方向进给一步，偏差f, .+1 = f.. + 2y.+ 1 (2)列表计算(3)绘制进给脉冲图(略)11、圆弧SR3：起点坐标A (0, -6),终点坐标E (-6, 0)(1)分析1)圆弧SR3为第三象限顺圆2)插补总步数：M=l(x0-x e)l+l(y0-y e)l=6+6=123)若偏差任0，则刀具向+颂方向进给一步，偏差f i+1j = f,. + 2y.+ 14)+1= "j - 2x.+ 1 (2)列表计算(3)12、圆弧SR4：起点坐标A (7, 0),终点坐标E (0, -7)(1)分析1)圆弧SR4为第四象限顺圆2)插补总步数：M=l(x0-x e)l+l(y0-y e)l=7+7=143)若偏差任0,则刀具向-A x方向进给一步，偏差f. .+1 = f.j - 2x. + 14)+1.（3二、数值积分法（DDA）1、直线L1：起点坐标O （0, 0）,终点坐标A （4, 6）（1）分析1）直线L1为第一象限内直线2）x e=4=100B；y e=6=110B3）取积分累加器容量N=3位4）x被积函数寄存器J vx= x e；y被积函数寄存器J vy= y e5）初始时：x累加器J Rx= 0；y累加器J Ry= 06）当J Rx累加超过3位溢出时，则在x方向分配一进给脉冲+A x7）当J Ry累加超过3位溢出时，则在y方向分配一进给脉冲+颂（2）列表计算:（3）绘制进给脉冲图（略）2、直线L2：起点坐标O（0，0），终点坐标A（-6，3）（1）分析1）直线L2为第二象限内直线2）x e=l-6l=110B；y e=3=011B3）取积分累加器容量N=3位4）x被积函数寄存器J vx= x e；y被积函数寄存器J vy= y e5）初始时：x累加器J Rx= 0；y累加器J Ry= 06）当J Rx累加超过3位溢出时，则在x方向分配一进给脉冲-A x 7）当J Ry累加超过3位溢出时，则在y方向分配一进给脉冲+A y （2）列表计算二进制累加：累加N3）：累加（3）绘制进给脉冲图（略）3、直线L3：起点坐标O（0，0），终点坐标A（-5，-8）（1）分析1）直线L3为第三象限内直线2）x e=|-5|=101B；y e=|-8|=1000B3）取积分累加器容量N=4位4）x被积函数寄存器J vx= x e；y被积函数寄存器J vy= y e5）初始时：x累加器J Rx= 0；y累加器J Ry= 06）当J Rx累加超过4位溢出时，则在x方向分配一进给脉冲-A x 7）当J Ry累加超过4位溢出时，则在y方向分配一进给脉冲-A y （2）列表计算二进制累加：（3）绘制进给脉冲图（略）4、直线L4：起点坐标O （0, 0）,终点坐标A （7, -4）（1）分析1）直线L4为第四象限内直线2）x e=7=111B；y e=l-4l=100B3）取积分累加器容量N=3位4）x被积函数寄存器J vx= x e；j被积函数寄存器J vy= y e5）初始时：x累加器J Rx= 0；j累加器J Ry= 06）当J Rx累加超过3位溢出时，则在x方向分配一进给脉冲+A x 7）当J Ry累加超过3位溢出时，则在j方向分配一进给脉冲-颂（2）列表计算二进制累加：N3）：（3）绘制进给脉冲图（略）5、圆弧NR1：起点坐标A （4, 0）,终点坐标E （0, 4）（1）分析1）圆弧NR1为第一象限逆圆2）x0=4=100B；y0=0=000B3）取积分累加器容量N=3位4）初始时：x被积函数寄存器J vx= y0；y被积函数寄存器J vy= x05）初始时：x累加器J Rx= 0；y累加器J Ry= 06）当J Rx累加超过3位溢出时，则在x方向分配一进给脉冲-A x，相应在J vy中对x 坐标的修正为减一7）当J Ry累加超过3位溢出时，则在y方向分配一进给脉冲+A y，相应在J vx中对y 坐标的修正为加一（2）列表计算（3）绘制进给脉冲图（略）7、圆弧NR3：起点坐标A （-6, 0）,终点坐标E （0, -6）（1）分析1） 圆弧NR3为第三象限逆圆 2） 扁=I-6I=110B ； y 0=0=000B 3） 取积分累加器容量N=3位4） 初始时：x 被积函数寄存器J vx = y 0； y 被积函数寄存器J vy = x 0 5） 初始时：x 累加器J Rx = 0； y 累加器J Ry = 06） 当J Rx 累加超过3位溢出时，则在x 方向分配一进给脉冲+A x ，相应在J vy 中对x 坐标的修正为减一7） 当J Ry 累加超过3位溢出时，则在y 方向分配一进给脉冲-颂，相应在J vx 中对y坐标的修正为加一（2）列表计算_8_ 9 10 11 12 1314(-44) (-4,4) (-5,3) (-5,3)(-3+4=7 7+4=11 (3)停止累加2+4=6 6+4=10(2) 2+5=7 7+5=12(4) 4+6=10(2) 2+6=8(0)停止累加0 1 0 1 1 1 0(3) 绘制进给脉冲图(略)8、圆弧NR4：起点坐标A （0, -7）,终点坐标E （7, 0）（1）分析1） 圆弧NR4为第四象限逆圆 8） x 0=0=000B ； j 0=|-7l=111B 9） 取积分累加器容量N=3位10） 初始时：x 被积函数寄存器J vx = y 0； y 被积函数寄存器J vy = x 0 11） 初始时：x 累加器J Rx = 0； y 累加器J Ry = 012） 当J Rx 累加超过3位溢出时，则在x 方向分配一进给脉冲+A x ，相应在J vy 中对 x 坐标的修正为加一2） 当J Ry 累加超过3位溢出时，则在y 方向分配一进给脉冲+A y ，相应在J vx 中对y 坐标的修正为减一（2）列表计算10 11 12 13 14 15(-4,-6) (-3,-6) (-2,-6) (-1,-7+6=13(5) 5+6=11(3) 3+6=9 (1) 1+6=7 7+6=13 (5)停止累加1 1 1 0 1 0停止累加（3）绘制进给脉冲图（略）9、圆弧SR1：起点坐标A （0, 4）,终点坐标E （4, 0）（1）分析1） 圆弧SR1为第一象限顺圆 2） x 0=0=000B ； j 0=4=100B 3） 取积分累加器容量N=3位4） 初始时：x 被积函数寄存器J vx = y 0； y 被积函数寄存器J vy = x 0 5） 初始时：x 累加器J Rx = 0； y 累加器J Ry = 06） 当J Rx 累加超过3位溢出时，则在x 方向分配一进给脉冲+A x ,相应在J vy 中对x坐标的修正为加一7） 当J Ry 累加超过3位溢出时，则在y 方向分配一进给脉冲-颂，相应在J vx 中对y坐标的修正为减一（2）列表计算11 12 13 1415(7, -4) (7, - 3) (7, - 2)-6+5=11⑶3+7=10(2) 2+7=9(1) 1+7=8(0) 0+7=7 7+7=14(6)停止累加1 1 0 1 0（3）绘制进给脉冲图（略）10、圆弧SR2：起点坐标A （-5, 0）,终点坐标E （0, 5）（1）分析1）圆弧SR2为第二象限顺圆 2） x 0=l-5l=101B ； j 0=0=000B 3） 取积分累加器容量N=3位4） 初始时：x 被积函数寄存器J vx = y 0； y 被积函数寄存器J vy = x 0 5） 初始时：x 累加器J Rx = 0； y 累加器J Ry = 06） 当J Rx 累加超过3位溢出时，则在x 方向分配一进给脉冲+A x ，相应在J vy 中对x 坐标的修正为减一7） 当J Ry 累加超过3位溢出时，则在y 方向分配一进给脉冲+A y ，相应在J vx 中对y 坐标的修正为加一（2）列表计算12 13 1415(4,2)g (41) (4,1) (4,0)3+4=7 7+4=11(3) 3+4=7 7+4=11(3)停止累加1 0 1 0（3）绘制进给脉冲图（略）11、圆弧SR3：起点坐标A （0, -6）,终点坐标E （-6, 0）（1）分析1）圆弧SR3为第三象限顺圆 2） x 0=0=000B ； y 0=l-6l=110B 3） 取积分累加器容量N=3位4） 初始时：x 被积函数寄存器J vx = y 0； y 被积函数寄存器J vy = x 0 5） 初始时：x 累加器J Rx = 0； y 累加器J Ry = 06） 当J Rx 累加超过3位溢出时，则在x 方向分配一进给脉冲-A x ，相应在J vy 中对x 坐标的修正为加一7） 当J Ry 累加超过3位溢出时，则在y 方向分配一进给脉冲+A y ，相应在J vx 中对y 坐标的修正为减一（2）列表计算141514(-6,-1)15(-6,0)停止累加0（3）绘制进给脉冲图（略）12、圆弧SR4：起点坐标A （7, 0）,终点坐标E （0, -7）（1）分析1）圆弧SR4为第四象限顺圆2）x0=7=111B；j0=0=000B3）取积分累加器容量N=3位4）初始时：x被积函数寄存器J vx= y0；y被积函数寄存器J vy= x05）初始时：x累加器J Rx= 0；y累加器J Ry= 06）当J Rx累加超过3位溢出时，则在x方向分配一进给脉冲-A x，相应在J vy中对x 坐标的修正为减一7）当J Ry累加超过3位溢出时，则在y方向分配一进给脉冲-A y，相应在J vx中对y 坐标的修正为加一（2）列表计算(3)绘制进给脉冲图(略)。

y L2 F0 F<0 F<0 F0 L3
四象限直线偏差符号和进给方向
L1 F0 F<0 x F<0 F0 L4
由图可见，靠近Y轴区域偏差大等于零，靠近X轴区域偏差小于零。F≥0时，进 给都是沿X轴，不管是＋X向还是－X向，X的绝对值增大；F<0时，进给都是沿Y轴， 不论＋Y向还是－Y向，Y的绝对值增大。
v y 60f y
式中 δ—脉冲当量（mm/脉冲）。合成进给速度为
v v x 2 v y 2 60 f x2 f y2
若fx=0或fy=0时，也就是刀具沿平行于坐标轴的方向切削，这时对 应轴切削速度最大
第四章 插补原理
3.1 数字积分法的基本原理
第 三 节 数 字 积 分 法
F5 F4 2Y4 1 3 F6 F5 2 X 5 1 4
F7 F6 2Y6 1 1
F8 F7 2Y7 1 0
5. 四个象限中圆弧插补 第一象限逆圆弧CD：即Fi≥0时，走—X轴， 动点的偏差函数为
Fi 1＝Fi 2 X i 1
第四章 插补原理
2.3 逐点比较法圆弧插补
第 二 节 逐 点 比 较 法
第一象限圆弧插补 流程图
例3 现欲加工第一象限顺圆弧AB，如图所示，起点A（0，4），终点B（4，0）， 试用逐点比较法进行插补。
Y 4 3 2 1 B(4,0) O 1 2 3 4 X A(0,4)
表3 圆弧插补过程
步数 起点 偏差判别 坐标进给 偏差计算 坐标计算 终点判别
如图4-14所示，从t=0时
刻到t时刻，函数y=f（t） 曲线所包围的面积可表示
Y
Y=f(t)
YO

§2—1 逐点比较法逐点比较法是我国数控机床中广泛采用的一种插补方法，它能实现直线、圆弧和非圆二次曲线的插补，插补精度较高。

逐点比较法，顾名思义，就是每走一步都要将加工点的瞬时坐标同规定的图形轨迹相比较，判断其偏差，然后决定下一步的走向，如果加工点走到图形外面去了，那么下一步就要向图形里面走；如果加工点在图形里面，那么下一步就要向图形外面走，以缩小偏差。

这样就能得出一个非常接近规定图形的轨迹，最大偏差不超过一个脉冲当量。

在逐点比较法中，每进给一步都须要进行偏差判别、坐标进给、新偏差计算和终点比较四个节拍。

下面分别介绍逐点比较法直线插补和圆弧插补的原理。

一、 逐点比较法直线插补如上所述，偏差计算是逐点比较法关键的一步。

下面以第Ⅰ象限直线为例导出其偏差计算公式。

图 2-1 直 线 差 补 过 程e )OY图2-1 直线插补过程点击进入动画观看逐点比较法直线插补如图2—1所示，假定直线 OA 的起点为坐标原点，终点A 的坐标为e e i j A(x ,y ),P(x ,y )为加工点，若P 点正好处在直线OA 上，那么下式成立：e j i e x y - x y 0若任意点i j P(x ,y )在直线 OA 的上方（严格地说，在直线OA 与y 轴所成夹角区域内），那么有下述关系成立：jei ey y x x >亦即:e j i e x y - x y 0>由此可以取偏差判别函数ij F 为：ij e j i e F x y - x y ＝由 ij F 的数值（称为“偏差”）就可以判别出P 点与直线的相对位置。

即： 当 ij F =0时，点i j P(x ,y )正好落在直线上；当 ij F >0时，点i j P(x ,y )落在直线的上方；当ij F <0时，点i j P(x ,y )落在直线的下方。

从图2—1看出，对于起点在原点，终点为A （ e e x ,y ）的第Ⅰ象限直线OA 来说，当点P 在直线上方（即ij F >0）时，应该向+x 方向发一个脉冲，使机床刀具向+x 方向前进一步，以接近该直线；当点P 在直线下方（即ij F <0）时，应该向+y 方向发一个脉冲，使机床刀具向+y 方向前进一步，趋向该直线；当点P 正好在直线上（即 ij F =0）时，既可向+x 方向发一脉冲，也可向+y 方向发一脉冲。

所以，第一象限逆时针圆弧插补加工时偏差加工的递推 公式为： Fi+1 = Fi－2Xi + 1 （ Fi≥0时） Fi+1 = Fi + 2Yi + 1 （Fi＜0时）
同理，对于第一象限顺圆加工时，即B→A，当Fi≥0时， 应向－Y方向进给一步，当Fi＜0时，应向+X方向进给 一步。
Y
B(Xe,Ye) Pi(Xi,Yi) A(Xo,Yo)
所以，第一象限顺时针圆弧插补加工时偏差加工的递推 公式为： Fi+1 = Fi－2Yi + 1 （ Fi≥0时） Fi+1 = Fi + 2Xi + 1 （Fi＜0时）
（4）终点判别 1）根据X、Y坐标方向要走的总步数∑来判断，即∑=lXeXol +lYe -Yol,每走一步进行∑－1计算，当∑=0时即到 终点。 2）分别判断各坐标轴的步数,∑x=lXe-Xol ， ∑y= lYe –Yol，当沿坐标值方向进给一步时进行∑－1计算， 当∑x=0 ，∑y=0时即到终点。
F6=F5-2X5+1 =0, X6=0,Y5=3
偏差计算 F0=0,Xo=3,Yo=0
终点判别
∑=0
加工过程为： Y 3 2
B
1
O A
1
2
3
X
习题：设圆弧AB为第一象限逆圆弧，起点A（５，0）,终 点为B（0,５），用逐点比较法加工圆弧AB。 Y 5 4 3 2 1 O
1
2
3ห้องสมุดไป่ตู้
4
5
X
运算过程：
O
X
O
X
当Fi≥0时，向－Y方向进给一步，动点由Pi(Xi,Yi) 移动到 Pi+1(Xi,Yi +1)，则新动点的坐标为 Yi+1=Yi －１ 代入偏差函数，得Pi+1点的偏差为： Fi+1 = Fi－2Yi + 1 当Fi＜0时，向+X方向进给一步，动点由Pi(Xi,Yi) 移动到 Pi+1(Xi +1,Yi)，则新动点的坐标为 Xi+1=Xi +１ 代入偏差函数，得Pi+1点的偏差为： Fi+1 = Fi + 2Xi + 1

3.逐点比较法圆弧插补 3.逐点比较法圆弧插补
（1）偏差函数 任意加工点P ），偏差函数 偏差函数F 任意加工点Pi（Xi，Yi），偏差函数Fi可表示为
Fi = X i2 + Yi 2 − R 2
=0，表示加工点位于圆上； 若Fi=0，表示加工点位于圆上； Y >0，表示加工点位于圆外； 若Fi>0，表示加工点位于圆外； <0， 若Fi<0，表示加工点位于圆内
Y Ae (Xe,Ye) F>0 Pi (Xi,Yi) F<0 X
为便于计算机计算) （2）偏差函数字的递推计算 (为便于计算机计算 为便于计算机计算 >=0，规定向+ 方向走一步（若坐标单位用脉冲当量表示） 若Fi>=0，规定向+X方向走一步（若坐标单位用脉冲当量表示）
Xi+1 = Xi +1 Fi+1 = XeYi −Ye (Xi +1) = Fi −Ye
2.逐点比较法直线插补 2.逐点比较法直线插补
（1）偏差函数构造 对于第一象限直线OA上任一点( OA上任一点 对于第一象限直线OA上任一点(X,Y) YX e − XYe = 0 若刀具加工点为Pi（ ），则该点的偏差 若刀具加工点为Pi（Xi，Yi），则该点的偏差 Pi 函数F 函数Fi可表示为 Fi = Yi X e − X i Ye 若Fi=0，表示加工点位于直线上； 表示加工点位于直线上； 表示加工点位于直线上方； 若Fi>0，表示加工点位于直线上方； 表示加工点位于直线下方。 若Fi<0，表示加工点位于直线下方。
F=0 F<0 F>0 F<0 F>0 F=0 F<0 F>0 F<0 F>0

+XF方i 向0走一步，到达新加工点，即：
xi xi 1
若 Fi，1 则向yYi 轴xe发出(一xi个进1给) y脉e冲，F刀i 具从y该e 点向
+YF方i 向0走一步，到达新加工点，即：
yi1 yi 1
Fi1 ( yi 1)xe xi ye Fi xe
第2章 直线插补原理
由此得出递推公式（ ☺重点掌握☺）
① 偏差判别：根据偏差判断应该向哪个坐标方向 进给；
② 坐标进给：根据判别结果，沿相应的坐标方向 进给；
③ 新偏差计算：根据偏差函数，计算进给后的偏 差，作为下次偏差判别的依据；
④ 终点比较：判断是否达到终点，若达到终点则 结束本次插补程序，否则转①继续执行。
第2章 直线插补原理
2.2.3 逐点比较法的特点
逐点比较法的关键是找出容易计算的偏差函数 （直线、圆弧、抛物线、螺旋线等），然后再 比较误差。
逐点比较法运算直观，插补误差不大于一个脉 冲当量。
逐点比较法是我国数控机床中广泛采用的一种 插补方法，它能实现直线、圆弧和非圆二次曲 线的插补，插补精度较高。
第2章 直线插补原理
2.2.3 逐点比较法直线插补原理
——根据给定的信息进行数字计算，在计算过 程中不断向各个坐标发出相互协调的进给脉冲， 使被控机械部件按指定的路线移动。
2.1.3 插补要解决的问题
让单独的坐标分别运动合成理想的轨迹，还是几个坐 标同时进给？
判断往哪一个坐标方向进给，使下一步误差更小？ 进给多少？
第2章 直线插补原理
如果同时进给？
偏差函数的递推计算（第一象限为例）
若 Fi 0 ，规定向-X方向走一步：
xi1 xi 1
Fi1
(xi

数控机床DDA数字积分法插补第⼀象限直线,逐点⽐较法插补⼆三象限顺圆弧⽬录⼀、课程设计介绍1.1 任务说明 (3)1.2要求 (3)⼆、程序操作及算法流程图2.1 DDA法插补直线流程 (3)2.2逐点⽐较法插补逆时针圆弧流程 (4)三、⽤户使⽤说明3.1 程序开始运⾏时显⽰介⾯ (5)3.2 执⾏计算 (5)3.3 DDA法直线插补实例 (6)3.4 逐点⽐较法插补第⼆三象限逆时针圆弧 (7)四、主要算法及源程序4.1 程序设计概述 (8)4.2 主要算法的实现 (8)4.2.1 参数声明 (8)4.2.2复位操作 (9)4.2.3单步操作 (11)4.2.4 连续插补 (11)4.2.5 辅助操作 (13)五、本设计的特点 (13)六、课程设计的感想 (13)七、主要参考⽂献 (14)⼀、课程设计介绍1.1、任务说明：（1）直线插补：DL1, DDA 法第⼀象限直线插补。

（2）圆弧插补：PA23，逐点⽐较法⼆三象限顺圆弧插补。

1.2、要求：（1）具有数据输⼊界⾯，如：起点，终点，圆⼼，半径及插补步长。

（2）具有插补过程的动态显⽰功能，如：但单步插补，连续插补，插补步长可调。

本课程设计的题⽬要求是ＤＤＡ数字积分法插补第⼀象限直线,逐点⽐较法插补⼆三象限顺圆弧。

由于本课设要求只为⼆三象限，故默认为劣弧插补。

此外，对于两种插补对象均可根据需要改变插补步长，以表现不同的插补效果。

在插补显⽰过程中，有两种插补显⽰⽅式，即⼿动单步插补和⾃动连续插补动态显⽰。

⼆、程序操作及算法流程图 2.1 DDA 法插补直线流程初始化sx sy ex ey 步长bc 寄存器vx1 vy1 累加器 rx1 ry1rx1=rx1+vx1 ry1=ry1+vy1ry1是否溢出rx1是否溢出是否到达终点结束 +x ⾛⼀个步长 +y ⾛⼀个步长NY NYNY开始DDA 插补第⼀象限的直线流程图2.2逐点⽐较法插补逆时针圆弧流程逐点⽐较法插补⼆三象限逆圆弧参数说明：sx 、sy 为起点坐标ex 、ey 为终点坐标开始初始化sx ex sy sy bc 弧半径平⽅rY21>=0r>=0r>=0向—y ⾛⼀步向x ⾛⼀步向—y ⾛⼀步向—x ⾛⼀步是否到达终点结束yyynnnn yn为进给总次数cx、cy为圆⼼坐标bc为步长m为寄存器位数s_1表⽰按下直线选项，s_2表⽰按下圆弧按钮三、⽤户使⽤说明——软件运⾏说明及结果显⽰3.1 程序开始运⾏时显⽰介⾯3.2 执⾏计算在右侧⾯板中有参数输⼊区，⽅式选择区以及执⾏按钮等操作。