逐点比较法直线插补资料讲解

实验二一、内容实验二逐点比较法插补实验二、重点/难点内容实验装置和实验环境的熟悉和了解；逐点比较法插补算法的实现；逐点比较法插补的过象限处理；实验中碰到的疑难问题分析和改进。

三、详细内容（一）实验目的1．进一步掌握“数控原理与系统实验装置”的使用方法；2．掌握逐点比较法直线插补和圆弧插补的基本工作原理和软件实现方法。

（二）实验器材1．计算机一台；2．数控原理与系统实验装置一套；3．C语言支持软件。

（三）预习要求1．复习教材中有关“逐点比较法插补”的有关内容；2．仔细阅读本实验指导书前言部分内容，要求完全掌握实验装置的使用；3．仔细阅读本实验内容和提供的部分参考程序清单。

（四）实验原理逐点比较法是使用阶梯折线来逼近被插补直线或圆弧轮廓的方法，一般是按偏差判别、进给控制、偏差计算和终点判别共四个节拍来实现一次插补过程。

根据教材中有关内容，给出第一象限内直线与圆弧的逐点比较法插补的流程图如教材中图3-5和图3-8所示。

当插补过程中某个坐标轴出现进给脉冲时，可通过调用开环系统的位置控制函数来完成，具体如下：void open_position_ctrl (int Dx, int Dy)；其中，Dx = +1、-1、0，分别表示X轴方向上出现正向进给脉冲、反向进给脉冲、没有进给脉冲。

Dy=+1、-1、0，分别表示Y轴方向上出现正向进给脉冲、反向进给脉冲、没有进给脉冲。

在将进给脉冲送给小型铣床执行的同时，也可通过CRT来模拟显示插补轨迹，以便观察插补过程的正确性。

为了简单起见，本次实验过程中只要求实现L1和NR1的插补。

（五）参考程序清单见实验教材《数控系统综合实践》所附光盘。

（六）实验步骤1．启动C语言编辑环境，打开实验程序文件（exp03.cpp）；2．输入预先编好的部分程序；3．调试程序，并通过CRT模拟显示，验证其正确性。

(*) 调试过程中不开功放电源。

4．在模拟成功后，增加位置控制输出程序，并打开功放电源，利用小型铣床画出被插补的结果。

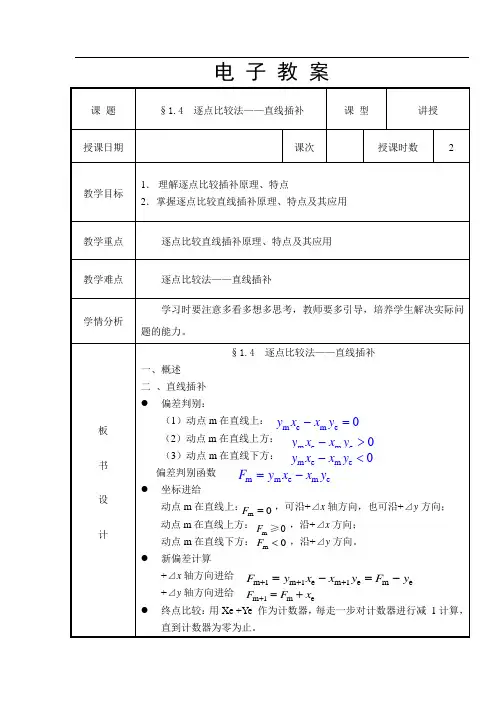
电子教案教学程序教学内容及教学双边活动与教学方法导入新课讲授探究总结在刀具按要求轨迹运动加工零件轮廓的过程中，不断比较刀具与被加工零件轮廓之间的相对位置，并根据比较结果决定下一步的进给方向，使刀具向减小误差的方向进给。

其算法最大偏差不会超过一个脉冲当量δ。

§1.4 逐点比较法——直线插补一、概述初称区域判别法，又称代数运算法或醉步式近似法。

这种方法应用广泛，能实现平面直线、圆弧、二次曲线插补，精度高。

每进给一步需要四个节拍：（1）偏差判别：判别加工点对规定图形的偏离位置，决定拖板进给的走向。

（2）坐标进给：控制某个坐标工作台进给一步，向规定的图形靠拢，缩小偏差。

（3）偏差计算：计算新的加工点对规定图形的偏差，作为下一步判别的依据。

（4）终点判断：判断是否到达终点。

若到达则停止插补，若没，再回到第一节拍。

介绍讲授图示分析讲授法理解记忆教学程序教学内容及教学双边活动与教学方法新课讲授探究总结二、直线插补1．偏差计算公式如图所示第一象限直线OA，起点O为坐标原点，编程时，给出直线的终点坐标A ，直线方程为：●偏差判别：（1）动点m在直线上：（2）动点m在直线上方：（3）动点m在直线下方：偏差判别函数●坐标进给（1）动点m在直线上：，可沿+⊿x轴方向，也可沿+⊿y方向；（2）动点m在直线上方：，沿+⊿x方向；（3）动点m在直线下方：，沿+⊿y方向。

举例板图分析总结e e(,)x ym e m ey x x y-=m e m ey x x y-=m e m ey x x y->m e m ey x x y-<m m e m eF y x x y=-mF<mF≥mF=教学程序教学内容及教学双边活动与教学方法探究总结例题讲授●新偏差计算+⊿x轴方向进给+⊿y轴方向进给●终点比较用Xe +Ye 作为计数器，每走一步对计数器进行减1计算，直到计数器为零为止。

2．终点判别法分别计数法双向计数法单向计数法3．插补运算过程插补计算时，每走一步，都要进行以下4个步骤（又称4个节拍）的算术运算或逻辑判断：方向判定：根据偏差值判定进给方向。

逐点比较法（代数运算法、醉步法）图解1、逐点比较法直线插补第Ⅰ象限一加工直线，起点坐标原点O，终点坐标为A（xe，ye），则直线方程可表示为，即令Fi，j=xeyj-yexi为偏差判别函数，则有：（1）当Fi，j≥0时，向＋X方向进给一个脉冲当量，到达点Pi＋1，j，此时xi＋1=xi＋1，则点Pi＋1，j的偏差判别函数Fi+1，j为（2）当Fi，j＜0时，向＋Y方向进给一个脉冲当量，到达点Pi，j ＋1，此时yj+1=yj＋1，则点Pi，j＋1的偏差判别函数Fi，j+1为可见，新加工点的偏差Fi+1，j或Fi，j+1是由前一个加工点的偏差Fi，j和终点的坐标值递推出来的，假如按前两式计算偏差，则计算大为简化。

终点判别三种方法：（1）判别插补或进给的总步数：N=Xe+Ye；（2）分别判别各坐标轴的进给步数；（3）仅推断进给步数较多的坐标轴的进给步数。

总结：第一拍判别其次拍判别第三拍判别第四拍比较Fij≥0+ΔxFi+1，j= Fi，j-yeEi+j=E终-1Fij0+ΔyFi，j+1= Fi，j+xe第Ⅰ象限直线插补流程图：例5-1 设加工第一象限直线，起点为坐标原点O（0，0），终点A （6，4），用逐点比较法对其进行插补，并画出插补轨迹。

终点判别寄存器E＝6＋4=10，每进给一步减1，E=0时停止插补。

步数偏差判别坐标进给偏差计算终点判别起点F0，0=0E=101F0，0=0＋XF1，0=F0，0－ye=0－4=－4 E=10－1=92F1，0＜0＋YF1，1= F1，0＋xe=－4＋6=2 E=9－1=83F1，1＞0＋XF2，1= F1，1－ye=2－4=－2 E=8－1=74F2，1＜0＋YF2，2= F2，1＋xe=－2＋6=4 E=7－1=65F2，2＞0＋XF3，2= F2，2－ye=4－4=0 E=6－1=56F3，2=0＋XF4，2= F3，2－ye=0－4=－4 E=5－1=47F4，2＜0＋YF4，3= F4，2＋xe=－4＋6=2 E=4－1=38F4，3＞0＋XF5，3= F4，3－ye=2－4=－2 E=3－1=29F5，3＜0＋YF5，4= F5，3＋xe=－2＋6=4E=2－1=110F5，4＞0＋XF6，4= F5，4－ye=4－4=0E=1－1=02、其他象限直线插补的方法：1）分别处理法分别建立其他三个象限偏差函数计算公式。

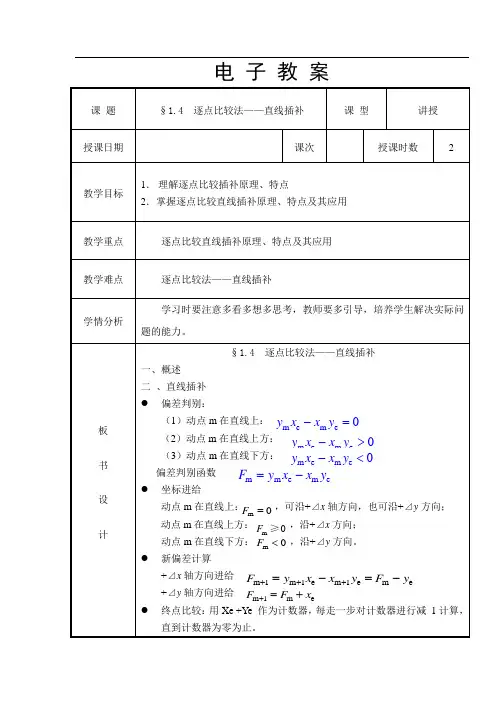
电子教案教学程序教学内容及教学双边活动与教学方法导入新课讲授探究总结在刀具按要求轨迹运动加工零件轮廓的过程中，不断比较刀具与被加工零件轮廓之间的相对位置，并根据比较结果决定下一步的进给方向，使刀具向减小误差的方向进给。

其算法最大偏差不会超过一个脉冲当量δ。

§1.4 逐点比较法——直线插补一、概述初称区域判别法，又称代数运算法或醉步式近似法。

这种方法应用广泛，能实现平面直线、圆弧、二次曲线插补，精度高。

每进给一步需要四个节拍：（1）偏差判别：判别加工点对规定图形的偏离位置，决定拖板进给的走向。

（2）坐标进给：控制某个坐标工作台进给一步，向规定的图形靠拢，缩小偏差。

（3）偏差计算：计算新的加工点对规定图形的偏差，作为下一步判别的依据。

（4）终点判断：判断是否到达终点。

若到达则停止插补，若没，再回到第一节拍。

介绍讲授图示分析讲授法理解记忆教学程序教学内容及教学双边活动与教学方法新课讲授探究总结二、直线插补1．偏差计算公式如图所示第一象限直线OA，起点O为坐标原点，编程时，给出直线的终点坐标A ，直线方程为：●偏差判别：（1）动点m在直线上：（2）动点m在直线上方：（3）动点m在直线下方：偏差判别函数●坐标进给（1）动点m在直线上：，可沿+⊿x轴方向，也可沿+⊿y方向；（2）动点m在直线上方：，沿+⊿x方向；（3）动点m在直线下方：，沿+⊿y方向。

举例板图分析总结e e(,)x ym e m ey x x y-=m e m ey x x y-=m e m ey x x y->m e m ey x x y-<m m e m eF y x x y=-mF<mF≥mF=教学程序教学内容及教学双边活动与教学方法探究总结例题讲授●新偏差计算+⊿x轴方向进给+⊿y轴方向进给●终点比较用Xe +Ye 作为计数器，每走一步对计数器进行减1计算，直到计数器为零为止。

2．终点判别法分别计数法双向计数法单向计数法3．插补运算过程插补计算时，每走一步，都要进行以下4个步骤（又称4个节拍）的算术运算或逻辑判断：方向判定：根据偏差值判定进给方向。

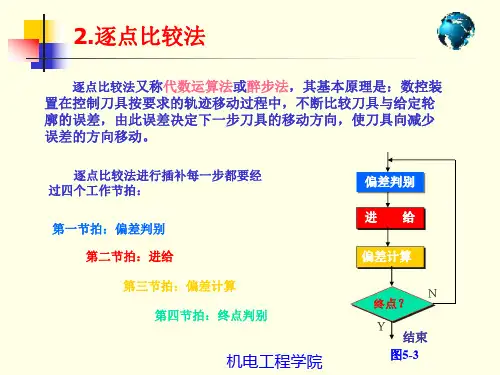
逐点比较法第一象限直线插补编程逐点比较法是以折线来逼近给定的轨迹，就是每走一步控制系统都要将加工点与给定的图形轨迹相比较，以决定下一步进给的方向，使之逼近加工轨迹。

逐点比较法以折线来逼近直线或圆弧，其最大的偏差不超过一个最小设定单位。

只要将脉冲当量取得足够小，就可以达到精度要求。

逐点比较插补法在脉冲当量为0.01mm，系统进给速度小于3000mm/min时，能很好的满足要求。

一、逐点比较法直线插补如下图所示设直线 oA 为第一象限的直线，起点为坐标原点o (0 ， 0) ，终点坐标为， A( ) ， P() 为加工点。

若 P 点正好处在直线 oA 上，由相似三角形关系则有即点在直线 oA 上方 ( 严格为直线 oA 与 y 轴正向所包围的区域 ) ，则有即若 P 点在直线 oA 下方 ( 严格为直线 oA 与 x 轴正向所包围的区域 ) ，则有图 3 — 1 逐点比较法第一象限直线插补即令则有：①如，则点 P 在直线 oA 上，既可向 +x 方向进给一步，也可向 +y 方向进给一步；②如，则点 P 在直线 oA 上方，应向 +x 方向进给一步，以逼近oA直线；③如，则点 P 在直线 oA 下方，应向 +y 方向进给一步，以逼近 oA直线一般将及视为一类情况，即时，都向 +x 方向进给一步。

当两方向所走的步数与终点坐标相等时，停止插补。

这即逐点比较法直线插补的原理。

对第一象限直线 oA 从起点 ( 即坐标原点 ) 出发，当 F时， +x 向走一步；当 F<0 时，y 向走一步。

特点：每一步都需计算偏差，这样的计算比较麻烦。

递推的方法计算偏差：每走一步后新的加工点的偏差用前一点的加工偏差递推出来。

采用递推方法，必须知道开始加工点的偏差，而开始加工点正是直线的起点，故。

下面推导其递推公式。

设在加工点 P( ) 处，，则应沿 +x 方向进给一步，此时新加工点的坐标值为新加工点的偏差为即若在加工点 P( ) 处，，则应沿 +y 方向进给一步，此时新加工点的坐标值为，新加工点的偏差为即综上所述，逐点比较法直线插补每走一步都要完成四个步骤 ( 节拍 ) ，即：(1) 位置判别根据偏差值大于零、等于零、小于零确定当前加工点的位置。

电子教案教学程序教学容及教学双边活动与教学方法导入新课讲授探究总结在刀具按要求轨迹运动加工零件轮廓的过程中，不断比较刀具与被加工零件轮廓之间的相对位置，并根据比较结果决定下一步的进给方向，使刀具向减小误差的方向进给。

其算法最大偏差不会超过一个脉冲当量δ。

§1.4 逐点比较法——直线插补一、概述初称区域判别法，又称代数运算法或醉步式近似法。

这种方法应用广泛，能实现平面直线、圆弧、二次曲线插补，精度高。

每进给一步需要四个节拍：（1）偏差判别：判别加工点对规定图形的偏离位置，决定拖板进给的走向。

（2）坐标进给：控制某个坐标工作台进给一步，向规定的图形靠拢，缩小偏差。

（3）偏差计算：计算新的加工点对规定图形的偏差，作为下一步判别的依据。

（4）终点判断：判断是否到达终点。

若到达则停止插补，若没，再回到第一节拍。

介绍讲授图示分析讲授法理解记忆教学程序教学容及教学双边活动与教学方法新课讲授探究总结二、直线插补1．偏差计算公式如图所示第一象限直线OA，起点O为坐标原点，编程时，给出直线的终点坐标A ，直线方程为：●偏差判别：（1）动点m在直线上：（2）动点m在直线上方：（3）动点m在直线下方：偏差判别函数●坐标进给（1）动点m在直线上：，可沿+⊿x轴方向，也可沿+⊿y方向；（2）动点m在直线上方：，沿+⊿x方向；（3）动点m在直线下方：，沿+⊿y方向。

举例板图分析总结e e(,)x ymF<mF≥mF=教学程序教学容及教学双边活动与教学方法探究总结例题讲授例题讲授●新偏差计算+⊿x轴方向进给+⊿y轴方向进给●终点比较用Xe +Ye 作为计数器，每走一步对计数器进行减1计算，直到计数器为零为止。

2．终点判别法分别计数法双向计数法单向计数法3．插补运算过程插补计算时，每走一步，都要进行以下4个步骤（又称4个节拍）的算术运算或逻辑判断：方向判定：根据偏差值判定进给方向。

坐标进给：根据判定的方向，向该坐标方向发一进给脉冲。

逐点比较法直线插补（1）偏差函数构造对于第一象限直线OA上任一点(X,Y:X/Y = Xe/Ye若刀具加工点为Pi（Xi，Yi），则该点的偏差函数Fi可表示为：若Fi= 0，表示加工点位于直线上；若Fi> 0，表示加工点位于直线上方；若Fi< 0，表示加工点位于直线下方。

（2）偏差函数字的递推计算采用偏差函数的递推式（迭代式）：既由前一点计算后一点Fi =Yi Xe -XiYe若Fi>=0，规定向 +X 方向走一步Xi+1 = Xi +1Fi+1 = XeYi –Ye(Xi +1=Fi –Ye若Fi<0，规定 +Y 方向走一步，则有Yi+1 = Yi +1Fi+1 = Xe(Yi +1-YeXi =Fi +Xe（3）终点判别直线插补的终点判别可采用三种方法。

1）判断插补或进给的总步数： 2）分别判断各坐标轴的进给步数；3）仅判断进给步数较多的坐标轴的进给步数。

（4）例对于第一象限直线OA，终点坐标Xe=6 ,Ye=4，插补从直线起点O开始，故F0=0 。

终点判别是判断进给总步数N=6+4=10，将其存入终点判别计数器中，每进给一步减1，若N=0，则停止插补。

逐点比较法圆弧插补（1）偏差函数构造任意加工点Pi（Xi，Yi），偏差函数Fi可表示为若Fi=0，表示加工点位于圆上；若Fi>0，表示加工点位于圆外；若Fi<0，表示加工点位于圆内（2）偏差函数的递推计算1）逆圆插补若F≥0，规定向-X方向走一步若Fi<0，规定向+Y方向走一步2）顺圆插补若Fi≥0，规定向-Y方向走一步若Fi<0，规定向+y方向走一步（3）终点判别1）判断插补或进给的总步数：2）分别判断各坐标轴的进给步数：（4）例对于第一象限圆弧AB，起点A（4，0），终点B（0，4）。