教案《竖直平面内的圆周运动实例分析》

竖直平面内的圆周运动及实例分析竖直平面内的圆周运动一般是变速圆周运动(带电粒子在匀强磁场中运动除外)，运动的速度大小和方向在不断发生变化，运动过程复杂，合外力不仅要改变运动方向，还要改变速度大小，所以一般不研究任意位置的情况，只研究特殊的临界位置──最高点和最低点。

一、两类模型——轻绳类和轻杆类1．轻绳类。

运动质点在一轻绳的作用下绕中心点作变速圆周运动。

由于绳子只能提供拉力而不能提供支持力，质点在最高点所受的合力不能为零，合力的最小值是物体的重力。

所以：（1）质点过最高点的临界条件：质点达最高点时绳子的拉力刚好为零，质点在最高点的向心力全部由质点的重力来提供，这时有，式中的是小球通过最高点的最小速度，叫临界速度；（2）质点能通过最高点的条件是；（3）当质点的速度小于这一值时，质点运动不到最高点高作抛体运动了；（4）在只有重力做功的情况下，质点在最低点的速度不得小于，质点才能运动过最高点；（5）过最高点的最小向心加速度。

2．轻杆类。

运动质点在一轻杆的作用下，绕中心点作变速圆周运动，由于轻杆能对质点提供支持力和拉力，所以质点过最高点时受的合力可以为零，质点在最高点可以处于平衡状态。

所以质点过最高点的最小速度为零，（1）当时，轻杆对质点有竖直向上的支持力，其大小等于质点的重力，即；（2）当时，；（3）当，质点的重力不足以提供向心力，杆对质点有指向圆心的拉力；且拉力随速度的增大而增大；（4）当时，质点的重力大于其所需的向心力，轻杆对质点的竖直向上的支持力，支持力随的增大而减小，；（5）质点在只有重力做功的情况下，最低点的速度，才能运动到最高点。

过最高点的最小向心加速度。

过最低点时，轻杆和轻绳都只能提供拉力，向心力的表达式相同，即，向心加速度的表达式也相同，即。

质点能在竖直平面内做圆周运动（轻绳或轻杆）最高点的向心力最低点的向心力，由机械能守恒，质点运动到最低点和最高点的向心力之差，向心加速度大小之差也等于。

《竖直平面内的圆周运动》教学设计一、教材分析本节教学内容——《竖直平面内的圆周运动》，是高中物理2019版新教材必修2第六章第4节《生活中的圆周运动》之后应该专题复习的内容，这部分是历年高考的热点和难点，作为高三的复习课更需要结合动能定理，能量守恒等关系来进行复习。

二、学情分析在进行教学之前学生已掌握：物体做圆周运动的条件n F F =合，向心力表达式r T m r m r v F 2222n 4m πω===，对物体的受力分析等基本知识。

基础较好的学生也能知道物体在竖直面内要做圆周运动的条件，但是绝大多数学生还是停留在“印象”当中，要不就是“记得”要满足gR v ≥这个条件，对于哪种模型，在哪个位置满足这个条件就说不清。

另外，功能关系的考察是历年来高考的热点、难点内容，在“考纲”当中属于Ⅱ级要求，要求学生能够理解并运用，因此本节复习课会把“绳”模型中小球过最高点的临界条件与功能关系结合进行复习。

三、核心素养（一）物理观念1. 理解“绳”模型中物体做完整圆周运动的条件：物体要过最高点，且最高点速度满足gR v ≥。

2.功能关系的运用（二）科学思维通过实验现象的观察和理论的推导，得出小球要做圆周运动的条件，并结合功能关系进行运用。

（三）科学态度与责任实行新课标之后，高考更加注重对“理解能力”、“分析综合能力”、“实验能力”的考察，我们的备考更多的是做题，甚至是背题、背结论，致使学生无法触类旁通。

根本在于对物理过程分析的缺失，所以高三复习也有必要带着学生从具体的物理现象入手，理解得出的结论，引导学生形成科学探究意识和探究方法，并能够运用从而形成良好的思维习惯。

四、教学重难点重点：“绳”模型中物体完成完整圆周运动的临界条件难点：功能关系的运用五、教学设计（一）轻松一刻1.视频播放汽车过山车2.水流星3.自制大圆环演示4.现象归纳教师说明：刚才的3个情况都属于物体运动到高处时下方没有支撑的情况，我们统称为“绳”模型。

引入竖直面内的圆周运动是典型的变速曲线运动。

涉及知识面比较广，既有临界问题，又有能量守恒的问题，分析时要注意运动模型的区别和临界条件的不同。

我们先来复习一下竖直面内圆周运动的两个典型模型：轻绳、轻杆模型【教师提问】两种模型中物体在最高点受力情况有何不同？【学生回答】．“轻绳”模型和“轻杆”模型不同的原因在于“轻绳”只能对小球产生拉力，而“轻杆”既可对小球产生拉力也可对小球产生支持力。

比较两种模型物理情景最高点无支撑最高点有支撑实例球与绳连接、水流星、沿内轨道的“过山车”等球与杆连接、球在光滑管道中运动等图示异同点受力特征除重力外，物体受到的弹力方向：向下或等于零除重力外，物体受到的弹力方向：向下、等于零或向上受力示意图分组讨论两种模型在最高点物体受力和速度的关系：[基础反馈 ]1、2两题[典例1】半径为R的光滑圆环轨道竖直放置,一质量为m的小球恰能在此圆轨道内做圆周运动,则小球在轨道最低点处对轨道的压力大小为 ( )A.3mgB.4mgC.5mgD.6mg 学生思考并回答问题学生回答两种模型的临界条件讨论并回答问题思考回答问题讨论回答问题【解题探究】(1)如何求小球在轨道最低点的速度?(2)求小球在最低点对轨道的压力,要以谁为研究对象?此题为轻绳模型，重点讲解最高点和最低点的受力情况，和最高点与最低点建立联系的方法-----能量守恒，让学生会运用牛顿第二定律和能量观点解决圆周运动问题。

【典例2】[2015·潍坊模拟]长L＝0.5 m质量可忽略的细杆，其一端可绕O点在竖直平面内无摩擦地转动，另一端固定着一个小球A。

A的质量为m＝2 kg，如图所示，求在下列两种情况下，球在最高点时杆对小球的作用力：(1)A在最低点的速率为21 m/s；(2)A在最低点的速率为6 m/s。

此题要注意杆的弹力是拉力还是支持力，及其方向。

[典例3] [2014·课标全国卷Ⅱ]如图，一质量为M的光滑大圆环，用一细轻杆固定在竖直平面内；套在大环上质量为m的小环(可视为质点)，从大环的最高处由静止滑下。

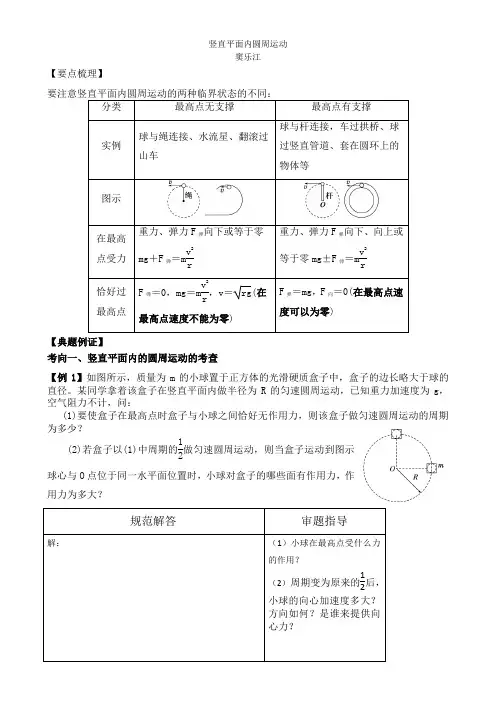
竖直平面内圆周运动窦乐江【要点梳理】要注意竖直平面内圆周运动的两种临界状态的不同：分类 最高点无支撑最高点有支撑实例球与绳连接、水流星、翻滚过山车球与杆连接，车过拱桥、球过竖直管道、套在圆环上的物体等图示在最高点受力 重力、弹力F 弹向下或等于零mg ＋F 弹＝m v 2r重力、弹力F 弹向下、向上或等于零mg±F 弹＝m v 2r恰好过 最高点F 弹＝0，mg ＝m v 2r，v ＝rg(在最高点速度不能为零)F 弹＝mg ，F 向＝0(在最高点速度可以为零)【典题例证】考向一、竖直平面内的圆周运动的考查【例1】如图所示，质量为m 的小球置于正方体的光滑硬质盒子中，盒子的边长略大于球的直径。

某同学拿着该盒子在竖直平面内做半径为R 的匀速圆周运动，已知重力加速度为g ，空气阻力不计，问：(1)要使盒子在最高点时盒子与小球之间恰好无作用力，则该盒子做匀速圆周运动的周期为多少？(2)若盒子以(1)中周期的12做匀速圆周运动，则当盒子运动到图示球心与O 点位于同一水平面位置时，小球对盒子的哪些面有作用力，作用力为多大？规范解答审题指导解：（1）小球在最高点受什么力的作用？（2）周期变为原来的12后，小球的向心加速度多大？方向如何？是谁来提供向心力？【教你一招】：【对应训练】如图甲所示，在同一竖直平面内两正对着的半径为R 的相同半圆光滑轨迹，相隔一定的距离x ，虚线沿竖直方向，一质量为m 的小球能在其间运动。

今在最低点B 与最高点A 各放一个压力传感器，测试小球对轨道的压力，并通过计算机显示出来。

(不计空气阻力，g 取10 m/s 2)(1)要使小球不脱离轨道，求小球在A 点的速度大小；(2)求A 、B 两点的压力差ΔF N 与x 的函数关系；(用m 、R 、g 表示)(3)若测得两点压力差ΔFN 与距离x 的图象如图乙所示。

根据图象，求小球的质量。

考向二、平抛运动与圆周运动的综合考查【例2】(2014·福建·21)(19分)如图所示为某游乐场内水上滑梯轨道示意图，整个轨道在同一竖直平面内，表面粗糙的AB 段轨道与四分之一光滑圆弧轨道BC 在B 点水平相切.点A 距水面的高度为H ，圆弧轨道BC 的半径为R ，圆心O 恰在水面.一质量为m 的游客(视为质点)可从轨道AB 的任意位置滑下，不计空气阻力.(1)若游客从A 点由静止开始滑下，到B 点时沿切线方向滑离轨道落在水面D 点，OD ＝2R ，求游客滑到B 点时的速度v B 大小及运动过程轨道摩擦力对其所做的功W f ；(2)某游客从AB 段某处滑下，恰好停在B 点，又因受到微小扰动，继续沿圆弧轨道滑到P 点后滑离轨道，求P 点离水面的高度h.(提示：在圆周运动过程中任一点，质点所受的向心力与其速率的关系为F 向＝rv m 2)规范解答 审题指导解：（1）游客经历了哪几个阶段，各阶段的受力和运动特点是什么？选择合适的依据解题。

课题：竖直平面内的圆周运动实例分析授课班级：高一14班授课时间：2016年4月12日授课教师：罗华权三维目标：一、知识与技能1、了解竖直平面内的圆周运动的特点；2、会分析汽车过凸形桥最高点和凹形桥最低点的受力情况；3、会分析轻杆、轻绳、管道内的小球做圆周运动在最高点、最低点的受力情况；4、掌握轻杆、轻绳、管道内的小球做圆周运动的临界条件。

二、过程与方法1、通过对圆周运动的实例分析，渗透理论联系实际的观点，提高学生的分析和解决问题的能力。

2、通过对匀速圆周运动的规律也可以在变速圆周运动中使用，渗透特殊性和一般性之间的辨证关系，提高学生的分析能力。

3、运用启发式问题探索教学方法，激发学生的求知欲和探索动机；锻炼学生观察、分析、抽象、建模的解决实际问题的方法和能力。

三、情感态度与价值观1、通过对几个实例的分析，使学生养成仔细观察、善于发现、勤于思考的良好习惯，明确具体问题必须具体分析；2、激发学生学习兴趣，培养学生关心周围事物的习惯；3、养成良好的思维表述习惯和科学的价值观。

教学重点：1、分析汽车过凸形桥最高点和凹形桥最低点的受力情况；2、分析轻绳、圆环内侧轨道、轻杆的小球做圆周运动在最高点、最低点的受力情况。

教学难点：轻绳、圆环内侧轨道、轻杆等模型中的小球在竖直平面内做圆周运动的临界条件及应用。

教学方法：讲授、分析、推理、归纳教学用具：过山车模型、水流星、多媒体课件等课时安排：1课时教学过程：上节课我们对生活中常见的匀速圆周运动进行了实例分析。

知道分析和研究匀速圆周运动的问题，关键是把向心力的来源弄清楚，然后再结合牛顿第二定律解决相关具体问题。

这节课我们将进一步学习竖直平面内的变速圆周运动，生活中有哪些常见的竖直平面内的圆周运动呢？一、汽车过凹凸桥1. 汽车过凸形桥的最高点公路上的拱形桥是常见的，汽车过桥时的运动也可看做圆周运动。

通过提问，引导学生进入状态。

问题1：如果汽车在水平路面上匀速行驶或静止时，在竖直方向上受力如何？问题2：如果汽车在拱形桥顶点静止时，桥面受到的压力如何？问题3：如果汽车在拱形桥上，以某一速度v 通过圆弧半径为R 的拱形桥的最高点的时候，桥面受到的压力如何？引导学生分析受力情况，并逐步求得桥面所受压力。