水力学-第六章管道

7.14虹吸管将A 池中的水输入B 池，已知长度1l =3m ，2l =5m ，直径d =75mm ，两池水面高差H =2m ，最大超高h =1.8m ，沿程摩阻系数λ=0.02，局部损失系数：进口a ζ=0.5，转弯b ζ=0.2，出口c ζ=1，试求流量及管道最大超高断面的真空度。

解： 以下游水面为基准面，从上池水面到下池水面列伯努利方程：22222350.7 1.00.0222220.0752v l v v v v H g d g g g gζλζζ+⎛⎫=+++=++⨯ ⎪⎝⎭b c 进∴ 3.20v ==（m/s ）23.200.07514.144Q vA π==⨯⨯=（L/s ）从C 过流断面到下池水面列伯努利方程：2222222C C C C Cp v l v v z g g d g gαλζρ++=+ 取1C α= ∵C v v =∴251.8 2.010.02 1.00.0752a C C V p p p vH g g g ρρ-⎛⎫==-=++-⨯- ⎪⎝⎭25 3.203.80.02 3.100.07529.807=-⨯⨯=⨯m答：流量14.14Q =L/s ，管道最大超高断面的真空度为3.10m 。

7.16水从密闭容器A ，沿直径d =25mm ，长l =10m 的管道流入容器B ，已知容器A 水面的相对压强1p =2at ，水面高1H =1m ，2H =5m ，沿程摩阻系数λ=0.025，局部损失系数：阀门v ζ=4.0，弯头b ζ=0.3，试求流量。

解： 以地面为基准面，从A 池面到B 池面列伯努利方程：222111222123222v b p v p v l v H H g g g g d g ααζζζζλρρ⎛⎫++=+++++++ ⎪⎝⎭进出取120v v ==；20p =；0.5ζ=进； 1.0ζ=出，则有121122100.5 1.0 4.030.30.0250.025p g H H g v ρ⎡⎤⎛⎫+-⎢⎥⎪⎝⎭⎢⎥=⎢⎥⎛⎫+++⨯+⨯ ⎪⎢⎥⎝⎭⎣⎦ ()122120516.4g ⨯+-⎡⎤=⎢⎥⎣⎦4.37=（m/s ）24.370.025 2.154Q vA π==⨯⨯=（l /s ）答：流量 2.15Q =l /7.17水车由一直径d =150mm ，长l =80m 的管道供水，该管道中有两个闸阀和4个90°弯头（λ=0.03，闸阀全开a ζ=0.12，弯头b ζ=0.48）。

第六章恒定管流1、并联管道中各支管的单位机械能损失相同，因而各支管水流的总机械能也应相等。

( )2、图示虹吸管中B点的压强小于大气压强。

( )3、恒定管流的总水头线沿流程下降，而测压管水头线沿流程可升可降。

( )4、在等直径圆管中一定发生均匀有压流动。

( )5、各并联支管的水头损失相同，所以其水力坡度也相同。

( )6、图示两个容器由两根直管相连，两管的管径、管长及糙率均相同，所以通过的流量相等。

( )径偏小，不能通过要求的设计流量。

( )8、图示A、B 两点间有两根并联管道 1 和 2 。

设管 1 的沿程水头损失为h f1,管 2 的沿程水头损失为h f2。

则h f1与h f2 的关系为（）（1）h f1 ＞h f2；（2）h f1＜h f2；（3）h f1 = h f2；（4）无法确定。

9、图示为坝身下部的三根泄水管 a、b、c，其管径、管长、上下游水位差均相同，则流量最小的是（）。

（1）a管；（2）b管；（3）c管；（4）无法确定。

10、在管道断面突然扩大处，测压管水头线沿程________________________________________________________；在管道断面突然缩小处，测压管水头线沿程____________________________________。

11、图示为一串联管段恒定流。

各管段流量q v1、q v2、q v3的关系为______________________。

各管段流速 v1、v2、v3 的关系为________________________________________________________ ____。

12、对于有压管流出口为自由出流时，测压管水头线终点在_________________________________________________；出口为淹没出流时，若下游水池中流速v2=0,测压管水头线终点在____________________________，若v2≠0，测压管水头线应________________________________________________________ ____________下游水面。

选择题（单选题）1.水在垂直管内由上向下流动，测压管水头差h，两断面间沿程水头损失，则：（a）（a）hf=h；（b）h f=h+l；（c）h f=l－h；（d）h f=l。

2.圆管流动过流断面上切应力分布为：（b）（a）在过流断面上是常数；（b）管轴处是零，且与半径成正比；（c）管壁处是零，向管轴线性增大；（d）按抛物线分布。

3.圆管流的雷诺数（下临界雷诺数）：（d）（a）随管径变化；（b）随流体的密度变化；（c）随流体的黏度变化；（d）不随以上各量变化。

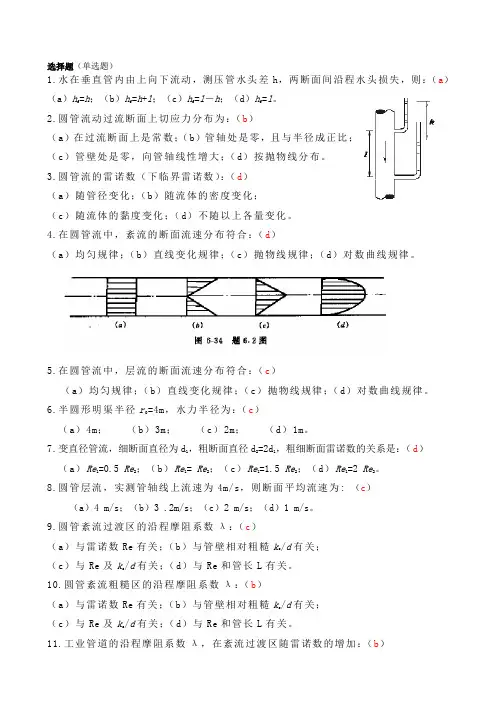
4.在圆管流中，紊流的断面流速分布符合：（d）（a）均匀规律；（b）直线变化规律；（c）抛物线规律；（d）对数曲线规律。

5.在圆管流中，层流的断面流速分布符合：（c）（a）均匀规律；（b）直线变化规律；（c）抛物线规律；（d）对数曲线规律。

6.半圆形明渠半径r0=4m，水力半径为：（c）（a）4m；（b）3m；（c）2m；（d）1m。

7.变直径管流，细断面直径为d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是：（d）（a）Re1=0.5 Re2；（b）Re1= Re2；（c）Re1=1.5 Re2；（d）Re1=2 Re2。

8.圆管层流，实测管轴线上流速为4m/s，则断面平均流速为: （c）（a）4 m/s；（b）3 .2m/s；（c）2 m/s；（d）1 m/s。

9.圆管紊流过渡区的沿程摩阻系数λ：（c）（a）与雷诺数Re有关；（b）与管壁相对粗糙k s/d有关；（c）与Re及k s/d有关；（d）与Re和管长L有关。

10.圆管紊流粗糙区的沿程摩阻系数λ：（b）（a）与雷诺数Re有关；（b）与管壁相对粗糙k s/d有关；（c）与Re及k s/d有关；（d）与Re和管长L有关。

11.工业管道的沿程摩阻系数λ，在紊流过渡区随雷诺数的增加：（b）（a ）增加；（b ）减小；（c ）不变；（d ）不定。

计算题【6.12】水管直径d =10cm ，管中流速v =1m/s ，水温为10℃，试判别流态。

第六章 流动阻力与能量损失本章首先讨论实际流体在运动过程中的能量损失的分类和计算公式，公式中损失系数的确定将是这一章主要的内容。

由于粘性的影响，实际流体的流动会呈现出两种不同的型态 — 层流和紊流，它们的流场结构和动力特性区别很大，必须加以判别，并分别研究。

由均匀流流动的特点，导出了均匀流的沿程损失与切应力之间的关系，圆管层流类似于均匀流，因此得到了圆管层流的沿程损失的计算方法。

由于在紊流流场中存在随机的脉动量，须对瞬时量取统计平均，分别讨论平均流动和脉动量。

紊流中切应力包含了粘性切应力和附加切应力（雷诺应力），采用混合长度理论建立起附加切应力与时均流速之间的关系。

本章还紊流运动中的局部水头损失的计算方法。

§6—1 流动阻力和能量损失的两种形式● 实际流体在渐变流段中流动，由流管壁面上粘性切应力形成的阻力称为沿程阻力或摩擦阻力。

在均匀流段上这种阻力是沿程不变的。

为克服沿程阻力形成的能量损失，称为沿程损失，沿程损失随着流程的增加而增加。

在均匀流段上每单位流程上的沿程损失是常数，沿程损失与流程长度呈正比例关系。

单位重量流体的沿程损失用 hf 表示，称为沿程水头损失。

计算公式为：gv d l h f 22λ= ● 在流管边壁沿程急剧变化，流速分布急剧调整的局部区段上，集中产生的流动阻力称为局部阻力。

由局部阻力引起的水头损失，称为局部水头损失，以 hj 表示，如管道进口、异径管、弯管、三通、阀门等各种管件处的水头损失，都是局部水头损失。

计算公式为：gv h j 22ζ= ● 若断面1至断面2的一段管路由若干段渐变流段组成，其间又有若干处局部损失，则这段管路的能量损失为所有沿程损失和局部损失的总和。

§6—2 流动的两种型态● 实际流体的流动会呈现出两种不同的型态：层流和紊流，它们的区别在于：流动过程中流体层之间是否发生混掺现象。

在紊流流动中存在随机的脉动量，而在层流流动中则没有。

● 1883年，雷诺试验表明：圆管中恒定流动的流态转化取决于雷诺数νvdR e =，d 是圆管直径，v 是断面平均流速，ν是流体的运动粘性系数。

第六章明渠恒定均匀流人工渠道、天然河道以及未充满水流的管道等统称为明渠。

明渠流(Open Channel Flow)是一种具有自由表面的流动，自由表面上各点受当地大气压的作用，其相对压强为零，所以又称为无压流动。

与有压管流不同，重力是明渠流的主要动力，而压力是有压管流的主要动力。

明渠水流根据其水力要素是否随时间变化分为恒定流和非恒定流动。

明渠恒定流动又根据流线是否为平行直线分为均匀流和非均匀流。

明渠流动与有压管流的一个很大区别是：明渠流的自由表面会随着不同的水流条件和渠身条件而变动，形成各种流动状态和水面形态，在实际问题中，很难形成明渠均匀流。

但是，在实际应用中，如在铁路、公路、给排水和水利工程的沟渠中，其排水或输水能力的计算，常按明渠均匀流处理。

此外，明渠均匀流理论对于进一步研究明渠非均匀流也具有重要意义。

§6-1 概述1．明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响，因此在水力学中把明渠分为以下类型。

(1)棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道，称为棱柱形渠道，否则为非棱柱形渠道。

前者的过水断面面积A仅随水深h变化，即A=f(h)；后者的过水断面面积不仅随水深变化，而且还随着各断面的沿程位置而变化，即A=f(h,s)，s为过水断面距其起始断面的距离。

(2)顺坡(正坡)、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差，称为明渠的底坡(Bottom slope)，用i表示，如图6-1a，1-1和2-2两断面间，渠底线长度为Δs，该两断面间渠底高程差为(a1-a2)=Δa，渠底线与水平线的夹角为θ，则底坡i为。

图6-1θsin 21=∆∆=∆-=sas a a i (6-1-1) 在水力学中，规定渠底高程顺水流下降的底坡为正，因此，以导数形式表示时应为dsdai -= (6-1-2) 当渠底坡较小时，例如i ＜0.1或θ＜6°时，因两断面间渠底线长度Δs ，与两断面间的水平距离Δl ，近似相等，Δs ≈Δl ，则由图6-1a 可知θtan =∆∆≈∆∆=la s a ii=sin θ≈tg θ (6-1-3) 所以，在上述情况下，两断面间的距离Δs 可用水平距离Δl 代替，并且，过水断面可以看作铅垂平面，水深h 也可沿铅垂线方向量取。