第六章 外部绕流
- 格式:ppt
- 大小:14.43 MB
- 文档页数:59




第六章流体力学基础知识流体力学是研究流体平衡和宏观运动规律,以及流体与所接触物体之间相互作用的力学特点,用以分析解决工程设计和使用中的实用问题。
液体和气体统称为流体。
流体的特征是具有流动性,即其抗剪和抗张的能力很小;无固定形状,随容器的形状而变化;在外力作用下其内部发生相对运动。
石油工业中处理的物料多数是流体。
运用流体力学的一般原理,研究设备中流体运动的规律及其对生产过程的影响,为石油工业诸学科提供理论基础,这就是流体力学的主要内容。
例如,了解、研究流体速度、压力、密度等在设备内的分布和随时间的变化以及处于流体中的物体,如推动流体运动的部件(搅拌桨叶等),悬浮颗粒(或液滴、气泡)与流体之间的相互作用等。
研究流体运动的规律,首先需要了解影响流体运动的基本因素。
这既包括流体本身的属性,也包括能容纳并使其流动的设备(如管道、塔器、容器、换热器、泵、鼓风机、压缩机等)的特性。
因此,不同的流动问题受不同的复杂因素的支配。
本章仅对石油工业中常遇到的流体力学问题加以概括地说明。
第一节流体运动概述在石油工业生产中所处理的原料及产品,大多数是流体。
按照生产工艺的要求,制造产品时往往把它们依次输送到各设备内,进行化学反应或物理变化,制成的产品又常需要输送到储罐内储存。
过程进行的好坏,动力的消耗及设备的投资都与流体的流动状态密切相关。
一、流体的物理属性流体的物理性质是流体运动状态变化的内因。
对于流体运动有影响的物性,主要有密度、粘性、压缩性、表面张力等。
为了论述流体的上述宏观特性,这里先阐明流体力学中的一个基本假定——流体是连续介质。
1、连续介质假定流体是由运动的分子组成的,分子之间有着相当大的空隙,大量分子作随机运动,因而导致流体的质量在空间和时间上的分布是不连续的,而且具有随机性。
但在流体力学中研究流体的运动规律时,考察的是由大量分子所组成的流体质点的宏观运动规律,不着眼于个别分子的微观运动状况;注重的是整个设备(流场)范围内的变化,而不是分子平均自由程那样微小距离上的差异。






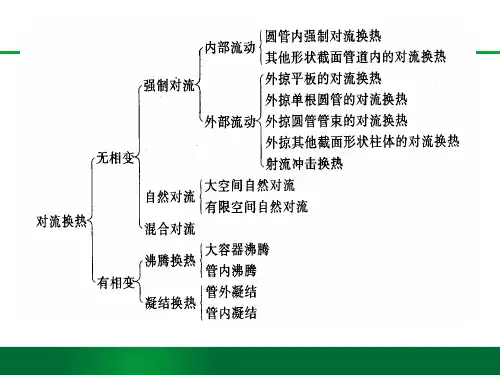
第六章 单相流体对流换热及准则关联式第一节 管内受迫对流换热本章重点:准确掌握准则方程式的适用条件和定性温度、定型尺寸的确定。
1-1 一般分析),,,,,,,,(l c t t u f h p f w μαρλ=流体受迫在管内对流换热时,还应考虑以下因素的影响:① 进口段与充分发展段,② 平均流速与平均温度,③ 物性场的不均匀性,④ 管子的几何特征。
一、进口段与充分发展段1.流体在管内流动的主要特征是,流动存在着两个明显的流动区段,即流动进口(或发展)段和流动充分发展段,如图所示。
(1)从管子进口到边界层汇合处的这段管长内的流动称为管内流动进口段。
(2)进入定型流动的区域称为流动充分发展段。
在流动充分发展段,流体的径向速度分量v 为零,且轴向速度u 不再沿轴向变化,即:0=∂∂xu, 0=v 2.管内的流态(1)如果边界层在管中心处汇合时流体流动仍然保持层流,那么进入充分发展区后也就继续保持层流流动状态,从而构成流体管内层流流动过程。
2300Re <用νdu m =Re 判断流态, 式中 m u 为管内流体的截面平均流速, d 为管子的内直径,ν 为流体的运动黏度。
(2)如果边界层在管中心处汇合时流体已经从层流流动完全转变为紊流流动,那么进入充分发展区后就会维持紊流流动状态,从而构成流体管内紊流流动过程。
410Re >(3)如果边界层汇合时正处于流动从层流向紊流过渡的区域,那么其后的流动就会是过渡性的不稳定的流动,称为流体管内过渡流动过程。
410Re 2300<<3.热进口段和热充分发展段当流体温度和管壁温度不同时,在管子的进口区域同时也有热边界层在发展,随着流体向管内深入,热边界层最后也会在管中心汇合,从而进入热充分发展的流动换热区域,在热边界层汇合之前也就必然存在热进口区段。
随着流动从层流变为紊流, 热边界层亦有层流和紊流热边界层之分。
热充分发展段的特征对常物性流体,在常热流和常壁温边界条件下,热充分发展段的特征是:)(1x f t f =及)(2x f t w =与管内任意点的温度),(r x f t =组成的无量纲温度⎪⎪⎭⎫⎝⎛--x f x w w t t t t ,,x ,随管长保持不变,即:0,,x ,=⎪⎪⎭⎫ ⎝⎛--∂∂x f x w w t t t t x 式中,t —管内任意点的温度,),(r x f t = ⇒xf x w w t t tt ,,x ,--仅是r 的函数。
第六章 实际流体的绕流运动Chapter Six Cross-flow Movement of Real Fluid一、研究内容1.实际流体绕流物型时所产生的问题,如速度和压强分布;边界层分离现象;绕流阻力与升力等等。
2.实际流体绕流物型时,不能忽略流体黏性的影响,并且流体与物体间存在相互作用力。
工程中绕流问题很常见,如锅炉中烟气横向流过受热面管束;汽轮机、轴流式泵或风机等设备中流体绕流叶栅;飞机在空中飞行、船只在海中航行等等。
二、研究方法以N-S 方程及速度边界层理论为基础研究实际流体的绕流问题。
第一节 纳维-斯托克斯方程(N-S 方程)Section One The Navier-Stokes Equation(N-S Equation)一、不可压缩流体的N-S 方程的形式其中,方程等号左侧为全加速度,可以展开为因此,不可压缩流体的N-S 方程三个方程式,每个方程含有9项内容,方程较复杂。
二、不可压缩流体N-S 方程的说明1.方程等号左侧为全加速度,即是惯性力项;等号右侧第一项是质量力项,第二项为压力项,第三项为黏性力项。
其实质可以理解为实际流体的牛顿第二定律(也即是机械能转换与守恒定律的应用)。
2.若运动黏度0=ν,则N-S 方程转变为欧拉运动微分方程;若运动黏度0=ν,且全加速度0/=dx du 、0/=dy dv 及0/=dz dw ,则N-S 方程转变为欧拉平衡微分方程。
3. N-S 方程结合不可压缩流体的连续性方程0=∂∂+∂∂+∂∂z w y v x u ,若其余量已知,理论上可求得速度一压强分布u 、v 、w 及p 。
但N-S 方程在数学上求解相当困难,通常采用近似解。
第二节 边界层理论Section Two Velocity Boundary Layer Theory一、理论的提出针对工程中出现的大雷诺数Re 下实际流体绕流物型时所产生的若干问题,如速度和压强分布;边界层分离现象;绕流阻力与升力等,并成功解决了达朗贝尔(D ’Alembert)疑题,即势流理论所得到的绕流物型时可能只有升力而无阻力的结论与实际情况截然相反的现象。