第三章直方图
- 格式:doc
- 大小:101.00 KB
- 文档页数:6


3。
5。
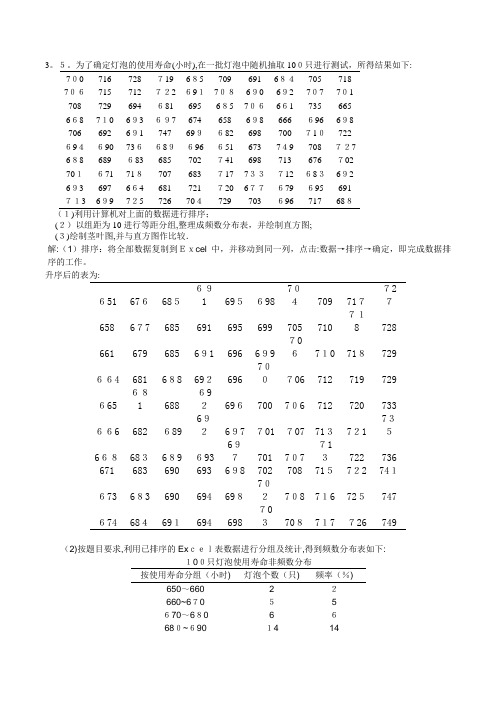
为了确定灯泡的使用寿命(小时),在一批灯泡中随机抽取100只进行测试,所得结果如下: 700 716 728 719 685 709 691 684705 718706715 712 722 691708690 692 707 701708 729 694 681 695 685 706661 735 665668 710 693 697 674 658 698 666 696 698706 692 691 747 699682 698 700 710722694690 736689696 651 673 749 708 727688 689 683 685 702 741 698 713 676 702701671 718707 683 717 733712 683692693 697 664 681 721 720 677679 695 691713 699 725 726 704729 703 696 717 688(1)利用计算机对上面的数据进行排序;(2)以组距为10进行等距分组,整理成频数分布表,并绘制直方图;(3)绘制茎叶图,并与直方图作比较.解:(1)排序:将全部数据复制到Excel中,并移动到同一列,点击:数据→排序→确定,即完成数据排序的工作。
升序后的表为:651 676685691 695698704709 717727658 677 685 691 695 699 705 710 718 728661 679 685 691 696 699 706710 718729664 681 688 692696 700706 712 719 729665 681 688692696700 706 712 720 733666 682 689 692697 701 707 713721735668683689 693 697701 707713722 736671 683 690 693 698 702 708 715722 741673 683 690 694 698702708 716 725747674 684691694 698 703708717 726 749(2)按题目要求,利用已排序的Excel表数据进行分组及统计,得到频数分布表如下:100只灯泡使用寿命非频数分布按使用寿命分组(小时) 灯泡个数(只) 频率(%)650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 2626700~7101818710~720 1313720~7301010730~740 3 3740~750 3 3合计100100(3)制作直方图:将上表(包含总标题,去掉合计栏)复制到Excel表中,选择全表后,点击:图表向导→柱形图→选择子图表类型→完成。



13
第三章 直方图
直方图是用一系列等宽不等高的长方形来表示,宽度表示数据范围的间隔,
高度表示在给定间隔内数据出现的频数,变化的高度形态表示数据的分布情况。
直方图一般用于显示波动的形态,直观地传达有关过程情况的信息和决定
在何处集中力量进行质量改进。根据直方图提供的信息,可以推算出数据分布
的各种特性值和工序能力指数和工序的不合格品率。
一、收集数据:收集所需的数据,并将其填入数据表。一般经常采取的数
据个数为50~200个,组数常在6~15范围内。否则反映分布及随后的各种推算
会有很大的误差。
二、确定组距和组数:组距选取时最好为测量单位1、2、5的倍数。
求出步骤:
a计算极差R。从数据中选出最大值和最小值,这时应去掉相差悬殊的异
常数据。用最大值减最小值所得结果即为极差。
b用测量单位的1、2、5的倍数除极差,并将所得值修整。
c将圆整值对照下表确定组数,这时圆整值对应的测量单位的倍数值即为
组距。 组数表
数据数 50以内 50~100 100~250 250以上
组数
5~7 6~10 7~15 10~30
d确定分组组界:把数据中的最小值分在第一组的中部,并把分组组界定
在最小测量单位的1/2处,以避免测量值恰好落在边界上。第一组下限值为最
小值-最小测量单位/2,第一组的上限为下限值加上组距。依次类推,直至它包
括最大值的末一组的上界为止。
三、作频数分布表
14
a填入顺序号及各组界限值。
b计算各组的组中值:X中=
上界限值+下界限值
c统计各组频数
四、作直方图 :
用横坐标标注质量特性的测量值的分界值,纵坐标标注频数值,各组的频
数用直方柱的高度表示,就形成了直方图。
确定横坐标刻度时要考虑包括数据的整个分布范围,确定纵坐标刻度时,
应考虑最大刻度值要包容最大频数的组。在图内作必要的说明(如图名、收集
数据的时间和地点、总频数、统计特性值等)。
五、图形分析
常用的分析方法有图形分析和对照标准(规格)分析。
图形分析对质量特性计量值而言,其数据分布大体上符合正态分布。在正
常的生产情况下,其直方图的形状也应呈现出正常的形态;当有异常因素影响
时,直方图的图形也呈现出异常。
正常型(对称型)正常型的直方图形,中间高、两边低,左右基本对称。
这说明工序处于稳定的正常状态。
孤岛型:在远离主分布的地方出现小的直方形,犹如孤岛,孤岛型直方图
说明在生产过程中短时间内有异常因素在起作用,使加工条件发生变化。
偏向型:直方图的顶峰偏向一侧,形成不对称的形状。偏向型直方图的出
现,往往是由于工人操作的偏差造成的,如加工孔往往偏向负公差,而加工轴
往往偏向正公差。
双峰型:直方图的图形出现两个高峰。双峰型直方图的数据来自两个总体,
如两批材料制成的产品、两种设备加工的产品或两种工艺方法制造的产品混合
15
所取得的数据。
平顶型:直方图呈现平顶形,完全不符合正态分布的规律。平顶型直方图,
往往是由于生产过程中缓慢变化的因素在起主导作用。
锯齿型:直方图内的各直方大量出现高度上的参差不齐,但整个图形总体
看来还保持中间高、两边低、左右基本对称的形状。锯齿型直方图一般说来,
生产过程中没有显著的异常因素起主导作用,是由于作直方图时,分组过多或
测量时仪有误差过大造成。
a正常型 b孤岛型 c偏向型
d双峰型 e平顶型 f锯齿型
对照标准分析对照标准分析是指将直方图放到标准(规格)界限之中去分
析的一种方法,主要用于判断工序满足标准(规格)的程度,用以分析工序能
力。
以下所分析的各种图形中,“T”表示标准范围(公差),“B”表示实际分
布的范围(即6σ)
理想型:理想型直方图的分布中心(X)与公差中心相重合,B被包在T
的中间,实际分布的两边与规格界限有一定余量。此时T=8σ,所以工序能力
指数为Cp=1.33。
16
TL TU TL T=B TU TL T TU
a 理想型 b无富余型 c能力富余型
TL T TU TL T TU T
L T TU
B
B
d能力不足型 e偏心型 f陡壁型
无富余型:无富余型直方图虽然实际分布也落在规格范围之内,但完全没
有余量。此时,T=B=6σ,所以工序能力指数Cp=1。
能力富余型:能力富余型直方图的图形只占规格范围中间的很小一部分,
说明规格范围过分大于实际分布范围,此时T≥10σ,所以工序能力指数Cp≥
1.67,虽然工序具有良好的加工能力,质量状况很好,但属于不经济的加工。
能力不足型:能力不足型直方图的图形大大超过了规格范围,说明生产过
程中有大量不合格品发生。此时工序的质量波动太大,工序能力不足,T≤4б,
所以工序能力指数Cp≤0.67
偏心型:偏心型直方图的分布范围虽然在规格界限内,但分布中心(X)偏
离规格中心,故有超差的可能。这种情况的出现是由于工艺参数不当所造成,
工序能力指数需用公式Cpk= T—2ε计算,计算式中“ε”为分布中心与规格
中心的偏移量,调整工艺参数,使偏移量ε=0时,工序质量会得到改善。
陡壁型:陡壁型直方图是不完整的直方图。这是由于工序控制不好,实际
分布过分偏离规格中心,造成超差或废品。但在作直方图时,数据中已将不合
17
格品剔除,所以没有超出规格界限外的直方部分。
六应用举例
a收集数据如下表
手柄力矩(N.m)
1.49 1.32 1.44 1.35 1.20 1.19 1.37 1.31 1.25 1.34
1.19 1.11 1.16 1.11 1.44 1.29 1.29 1.42 1.59 1.38
1.28 1.12 1.45 1.36 1.25 1.40 1.35 1.11 1.38 1.33
1.15 1.30 1.12 1.33 1.26 1.35 1.44 1.32 1.11 1.38
1.27 1.37 1.26 1.20 1.35 1.45 1.26 1.37 1.32 1.23
1.28 1.44 1.40 1.31 1.18 1.31 1.25 1.24 1.32 1.22
1.22 1.37 1.19 1.47 1.14 1.37 1.32 1.12 1.38 1.30
1.25 1.40 1.24 1.50 1.19 1.07 1.31 1.23 1.18 1.32
1.38 1.00 1.41 1.40 1.37 1.35 1.12 1.29 1.48 1.20
1.31 1.20 1.35 1.24 1.47 1.12 1.27 1.38 1.40 1.31
1.52 1.42 1.52 1.24 1.25 1.20 1.31 1.15 1.03 1.28
1.29 1.47 1.41 1.32 1.22 1.28 1.27 1.22 1.32 1.54
1.42 1.34 1.15 1.29 1.21
b计算极差R=1.59-1.00=0.59
c确定组数与组距0.59/0.01=59 0.59/0.02=29.5≈30 0.59/0.05=11.8≈12
对照组数表可知选取组数12是合理的,组距相应为0.05。
d确定组界:第一组下界为最小值-最小测量单位/2=1.00-0.01/2=0.995
第一组上界为0.995+0.05=1.045,第一组上界及为第二组下界,以此类推确定
出各组分界值。
e填入频数分布表
18
频数分布表
组号 组距 组中值 频数符号 频数
1 2 3 4 5 6 7 8 9 10 11 12 0.995~1.045 0.045~1.095 1.095~1.145 1.145~1.195 1.195~1.245 1.245~1.295 1.295~1.345 1.345~1.395 1.395~1.445 1.445~1.495 1.495~1.545 1.545~1.595 1.02 1.07 1.12 1.17 1.22 1.27 1.32 1.37 1.42 1.47 1.52 1.57 / / / //// //// //// //// //// //// //// / //// //// //// //// //// //// //// //// / //// //// //// //// //// //// //// //// // //// / 2
1
10
10
16
20
21
19
14
7
4
1
合计
125
f画直方图:纵坐标表示频数,横坐标表示质量特性值。
22 Tu
18
14
10
6
2
0.995 1.045 1.095 1.145 1.195 1.245 1.295 1.345 1.395 1.445 1.495 1.545 1.595 1.8 N.m
g图形分析:从图形可以看出,此直方图的顶峰偏向一侧,为不对称形状,
所以属于偏向形。分析原因可能是工人操作上的原因所造成。
对照标准分析将直方图放到标准界限内
X=ΣX/n=1.30 S=Σ(X-X)2/(n-1)=0.113
CP=(TU-X)/3S=(1.8-1.30)/3×0.113=1.175 可知工序能力尚可,但不很充分。