当前位置：文档之家 › 模糊控制系统课件4.3(ts型系统)

模糊控制系统课件4.3(ts型系统)

  • 格式：ppt
  • 大小：119.50 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

第四章 模糊控制系统

第四章 模糊控制系统

常规反馈控制系统结构
今天， 今天，常规的反馈控制方法在实际过程中已经得到广泛 应用，例如在阿波罗登月舱的姿态控制、宇宙飞船、 应用，例如在阿波罗登月舱的姿态控制、宇宙飞船、导弹制 导以及在工业生产过程控制等。但是， 导以及在工业生产过程控制等。但是，对于常规反馈控制系 统，控制器的设计无论是采用经典控制理论还是现代控制理 都需要事先知道被控制对象精确的数学模型。 论，都需要事先知道被控制对象精确的数学模型。也就是说 系统的分析与综合都是建立在数学模型的基础上。 系统的分析与综合都是建立在数学模型的基础上。 然而，在实际控制中被控对象的精确数学模型很难建立， 然而，在实际控制中被控对象的精确数学模型很难建立， 甚至无法建立。例如，交通系统、经济系统及生物发酵过程 甚至无法建立。例如，交通系统、 这样，基于数学模型的控制方法则陷入了困境。 等。这样，基于数学模型的控制方法则陷入了困境。值得注 意的是对于上述的复杂过程， 意的是对于上述的复杂过程，有经验的专家或操作人员用手 动控制的方式，却可以收到令人满意的效果。 动控制的方式，却可以收到令人满意的效果。面对这样的事 人们考虑能否让计算机模拟人的思维方式， 实，人们考虑能否让计算机模拟人的思维方式，对这些复杂 过程进行控制决策。 过程进行控制决策。
x = (ω ,θ ) ɺ x = f ( x, u )
u1 u= u 2
其中u为一个有约束的控制向量， 为前轮的角度， 其中 为一个有约束的控制向量，u1为前轮的角度， u2为车 为一个有约束的控制向量 速。
如果把邻近两辆车定义为 x（执行中的约束），用集合 （执行中的约束） 表示，而两辆停着的车之间的空隙定义为Г（ 表示，而两辆停着的车之间的空隙定义为 （允许的终端状 态的集合） 那么， 停车问题就转化为寻找一个控制律u(t)， 态的集合 ） 。 那么 ， 停车问题就转化为寻找一个控制律 ， 使其在满足各种约束的条件下把初始状态转移到终端状态Г 使其在满足各种约束的条件下把初始状态转移到终端状态 中去。对于这个问题若采用基于数学模型的精确方法来求解， 中去。对于这个问题若采用基于数学模型的精确方法来求解， 由于约束条件过多，求解过程将异常复杂。 由于约束条件过多，求解过程将异常复杂。 但在实际停车时，汽车司机并不考虑控制律u(t)的求解。 的求解。 但在实际停车时，汽车司机并不考虑控制律 的求解 而是凭借以往的经验，先让车向前运动， 而是凭借以往的经验，先让车向前运动，前轮先向右而后向 然后使车向后运动，前轮仍先向右而后向左， 左，然后使车向后运动，前轮仍先向右而后向左，经过多次 反复，车将横向移动一个所需要的距离， 反复，车将横向移动一个所需要的距离，最后向前开停在空 隙处。这样，汽车司机通过一些不精确的观察，执行一些不 隙处。 这样， 汽车司机通过一些不精确的观察， 精确的控制，却达到了准确停车的目的。 精确的控制，却达到了准确停车的目的。

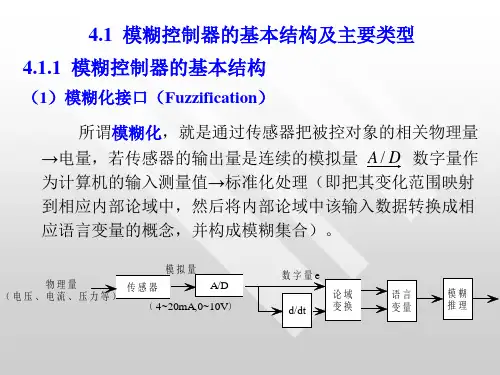
模糊控制系统课件

模糊控制系统课件
4.1 模糊控制器的基本结构及主要类型 4.1.1 模糊控制器的基本结构
（1）模糊化接口（Fuzzification）
所谓模糊化，就是通过传感器把被控对象的相关物理量 →电量，若传感器的输出量是连续的模拟量 A / D 数字量作 为计算机的输入测量值→标准化处理（即把其变化范围映射 到相应内部论域中，然后将内部论域中该输入数据转换成相 应语言变量的概念，并构成模糊集合）。
量化因子：K e
2n1 eH eL
， Kec
2n2 eH eL
，
比例因子：
Ku
uH uL 2m
注：误差和误差变化这两个变量的连续值与其论域中的离散值
并不是一一对应的。
（2）模糊推理机（Inference engine） 模糊推理机由知识库（数据库和规则库）与模糊
推理决策逻辑构成。这是基本部分。 ①知识库（Knowledge base）=数据库（Date base） +语言控制规则库（Rule base）
缺点：不同被控对象，控制规则不变，控制效果不好。
图4.3 简单模糊控制器的结构
⑵模糊自调整控制器----二维模糊控制器中加入修正因子
（规则自调整模糊控制器）
u e 1 e
低阶控制系统： >0.5 高阶控制系统： <0.5
当误差较大时，控制系统的主要任务是消除误差，加快响 应速度，这时对误差的加权应该大些；
的概念？ 3、常用的模糊控制器有哪些？ 4、二维FC的工作原理？优缺点？ 5、FC设计的两种实现方式及其特点？ 6、设计模糊控制器的步骤？
4.2模糊控制器的结构设计
4.2.1模糊控制器的结构设计 实质：模糊控制器输入语言变量及输出语言变量的选取和模糊控制器的不同

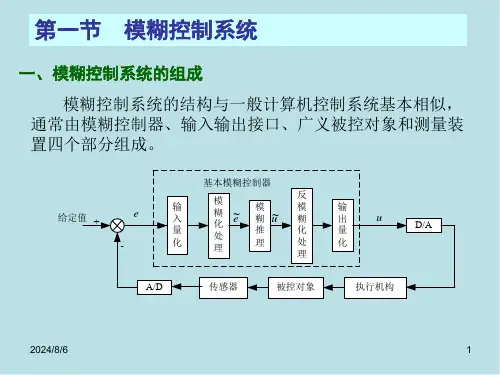
计算机控制系统第5章模糊控制课件

计算机控制系统第5章模糊控制课件

与其隶属
度 A(xi ) 之间的对应关系；“＋”也不表示“求和”，而是表示
模糊集合在论域上的整体。
2024/8/6
5
2．几种典型的隶属函数 （1）高斯型隶属函数
( xc)2
f (x; ,c) e 2 2
2024/8/6
6
（2）S形隶属函数
f
(x;
a,
c)
1
1 ea(xc)
2024/8/6
7
（3）梯形隶属函数
第一节 模糊控制系统
一、模糊控制系统的组成
模糊控制系统的结构与一般计算机控制系统基本相似， 通常由模糊控制器、输入输出接口、广义被控对象和测量装 置四个部分组成。
基本模糊控制器
给定值 +
e
-
输 入 量
化
模
糊 化
e~
处
理
模
糊 u~
推
理
反 模 糊 化 处
理
输 出 量
化
u
D/A
A/D
传感器
被控对象
执行机构
所谓论域就是被考虑客体所有元素的集合。在模糊控制系
统中，把模糊控制器的输入变量偏差 e 及其变化率 ec 的实际范
围称为这些变量的基本论域。基本论域内的量为精确量，需要 对它们进行量化处理。
在实际控制系统中，需要通过所谓量化因子进行量化处理， 实现论域变换。量化因子的定义为：
ke
2n be ae
kec
a,
b)
1 2( 2(b
x b
x
a a
)2 )2
ba
0
xa
a a
x b
a x
2
b

《模糊控制系统》PPT课件

《模糊控制系统》PPT课件

是所期望的。这促使我们研究模糊系统作为万能
函数逼近器并拥有最小系统构成的必要条件，从
而使这些必要条件能用于指导模糊系统开发者设
计更紧凑的模糊控制器和模糊模型
• 必要条件设置了需要的输入模糊集、输出模糊集 和模糊规则，表明了模糊系统需要的输入模糊集
和模糊规则的数目依赖于被逼近函数的极值点的
数目和位置
精选ppt
“Fuzzy Sets”一文，首次提出了模糊集合的概念
• 1974年英国教授Mamdani首次将模糊集合理论应
用于加热器的控制，他将基于规则系统的想法与
模糊参数相结合来构造控制器，模仿人类操作者
的操作经验
• 1985年Takagi和Sugeno提出了另一类具有线性规
则后项的模糊控制器，称之为Takagi-Sugeno
(1988, Japan)
• Postsurgical patients
(1989, USA)
• Auto focus video camera
(1990, Japan)
• Washing machines
(1990, Japan)
• Air conditioners
(1990, Japan)
• Anti-shaking video camera
控制规律
• 各种类型的Mamdani和TS模糊系统在过去几年中
都被证明是万能逼近器，它们能一致逼近定义在
闭定义域D上的任意连续函数到任意高的逼近精
度。这些模糊系统有：加法模糊规则系统、模糊
输入—输出控制器、Sugeno模糊控制器的变型、
非独点模糊逻辑系统、一般Mamdani型模糊系统、
采用线性规则后项的TS型模糊系统、广义模糊系

模糊控制系统讲解29页PPT

模糊控制系统讲解29页PPT

模糊控制系统讲解
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律，就难以成功。
3、道德行为训练，不是通过语言影响 ，而是 让儿童 练习良 好道德 行为， 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体，养 成儿பைடு நூலகம் 自觉的 纪律性 ，这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特

模糊t-s型系统课件

模糊t-s型系统课件
根据实际问题的经验和知识，确定模 糊规则库中的模糊规则。
规则库的建立
根据确定的模糊规则，建立模糊规则 库，包括规则的前提和结论部分。
模糊逻辑推理过程
输入变量的模糊化
将输入变量的精确值转换为模糊集合。
结论推理
根据匹配的模糊规则，进行结论推理，得到 输出变量的模糊集合。
匹配模糊规则
根据输入的模糊集合，匹配模糊规则库中的 模糊规则。
结论与展望
模糊T-S型系统的优势与局限性
01
优势
02
具有较强的鲁棒性和适应性，能够处理不确定性和非线性问题。
能够模拟人类推理过程，实现更接近人类的决策和控制。
03
模糊T-S型系统的优势与局限性
01
局限性
02
对初始条件和参数变化敏感，可能导致系统 性能不稳定。
03
设计和调整过程较为复杂，需要专业知识和 经验。
模糊T-S型系统课件
• 引言 • T-S型模糊逻辑系统的结构 • 模糊T-S型系统的应用 • 模糊T-S型系统的实现 • 结论与展望
01
引言
模糊逻辑与模糊系统简介
01
模糊逻辑是一种处理不确定性、 不完全性知识的工具，它突破了 经典逻辑的局限性，能够更好地 处理现实世界中的复杂问题。
02
模糊系统是基于模糊逻辑的系统 ，它通过模糊化输入和输出，将 不确定性和不精确性引入系统， 从而更好地适应复杂环境。
THANKS
感谢观看
T-S型模糊逻辑系统的基本概念
T-S型模糊逻辑系统是一种常见 的模糊逻辑系统，它由输入变量、 模糊化函数、规则库和去模糊化
函数组成。
T-S型模糊逻辑系统的名称来源 于其创始人，日本学者Tokyo大 学的Sanada教授和Sugeno教

模糊控制3 TS Fuzzy System

2 1 如图5所示，这里 w 和 w 分别代表 L1 和 L2 的权值。
x(k + 1) = ∑ w Ai x(k ) / ∑ w
i i =1 i =1
l
l
i
图5 模糊系统的响应曲线
22
[例5]在上述已知模糊系统中，如果
1.503 −0.588 A1 = 1 0
1 −0.361 A2 = 1 0
S 22：若y(k)是( A2 and C 2 )，则
2 y 22 (k + 1) = (2.256 − 1.120k12 ) y (k ) + (−0.361 − 1.120k 2 ) y (k − 1)
模糊模型的总的输出为
w11 y11 (k + 1) + w12 y12 (k + 1) + w21 y 21 (k + 1) + w22 y 22 (k + 1) y (k + 1) = 17 w11 + w12 + w21 + w22
27
[例6]对于例2中的模糊系统，加入了标准方差为0.5的高斯白噪声， 并假定模型的前提结构和前提参数同原系统相同。采用200组输 入输出数据进行结论参数的辨识，得到如下结果：
28
图8绘出了含有噪声的输入输出数据、原始的结论和辨识 结论。如果这组数据中不含有噪声，那么辨识出来的模 型和原模型完全相同。
图8 原始数据和辨识的结果
29
2、前提参数的辨识
模糊辨识算法中，涉及到3类隶属函数，都是由分段直线组 成的。它们是small, medium, large如下图所示。
图9 3类隶属函数的形式 图9中的 P1 , P2 , , P8 等是前提参数，表示各类隶属函数的 转折点，对应的隶属度是1或0，模糊子集small和large有 2个前提参数待辨识，medium有4个前提参数待辨识。

模糊控制原理完整ppt课件

模糊控制原理
北京理工大学自动化学院 sunjian@ 孙健
第三章 模糊控制原理
模糊控制的基本原理 模糊控制系统的分类 模糊控制器设计 模糊控制的应用
Page 2
第三章 模糊控制原理
Page 3
3.1 模糊控制的基本原理
3.1.1 模糊基本思想
模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础 的一种智能控制方法，它是从行为上模仿人的模糊推理和决策过 程的一种智能控制方法。
确定隶属函数（原则）
模糊化处理方法
人类的控制规则 如果水温比期望值高，就把燃气阀关小； 如果水温比期望值低，就把燃气阀开大。
描述了输入（水温与期望值的偏差 e）和输出（燃气阀开度的增量 u） 之间的模糊关系R
Page 5
3.1 模糊控制的基本原理
模糊值
规则库R
模糊值
模糊化
输入e
输出u
模糊推理
精确值
精确值
期望值 ＋
e A/D
－
温度 传感器
?
为了提高实时性，模糊控制器常常以控制查询表的形式出现。 该表反映了通过模糊控制算法求出的模糊控制器输入量和输 出量在给定离散点上的对应关系。为了能方便地产生控制查 询表，在模糊控制器的设计中，通常就把输入输出的论域定 义为有限整数的离散论域。
Page 11
3.1 模糊控制的基本原理
模糊化
输入量和输出量论域的设计
有关论域的选择问题，一般误差论域m≥6，误差变化 论域n≥6，控制量的论域l≥7。
这是因为语言变量的词集多半选为七个（或八个）这 样能满足模糊集论域中所含元素个数为模糊语言词集 总数的二倍以上，确保模糊集能较好地覆盖论域，避 免出现失控现象。

智能控制课件-模糊控制


0 0 0 0
0 .5 1 .0
0 .5 1 .0
0 .5 1 .0 0 .5 0 .5 0 0
0 0 0 0 0 0 0 .5 0 0 .5 0 .5 0 .5 1 .0 0 0
15
5
模糊决策 模糊控制器的输出为误差向量和模糊关系的合成 合成（ 复合） 合成（复合）
0
0
0
0 0 0 0 0 0 PSe × PSu = 0 × [0 0 0 0 0 0.5 1.0 0.5 0] = 0 1.0 0 0.5 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
自学习、自适应；模糊推理策略；模糊模型辨识；稳定性；硬件实现
3
3.2 模糊控制的基本原理
以模糊集理论 模糊集理论、 模糊集理论 、 模糊语言变量、 模糊语言变量、 模糊逻辑推理为基础，从行为上模 模糊逻辑推理 仿人的模糊推理和决策过程的一种智能控制方法。
3.2.1 模糊控制器的构成
模糊控制器（ Fuzzy Controller—FC ）也称模糊逻辑控制器（ Fuzzy Logic Controller—FLC）。采用模糊理论中模糊条件语句来描述，是一种 语言型控制器，也称模糊语言控制器（ Fuzzy Language Controller-FLC）。 语言型控制器
12
0 0 0 0 0 0 .5 0 0 .5 0 .5 0 .5 1 0 0 .5 1 .0 0 .5 NSe × NSu = 0 × [0 0.5 1 0.5 0 0 0 0 0] = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

模糊控制系统设计PPT课件

A { u 1 ,A ( u 1 ) , u 2 ,A ( u 2 ) , L , u n ,A ( u n ) }
上述“圆块”A的序偶表示为
A { a , 1 , b , 0 . 9 , c , 0 . 4 , d , 0 . 2 , e , 0 }
第9章 模糊控制系统设计
模糊矩阵，μR的取值区间为[0,1]，rij的值也都在[0,1]区间。
当m=n时，称R为n阶模糊方阵；当rij全为0时，称R为零
矩阵，记为0；当rij全为1时，称R为全矩阵，记为E；
当rij只在{0，1}中取值时，称R为布尔矩阵，它对应一个 普通关系。
第9章 模糊控制系统设计
(2) 模糊矩阵的运算 由于模糊矩阵本身是表示一个模糊关系子集，因此根据 模糊集的交、并、补运算定义，模糊矩阵也可做相应的 运算。对于任意两个模糊矩阵R=(rij)m×n，Q=(qij)m×n，则 模糊矩阵的交、并、补运算为
A10.90.40.20 ab c de
第9章 模糊控制系统设计
d
c
U
e
图9.1 论域U中的元素
第9章 模糊控制系统设计
(2) 矢量表示法 如果单独地将论域U中的元素ui（i=1，2，…，n）所对应 的隶属度值µA(ui) 按序写成矢量形式来表示模糊子集A， 则
A (A (u 1 ),A (u 2 ),L ,A (u n ))
1．模糊关系 描述元素之间是否相关的数学模型称为关系，描述元素 之间相关的程度的数学模型称为模糊关系。为了区别于 模糊关系，又称关系为普通关系。显然，模糊关系是普 通关系的拓广和发展，而普通关系可视为模糊关系的特 例，模糊关系是模糊数学的重要组成部分。当论域有限 时，可用模糊矩阵表示模糊关系。模糊矩阵成为模糊关 系的主要运算工具。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当f(x1,x2)的类型取x1和x2的线性函数时，这种推理就称为 T-S型模糊推理。
2、T-S型模糊推理系统
⑴输出函数f(x1,x2)的两种形式 ①0阶T-S型模糊推理： if x1 is A1 and x2 is A2 ,then u=k ②1阶T-S型模糊推理： if x1 is A1 and x2 is A2 ,then u=px1+qx2+r
m
U

wiui
i 1 m
wi

w1u1 w2u2 ...... wmum w1 w2 ...... wm
i 1
⑶计算每条规则权重wi的两种方法 为调节每条规则的权重，常加入一个“认定权重”
的人为因子Ri（设计人员认为第i条规则在总输出中 的权重），对每条规则的权重用Ri进行调节。
⑵按加权平均法（wtaver）计算总输出
①取小法
w1= 0.25；w2= 0.2；w3= 0.375 总输出为：
u3 w1* y1 w2* y2 w3* y3 0.25*17 0.2*24 0.375*15 17.7878
②ห้องสมุดไป่ตู้积法
w1 w2 w3
0.25 0.2 0.375
mf1(x)=1-x/16; mf2(x)=x/60; mf3(x)=1-x/8; mf4(x)=3x/40 试问当测得x1=12且x2=5时，最终输出量u为多少？
解：根据题设，当x1=12且x2=5时
R1： mf1(12)=1-12/16=0.25 mf3(5) =1-5/8=0.375 y1=x1+x2=17
其中： A1 、 A2 ----F集合 k、p、q、r----常数（根据系统的大量输入-输出数据，经过辨识确
定的）
⑵计算系统输出U的两种方法
用n条模糊规则描述系统时，假设一组具体输入的数据xi，它一般会 与多个F集合相关，设激活了m条模糊规则，即
0阶T-S型模糊推理：Ri: if x1 is A1i and x2 is A2i ,then ui=ki 1阶T-S型模糊推理： Ri: if x1 is A1i and x2 is A2i ,then ui=pix1+qix2+ri
（i=1、2、3……n）
当xi激活m条模糊规则时，输出结论将由这m条规则的输出ui决定。
①加权求和法（简称wtsum） 设第i条规则输出的结果为ui，它的权重为wi，则总输出为：
m
U wiui w1u1 w2u2 ...... wmum i 1
其中：wi----第i条规则在总输出中所占分量轻重的比例（权重） ②加权平均法（简称wtaver）
作业：
通过对某系统测试数据的辨识，已经得出描述该系统的 两条T-S模糊规则：
R1: if x1 is F1 and x2 is F3 then y1=0.25-0.3x1+2.5x2; R2: if x1 is F2 and x2 is F4 then y2=1.5+x1+2x2; 模糊子集F1(x)=3-x; F2(x)=x-2; F3(x)=x-4; F4(x)=5-x 求当x1=2.5且x2=4.5时该系统的输出（自行选定认定权重 和计算总输出的算法）。
4.3 T-S型模糊推理
Mamdani模糊推理特点：输出是模糊量→清 晰化处理→清晰量。过程烦琐，并具有随意性， 对模糊量进行数学分析不方便。
1985年，日本学者Takagi和Sugeno提出了 一种新的模糊推理模型----T-S型模糊推理模型。
4.3.1 双输入、单输出系统的T-S型模糊推理模型
实际计算中，常取认定权重Ri=1。 设第i条规则的权重为wi，则 ①取小法
wi Ri A1i x1 A2i x2
②乘积法
wi Ri A1i x1 A2i x2
例：根据某非线性系统输入-输出的大量实测数据，通 过辨识已经得出描述它的三条T-S模糊规则，它们分 别为R1、R2、R3，则有： R1： if x1 is mf1 and x2 is mf3 then y1=x1+x2； R2： if x1 is mf2 then y2=2x1； R3： if x2 is mf4 then y3=3x2。 其中模糊集合mf1、mf2、mf3、mf4的隶属函数， 都可视为简单的直线，分别为：
R2： mf2(12)=12/60=0.2
y2=2x1=2*12=24
R3：
mf4(5)=3*5/40=0.375 y3=3x2=3*5=15
为了计算系统总输出，按照上述方法可有四种不同结论，为了加以区
分，各种组合所得的结果分别用u1、u2、u3、u4表示。 ⑴按加权求和法（wtsum）计算总输出
①取小法
w1=mf1(12)∧mf3(5)=0.25∧0.375=0.25 w2= mf2(12)=0.2 w3=mf4(5)=0.375 总输出为:
u1=w1*y1+w2*y2+w3*y3=0.25*17+0.2*24+0.375*15≈14.675
②乘积法
w1=mf1(12)*mf3(5)=0.25*0.375=0.09375； w2= mf2(12)=0.2； w3=mf4(5)=0.375 总输出为： u2=w1*y1+w2*y2+w3*y3=0.09375*17+0.2*24+0.375*15≈12.0188
w1= 0.09375；w2=0.2；w3=0.375 总输出为：
u4 w1* y1 w2* y2 w3* y3 0.09375*17 0.2*24 0.375*15 17.972 选用不同方法计w算1结w果2 不w同3 ：u1=14.675、0.0u923=7152.001.82、 0u.33=7157.7878、 u4=17.972，取那个值根据具体情况决定。
1、T-S型模糊推理
Mamdani型模糊推理： 大前提：if x1 is A1 and x2 is A2 ,then u is U 小前提：x1 is A1* and x2 is A2*
———————————————————— 结论：u is U*
若系统局部线性、能够进行分段控制时，可改造为：
大前提：if x1 is A1 and x2 is A2 ,then u=f(x1,x2) 小前提：x1 is A1* and x2 is A2* ———————————————————— 结论： u=f(x1*,x2*)