(格利森)弧齿锥齿轮几何尺寸计算
- 格式:xls
- 大小:136.00 KB
- 文档页数:1


弧齿锥齿轮主要参数的测绘计作者: 日期:弧齿锥齿轮主要参数的测绘计算零部件加工部麻俊方弧齿锥齿轮具有承载能力高、运转平稳、噪音低等特点,在汽车行业中得到了广泛的应用。
通常由一对弧齿锥齿轮组成汽车驱动桥主减速器的主要传动机构。
弧齿锥齿轮的设计与测绘计算均比较复杂,下面仅介绍几种主要参数的测绘计算方法。
1.轴交角一对弧齿锥齿轮副的住从动齿轮中心轴线交于一点。
轴线间的交角刀可成任意角度,但在绝大多数汽车驱动桥上,主减速齿轮副都采用90°相交的布置。
2.齿制渐开线锥齿轮的齿制很多,多达40多种,我国常用的齿制有Gleason(格利森)制、Oerlikon(奥利康)制、Kingelnberg(克林贝格)制三种。
其中应用最广泛也是最常见到的是Gleaso n(格利森)制弧齿锥齿轮。
不同的齿制,对应不同的参数计算方法与计算公式,在测量齿轮时一定要注意区分。
3•模数弧齿锥齿轮模数是一个变值,由大端向小端与锥距成比例缩小,通常以大端面模数叫来计算。
GB12368-9C规定了锥齿轮大端端面模数,其中以》1为例,有1、1.125、1.375、1.5、1.75、2等等。
但是所测量的齿轮模数不一定为整数,也不一定符合标准模数系列。
对于模数的测绘与计算,有以下方式:1. 由测量的锥距R,可初步估算锥齿轮的大端模数 叫h(用深度尺来测量)加以复核。
对于等顶隙收缩齿(格里森制),齿顶高系数ha = 0.85,顶隙系*数C *=0.188则齿高 h=(2 ha +C *)m 。
*由此得出模数m=h(2ha +C *),进而复核模数m s 。
tm s—2.测量出锥齿轮的周节t ,根据公式 来进行计算,这种方法要求测量数据准 确无误,且被测绘齿轮无磨损现象。
3. 由齿顶圆直径反求模数。
首先测绘出齿顶圆的直径尺寸,利用齿顶圆计算公式,然 后反求模数。
所使用的反求公式为4. 由刀顶距的数值计算模数。
弧齿锥齿轮铣刀盘的刀顶距W 叫席2式中ms—大端模数的估算数值;1 0.5— L e ;R因为2 Z2 ^ 、、, ,于是便可确定锥齿轮大端模数m 2R人『云。

弧齿锥齿轮计算范文1.基本概念:-弧齿锥齿轮:是一种带有锥面的圆锥形齿轮,在用于传动时,锥齿轮的啮合点在轴心线上。
-基本参数:包括齿数、模数、齿顶高系数、齿根高系数等。
-啮合角:两个齿轮齿廓线的交线与轴线间的夹角。
2.弧齿锥齿轮计算的基本公式:-模数m:弧齿锥齿轮齿数与模数的比值。
-齿距p:两个邻齿间的同心圆周弧长。
-齿厚s:齿顶与齿底之间的距离。
-齿顶高h_a:从齿顶到基圆的距离。
-齿根高h_f:从齿底到基圆的距离。
-齿顶宽b:两齿轮在法向上的接触宽度。
-(注:以上参数表示的是单齿齿轮的大小)3.弧齿锥齿轮计算的步骤:a.齿轮参数的确定:确定需求参数,如传递功率、转速比、传动效率、齿轮种类等。
b.模数的选择:应满足传递功率与转速的要求,并考虑加工性与强度。
c.齿数及啮合角的计算:使用基本公式计算齿数和啮合角。
d.齿顶高和齿根高的计算:使用基本公式计算齿顶高和齿根高,考虑强度。
e.齿轮啮合宽度的计算:使用齿顶高和齿根高计算齿轮啮合宽度,与承载能力有关。
f.齿轮等效齿数的计算:计算齿轮的等效齿数,以确定传动比。
g.法向变位系数及挤压系数的计算:根据实际情况计算法向变位系数及挤压系数,控制齿轮传动质量。
h.齿轮加工校核:计算齿轮加工校核参数。
i.绘制齿轮图样:根据以上计算结果,绘制齿轮尺寸图样。
弧齿锥齿轮计算涉及到多个参数和公式的运用,需要根据实际情况进行具体的计算和校核。
以上给出的步骤和基本公式只是一个简单的概述,实际计算中还需要考虑更多的因素,如弯曲应力、接触应力、表面质量等。
因此,在实际应用中,建议根据实际情况进行具体的计算和校核,确保齿轮传动的正常运行。

弧齿锥齿轮几何参数设计1第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念 14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则 «Skip Record If...»大小轮的齿数之比称为锥齿轮的传动比«Skip Record If...» (14-1)小轮和大轮的节点半径r 1、r 2分别为«Skip Record If...» «Skip Record If...»(14-2) 它们与锥齿轮的齿数成正比,即«Skip Record If...»(14-3) 传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为图14-2 锥齿轮的节锥与节面图14-1 弧齿锥齿轮副«Skip Record If...» «Skip Record If...»(14-4)当«Skip Record If...»时,即正交锥齿轮副,«Skip Record If...» 14.1.2弧齿锥齿轮的旋向与螺旋角1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图14-3)。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮(图14-3b ),逆时针倾斜者则为左旋齿(图14-3a )。

圆弧齿锥齿轮计算公式(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=ar ctg(hf2/R)10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)11顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm22端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1 +Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=23齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分。

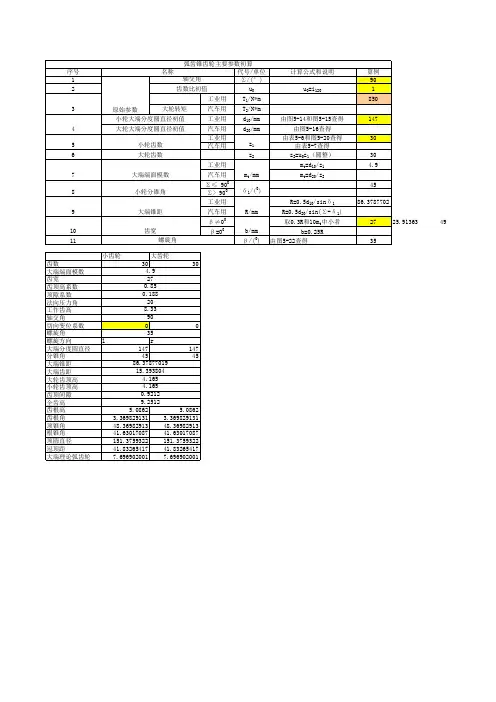


锥齿轮传动计算卡编号:16(弧齿锥齿轮)产品型号:订货号:10026零件件号:①30201②30202计算人 :计算日期:注:“度.分秒”标注示例 — 56.0638 表示56度6分38秒;35.596 表示35度59分60秒(即36度)。
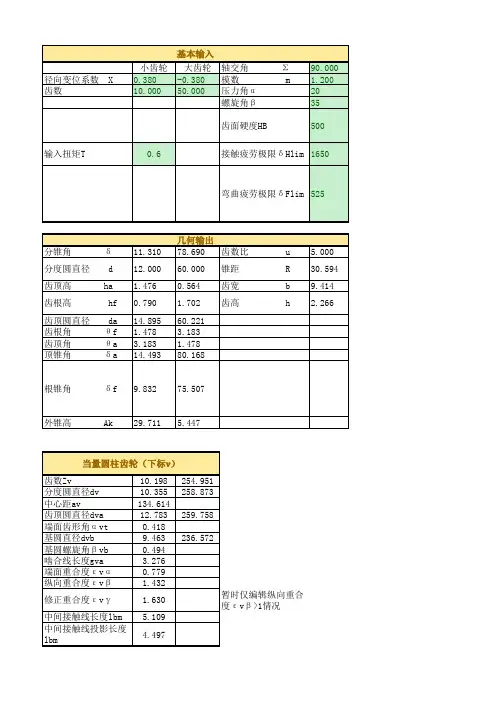
项目①小轮②大轮几何参数:旋 向右 旋左 旋齿数Z1324大端端面模数m7.5毫米轴交角Σ90度法向压力角αn20度中 点 螺 旋 角βm39度齿宽b30毫米全齿高系数x t 1.888工作齿高系数x w 1.7顶隙 系 数c0.188高度变位系数x0.2756-0.2756切向变位系数x s0.0069-0.0069分度圆直径d97.5毫米180毫米外锥距Ra102.3551毫米毫米分度圆锥角δ28.2635度.分秒61.3325度.分秒顶锥角(等顶隙)δa33.5627度.分秒64.4516度.分秒根锥角δf25.1444度.分秒56.0333度.分秒齿顶高h a8.442毫米 4.308毫米齿根高h f 5.718毫米9.852毫米全齿高h t14.16毫米毫米工作齿高h12.75毫米毫米大端分度圆理论弧齿厚Sa13.893毫米9.669毫米大端顶圆直径d a112.346毫米184.104毫米分锥顶点至轮冠距离A k85.979毫米44.962毫米大端法向弦齿厚S n9.701毫米(单号单面切削法) 6.893毫米大端法向弦齿高H n8.276毫米 4.224毫米重合度ε总 1.714ε纵向 1.221ε端面 1.203较小!大 端 螺 旋 角βa43.0453度.分秒小 端 螺 旋 角βi35.522度.分秒刀盘名义直径选定值Dc190.5毫米公差值:(按 GB11365--89 锥齿轮和准双曲面齿轮精度)精度等级Ⅰ:7Ⅱ:6Ⅲ:6最小法向侧隙种类c法向侧隙公差种类C图样标 注7-6-6c GB 11365--89齿厚上偏差Ess-0.053毫米-0.072毫米齿厚下偏差Esi-0.123毫米-0.167毫米齿厚公差Ts0.07毫米0.095毫米最小法向侧隙jn min0.074毫米最大法向侧隙jn max0.318毫米切向综合公差F'i0.052毫米0.072毫米一齿切向综合公差f'i0.016毫米0.019毫米齿距累积公差F P0.045毫米0.063毫米齿距极限偏差±f pt0.013毫米0.014毫米齿形相对误差的公差f c0.006毫米0.008毫米接触斑(沿齿长)50% 至70%(沿齿高)55% 至75%轴交角极限偏差±EΣ(齿宽中点处的线值)0.032毫米齿坯顶锥母线跳动公差0.025毫米0.03毫米基准端面直径25毫米320毫米齿坯基准端面跳动公差0.025毫米0.015毫米齿坯轮冠距极限偏差-0.075毫米-0.075毫米齿坯顶锥角极限偏差8分8分齿坯尺寸公差轴径IT5GB 1800--79孔径IT6GB 1800--79外径尺寸极限偏差上偏差0下偏差-IT8GB 1800--79承载能力:名义转矩T 250N·m461.54N·m 名义功率P 26.18kW48.33kW 小 轮转速n1000r / min541.67r / min 材质合金钢渗碳淬火支 承 形 式一个是两端支承,另一个是悬臂许用接触应力ζHP1249.99N/mm21249.99N/mm2计算接触应力ζH765.75N/mm2765.75N/mm2接触强度安全系数S H 2.04 2.04许用齿根应力ζFP795.79N/mm2787.75N/mm2计算齿根应力ζF180.16N/mm2175.11N/mm2弯曲强度安全系数S F 3.35 3.41结论意见: ·安全系数过大,造成浪费!·重合度过小!·大端螺旋角大于小端螺旋角,无反向收缩。
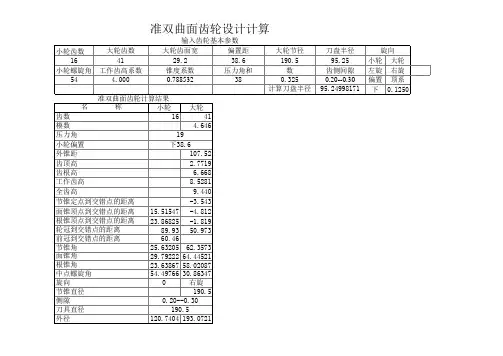
孤齿锥齿轮传动的几何参数计算
高荣元
【期刊名称】《钢铁厂设计》
【年(卷),期】1996(000)004
【摘要】本文叙述格里森孤齿锥齿轮传动参数的选择和几何尺寸的计算。
【总页数】5页(P19-23)
【作者】高荣元
【作者单位】无
【正文语种】中文
【中图分类】TH132.41
【相关文献】
1.汽车后桥主传动锥齿轮滚切修正切齿调整计算方法 [J], 卢明文;翟庆富
2.内齿行星传动内齿轮副的几何参数计划 [J], 任工昌;王乃信
3.双重收缩齿直齿锥齿轮的几何计算和加工 [J], 高旭;周湘衡
4.实现动平衡的内齿行星齿轮传动的几何参数分析及参数化建模 [J], 陶静;郑甲红
5.直齿锥齿轮传动的几何参数计算 [J], 高荣元
因版权原因,仅展示原文概要,查看原文内容请购买。
第14章弧齿锥齿轮的轮坯设计14.1弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副 的形式如图14-1所示,与直齿锥齿轮相比, 轮齿倾 斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的 节锥一样,相当于一对相切圆锥面作纯滚动,它是 齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的 (图14-2 )。
两个相切圆锥的公切面成为齿轮副的 节平面。
齿轮轴线与节平面的夹角,即节锥的半锥 角称为锥齿轮的节锥角1或2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角 。
节锥任意一点到节锥顶点0的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则1 2大小轮的齿数之比称为锥齿轮的传动比i 12 亞(14-1)Z 1小轮和大轮的节点半径「1、「2分别为它们与锥齿轮的齿数成正比,即「 2sin 2 Z 2 r 1 sin 1z 1传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为,i 12 s intg2当900时,即正交锥齿轮副,tg 2 i 1214.1.2弧齿锥齿轮的旋向与螺旋角1 .旋向弧齿锥齿轮的轮齿对母线的倾斜方向 称为旋向,有左旋和右旋两种(图14-3 )。
面对轮齿观察,由小端到大端顺时针倾斜r-i Rsin 1r 2 Rsin 2(14-2)(14-3)(14-4)图14-1弧齿锥齿轮副(a )左旋(b )右旋者为右旋齿轮(图14-3b ),逆时针倾斜者则为左旋齿(图14-3a )。
大小轮的旋向相反时,才能啮合。
一般情况下,工作面为顺时针旋转的主动锥齿轮的螺旋方向为左旋,被动轮为右旋(图14-1);工作面为逆时针旋转的,情况相反。
这样可保证大小轮在传动时具有相互推开的轴向力,从而使主被动轮互相推开以避免齿轮承载过热而咬合。
2 .螺旋角弧齿锥齿轮轮齿的倾斜程度由螺旋角i来衡量。
弧齿锥齿轮纵向齿形为节平面与轮齿面相交的弧线,该弧线称为节线,平面齿轮的节线称为齿线。
ug格利森弧齿准双曲面齿轮参数【ug格利森弧齿准双曲面齿轮参数】1. 引言在工程领域中,齿轮传动一直扮演着至关重要的角色。
而在齿轮传动中,准双曲面齿轮因其传动精度高、传动效率高等特点,被广泛应用于各个领域。
而ug格利森弧齿准双曲面齿轮参数的设计与研究,则是提高准双曲面齿轮传动性能的关键。
2. ug格利森弧齿准双曲面齿轮参数概述ug格利森弧齿准双曲面齿轮参数是指根据准双曲面齿轮的设计原理和要求,利用ug软件进行齿轮参数的设计和优化。
ug软件以其强大的建模和仿真功能,可以帮助工程师更好地理解和设计准双曲面齿轮的参数,从而提高齿轮传动的性能和可靠性。
3. 深入探讨ug格利森弧齿准双曲面齿轮参数在ug软件中,通过设定齿轮的模块、齿数、法向压力角、顶隙系数等参数,可以实现对准双曲面齿轮的精确建模。
而通过对齿轮参数的调整和优化,可以使得齿轮的传动效率得到提高,传动噪音得到降低,从而满足不同工程应用的需求。
4. ug格利森弧齿准双曲面齿轮参数的应用在实际工程中,ug格利森弧齿准双曲面齿轮参数的应用范围非常广泛,涉及到机械、航天、汽车等多个领域。
在航天领域,ug格利森弧齿准双曲面齿轮参数的优化设计可以大大提高航天器的传动性能,增强其在特殊环境下的可靠性。
在汽车领域,ug格利森弧齿准双曲面齿轮参数的应用可以提高汽车变速器的传动效率,降低磨损和噪音,延长使用寿命。
5. 总结与展望通过对ug格利森弧齿准双曲面齿轮参数的深入研究和应用,可以进一步拓展准双曲面齿轮在工程领域中的应用范围,提高其传动性能和可靠性。
未来,随着工程技术的不断发展和ug软件功能的不断完善,ug格利森弧齿准双曲面齿轮参数的设计和优化将更加高效和精确。
希望不断有更多的工程师和研究人员投入到ug格利森弧齿准双曲面齿轮参数的研究和应用中,为齿轮传动技术的发展贡献力量。
个人观点:ug格利森弧齿准双曲面齿轮参数的设计与研究是齿轮传动技术发展的重要方向。
通过对参数的深入理解和优化,可以提高准双曲面齿轮的传动性能,满足不同工程领域的需求。
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比,即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时,即正交锥齿轮副,122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图14-3)。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮(图14-3b ),逆时针倾斜者则为左旋齿(图14-3a )。
大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-3 弧齿锥齿轮的旋向图14-1 弧齿锥齿轮副反时,才能啮合。
一般情况下,工作面为顺时针旋转的(从主动轮背后看,或正对被动轮观察),主动锥齿轮的螺旋方向为左旋,被动轮为右旋(图14-1);工作面为逆时针旋转的,情况相反。
ug格利森弧齿准双曲面齿轮参数
【最新版】
目录
1.介绍 Ug 格利森弧齿准双曲面齿轮
2.详述 Ug 格利森弧齿准双曲面齿轮的参数
3.分析 Ug 格利森弧齿准双曲面齿轮的应用和优势
正文
一、介绍 Ug 格利森弧齿准双曲面齿轮
Ug 格利森弧齿准双曲面齿轮,是一种在工程领域中广泛应用的齿轮类型。
其独特的设计使其在传动过程中具有较高的承载能力和稳定性,因此受到了许多行业的青睐。
二、详述 Ug 格利森弧齿准双曲面齿轮的参数
1.齿数:这是 Ug 格利森弧齿准双曲面齿轮的一个重要参数,决定了齿轮的大小和传动比。
2.模数:模数是描述齿轮大小的参数,它决定了齿轮的齿高和齿厚。
3.压力角:压力角是描述齿轮齿形的参数,它影响了齿轮的强度和传动性能。
4.中心距:中心距是描述齿轮轴间距的参数,它影响了齿轮的安装和使用。
5.齿面硬度:齿面硬度是描述齿轮齿面耐磨性的参数,它影响了齿轮的使用寿命。
三、分析 Ug 格利森弧齿准双曲面齿轮的应用和优势
Ug 格利森弧齿准双曲面齿轮在许多行业中都有应用,如汽车、机床、船舶等。
其优势主要体现在以下几个方面:
1.高承载能力:由于其独特的设计,使得 Ug 格利森弧齿准双曲面齿轮在传动过程中具有较高的承载能力。
2.高稳定性:Ug 格利森弧齿准双曲面齿轮的设计使其在传动过程中具有较高的稳定性,能够保证传动的准确性和平稳性。
3.高效率:Ug 格利森弧齿准双曲面齿轮的齿形设计使其在传动过程中具有较高的效率,能够降低能耗。
4.长使用寿命:Ug 格利森弧齿准双曲面齿轮的齿面硬度高,使其在传动过程中具有较长的使用寿命。