心理测量学复习_常模
- 格式:doc
- 大小:98.00 KB
- 文档页数:4
心理测量学——第二节测验常模的类型最简单最基本的表示常模的方法是转换表,有时也叫常模表。
常模分数的表示方法:转换表法、剖面图法智力测验①测试过程必须使用正规16PF问题和答卷纸,不得随意修改,对被试的指导语不得超过允许范围②测题都是关于个人的兴趣和态度。
测题没有对错之分③被试必须首先做四个例题,被试必须在掌握了答题方式之后,方可正式测试④要按手册规定的程序和方式实施标准得分分析: 1.中间型:T43.3--56.7 普通占50.0 2.倾向型:T38.5--43.3 倾低占12.5 T56.7--61.5 倾高占12.53.典型型:<38.5 特低占12.5 >61.5 特高占12.51.典型的外向(E分特高)爱交际,喜参加联欢会,朋友多,需要有人同他谈话,不爱一人阅读和作研究,渴望兴奋的事,喜冒险,向外发展,行动受一时冲动影响。
喜实际的工作,回答问题迅速,漫不经心,随和,乐观,喜欢谈笑,宁愿动而不愿静,倾向进攻。
总的来说是情绪易失控的人,不是一个很踏实的人。
2.典型内向(E分特低)安静,离群,内省,喜爱读书而不喜欢接触人。
保守,与人保持一定距离(除非挚友),倾向于事前有计划,做事观前顾后,不凭一时冲动。
不喜欢兴奋的事,日常生活有规律,严谨。
很少有进攻行为,多少有些悲观。
总得说是个比较踏实可靠的人,其价值观念是以伦理道德为标准。
3.典型情绪不稳(N分特高)焦虑,紧张,易怒,往往又有抑郁。
睡眠不好,患有各种身心障碍。
情绪过分,对各种刺激的反应都过于强烈,情绪激发后又很难平复下来。
由于强烈的情绪反应而影响了他的正常适应。
不可理喻,甚至有时走上危险道路。
在与外向结合时,这种人是容易冒火的,和不休息的,以至激动,进攻。
概括地说,是一个紧张的人,好抱偏见,以至错误。
4.情绪稳定(N分很低)倾向于情绪反应缓慢、微弱,即使激起了情绪也很快平复下来,总得说是个生活有节制的人,喜欢过平静生活的人。
5.P分高的成人独身,不关心人。


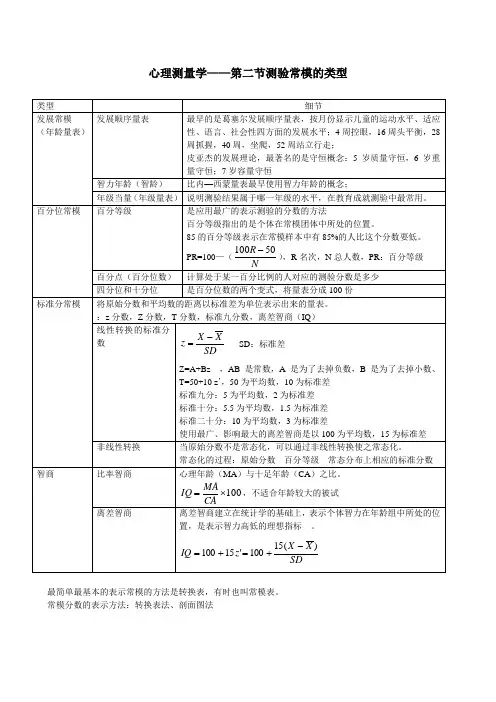
心理测量学:测验的常模之常模的类型:㈠发展常模(又称年龄量表):⑴发展顺序量表:①葛塞尔发展程序量表(发展顺序量表最早的一个范例。
16周能使头保持平衡,28周能用手抓握东西并把玩,40周能控制躯干、坐立、或爬行,52周能控制腿脚运动、站立和行走)②皮亚杰的守恒概念(5岁理解质量守恒,6岁掌握重量守恒,7岁有容量守恒)⑵智力年龄(又称智龄。
吴天敏的比内-西蒙量表智龄的计算方法:6岁+4×2月+3×2月+2×2月=7岁6个月)⑶年级当量(又称年级量表。
在教育成就测验中最常用。
)㈡百分位常模:⑴百分等级:是应用最广的表示测验分数的方法。
一个测验分数的百分等级是指在常模样本中低于这个分数的人数百分比,百分等级指出的是个体在常模团体中所处的位置,百分位等级越低,个体所处的位置就越低。
未分组资料百分等级计算公式PR=100-(100R-50)/N。
⑵百分点:在分数量表上,相对于某一百分等级的分数点就叫百分点或百分位数。
百分点的计算根据直线内插法(例见P341)。
⑶四分位数:是将量表分成四等分,相当于百分等级的25%、50%和75%对应的三个百分分成的四段。
⑷十分位数:1%~10%为第一段,91%~100%为第十段。
㈢标准分常模:⑴线性转换的标准分数:z分数为最典型的线性转换的标准分数z=(X-)/SD,转换公式Z=A+Bz⑵非线性转换的标准分数:当原始分数不是常态分布时也可以是使之常态化,这一转换过程就是非线性的。
转换为T分数T=50+10。
标准九分是以5为平均数,以2为标准差的一个分量表,最早广泛应用于美国空军和某些教学情境中的分级。
标准十分平均数为5,标准差为1.5;标准二十分平均数为10,标准差为3。
单纯用心理年龄来表示智力的高低的方法缺乏不同年龄儿童间的可比性,因此一般都用比率智商和离差智商来表示智力的高低。
⑴比内-西蒙量表由美国斯坦福大学推孟教授于1916年对其修订而成斯坦福-比内量表,其中以比率智商(IQ)表示结果IQ=MA/CA×100IQ等于100代表正常,高于100代表发展迅速,低于100代表发育迟缓。





一、测量与心理测量⏹重要概念1.测量:测量是根据法则给予事物分派数字(Stevens S S,实验心理学手册,1951)亦即依据一定的法则使用量对事物的特征进行定量描述的过程。
2.测量的三要素事物的属性(测什么?)、法则、规则(如何测?即测量原理)、数字(测量结果)3.心理测量(1)一般的定义:对心理特点(或心理学概念)的测量;(依据一定的心理学和教育学理论,使用测验对人的心理特质和教育成就进行定量描述的过程)(2)课本:根据一定的心理学理论,使用测验对人的心理特质进行定量描述的过程;(3)心理测量学的定义:布朗的定义:是指对一个行为样本进行测量的系统程序;安娜斯塔西的定义:实质是对行为样本的客观可标准化的测量;(4)一种动作、过程;或是实施一组项目。
心理测量就是根据一定的法则用数字对人的行为加以确定。
即根据一定的心理学理论,使用一定的操作程序,给人的行为确定出一种数量化的价值。
4.心理测验:进行心理测量的工具,其形式一般为一组题目与相应的评分标准。
工具,包括问卷、测验、面试、评价中心等;或是一组项目心理测验就是通过观察人的少数有代表性的行为,对贯穿在人的全部行为活动中的心理特点作出推论和数量化分析的一种科学手段,是心理测量的一种工具和手段,是根据一定法则对人的行为用数字加以确定的方法。
5.心理评估:更全面的测量,包括使用观察、访谈的方法获得有关信息。
6.行为样本:心理测量的理论取向,即认为心理测量是对有代表性的部分行为进行测量。
课本定义:从大量行为中抽取与欲测量的心理特质直接相关的一组行为进行测量,并依据对这一组行为的测量结果推断其心理特质。
这一组被抽取出来的、作为直接的测量对象的行为就是行为样本。
内在要求:①在测量和界定特定属性的行为时,心理测验并非要测量所有可能出现的行为;②一个测验的质量主要是由样本的代表性所决定。
7.标准化,即统一化,统一规格,一般指产品设计的各个方面测量标准化,主要指测验使用时的统一化,包括4个方面,可以考试为例;而测验(测量工具,主要是问卷)本身由于比较简单,因而无所谓标准化8.个别测验:同一主试在同一时间内只能测量一个被试的测验p149.团体测验:同一被试在同一时间能够测量许多被试的测验p14⏹思考题:1...试述心理测量的特点?P8(1)首先,心理测量依据的法则在相当一定程度上是一种理论,很难达到如同物理测量依据的法则那样普遍被研究者共同接受的科学水平;(2)其次,心理测量的对象是人的心理特质和教育成就;(3)再次,心理测量的量尺是由有关领域的专家经过长期的编制、试用、修订、完善而逐渐形成的标准化测验,它的编制是一项高度专门化的系统工作,要达到科学所要求的水平绝非易事;(4)最后,心理测量的目标虽然是人的心理特质和教育成就进行定量分析,但这种定量分析的精确度远不及物理测量的精确度。



心理测量学复习内容一、名词解释:常模、投射测验、内容效度、随机样本、 27%规则、常模参照测验、标准参照测验、反应定势、复本信度、测量误差、项目分析、自我效能感、压力访谈、巴纳姆效应、弗林效应、索恩迪测验、心理年龄、比率智商、离差智商、项目特征曲线、智力的PASS二、问答题:1、经典测验理论有哪些局限性?2、比内之后心理测验的迅速发展主要体现在哪些方面?3、按测验的人数分心理测验可以分成哪几类,各有什么优缺点?4、心理测验编制的一般程序是什么?5、如何做到测验使用的标准化?6、简述心理测验的性质。
7、表面效度和内容效度的区别。
8、原始分数为什么要转化为导出分数?9、影响测验效度的特殊因素有哪些?这些因素是如何影响测验的效度的?10、、简述项目反应模型的特征。
11、心理测量工作者应遵循哪些伦理道德原则?12、简述测验的信度与效度之间的关系。
13、投射测验技术的理论基础以及它的优缺点,并指出在何种情况下选用这种方法更合适?14、科学心理测验的奠基人(高尔顿、卡特尔、比纳)分别的简介及贡献15、心理测评中被试的需要有哪些?16、什么是误差?误差分为哪几类?17、影响信度的因素有哪些?18、离差智商分数优于比率智商分数的原因?三、论述题1、试比较几种常用的人格测验:MMPI、16PF、EPQ?2、试述成就测验与能力倾向测验、智力测验的区别。
3、结合韦氏智力量表的结构、记分及应用,请对其优缺点进行简要评价。
4、试论心理测量的间接性?5、人格测验目前存在的问题主要有哪些?6、人格理论研究中特质理论、精神分析理论、人本主义理论以及社会学习理论,哪一种理论对人格评估的贡献最大?从理论的解释力和与你自己的人格理论的一致性程度来看,哪种理论对你更有吸引力,为什么?7、试着为相面术和笔迹学作合理的人格评估手段进行辩护。
为什么它们的名誉要好于颅相学和占星术?8、试着对受审能力和精神失常这两个法律概念进行区分。
哪些心理评估工具或技术可以协助做出有关受审能力和精神失常的判断?四、常用量表:他们各自编制的目的,应用范围、特点、内容、施测的注意事项是什么?1、常用症状评定量表;康奈尔医学指数(CMI)、SCL-90、自评抑郁量表和焦虑量表、汉密尔顿抑郁量表和焦虑量表2、智力量表:比纳-西蒙智力量表、斯坦福-比纳智力量表、韦克斯勒智力量表、瑞文测验3、人格测验:MMPI、16PF、EPQ、罗夏墨迹、主题统觉五、计算题。
心理咨询师考试心理测量学知识:测验
的常模(一)份
心理咨询师考试心理测量学知识:测验的常模 1
第一单元
一、常模团体的'性质
常模团体:是由具有某种共同特征的人所组成的一个群体,或者是该群体的一个样本
对测验编制者而言,常模的选择主要是基于对测验将要施测的总体的认识
常模团体必须能够__该总体,包括:确定一般总体、确定目标总体、确定样本
二、常模团体的条件
(一)群体的构成必须明确界定
(二)常模团体必须是所测群体的__性样本
(三)样本的大小必须要适当:在实际工作中,应从经济的或实用的可能性和减少误差这两方面来综合考虑样本的大小最低:不小于30或100个
全国性常模应有2000~3000人为宜
(四)标准化样组是一定时空的产物(具有新进性)
三、取样的方法
取样即从目标人群中选择有__性的样本
抽样方法:
(一)简单随机抽样:按照随机表顺序选择被试构成样本
(二)系统抽样:要求无序可排,也无等级结构存在
K为组距:K=N�Mn
121名学生中取40人作为样本__
则K=121�M40;K=3;所以3人为一段,可分40段,每段取一人
(三)分组抽样:总体数目大,且群体又有多样性,先将群体进行分组,再在组内进行随机取样
(四)分层抽样:在确定常模时,最常用的方法
又可分:分层比例抽样和分层非比例抽样
四、常模分数与常模
(一)常模分数:是施测常模样本被试后,将被试者的原始分数按一定规则转换出来的导出分数
导出分数具有一定的参照点和单位,是一个有意义的测验量表,它与原始分数等值,可以进行比较
(二)常模:是常模分数构成的分布,是解释心理测验分数的基础。
心理咨询师心理测量学考点归纳一、关键信息1、心理测量学的基本概念与定义名称:____________________________描述:____________________________2、常见心理测量工具工具名称:____________________________适用范围:____________________________特点:____________________________3、心理测量的信度与效度信度的定义:____________________________信度的评估方法:____________________________效度的定义:____________________________效度的评估方法:____________________________4、心理测量的常模常模的概念:____________________________常模的类型:____________________________常模的制定方法:____________________________5、项目分析难度:____________________________区分度:____________________________项目分析的方法:____________________________6、心理测量的误差来源误差类型:____________________________控制误差的方法:____________________________二、心理测量学的基本概念与定义11 心理测量的含义心理测量是依据一定的心理学理论,使用一定的操作程序,给人的能力、人格及心理健康等心理特性和行为确定出一种数量化的价值。
111 心理测量的特点心理测量具有间接性、相对性和客观性。
112 心理测量与心理测验的区别心理测量是一个更广泛的概念,包括了心理测验以及其他评估心理特性的方法;而心理测验是一种标准化的测量工具和程序。
心理测量学常模名词解释嘿,你知道吗?心理测量学常模这词儿听起来就挺高大上的,其实没那么玄乎。
就好比咱去买衣服,有个标准尺码表一样。
比如说我上次去买牛仔裤,那店员拿了个尺码表出来,上面写着不同的腰围、臀围对应的尺码,什么 28 码、30 码的。
这尺码表呢,就是根据大多数人的身材数据统计出来的一个大概的标准,心理测量学常模也有这么点意思。
我记得我上中学的时候啊,学校组织了一次心理测试。
那测试题一道道的,可多了。
做完之后呢,就会有个结果出来。
当时我就纳闷了,这结果是咋得出来的呢?后来才知道,这心理测量学常模就在其中起作用了。
它就像是一把尺子,把我们这些学生在测试中的表现和其他很多同年龄段、同背景的人的数据进行比较。
比如说,在关于焦虑程度的测试里,如果大部分同年龄段的学生平均得分是 30 分,而我得了40 分,那就说明我相对来说可能比较焦虑。
这常模就是把我们的个人数据放在一个大群体里去衡量,看看我们处于啥水平。
再打个比方吧,就像我们在学校里考试排名。
全班同学的成绩有个平均分,还有个排名情况。
这个平均分和排名的概念就有点像心理测量学常模。
它能让老师知道每个学生在班级里的学习水平位置。
心理测量学常模也是这样,不过它衡量的不是学习成绩,而是各种心理特质,像性格特点、智力水平、情绪状态等等。
常模的建立可不容易,就像制作那个衣服尺码表,得收集好多好多人的身材数据才行。
心理测量学常模得找大量的不同类型的人去做各种心理测试,然后把这些数据整理分析,找出其中的规律和平均值,这样才能形成一个有参考价值的常模。
要是没有这个常模,那心理测试的结果就只是孤零零的一个数字,我们根本不知道它代表啥,是好是坏,是正常还是不正常。
所以说,心理测量学常模就像是心理测试世界里的导航仪,指引着我们去理解那些测试数据背后的意义,让我们能大概知道自己在人群中的心理状态处于啥位置,就像知道自己在买衣服时该选啥尺码一样重要呢。
为什么要有常模?
没有另外的解释资料,任何心理测验的原始分数都是毫无意义和价值的。
要使原始分数具有价值,就需要有一些参照数据。
心理测验分数的解释,通常是参照常模进行的。
什么叫常模(norm)?
常模分数与常模
1.常模分数:就是施测常模样本被试后,将被试者的原始分数按一定规则转换出来的导出分数。
导出分数与原始分数等值,有意义、等单位、带参照点。
2.常模:常模分数(导出分数)构成的分布就是通常所说的常模,即常模团体或样本的标准化的得分分布。
它是解释心理测验分数的基础。
什么是原始分数(raw score)?什么是导出分数?
被试在接受检验后,根据测验的计分标准,对照被试的反应所计算出的测验分数称作原始分数。
但是原始分数不能直接反应出被试之间的差异状况,也不能说明被试在其他等值测验上应获得什么样的分值。
为了是原始分数本身具有意义,使不同测验的分数可以相互比较,就必须将原是分数转换为导出分数。
导出分数就是在原是分数转换的基础上,按照一定的规则,经过统计处理后获得的具有一定参考点和单位,且可以相互比较的分数。
什么叫常模团体(norm group)?
1.定义:常模团体是由具有某种共同特征的人所组成的一个群体,或者是该群体的一个样本。
2.条件:(1)构成必须明确界定:样本所有成员是同质的且界限清晰,必须是所测群体的代表
性样本,构成和得分分布与总体尽量吻合。
(2)注意常模的时效性。
(3)样本的大小要适当:如果总体数目大,相应的样本也大,一般最低不小于30或
100个。
全国性常模,一般应有2000到3000人为宜。
3.取样方法
取样即从目标人群中选择有代表性的样本。
(1)简单随机抽样(random sampling):按照随机顺序表选择被试作为样本;或者是将抽样范
围中的每个人或者每个抽样单位编号,随机选择。
(2)系统抽样:有时在总体数目为N的情况下,若要选择K分之一的被试作为样本,则可
以在抽样范围内选择第K个人来构成样本。
K为组距:K=N/n
(3)分组抽样:有时总体数目较大,无法编号,而且群体又具有多样性,可先将群体分为
一定的小组,再从小组内随机抽样。
(4)分层抽样(stratified random sampling):最常用的是分层抽样方法。
它是先将目标群体一
某种变量(如年龄)分成若干层次,再从各层次
中随机抽取若干个案。
使各层次差异显著,同层
次保持一直,增加了样本的代表性。
常模类型有哪些?
智力年龄(mentle age)、百分等级(persontile rank)、百分点(persontiles)、标准分(standard scores),如Z分数(standard score)、T分数(T score)、离差智商、标准九分、标准十分等
1.智力年龄
比奈-西蒙量表中首先使用智力年龄的概念。
可作为评价儿童智力发展水平的年龄量
表。
儿童在年龄量表所得分数,能代表他的智力水平的年龄。
这种分数叫做智力年龄也称:智龄。
假如某儿童6岁组的题目全部通过,7岁组通过4题,8岁组通过3题,9岁组通过2 题,其智龄为:6(岁)+4×2(月)+3×2(月)+2×2月=6岁+18月=7岁6个月
2.百分等级(percentile rank)
定义:
某一个原始分数的百分等级,就是指团体中在该分数以下的分数(或被试)的百
分比。
用符号 PR 表示。
学生甲测验分数的百分等级是88,就是指低于甲分数的学生占测验对象总体的88%,高于甲分数的学生占12%。
计算:
a.未分组的数据
对于未分组的数据求一个原始分数的百分等级,可先将被试团体的全体原始分
数从大到小排序,然后采用下列公式计算:
式中,P R 为百分等级,R 为排名,N 为被试总人数。
例如,某被试在一次由50人参加的侧严中得80分,排名第九,则该生成绩的
百分等级为:
其百分等级为83,即比80分低的原始分数占全体得分的83%,比其高的只占17%。
b.已分组的数据
如果被是团体较大,往往以对分数做过初步整理,分数资料通常以次数分布
表的形式呈现,此时可采用下列公式求得百分等级:
式中X 为被试原始分数,L 为X 所在组下限,f 为X 所在组的次数,F b 为X
所在组一下各组次数之和,i 为组距,P R 为百分等级,N 为被试总人数。
c.此外,还有公式:
c f L 为低于 x 的分数出现次数;
f i 分数 x 的出现次数;
N 为参加和完成测验的总人数
百分位數是用標準化樣本在某一特定原始分數以下所佔的人數百分比來表示,可
看出受試者在團體中的相對位置。
優點:1.易計算、易了解。
2.能做比較,故使用廣泛。
缺點:單位大小不一,越靠近分配的兩端,單位的不等性越明顯。
所以它只能指出某人在常態樣本下的相對位置,並不能說出兩個百分位數的差距。
1005.0⨯+=N f
cf PR i L x
2.百分点(百分位数):
与百分等级的计算方法正好相反。
例如:高考的最高分为695分,其百分等级为100,最低分为103分,百分等级为1,要录取20%的学生进入大学,百分等级为80的百分位数(PP)可以用下列计算得出:
3.标准分
标准分数可以通过线性转换,也可以通过非线性转换得到,由此可将标准分数分为两类。
(1)线性转换的标准分数
当原始数据呈正态分布(normal distribution)时,可以通过线性转换的到标准分数。
其中,X为任一原始分数,X为样本平均数,SD为样本标准差。
Z’=A+Bz
这里Z’为由Z导出的导出分数,A、B为根据需要指定的常数。
加上一个常数是为了去掉负值,乘以一个常数是为了使单位变小从而去掉小数点。
(2)非线性转换的标准分数——正“太”化的标准分(嘿嘿)
当原始分数不是正态分布时,也可以使之正态化(normalized standard score),这一转换过程就是非线性的。
正态化过程主要是将原始分数转化为百分等级,然后使用正态分布表,将对应的百分等级直接看成是正态分布曲线下的面积值,找出所对应的Z值,这种方式所得到的分数叫做正态化的标准分数。
下图即为负偏态分布(negative skewness distribution)转化为正态分布的示意图。
(3)标准分的变式
由于Z分数常常带有小数和出现负值,因此产生了多种将Z分数做线性变换,使负号与小数消失,全部变为正数的转换方法。
T分数(1939年,美国的麦柯尔提出):
T =10Z + 50(μ=50,σ=10)
美国大学入学考试分数(如SAT)
CEEB =100Z + 500(μ=500,σ=100)
美国的韦克斯勒智力测验的智商
分量表智商:DIQ = 3Z + 10(μ=10,σ=3)
总量表智商:DIQ = 15Z + 100(μ=100,σ=15)
美国斯坦福-比奈智力测验智商:DIQ = 16Z + 100 *智商及其意义
若心理年龄高于其生理年龄,则智力较一般儿童高,若心理年龄低于其生理年龄,则智力较一般儿童低。
但在使用中发现,单纯用心理年龄来表示智力高低的方法缺乏不同年龄儿童间的可比性。
1.比率智商
比率智商(IQ)被定义为心理年龄(MA)与真实年龄(CA)之比。
因为心理年龄与实足年龄并不同步增长,所以比率智商并不适合于年龄较大的被试。
2.离差智商
心理学家韦克斯勒提出了离差智商的概念,他将离差智商的平均数定为100,标准差定为15。
所以离差智商是建立在统计学的基础上,它表示的是个体智力在年龄组中所处的位置。
因而是表示智力高低的一种理想指标。
以上标准分的变式既可以使用正态分布下的Z值进行线性转换得到,也可以使用非正态分布下的正态化的Z值进行线性转换得到。
4.标准九分(stanine scale)
标准九分是另一较知名的标准分数系统,其量表是个9级的分数量表。
它是以5为平均数,以2为标准差的一个分数量表。
常态化的标准分数还有标准十分(stanine scale)和标准二十分(sten scale)。
前者平均数为5,标准差为1.5;后者平均数为10,标准差为3。