高中数学 1.2流程图同步练习 苏教版必修3

第1章算法初步1．2013 年全运会在沈阳举行，运动员 A 报名参赛100米短跑并经过初赛、半决赛、决赛最后获取了银牌．问题 1：请简要写出该运动员参赛并获银牌的过程．提示：报名参赛→初赛→半决赛→决赛．问题 2：上述参胜过程有何特色？提示：参胜过程是明确的．问题 3：倘若你家住南京，想去沈阳观看 A 的决赛，你怎样设计你的旅途？提示：第一预定定票，而后选择适合的交通工具到沈阳，准时出席，检票入场，进入竞赛场所，观看竞赛．x ＋＝2，①2．给出方程组yx－ y＝1，②问题 1：利用代入法求解此方程组．提示：由①得y＝2－x，③把③代入②得x－(2－x)＝1，3即 x＝2.④把④代入③得1y＝.23x＝2，获取方程组的解1y＝2.问题 2：利用消元法求解此方程组．3提示：①＋②得x＝2.③3 1x ＝ 2，将③代入①得y ＝ ，得方程组的解2y ＝ 1.问题 3：从问题 1、 2 能够看出，解决一类问题的方法独一吗？提示：不独一．1．算法的观点对一类问题的机械的、一致的求解方法称为算法．2．算法的特色(1) 算法是指用一系列运算规则能在有限步骤内求解某类问题，此中的每条规则一定是明确立义的、可行的．(2) 算法从初始步骤开始，每一个步骤只好有一个确立的后继步骤，进而构成一个步骤序列，序列的停止表示问题获取解答或指出问题没有解答．1．算法的基本思想就是探究解决问题的一般性方法，并将解决问题的步骤用详细化、程序化的语言加以表述．2．算法是机械的，有时要进行大批重复计算，只需循规蹈矩地去做，总能算出结果，往常把算法过程称为“数学机械化”，其最大长处是能够让计算机来达成．3．求解某一个问题的算法不必定只有独一的一个，可能有不一样的算法．[ 例 1] 以下对于算法的说法：①求解某一类问题的算法是独一的②算法一定在有限步操作后停止③算法的每一步操作一定是明确的，不可以存在歧义④算法履行后必定能产生确立的结果此中，不正确的有 ________．[ 思路点拨 ] 利用算法特色对各个表述逐个判断，而后解答．高中数学苏教版必修三教学案：第1章1.2流程图含答案[ 精解析 ]由算法的不独一性，知①不正确；由算法的有性，知②正确；由算法确实定性，知③和④正确．[答案]①[一点通]1．个型的，正确理解算法的观点及其特色是解决此的关．2．注意算法的特色：有限性、确立性、可行性．1．以下句表达中是算法的有________．①从南到巴黎能够先乘火到北京，再坐机到达1②利用公式S＝2ah 算底1，高2的三角形的面1③2x>2x＋4④求 M(1,2)与 N(－3，－5)两点的方程，可先求MN的斜率，再利用点斜式方程求得分析：算法是解决的步与程，个其实不限于数学．①②④都表达了一种算法．答案：①②④2．算以下各式中的S ，能算法求解的是________．①S＝1＋2＋3＋⋯＋100②S＝1＋2＋3＋⋯＋100＋⋯③S＝1＋2＋3＋⋯＋ n( n≥1且 n∈N)分析：算法的要求步是可行的，而且在有限步以内能达成任．故①、③可算法求解．答案：①③[ 例 2]已知直l 1：3x－y＋12＝0和 l 2：3x＋2y－6＝0，求 l 1，l 2， y 成的三角形的面．写出解决本的一个算法．[ 思路点 ]先求出l1，l2的交点坐，再求l 1， l 2与 y 的交点的坐，即获取三角形的底；最后求三角形的高，依据面公式求面．3x－y＋ 12＝ 0，[ 精解析 ]第一步解方程得l1，l2的交点P(－3x＋ 2y－ 6＝ 02,6) ；第二步在方程 3x－y＋ 12＝ 0 中令x＝0 得y＝ 12，进而获取A (0,12) ；第三步在方程 3 x ＋2 －6＝0 中令x ＝0 得 y ＝ 3，获取 (0,3) ；yB第四步 求出△ ABP 底边 AB 的长 | AB | ＝12－ 3＝ 9；第五步求出△ ABP 的底边 AB 上的高 h ＝2；1第六步 代入三角形的面积公式计算S ＝2| AB | · h ；第七步 输出结果．[一点通]设计一个详细问题的算法，往常按以下步骤：(1) 仔细剖析问题，找出解决本题的一般数学方法； (2) 借助相关变量或参数对算法加以表述； (3) 将解决问题的过程区分为若干步骤；(4) 用精练的语言将这个步骤表示出来．3．写出求两底半径分别为1 和 4，高也为 4 的圆台的侧面积、表面积 及体积的算法．解：算法步骤以下：第一步 取 r1＝1， 2＝4， ＝4；rh第二步第三步第四步第五步计算 l ＝r 2－ r 12＋ h 2；22＝π(r ＋ r ) l ；计算 S ＝π r，S ＝π r ； S1122侧1 2计算 S 表＝S ＋S ＋S；12侧1计算 V ＝ 3( S 1＋ S 1S 2＋ S 2 ) h .4．已知球的表面积为 16π，求球的体积．写出解决该问题的两个算法．解：算法 1：第一步 S ＝16π；第二步计算 ＝S ( 因为 ＝4π 2) ；R4πS R第三步 计算 V ＝34πR 3 ；第四步 输出运算结果 V .算法 2：第一步＝16π；S计算 V ＝4S3第二步3π(4π )；第三步输出运算结果V.[例3](12分 ) 某居民区的物业部门每个月向居民收取卫生费，计算方法是：3人或 3人以下的住宅，每个月收取 5 元；超出 3 人的住户，每高出 1 人加收 1.2元．设计一个算法，依据输入的人数，计算应收取的卫生费．[ 精解详析 ]设某户有 x 人，依据题意，应收取的卫生费y 是 x 的分段函数，即 y＝5，≤3，x(4 分)1.2 x＋ 1.4 ，x>3.算法以下：第一步输入人数 x；(6 分)第二步假如 x≤3，则 y＝5，假如 x>3，则 y＝1.2 x＋1.4；(10 分)第三步输出应收卫生费 y.(12分)[一点通]对于此类算法设计应用问题，应该第一成立过程模型，依据模型，达成算法．注意每步设计时要用简炼的语言表述．5．以下算法：第一步输入 x 的值；第二步若 x≥0成立，则 y＝2x，不然履行第三步；第三步y＝log2(－ x)；第四步输出 y 的值．若输出结果 y 的值为4，则输入的x的值为 ________．分析：算法履行的功能是给定x，2x，x≥0，求分段函数 y＝－ x 对应的函数值．log 2， x<0由 y＝4知2x＝4或log2(－ x)＝4.∴x＝2或－16.答案： 2 或－ 166．已知直角三角形的两条直角边分别为a， b，设计一个求该三角形周长的算法．解：算法以下：第一步计算斜边 c＝a2＋ b2；第二步计算周长 l ＝a＋ b＋ c；第三步输出 l .1．算法的特色：有限性、确立性、逻辑性、不独一性、广泛性．2．在详细设计算法时，要明确以下要求：(1)算法设计是一类问题的一般解法的抽象与归纳，它要借助一般问题的解决方法，又要包括这种问题的全部可能情况．设计算法时常常要把问题的解法区分为若干个可履行的步骤，有些步骤是重复履行的，但最后却一定在有限个步骤以内达成．(2)借助相关的变量或参数对算法加以表述．(3)要使算法尽量简单，步骤尽量少．课下能力提高( 一 )一、填空题1．写出解方程2x＋ 3＝ 0 的一个算法过程．第一步 __________________________________________________________________ ；第二步 __________________________________________________________________ ．答案：第一步将常数项 3 移到方程右侧得2x＝－ 3；3第二步在方程两边同时除以2，得x＝－2.2．已知一个学生的语文成绩为89，数学成绩为96，外语成绩为99. 求他的总分和均匀分的一个算法为：第一步令 A＝89， B＝96， C＝99；第二步计算总分 S＝________；第三步计算均匀分M＝________；第四步输出 S和 M.分析：总分S 为三个成绩数之和，A＋B＋C S均匀数 M＝3＝3.答案： A＋ B＋ C S 33．给出以下算法：第一步输入 x 的值；第二步当x >4 时，计算y＝＋ 2；不然履行下一步；x第三步计算 y＝4－x；第四步输出 y.当输入 x＝0时，输出 y＝__________.分析：因为x＝0>4不可立，故y＝4－x＝ 2.答案： 24．已知点P0( x0， y0)和直线 l ： Ax＋By＋ C＝0，求点到直线距离的一个算法有以下几步：①输入点的坐标x0， y0；②计算 z1＝ Ax0＋By0＋ C；③计算 z2＝ A2＋ B2；④输入直线方程的系数A， B和常数 C；⑤计算＝ | z1|；z2⑥输出 d 的值．其正确的次序为 ________．分析：利用点到直线的距离公式：| 0＋0＋|Ax By Cd＝A2＋ B2.答案：①④②③⑤⑥5．已知数字序列： 2,5,7,8,15,32,18,12,52,8.写出从该序列搜寻18 的一个算法．第一步输入实数 a.第二步__________________________________________________________________.第三步输出 a＝18.分析：从序列数字中搜寻18，一定挨次输入各数字才能够找到．答案：若 a＝18，则履行第三步，不然返回第一步二、解答题6．写出求a， b， c 中最小值的算法．解：算法以下：第一步比较a ，b的大小，当>时，令“最小值”为b；不然，令“最小值”为a；a b第二步比较第一步中的“最小值”与 c 的大小，当“最小值”大于 c 时，令“最小值”为c；不然，“最小值”不变；第三步“最小值”就是a， b， c 中的最小值，输出“最小值”．7．某铁路部门规定甲、乙两地之间游客托运转李的花费为c＝0.53 ω，ω≤50，50×0.53 ＋ω－ 50×0.85 ，ω >50.此中ω(单位：kg)为行李的重量，怎样设计计算花费c(单位：元)的算法．解：算法步骤以下：第一步输入行李的重量ω；第二步假如ω≤50，那么c＝0.53ω ；假如ω>50，那么c＝50×0.53＋(ω－50)×0.85；第三步输出运费 c.8．下边给出一个问题的算法：第一步输入 a；第二步若 a≥4，则履行第三步，不然履行第四步；第三步输出 2a－ 1；第四步输出 a2－2a＋3.问题： (1) 这个算法解决的是什么问题？(2)当输入a 等于多少时，输出的值最小？解： (1) 这个算法解决的问题是求分段函数2x－ 1，x≥4，f ( x)＝x2－2x＋3，x<4的函数值问题．(2)当 x≥4时， f ( x)＝2x－1≥7，当 x<4时， f ( x)＝ x2－2x＋3＝( x－1)2＋2≥2.∴当 x＝1时， f ( x)min＝2.即当输入 a 的值为1时，输出的值最小．。

图3图4图2图1a←2b←5c←b+aa←c+4PRINT a,b第一章算法初步1.2流程图1.2.1顺序结构一、选择题:1.下面程序框图中具有计算功能的是 ( )A. B. C. D.2.下面说法正确的是 ( )A.程序框图是由矩形框和线段组成的B. 带箭头的流程线上算法的运行是可逆的C.终端框表示一个算法的结束D.输入输出框表示一个算法的输入和输出信息3. 1+2+3+4+…+________>2004，在横线上写出最小的正整数为( )A. 61B. 62C. 63D. 644.下列程序框图中只允许一流入线的是 ( )A.起始框B.处理框C.终止框D.输入框5.读图1的程序，输出的结果是 ( )A. 2 5B. 4 5C. 11 5D. 7 56.图2中所示的是一个算法的流程图，已知31=a，输出的b=7,则2a的值是( )A．11 B．17 C．0.5 D．12二、填空题:7.流程图，则输出的结果是 .8.画一个程序框图计算1000234÷, 如下图4所示,则①应填.9.某学生五门功课成绩为80，95，78，87，65.如下图5为一个算法流程图,该算法流程图的意义为___________________.其算法为: S1 ; S2 ; S3 ; S4 ; S5 ; S6 ; S7 .10.完成下面的表格:二、解答题:的算法流程图.11.试画一个计算630%12.画出由梯形两底a、b和高h，求梯形面积的算法流程图.13. 确定线段AB 的5等分点,是指在线段AB 上确定一点M ,使得AM =51AB .画出这个算法的流程图.14. 已知直线l 1：Ax +By +C 1=0和直线l 2：Ax +By +C 2=0，写出直线l 1与直线l 2的距离d 的算法流程图.15. 已知点P （x 0，y 0）和直线l ：Ax +By +C =0，求点P 到直线l 的距离.用流程图表示这种算法.拓展创新——练能力16. 一个人带一保狼、一只羊和一筐青菜准备过河. 但因船小过河时每次只能带一样东西,然而人不在时,狼会把羊吃掉,羊也会把菜吃掉. 请你设计一个程序,并画出程序框图,使人能将所有东西全部带到对岸.17.“鸡兔同笼“是我国隋朝时期的数学著作《孙子算经》中的一个有趣而具有深远影响的题目：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何。

1.2 流程图1、对任意非零实数,a b ，若a b ⊗的运算原理如图所示，则221(log 8)()2-⊗（ ）A. 1B. 2C.-1D. 4 2、上面框图表示的程序所输出的结果是( )A.11B.12C.132D.13203、某程序框图如下图所示，该程序运行后输出的k 的值是（ ）A.4B.5C.6D.74、如图所示，程序框图(算法流程图)的输出结果是( )A．34 B．55 C．78 D．89 5、按照下图的程序框图计算,若开始输入的值为3,则最后输出的结果是( )A.6B.21C.231D.50506、如图，程序框图输出的结果为（）A.19 10B.910C.1011D.21117、执行如图所示的程序框图，输出的s值为（）A. -3B.-12C. 13D. 28、执行如图所示的程序框图，输出S的值为（）A.7B.14C.30D.419、执行如图所示的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为（）A.5B.4C.3D.210、我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n ( )A．4 B．5 C．2 D．311、执行如图所示的程序框图，输出的s值为．12、执行如图所示的程序框图，输出的s值为．13、如图是一个算法流程图,则输出的S的值是 .14、执行如图所示的程序框图，若输入的240,176==，则输出的a值为______________.a b15、已知如图所示的程序框图.(1)当输入的x 为2，-1时，分别计算输出的y 值，并写出输出值y 关于输入值x 的函数关系式；(2)当输出的结果为4时，求输入的x 的值.答案以及解析1答案及解析：答案：C解析：2答案及解析：答案：D解析：i 12=时,11212S =⨯=;i 11=时,1211132S =⨯=;i 10=时,132101320S =⨯=;i 9=时,i 10<,故输出1320S =.3答案及解析：答案：A解析：4答案及解析：答案：B解析：5答案及解析：答案：C解析：6答案及解析：答案：A解析：7答案及解析：答案：D解析：8答案及解析：答案：C解析：9答案及解析：答案：D解析：当输入的正整数N 是所给选项中最小的正整数2时,1t = ,100M = ,0S = ,则第一次循环,1000100100,10,210S M t =+==-=-=；第二次循环,101001090,1,310S M =-==-== ,此时2t ≤不成立,输出9091S =<.故选D10答案及解析：答案：A解析：11答案及解析： 答案：56解析：模拟程序的运行过程，第一次运行：1k =时，()1111111122s =+-⨯=-=+， 第二次运行：2k =时，111151212236s =+⨯=+=+， 第三次运行：此时3k =满足，退出循环，输出56s =， 故答案为56．12答案及解析： 答案：56 解析：模拟程序的运行过程，第一次运行：1k =时，()1111111122s =+-⨯=-=+， 第二次运行：2k =时，111151212236s =+⨯=+=+， 第三次运行：此时3k =满足，退出循环，输出56s =， 故答案为56．13答案及解析：答案：5 解析：执行算法流程图，11,2x S ==，不满足条件；32,2x S ==，不满足条件；3,3x S ==，不满足条件；45x S ==，，满足条件，结束循环，故输出的S 的值是5.14答案及解析：答案：16解析：15答案及解析：答案：(1)当输入的x 为2时，2log 21y ==，当输入的x 为-1时，1122y -⎛⎫== ⎪⎝⎭. 输出值y 关于输入值x 的函数关系式为2log ,01,02x x x y x >⎧⎪=⎨⎛⎫≤⎪⎪⎝⎭⎩ (2)当0x >时，2log 4y x ==，解得16x =；当0x ≤时，142xy ⎛⎫== ⎪⎝⎭，解得2x =-. 综上，当输出的结果为4时，输入的x 的值为16或-2. 解析：。

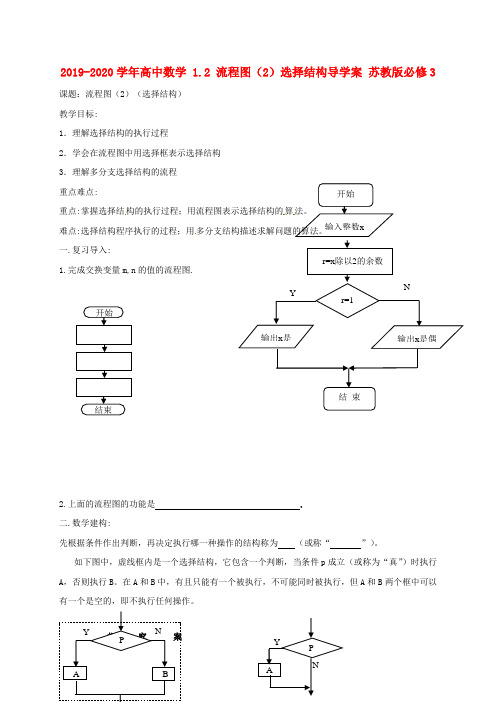
结束开始2019-2020学年高中数学 1.2 流程图（2）选择结构导学案 苏教版必修3课题：流程图（2）（选择结构） 教学目标:1．理解选择结构的执行过程2．学会在流程图中用选择框表示选择结构 3．理解多分支选择结构的流程 重点难点:重点:掌握选择结构的执行过程；用流程图表示选择结构的算法。

难点:选择结构程序执行的过程；用多分支结构描述求解问题的算法。

一.复习导入:1.完成交换变量m,n 的值的流程图.2.上面的流程图的功能是 . 二.数学建构:先根据条件作出判断，再决定执行哪一种操作的结构称为 （或称“ ”）。

如下图中，虚线框内是一个选择结构，它包含一个判断，当条件p 成立（或称为“真”）时执行A ，否则执行B 。

在A 和B 中，有且只能有一个被执行，不可能同时被执行，但A 和B 两个框中可以有一个是空的，即不执行任何操作。

开始输入整数x r=1 输出x 是输出x 是偶结 束YNr=x 除以2的余数Y P AN探究一：1. 下图的算法流程图是为 问题而设计的.（1） （2）2.如果考生的成绩大于或等于60分，则输出“及格”，否则输出“不及格”，完成上的流程图. 探究二：1、下面的流程图当输入值分别是2,8,3时，输出的值为开始 输入成绩xYN及格结束开始 输入实数aa ≥0Y N输出输出“不存在” 结束a（1）（2）（3）2、上面是一个算法的流程图，当输入的值为3时,输出的结果为3、完成下面的流程图：.完成下面的解一元二次方程ax2+bx+c=0的流程图.。

【学案导学设计】2015—2016学年高中数学 1、2习题课课时作业苏教版必修3课时目标1、理解并掌握画流程图的规则、2、在具体问题的解决过程中,理解流程图的三种基本逻辑结构、3、能正确选择并运用三种逻辑结构框图表示具体问题的算法、1、下列关于流程图的描述①对于一个算法来说流程图就是唯一的；②任何一个流程图都必须有起止框;③流程图只有一个入口,也只有一个出口;④输出框一定要在终止框前、其中正确的有________个、2、早上从起床到出门需要洗脸刷牙(5 min)、刷水壶（2 min）、烧水(8 min）、泡面（3 min)、吃饭(10 min)、听广播（8 min）几个步骤、从下列选项中选出最好的一种流程________、①1、洗脸刷牙、2、刷水壶、3、烧水、4、泡面、5、吃饭、6、听广播②1、刷水壶、2、烧水同时洗脸刷牙、3、泡面、4、吃饭、5、听广播③1、刷水壶、2、烧水同时洗脸刷牙、3、泡面、4、吃饭同时听广播④1、吃饭同时听广播、2、泡面、3、烧水同时洗脸刷牙、4、刷水壶3、如图就是一个算法的流程图，该算法所输出的结果就是________、4、阅读下边的流程图，若输出s的值为－7,则判断框内可填写________、5、求边长为3，4，5的直角三角形的内切圆半径的算法为: S1 __________________；S2 r ←a ＋b －c2；S3 输出r 、6、根据下面的流程图操作,使得当成绩不低于60分时，输出“及格”,当成绩低于60分时,输出“不及格”,则框1中填________，框2中填________、一、填空题1、一个完整的流程图至少包含________框、2、下列流程图表示的算法就是________、3、完成求1×2×3×…×10的算法、S1 I←1;S2 k←2;S3 I←I×k;S4 k←________;S5 ______________S6 输出I、4、阅读下边的流程图，运行相应的程序,则输出的i值为________、5、如图给出的就是计算错误!＋错误!＋错误!＋…＋错误!的值的一个流程图,其中判断框内应填入的条件就是________、6、读下面流程图则循环体执行的次数为________次、7、直到型循环结构框图为________、8、已知下列框图，若a＝5,则输出b＝________、9、执行如图所示的流程图，若输入x＝4,则输出y的值为________、二、解答题10、已知点P0（x0，y0)与直线l：Ax＋By＋C＝0，写出求点P0到直线l的距离d的算法并画出流程图、11、画出求满足12＋22＋32＋…＋i2>106的最小正整数n的流程图、能力提升12、一队士兵来到一条有鳄鱼的深河的左岸、只有一条小船与两个小孩,这条船只能承载两个小孩或一个士兵、试设计一个算法，将这队士兵渡到对岸，并将这个算法用流程图表示、13、某工厂2010年生产轿车200万辆,技术革新后预计每年的产量比上一年增加5%，问最早哪一年生产的轿车超过300万辆？试设计算法并画出相应的流程图、1、流程图就是用规定的图形、流程线及文字说明表示算法的图形,因此首要任务应就是会画基本的流程图并熟知它们的功能、2、画流程图必须遵守一些共同的规则：（1)使用框图的符号要标准、(2)框图一般按从上到下、从左到右的顺序画、（3)除了判断框外,大多数框图符号只有一个进入点与一个退出点,判断框就是唯一具有超过一个退出点的框图符号、（4)判断框有两种:一种就是“Y"与“N”两个分支的判断，而且有且仅有两个结果；另一种就是多分支判断,有几种不同的结果,这种判断框中学阶段很少用到、（5)在图形符号内描述的语言要简练清楚、答案双基演练1、2解析②、③正确,对于一个算法来说，流程图不唯一，与设计有关，故①错、输入输出的位置，不一定在开始与结束处，故④错、2、③解析①中洗脸刷牙可以在烧水的过程中进行，听广播可以与吃饭同时进行；④中吃饭要在刷水壶、烧水、泡面之后、3、错误!解析运行第一次的结果为n＝0＋错误!＝错误!;第二次n＝错误!＋错误!＝错误!;第三次n＝错误!＋错误!＝错误!、此时i＝4程序终止,即输出n＝错误!、4、i<6(或i〈7，i≤5，i≤6)解析i＝1,s＝2；s＝2－1＝1，i＝1＋2＝3;s＝1－3＝－2，i＝3＋2＝5;s＝－2－5＝－7,i＝5＋2＝7、因输出s的值为－7，循环终止，故判断框内应填“i<6”，或“i〈7”或“i≤5"或“i≤6"、5、a←3，b←4,c←56、Y N解析由x≥60与及格对应知错误!处填Y,则错误!处填N、作业设计1、起止框与输入、输出解析一个完整的流程图至少需包括起止框与输入、输出框、2、求三数中的最大值解析根据流程图可知,此图应表示求三个数中的最大数、3、k＋1 若k〉10,那么转S6，否则转S34、4解析 S＝0→i＝1→a＝2→S＝2→i＝2→a＝8→S＝10→i＝3→a＝24→S＝34→i＝4→输出i＝4、5、i≥51（或i〉50)解析i＝1时，S＝0＋错误!＝错误!,i＝2时,S＝错误!＋错误!,…,i＝50时，S＝错误!＋错误!＋错误!＋…＋错误!，当i＝51时结束程序、6、49解析∵i＝i＋2，∴当2＋2n≥100时循环结束此时n＝49、7、②8、26解析因a＝5，所以5>5不成立,判断框执行“N”，即b＝52＋1＝26、9、－错误!解析当输入x＝4时，计算y＝错误!x－1,得y＝1、不满足｜y－x|〈1、于就是得x＝1,此时y＝错误!－1＝－错误!，不满足｜－错误!－1|<1，此时x＝－错误!，得y＝－错误!、这样｜y－x|＝|－错误!＋错误!|＝错误!<1,执行“Y",所以输出的就是－错误!、10、解(1）用数学语言来描述算法：S1 输入点的坐标x0,y0,输入直线方程的系数即常数A,B,C；S2 z1←Ax0＋By0＋C；S3 z2←A2＋B2;S4 d←错误!;S5 输出d、(2）用流程图来描述算法,如图：11、解流程图如下:12、解第1步，两个儿童将船划到右岸;第2步,她们中一个上岸,另一个划回来;第3步,儿童上岸,一个士兵划过去;第4步,士兵上岸，让儿童划回来；第5步,如果左岸没有士兵,那么结束，否则转第1步、流程图如图所示、2016苏教版必修3高中数学1.2《流程图》word课时作业13、解算法如下：S1 n←2 010；S2 a←200；S3 T←0、05a；S4 a←a＋T;S5 n←n＋1;S6 若a〉300，输出n、否则转S3、流程图：。

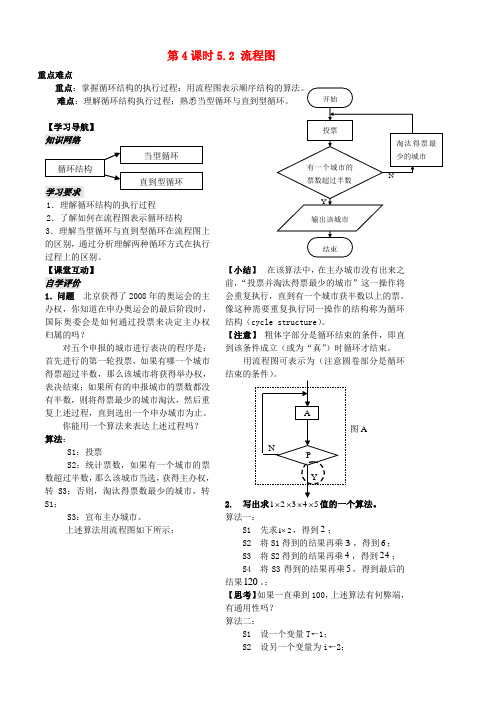
第4课时5.2 流程图重点难点重点难点【学习导航】1．理解循环结构的执行过程2．了解如何在流程图表示循环结构3．理解当型循环与直到型循环在流程图上的区别，通过分析理解两种循环方式在执行过程上的区别。

【课堂互动】自学评价1．问题 北京获得了2008年的奥运会的主办权，你知道在申办奥运会的最后阶段时，国际奥委会是如何通过投票来决定主办权归属的吗？对五个申报的城市进行表决的程序是：首先进行的第一轮投票，如果有哪一个城市得票超过半数，那么该城市将获得举办权，表决结束；如果所有的申报城市的票数都没有半数，则将得票最少的城市淘汰，然后重复上述过程，直到选出一个申办城市为止。

你能用一个算法来表达上述过程吗？算法：S1：投票S2：统计票数，如果有一个城市的票数超过半数，那么该城市当选，获得主办权，转S3；否则，淘汰得票数最少的城市，转S1；S3：宣布主办城市。

上述算法用流程图如下所示：【小结】 在该算法中，在主办城市没有出来之前，“投票并淘汰得票最少的城市”这一操作将会重复执行，直到有一个城市获半数以上的票。

像这种需要重复执行同一操作的结构称为循环结构（cycle structure ）。

【注意】 粗体字部分是循环结束的条件，即直到该条件成立（或为“真”）时循环才结束。

用流程图可表示为（注意圆卷部分是循环 2. 写出求12345⨯⨯⨯⨯值的一个算法。

算法一： S1 先求12⨯，得到2； S2 将S1得到的结果再乘3，得到6； S3 将S2得到的结果再乘4，得到24； S4 将S3得到的结果再乘5，得到最后的结果120。

； 【思考】如果一直乘到100，上述算法有何弊端，有通用性吗？ 算法二： S1 设一个变量T ←1； S2 设另一个变量为i ←2；图AS3 T ←T ×i { 将T ×i 的结果仍放在变量T 中 }；S4 i ←i+1 {i 的值增加1}；S5 如果i 不大于5，转S3，否则输出T ，算法结束。

1.2.1 流程图
备课资料
备用习题
1.写出求某学生的语文、数学、英语、物理、化学五门成绩的平均分的一个算法，并
根据这个算法写出流程图.
解：算法：
图14
S1 输入语文、数学、英语、物理、化学五门成绩a，b，c，d，e；
S2 x=；
S3 输出x.
流程图如图14所示：
2.设计计算上底为3，下底为7，高为6的梯形的面积的算法，并画出流程图.
解：算法：
S1 令a←3；
S2 令b←7；
S3 令h←6；
S4 计算S=；
S5 输出S.
流程图如图15所示：
图15
3.交换三个数x、y、z的值，使得x的值赋给y，y的值赋给z，x的值为原始的z的值.设计出解决这个问题的一个算法，并画出流程图.
解：算法：
S1 输入x，y，z；S2 t←z；
S3 z←y；
S4 y←x；
S5 x←t；
S6 输出x，y，z. 流程图如图16所示：
图16。

第1章 算 法 初 步1．2013年全运会在沈阳举行，运动员A 报名参赛100米短跑并通过预赛、半决赛、决赛最后获得了银牌．问题1：请简要写出该运动员参赛并获银牌的过程． 提示：报名参赛→预赛→半决赛→决赛． 问题2：上述参赛过程有何特征？ 提示：参赛过程是明确的．问题3：假若你家住南京，想去沈阳观看A 的决赛，你如何设计你的旅程？提示：首先预约定票，然后选择合适的交通工具到沈阳，按时到场，检票入场，进入比赛场地，观看比赛．2．给出方程组⎩⎪⎨⎪⎧x ＋y ＝2， ①x －y ＝1， ②问题1：利用代入法求解此方程组． 提示：由①得y ＝2－x ，③把③代入②得x －(2－x )＝1， 即x ＝32.④把④代入③得y ＝12.得到方程组的解⎩⎨⎧x ＝32，y ＝12.问题2：利用消元法求解此方程组． 提示：①＋②得x ＝32.③将③代入①得y＝12，得方程组的解⎩⎨⎧x＝32，y＝12.问题3：从问题1、2可以看出，解决一类问题的方法唯一吗？提示：不唯一．1．算法的概念对一类问题的机械的、统一的求解方法称为算法．2．算法的特征(1)算法是指用一系列运算规则能在有限步骤内求解某类问题，其中的每条规则必须是明确定义的、可行的．(2)算法从初始步骤开始，每一个步骤只能有一个确定的后继步骤，从而组成一个步骤序列，序列的终止表示问题得到解答或指出问题没有解答．1．算法的基本思想就是探求解决问题的一般性方法，并将解决问题的步骤用具体化、程序化的语言加以表述．2．算法是机械的，有时要进行大量重复计算，只要按部就班地去做，总能算出结果，通常把算法过程称为“数学机械化”，其最大优点是可以让计算机来完成．3．求解某一个问题的算法不一定只有唯一的一个，可能有不同的算法．[例1]下列关于算法的说法：①求解某一类问题的算法是唯一的②算法必须在有限步操作后停止③算法的每一步操作必须是明确的，不能存在歧义④算法执行后一定能产生确定的结果其中，不正确的有________．[思路点拨]利用算法特征对各个表述逐一判断，然后解答．[精解详析] 由算法的不唯一性，知①不正确； 由算法的有穷性，知②正确； 由算法的确定性，知③和④正确． [答案] ① [一点通]1．针对这个类型的问题，正确理解算法的概念及其特点是解决此类问题的关键． 2．注意算法的特征：有限性、确定性、可行性．1．下列语句表达中是算法的有________．①从济南到巴黎可以先乘火车到北京，再坐飞机抵达 ②利用公式S ＝12ah 计算底为1，高为2的三角形的面积③12x >2x ＋4 ④求M (1,2)与N (－3，－5)两点连线的方程，可先求MN 的斜率，再利用点斜式方程求得解析：算法是解决问题的步骤与过程，这个问题并不仅仅限于数学问题．①②④都表达了一种算法．答案：①②④2．计算下列各式中的S 值，能设计算法求解的是________． ①S ＝1＋2＋3＋…＋100 ②S ＝1＋2＋3＋…＋100＋… ③S ＝1＋2＋3＋…＋n (n ≥1且n ∈N)解析：算法的设计要求步骤是可行的，并且在有限步之内能完成任务．故①、③可设计算法求解．答案：①③[例2] 已知直线l 1：3x －y ＋12＝0和l 2：3x ＋2y －6＝0，求l 1，l 2，y 轴围成的三角形的面积．写出解决本题的一个算法．[思路点拨] 先求出l 1，l 2的交点坐标，再求l 1，l 2与y 轴的交点的纵坐标，即得到三角形的底；最后求三角形的高，根据面积公式求面积．[精解详析] 第一步 解方程组⎩⎪⎨⎪⎧3x －y ＋12＝0，3x ＋2y －6＝0得l 1，l 2的交点P (－2,6)；第二步 在方程3x －y ＋12＝0中令x ＝0得y ＝12，从而得到A (0,12)；第三步 在方程3x ＋2y －6＝0中令x ＝0得y ＝3，得到B (0,3)； 第四步 求出△ABP 底边AB 的长|AB |＝12－3＝9； 第五步 求出△ABP 的底边AB 上的高h ＝2； 第六步 代入三角形的面积公式计算S ＝12|AB |·h ；第七步 输出结果． [一点通]设计一个具体问题的算法，通常按以下步骤： (1)认真分析问题，找出解决此题的一般数学方法； (2)借助有关变量或参数对算法加以表述； (3)将解决问题的过程划分为若干步骤； (4)用简练的语言将这个步骤表示出来．3．写出求两底半径分别为1和4，高也为4的圆台的侧面积、表面积及体积的算法．解：算法步骤如下：第一步 取r 1＝1，r 2＝4，h ＝4； 第二步 计算l ＝(r 2－r 1)2＋h 2；第三步 计算S 1＝πr 21，S 2＝πr 22；S 侧＝π(r 1＋r 2)l ；第四步 计算S 表＝S 1＋S 2＋S 侧； 第五步 计算V ＝13(S 1＋S 1S 2＋S 2)h .4．已知球的表面积为16π，求球的体积．写出解决该问题的两个算法． 解：算法1：第一步 S ＝16π； 第二步 计算R ＝S4π(由于S ＝4πR 2)； 第三步 计算V ＝43πR 3；第四步 输出运算结果V . 算法2：第一步 S ＝16π； 第二步 计算V ＝43π(S 4π)3； 第三步 输出运算结果V .[例3] (12分)某居民区的物业部门每月向居民收取卫生费，计算方法是：3人或3人以下的住房，每月收取5元；超过3人的住户，每超出1人加收1.2元．设计一个算法，根据输入的人数，计算应收取的卫生费．[精解详析] 设某户有x 人，根据题意，应收取的卫生费y 是x 的分段函数，即y ＝⎩⎪⎨⎪⎧5， x ≤3，1.2x ＋1.4，x >3. (4分)算法如下：第一步 输入人数x ；(6分)第二步 如果x ≤3，则y ＝5， 如果x >3，则y ＝1.2x ＋1.4； (10分) 第三步 输出应收卫生费y .(12分)[一点通]对于此类算法设计应用问题，应当首先建立过程模型，根据模型，完成算法．注意每步设计时要用简炼的语言表述．5．如下算法： 第一步 输入x 的值；第二步 若x ≥0成立，则y ＝2x ，否则执行第三步； 第三步 y ＝log 2(－x )； 第四步 输出y 的值．若输出结果y 的值为4，则输入的x 的值为________． 解析：算法执行的功能是给定x ，求分段函数y ＝⎩⎪⎨⎪⎧2x ，x ≥0，log 2(－x )，x <0对应的函数值．由y ＝4知2x ＝4或log 2(－x )＝4. ∴x ＝2或－16. 答案：2或－166．已知直角三角形的两条直角边分别为a ，b ，设计一个求该三角形周长的算法． 解：算法如下： 第一步 计算斜边c ＝a 2＋b 2；第二步 计算周长l ＝a ＋b ＋c ； 第三步 输出l .1．算法的特点：有限性、确定性、逻辑性、不唯一性、普遍性． 2．在具体设计算法时，要明确以下要求：(1)算法设计是一类问题的一般解法的抽象与概括，它要借助一般问题的解决方法，又要包含这类问题的所有可能情形．设计算法时往往要把问题的解法划分为若干个可执行的步骤，有些步骤是重复执行的，但最终却必须在有限个步骤之内完成．(2)借助有关的变量或参数对算法加以表述． (3)要使算法尽量简单，步骤尽量少．课下能力提升(一)一、填空题1．写出解方程2x ＋3＝0的一个算法过程．第一步__________________________________________________________________； 第二步__________________________________________________________________．答案：第一步 将常数项3移到方程右边得2x ＝－3； 第二步 在方程两边同时除以2，得x ＝－32.2．已知一个学生的语文成绩为89，数学成绩为96，外语成绩为99.求他的总分和平均分的一个算法为：第一步 令A ＝89，B ＝96，C ＝99； 第二步 计算总分S ＝________； 第三步 计算平均分M ＝________； 第四步 输出S 和M .解析：总分S 为三个成绩数之和， 平均数M ＝A ＋B ＋C 3＝S3.答案：A ＋B ＋C S33．给出下列算法： 第一步 输入x 的值；第二步 当x >4时，计算y ＝x ＋2；否则执行下一步； 第三步 计算y ＝4－x ； 第四步 输出y .当输入x ＝0时，输出y ＝__________. 解析：由于x ＝0>4不成立，故y ＝4－x ＝2.答案：24．已知点P 0(x 0，y 0)和直线l ：Ax ＋By ＋C ＝0，求点到直线距离的一个算法有如下几步： ①输入点的坐标x 0，y 0； ②计算z 1＝Ax 0＋By 0＋C ； ③计算z 2＝A 2＋B 2；④输入直线方程的系数A ，B 和常数C ； ⑤计算d ＝|z 1|z 2； ⑥输出d 的值．其正确的顺序为________． 解析：利用点到直线的距离公式： d ＝|Ax 0＋By 0＋C |A 2＋B2.答案：①④②③⑤⑥5．已知数字序列：2,5,7,8,15,32,18,12,52,8.写出从该序列搜索18的一个算法． 第一步 输入实数a .第二步 __________________________________________________________________. 第三步 输出a ＝18.解析：从序列数字中搜索18，必须依次输入各数字才可以找到． 答案：若a ＝18，则执行第三步，否则返回第一步 二、解答题6．写出求a ，b ，c 中最小值的算法． 解：算法如下：第一步 比较a ，b 的大小，当a >b 时，令“最小值”为b ；否则，令“最小值”为a ； 第二步 比较第一步中的“最小值”与c 的大小，当“最小值”大于c 时，令“最小值”为c ；否则，“最小值”不变；第三步 “最小值”就是a ，b ，c 中的最小值，输出“最小值”． 7．某铁路部门规定甲、乙两地之间旅客托运行李的费用为c ＝⎩⎪⎨⎪⎧0.53ω， ω≤50，50×0.53＋(ω－50)×0.85， ω>50. 其中ω(单位：kg)为行李的重量，如何设计计算费用c (单位：元)的算法． 解：算法步骤如下： 第一步 输入行李的重量ω；第二步 如果ω≤50，那么c ＝0.53ω； 如果ω>50，那么c ＝50×0.53＋(ω－50)×0.85； 第三步 输出运费c .8．下面给出一个问题的算法： 第一步 输入a ；第二步 若a ≥4，则执行第三步，否则执行第四步； 第三步 输出2a －1； 第四步 输出a 2－2a ＋3.问题：(1)这个算法解决的是什么问题？ (2)当输入a 等于多少时，输出的值最小？解：(1)这个算法解决的问题是求分段函数f (x )＝⎩⎪⎨⎪⎧2x －1，x ≥4，x 2－2x ＋3，x <4的函数值问题．(2)当x ≥4时，f (x )＝2x －1≥7，当x <4时，f (x )＝x 2－2x ＋3＝(x －1)2＋2≥2. ∴当x ＝1时，f (x )min ＝2.即当输入a 的值为1时，输出的值最小．。

自主广场我夯基 我达标1．算法的三种基本结构是( )A ．顺序结构、选择结构、循环结构B ．顺序结构、流程结构、循环结构C ．顺序结构、分支结构、流程结构D ．流程结构、分支结构、循环结构思路解析：本题考查算法的三种基本结构.算法常见的基本结构有三种：顺序结构、选择结构和循环结构.★答案★：A2．流程图中表示判断框的是( )A ．矩形框B ．菱形框C ．圆形框D ．椭圆形框思路解析：本题考查流程图中各种框图的形状和功能.解此类题一定要记清各类框图的形状和功能：矩形框表示计算和赋值；平行四边形框表示输入和输出；菱形框表示判断，则此题★答案★应为B.★答案★：B3．图5-17是求解一元二次方程ax 2+bx+c=0（a ≠0）的流程图，请在空缺的地方填上适当的标注.图5-17思路解析：根据解一元二次方程的步骤填空即可.解一元二次方程时首先要求方程的判别式，当判别式小于0时，方程无解，当判别式大于或等于0时方程有两个实根.★答案★：（1）Δ＜0 （2）．a b x 21∆+-←．ab x 22∆+-←（3）输出x 1，x 2 4．图5-18所示的流程图表示了一个什么样的算法？图5-18思路解析：本题考查了选择结构在算法中的应用和功能.由第一个判断框可知，当a为a、b、c中的最小数时输出a的值，否则比较b与c的大小，由第二个判断框可知哪个数小则输出哪个数.★答案★：输入三个数，输出其中最小的一个.5．图5-19所示的流程图是当型循环还是直到型循环？它表示了一个什么样的算法？图5-19思路解析：两种循环结构的区别是：(1)执行情况不一样.当型结构是先判断循环条件，当条件成立时，才执行语句块A，若循环条件一开始就不成立，则语句块A一次也不执行,而直到型结构是先执行语句块A，后判断循环条件，且语句块A至少要执行一次. (2)循环结束条件不一样.当型结构是条件不成立时结束循环，而直到型结构是条件成立时结束循环.且由流程图可以看出，只要n的值不大于100就反复执行sum←sum+n、n←n+1.所以它表示的是求1+2+3+…+100的算法.★答案★：此流程图为先判断后执行，为当型循环,它表示求1+2+3+…+100的值的算法. 6．已知梯形的上底、下底和高分别为5、8、9，写出求梯形的面积的算法，并画出流程图.思路解析：本题考查顺序结构在算法中的应用.由于求梯形的面积只需代入其面积公式S=2)(hba即可.★答案★：算法如下：S1 a←5；S2 b←8；S3 h←9；S4 S←2)(hba；S5 输出S.流程图如下：7．设计算法流程图，输出2 000以内除以3余1的正整数.思路解析：由于1除以3之后余数是1，则1+3除以3余数是1;1+3+3除以3余数也是1，….由于求的是2000以内除以3余1的正整数，则画流程图时应采用选择结构和循环结构.★答案★：流程图如下:8．某学生五门功课成绩为80、95、78、87、65.写出求其平均成绩的算法，并画出流程图.思路解析：本题考查顺序结构在算法中的应用，只要将五个数相加求和之后再除以5即可求得.★答案★：算法如下：S1 S←80；S2 S←S+95；S3 S←S+78；S4 S←S+87；S5 S ←S+65；S6 A←S/5；S7 输出A.流程图如下：9．假设超市购物标价不超过100元时按九折付款，如标价超过100元，则超过部分按七折收费.写出超市收费的算法，并画出流程图.思路解析：本题相当于求分段函数的函数值的问题.设所购物品标价为x 元，超市收费为y 元,则y=⎩⎨⎧-⨯+⨯≤．x x ，)100(7.01009.0 100， x 9.0收费时应先判断标价是否大于100，且应采用选择结构.★答案★:其算法如下：S1 输入标价x ；S2 如果x ≤100，那么y=0.9x ；否则y=0.9×100+0.7×（x －100）；S3 输出标价x 和收费y. 流程图如下：10．写出求1×3×5×7×9×11的值的算法，并画出流程图.思路解析：由题意可知，本题相当于求连续奇数的积的一个算法，则此算法可利用顺序结构.又由于因数的个数比较多，则为了简化算法过程，则可利用选择结构画出其流程图.★答案★：算法如下：S1 p ←1；S2 I ←3；S3 p ←p ×I ；S4 I ←I ＋2；S5 若I ≤11，返回S3；否则，输出p 值，结束.流程图如下：我综合 我发展11．2005年10月27日,由全国人大通过的《中华人民共和国个人所得税法》(第三次修订)规定，公民全月工资、薪金所得不超过1 600元的部分不必纳税，超过1 600元的部分为全月应纳税所得额，此项税款按下表分段累进计算：全月应纳税所得额 税 率 不超过500元的部分 5% 超过500元至2 000元的部分 10% 超过2 000元至5 000元的部分15%试写出工资x （x ≤5 000元）与税收y 的函数关系式，给出计算应纳税所得额的算法及流程图.思路解析：研究这个表提供的信息，可以发现，如果以一个人的工资、薪金所得为自变量x ，那么应纳税款y ＝f （x ）就是x 的一个分段函数.y=⎪⎪⎩⎪⎪⎨⎧≤<+≤<-+≤<≤< 000． 5x 600 3 600)，3-0.15(x 175 600， 3x 2100 )2100(1.025 100， 2x 600 1 1600)，-0.05(x 600， 1x 0 0，x ，而表示分段函数求值的算法的流程图一般用选择结构.★答案★：y=⎪⎪⎩⎪⎪⎨⎧≤<+≤<-+≤<≤< 000． 5x 600 3 600)，3-0.15(x 175 600， 3x 2100 )2100(1.025 100， 2x 600 1 1600)，-0.05(x 600， 1x 0 0，x ，算法为：S1 输入工资x （x ≤5 000）；S2 如果x ≤1 600，那么y=0；如果1 600＜x ≤2 100，那么y=0.05（x －1 600）；如果2 100＜x ≤3 600；那么y=25＋0.1（x －2 100）；否则y=175＋15％（x －3 600）；S3 输出税收y ，结束. 流程图如下：12．根据下面的算法画出相应的流程图. 算法：S1 T ←0； S2 I ←2； S3 T ←T+I ； S4 I ←I+2；S5 如果I 不大于200，转S3；S6 输出T ，结束. 思路解析：由算法中出现了条件的判断和循环过程，则在画流程图时应采用选择结构和循环结构.★答案★：这是计算2+4+6+…+200的一个算法. 流程图如下：13．已知算法：①指出其功能（用算式表示）.②将该算法用流程图描述.S1 输入X ；S2 若X<0，执行S3；否则执行S6； S3 Y ←X+1； S4 输出Y ； S5 结束；S6 若X=0，执行S7；否则执行S10； S7 Y ←0； S8 输出Y ； S9 结束； S10 Y ←X ； S11 输出Y ； S12 结束.思路解析：由上面算法可知，当输入的x 的值小于0时，Y=X + 1，当输入的x 的值等于0时，Y=0，而当输入的x 的值大于0时,Y=X ，则此算法是一个根据输入的x 的值求分段函数的函数值的算法，由于在此算法中出现了条件判断，则画流程图时应采用选择结构.★答案★:这是一个输入x 的值，求y 值的算法.其中⎪⎩⎪⎨⎧>=<+=0．x 0，x 0，0， x 1x ，，x y 流程图如下：我创新我超越14．图5-20所示的流程图表示了一个什么样的算法呢？你能用当型循环写出它的算法及流程图吗？图5-20思路解析：由流程图可知此流程图含有一个循环结构，又由流程图可知当条件不成立时进入循环结构，则此循环结构是一个直到型循环结构，这个算法是一个求10个数的平均数的算法.★答案★:这是一个计算10个数的平均数的算法.当型循环的算法如下：S1 S←0；S2 I←1；S3 如果I大于10，转S7；S4 输入G；S5 S←S+G；S6 I←I+1，转S3；S7 A ←S/10；S8 输出A.流程图：。

江苏省宿迁市沭阳县正德中学高中数学1.2 流程图学案（无答案）苏教版必修3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省宿迁市沭阳县正德中学高中数学1.2 流程图学案（无答案）苏教版必修3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省宿迁市沭阳县正德中学高中数学1.2 流程图学案（无答案）苏教版必修3的全部内容。

流程图教学要求：了解解流程图的三种基本逻辑结构，会用流程图表示简单的常见问题的算法；2015年考试说明要求A。

知识点回顾：1。

顺序结构：_________________________________________2。

选择结构:__________________________________________3.循环结构：__________________________________________基础训练：1．（2010年江苏）右图是一个算法的流程图，则输出S的值是__________2.(2013江西)阅读如下程序框图，如果输出5i=，那么在空白矩形框中应填入的语句为_______________典型例题:例1。

（2014新课标）执行下图的程序框图,若输入的,,a b k分别为3,2,1，则输出的M=________例2. 若某程序框图如图所示,则该程序运行后输出的值为．例3。

（2013新课标）运行如下程序框图，如果输入的[1,3]t ∈-，则输出s 属于A ．[3,4]-B ．[5,2]-C ．[4,3]-D ．[2,5]-例4.(2014湖南）设a 是一个各位数字都不是0且没有重复数字的三位数。