鲁教版(五四制)九年级数学下学期《5.7 切线长定理》同步练习

鲁教版（五四制）九年级数学下册第五章圆同步训练考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图：点A，B，C都在⊙O上，且点C在弦AB所对的优弧上，若∠AOB＝72°，则∠ACB的度数是（）A．18°B．30°C．36°D．72°2、如图，已知AB和CD是⊙O的两条等弦，OM⊥AB、ON⊥CD，垂足分别为M、N，BA、DC的延长线交于点P，连接OP．下列四个说法：①AB=CD；②OM=ON；③PA=PC；④∠BPO=∠DPO；正确的个数是（）A．1 B．2 C．3 D．4①0.01的立方根是0.000001；②如果一个角的两边分别平行于另一个角的两边，则两个角一定相等；③正三角形既是中心对称又是轴对称图形；④顺次连接对角线相等的四边形四边中点所得的四边形必是矩形；⑤三角形的内心到三角形的三个顶点的距离相等A ．0个B ．1个C ．2个D ．3个4、如图，△ABC 为等腰直角三角形，∠BAC ＝90°，AB ＝AC ＝2，点D 为△ABC 所在平面内一点，∠BDC ＝90°，以AC 、CD 为边作平行四边形ACDE ，则CE 的最小值为（ ）A B ．3C ．75 D ．5、如图，将线段OA 绕点O 逆时针旋转45°，得到线段OB ．若OA ＝8，则点A 经过的路径长度为（ ）A ．4πB ．3πC ．2πD ．πA．三点确定一个圆B．任何三角形有且只有一个内切圆C．相等的圆心角所对的弧相等D．正多边形一定是中心对称图形7、如图，AB是⊙O的直径，CD是弦，若∠BCD=34°，则∠ABD等于（）A．66°B．34°C．56°D．68°8、如图，A，B，C为⊙O上三点，若∠ABC＝44°，则∠OAC的度数为（）A．46°B．44°C．40°D．50°∥交O于点D，点C、D 9、如图，AB是O的直径，点C在O上，连接AC、BC，过点O作OD AC∠的度数是（）在AB的异侧．若24∠=︒，则BCDBA．66°B．67°C．57°D．48°10、如图，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位:度)，点P运动的时间为x（单位:秒），那么表示y与x关系的图象是( )A ．B ．C ．D ．第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图所示，四边形ABCD 内接于O ，如果它的一个外角∠DCE ＝65︒，那么∠BOD 等于______．2、如图，ABC 和CDE △都是等边三角形，AB CD >，6AB =，固定ABC ，把CDE △绕点C 旋转任意角度，连接AD ，BE ，设AD ，BE 所在的直线交于点O ，则在旋转过程中，始终有AD BE =，且AOB ∠的大小保持不变，这时点O 到直线AB 的最大距离为______．3、如图，已知正方形ABCD，点M是边BA延长线上的动点（不与点A重合），且AM＜AB，△CBE由△DAM平移得到．若过点E作EH⊥AC，H为垂足，则有以下结论：①点M位置变化，使得∠DHC＝60°时，2BE＝DM；②无论点M运动到何处，都有DM；③无论点M运动到何处，∠CHM一定等于150°；④无论点M运动到何处，都有S△ACE＝2S△ADH．其中正确结论的序号为______．4、如图，在O内接四边形ABCD中，若55∠=，则∠DAB＝__________°．BCD5、某圆锥的底面圆半径为1，母线长为2，则该圆锥的侧面积是_____．三、解答题（5小题，每小题10分，共计50分）1、如图，⊙O是△ABC的外接圆，BC为⊙O的直径．(1)尺规作图：作∠ABD＝∠ABC，与⊙O交于点D（保留作图痕迹，不写作法）；(2)在（1）的条件下，连接CD交AB于点E，已知BD＝35，BE＝7AE，求⊙O的半径长．2、如图，D为⊙O上一点，点C是直径BA延长线上的一点，连接CD，且∠CDA＝∠CBD．(1)求证：CD 是⊙O 的切线；(2)若DC ＝4，AC ＝2，求OC 的长．3、如图所示，每个小方格都是边长为1个单位长度的正方形，Rt ABC 的顶点均在格点上，90ACB ∠=︒，在建立平面直角坐标系后，解答下列问题．(1)点A 坐标为______，点B 坐标为______；(2)将ABC 向左平移4个单位，再向下平移5个单位得到111A B C △，若ABC 内部任意一点(),P a b 随ABC 一起平移，则点P 平移后的对应点1P 坐标为______，1PP 的长为______；(3)将ABC 绕点C 逆时针旋转90°得到222A B C △，在图中画出旋转后的222A B C △，并求出边CB 在旋转过程中所扫过的面积（结果保留π）．4、如图，AB 为⊙O 的直径，D 、E 在⊙O 上，C 是AB 的延长线上一点，且∠CEB =∠D ．(1)判断直线CE 与⊙O 的位置关系，并说明理由；(2)若∠D =35°，则∠C 的度数为______°．5、如图，在Rt ABC 中，90ACB ∠=︒，D 为AB 边上的一点，以AD 为直径的O 交BC 于点E ，交AC 于点F ，过点C 作CG AB ⊥于点G ，交AE 于点H ，过点E 的弦EP 交AB 于点Q （EP 不是直径），点Q 为弦EP 的中点，连结BP ，BP 恰好为O 的切线．(1)求证：BC 是O 的切线；(2)求证：AE 平分CAB ∠；(3)若10AQ =，5EQ =，12HG AG =，求四边形CHQE 的面积．-参考答案-一、单选题1、C【解析】【分析】根据同圆中同弧所对的圆周角等于圆心角的一半，即可求得结果．【详解】∵圆心角∠AOB 与圆周角∠ACB 均对着AB∴11723622ACB AOB∠=∠=⨯︒=︒故选：C【点睛】本题考查了圆周角定理，掌握此定理是解题的关键．2、D【解析】【分析】如图连接OB、OD，只要证明Rt△OMB≌Rt△OND，Rt△OPM≌Rt△OPN即可解决问题．【详解】解：如图连接OB、OD；∵AB=CD，∴AB=CD，故①正确；∵OM⊥AB，ON⊥CD，∴AM=MB，CN=ND，∴BM=DN，∵OB=OD，∴Rt△OMB≌Rt△OND，∴OM=ON，故②正确；∵OP=OP，∴Rt△OPM≌Rt△OPN，∴PM=PN，∠OPB=∠OPD，故④正确；∵AM=CN，∴PA=PC，故③正确，综上，四个选项都正确，故选：D．【点睛】本题考查了垂径定理、圆心角、弧、弦的关系、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线面构造全等三角形解决问题．3、A【解析】【分析】根据立方根，中心对称和轴对称图形定义（在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形；一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形是轴对称图形），矩形的判定，三角形内心（三角形内心指三个内角的三条角平分线相交于一点，这个点叫做三角形的内心）逐项判断即可求解．【详解】①0.000001的立方根是0.01，故①错误；②如果一个角的两边分别平行于另一个角的两边，则两个角一定相等或互补，故②错误；③正三角形不是中心对称图形，但是轴对称图形，故③错误；④顺次连接对角线相等的四边形四边中点所得的四边形必是菱形，故④错误；⑤三角形的内心到三角形三边的距离相等，故⑤错误；所以，正确的个数为0个．故选：A【点睛】本题考查了立方根，轴对称图形，中心对称图形，矩形、中点四边形，三角形内心，熟练掌握相关知识点是解题的关键．4、A【解析】【分析】延长AE交BD于点F，根据平行四边形的性质可得AE∥CD，可得∠AFB＝∠BDC＝90°，可以证明△AFB≌△DFE，可得∠AEB＝135°，点E的运动轨迹为圆的运动轨迹，假设点E所在圆的圆心为M，连接MB，MA，MC，MC与圆M交于点E′，根据圆外的点到圆上的点的距离最值可得，CE′即为CE的最小值，利用勾股定理可得CM的值，进而可得CE的最小值．【详解】解：如图，延长AE交BD于点F，连接BE，∵四边形ACDE是平行四边形，∴AE∥CD，AC＝ED，∠EAC＝∠CDE，∵∠BAC＝90°，AB＝AC＝2，∠BDC＝90°，∴ED＝AB＝AC＝2，∠BAF+∠CAE＝90°，∠CDE+∠EDF＝90°，∠AFB＝∠CDB＝∠DFE＝90°，∴BC＝∴∠BAF＝∠EDF，在△AFB 和△DFE 中，BAF EDF AFB DFE AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AFB ≌△DFE （AAS ），∴BF ＝EF ，∴∠BEF ＝45°，∴∠AEB ＝135°，∴点E 的运动轨迹为圆的运动轨迹，假设点E 所在圆的圆心为M ，连接MB ，MA ，MC ，MC 与圆M 交于点E ′，则根据圆外的点到圆上的点的距离最值可得：CE ′即为CE 的最小值，如图，∴∠AMB ＝90°，∵AM ＝BM ，AB ＝2，∴∠MBA ＝45°，BM＝2AB∴∠MBC ＝90°，∴在Rt△MBC 中，MC∴CE ′＝CM ﹣ME ．即CE故选：A ．【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、四点共圆、勾股定理、最短路径问题、等腰直角三角形的性质，解决本题的关键是综合运用以上知识．5、C【解析】【分析】根据题意可得45AOB ∠=︒，再根据弧长公式，即可求解．【详解】解：根据题意得：45AOB ∠=︒，∴点A 经过的路径长度为4582180ππ⨯=． 故选：C【点睛】 本题主要考查了求弧长公式，熟练掌握弧长公式为180n r π（其中n 为圆心角，r 为半径）是解题的关键．6、B【解析】【分析】根据确定圆的条件、三角形的内切圆、圆心角化和弧的关系、中心对称图形的概念判断．【详解】解：A、不在同一直线上的三点确定一个圆，故错误；B、任何三角形有且只有一个内切圆，正确；C、在同圆或等圆中，相等的圆心角所对的弧相等，故错误；D、边数是偶数的正多边形一定是中心对称图形，故错误；故选：B．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．7、C【解析】【分析】由题意根据AB为⊙O的直径，可以得出AB所对弧为半圆，可以得出∠DCB+∠ABD=90°，即可得出答案．【详解】解：∵AB为⊙O的直径，∴∠ADB=90°，∴∠DAB+∠ABD=90°，∵∠DAB=∠BCD=34°，∴∠ABD=90°-34°=56°.故选：C．【点睛】本题主要考查圆周角定理的推论，根据已知可以得出∠DCB+∠ABD=90°是解决问题的关键．8、A【解析】【分析】先利用圆周角定理求出AOC ∠的度数，然后再利用等腰三角形的性质求出OAC ∠即可．【详解】 解：AC 所对的圆周角是ABC ∠，AC 所对的圆心角是AOC ∠，288AOC ABC ∴∠=∠=︒，OA OC =，46OAC OCA ∴∠=∠=︒，故选：A ．【点睛】本题考查了圆周角定理，圆心角、弧、弦的关系，解题的关键是熟练掌握圆周角定理．9、C【解析】【分析】先求出CAO ∠，得出AOD ∠，由等腰三角形的性质和三角形内角和定理求出OAD ∠，再由圆周角定理求出BCD ∠的度数即可．【详解】解：连接AD ，如图所示：//AC OD ，CAO AOD∴∠=∠，AB是O的直径，90ACB∴∠=︒，∴∠CCC=90°−∠C=66°．66AOD∴∠=︒，OA OD=，(180)257OAD AOD∴∠=︒-∠÷=︒，57BCD OAD∴∠=∠=︒；故选：C．【点睛】本题考查了圆周角定理、平行线的性质、等腰三角形的性质，解题的关键是熟练掌握圆周角定理的内容．10、B【解析】【分析】当点P在OC上自O向C运动时，APB∠自90︒逐渐减小到45︒；当点P在CD上运动时，1 245APB AOB∠=∠=︒，为定值；当点P在DO上自D向C运动时，APB∠自45︒逐渐增大到90︒，据此求解即可．【详解】解：如图所示，当点P在OC上自O向C运动时，APB∠自90︒逐渐减小到45︒；当点P在CD上运动时，1245APB AOB∠=∠=︒，为定值；当点P在DO上自D向C运动时，APB∠自45︒逐渐增大到90︒；符合以上变化规律的只有B选项，故选：B．【点睛】本题主要考查动点问题的函数图象，解题的关键是掌握圆周角定理及圆的基本性质．二、填空题1、130°##130度【解析】【分析】根据圆内接四边形对角互补得到∠A+∠BCD=180°，结合∠DCE+∠BCD=180°得到∠A=∠DCE=65°，再由同弧所对圆周角等于圆心角的一半即可求解．【详解】解：由圆内接四边形对角互补可知：∠A+∠BCD=180°，又∠DCE+∠BCD=180°，∴∠A=∠DCE=65°，由同弧所对的圆周角等于圆心角的一半可知：∠BOD=2∠A=130°，故答案为：130°．【点睛】本题考查了圆周角定理及其推论，属于基础题，熟练掌握圆周角定理及其推论是解决本类题的关键．2、【解析】【分析】证明△ACD≌△BCE(SAS) ，作△ABC的外接圆⊙M，则当点O与点C重合时，点O到直线AB的距离最大，最大距离为线段CF的长，勾股定理求解即可【详解】∵△ABC和△CDE都是等边三角形，∴AC = BC, CD = CE，∠BAC=∠ABC=∠ACB=∠DCE，∴∠ACE＋∠DCE=∠ACE＋∠ACB，即∠ACD＝∠BCE，则△ACD≌△BCE(SAS)，∴∠CAD= ∠CBE，∴∠AOB= ∠ACB，作△ABC的外接圆⊙M，如图：则点O在⊙OM上，作OF⊥AB于点F，则当点O与点C重合时，点O到直线AB的距离最大，最大距离为线段CF的长，在Bt△ACF中，30ACF∠=︒AB=3，AF = BF = 12CF即点O到直线AB的最大距离为故答案为：【点睛】本题考查了等边三角形的性质，含30度角的直角三角形的性质，旋转的性质，三角形的外心，作出辅助圆是解题的关键．3、①②④【解析】【分析】①由正方形的性质、平移的特征证明△ADH≌△EMH，再以MD为直径作圆，则该圆经过点A、H，可证明∠BEC＝∠AMD＝∠DHC＝60°，由∠B＝90°，得2BE＝CE＝DM，故①正确；②由①得△DMH是等腰直角三角形，由等腰直角三角形的性质可得到DM，故②正确；③由①得∠CHM的大小随∠DHC 的变化而变化，举一个反例说明∠CHM的大小不是定值150°，故③错误；④过点H作HP⊥AB，HQ⊥AD，设正方形的边长为x，HP的长为a，用含x、a的式子分别表示△ACE和△ADH的面积，即可得出S△ACE＝2S△ADH，故④正确．【详解】解：①如图，在正方形ABCD中，AB＝CB＝AD＝CD，∠B＝∠ADC＝90°，∴∠DAH＝∠BAC＝45°，∵EH⊥AC，∴∠AHE＝90°，∴∠MEH＝∠EAH＝45°＝∠DAH，∴AH＝EH；由平移得AM＝BE，∴EM＝AB＝AD，∴△ADH≌△EMH（SAS），∴∠DHA＝∠MHE，∴∠DHM＝∠DHA﹣∠AHM＝∠MHE﹣∠AHM＝∠AHE＝90°；DM＝OD，以DM的中点O为圆心，以DM为直径作⊙O，连接OA、OH，则OA＝OH＝12∴点A、H在⊙O上．当∠DHC＝60°时，则∠BEC＝∠AMD＝180°﹣∠DHA＝∠DHC＝60°，∴∠BCE＝30°，∴2BE＝CE＝DM．故①正确；②由①得HD＝HM，∠DHM＝90°，∴DM2＝HD2+HM2＝2HM2，∴DM HM．故②正确；③∵∠CHM＝∠DHC+∠DHM＝∠DHC+90°，∴∠CHM的大小随∠DHC即∠AMD的变化而变化，如当∠AMD＝75°时，则∠CHM＝165°≠150°．故③错误；④作HP⊥AB于点P，HQ⊥AD于点Q，则HP＝HQ＝12AE＝AP＝EP．设正方形ABCD的边长为x，HP＝HQ＝a，则AE＝2a．∵S△ACE＝12×2ax＝ax，S△ADH＝12ax，∴S△ACE＝2S△ADH．故④正确．故答案为：①②④．【点睛】本题是四边形的综合题，考查了正方形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，圆内接四边形的性质；掌握正方形的性质、全等三角形的判定和性质是解题的关键．说明一个命题错误要会举反例．【解析】【分析】根据圆内接四边形对角互补即可求解．【详解】解：∵在O内接四边形ABCD中，55BCD∠=，∴∠DAB＝180°-55°=125°故答案为：125【点睛】本题考查了圆内接四边形对角互补，理解圆内接四边形对角互补是解题的关键．5、2π【解析】【分析】由圆锥的侧面积公式即可求解．【详解】解：根据圆锥的侧面积公式：S侧=πrl=π×1×2=2π．故答案为：2π．【点睛】本题主要考查了圆锥侧面积公式．掌握圆锥侧面积公式：S侧=πrl是解决问题的关键．三、解答题1、 (1)见解析(2)45 2【分析】（1）根据同圆或等圆中，相等的弦所对的圆周角相等，只需作弦AD=AC即可．（2）连接OA，交DC于H，可得AO∥BD，O是BC中点，可知OH是BD的一半，可得△BDE∽△AHE，利用性质可求AH长，最后可得半径长．(1)解：如图，以点A为圆心，AC为半径画弧与圆O交于点D，连接BD，则∠ABD即所求．(2)解：如图，连接OA，交DC于H，在⊙O中：设OB＝OA＝OC＝r，∴∠OBA＝∠OAB，r＝OH+HA，∵∠ABD＝∠ABC，∴∠ABD＝∠OAB，∴BD∥OA，∴∠BDC＝∠OHC，∵BC是直径，∴∠BDC＝∠OHC=90°，连接OD，∵OD=OC，OH⊥CD，∴DH=CH，∴H是CD的中点，∵点O是BC的中点，∴OH是△BCD的中位线，∴OH＝12BD＝352，∵BE＝7AE，∴17 AEBE=，∵BD∥OA，∴△BDE∽△AHE，∴1735 AE AH AH BE BD===，∴AH＝5，∴r＝OH+HA＝352+5＝452．∴⊙O的半径长是452．【点睛】本题考查了圆的基本性质，三角形相似的判定和性质，三角形中位线定理，熟练掌握圆的性质，灵活运用相似三角形的性质是解题的关键．2、 (1)见解析(2)5【解析】【分析】（1）根据圆周角定理和等腰三角形的性质，得出∠ODA+∠CDA=90°，即OD⊥CD即可得出结论；（2）利用相似三角形的判定和性质，求出BC，进而求出半径OA，再求出OC即可．(1)解：如图，连接OD，∵AB是⊙O的直径，∴∠ADB=90°，即∠ODB+∠ODA=90°，∵OB=OD，∴∠ABD=∠ODB，又∵∠CDA=∠CBD，∴∠ODA+∠CDA=90°，即OD⊥CD，∵OD 是⊙O 的半径，∴CD 是⊙O 的切线；(2)∵∠CDA =∠CBD ，∠ACD =∠DCB ，∴△ACD ∽△DCB ， ∴CD AC CB DC=， 即424CB =， ∴CB =8，∴OA =2CB AC -=822-=3， ∴OC =OA +AC=3+2=5．【点睛】本题考查圆周角定理，等腰三角形的性质以及相似三角形的判定和性质，掌握圆周角定理，相似三角形的性质是解决问题的关键．3、 (1)（1，4）；（3，1）；(2)（a -4,b -5）(3)图形见详解，π．【解析】【分析】（1）根据图形所在平面直角坐标系中的位置即可点A 、点B 的坐标；（2）根据点平移特征左减右加，上加下减，求出平移后坐标A 1（-3,-1），B 1（-1,-4），C 1（-3,-4），描点画出111A B C △，根据点P ，求出P 1坐标，利用平移距离求出AA 1即可；（3）利用直角三角形绕着直角顶点旋转特征画出图形，利用扇形面积公式求出CB 扫过面积即可．(1)解：根据△ABC 所在位置，点A 的坐标为（1，4），点B 的坐标为（3，1），故答案为（1，4）；（3，1）；(2)解：将ABC 向左平移4个单位，再向下平移5个单位得到111A B C △，∵点A （1，4），B （3，1），C （1，1），根据坐标平移的特征，左减右加，上加下减，∴平移后A 1（1-4,4-5），B 1（3-4,1-5），C 1（1-4,1-5）即A 1（-3,-1），B 1（-1,-4），C 1（-3,-4）， 在平面直角坐标系中描点A 1（-3,-1），B 1（-1,-4），C 1（-3,-4），顺次连结A 1B 1，B 1C 1，C 1A 1，则111A B C △是平移后的三角形，点(),P a b 平移后P 1（a -4,b -5），PP 1=AA 1222213414541，故答案为（a -4,b -5）(3)解：∵△ABC 是直角三角形，旋转中心为直角顶点点C ，在BC 延长线上，截取CA 2=CA ，在CA 上，截取CB 2=CB ，连结A 2B 2，则222A B C △为△ABC 绕点C 逆时针旋转90°的三角形，扇形CBB 2为边CB 在旋转过程中所扫过的面积，CB =3-1=2，∠BCB 2=90°，∴CBB S 1扇形 =ππ2124．【点睛】本题考查网格作图，图形与坐标，勾股定理，图形平移与旋转，圆面积，掌握网格作图，图形与坐标，勾股定理，图形平移与旋转，圆面积是解题关键．4、 (1)CE 与⊙O 相切，理由见解析(2)20【解析】【分析】（1）连接OE ，由圆周角定理证得∠EAB +∠EBA =90°，由已知和等腰三角形的性质证得∠EAB =∠CEB ，∠OEB =∠OBE ，进而证得∠OEC =90°，根据切线的判定定理即可证得CE 与⊙O 相切；（2）先求出∠CEB =∠EAB =35°，进而求出∠EBA =55°，再根据三角形外角的性质即可求出∠C ．(1)证明：CE 与⊙O 相切，理由如下：连接OE ，∵AB为⊙O的直径，∴∠AEB=90°，∴∠EAB+∠EBA=90°，∵∠EAB=∠D，∠CEB=∠D，∴∠EAB=∠CEB，∵OE=OB，∴∠OEB=∠OBE，∴∠OEC=∠OEB+∠CEB=∠EBA+∠EAB=90°，∵OE是⊙O的半径，∴CE与⊙O相切；(2)解：由（1）知∠EAB+∠EBA=90°，∵∠EAB=∠D=35°，∴∠EBA=90°-35°=55°，∠CEB=∠D=35°，∵∠EBA=∠CEB+∠C，∴∠C=∠EBA-∠CEB=55°-35°=20°，故答案为：20．【点睛】本题主要考查了切线的判定，圆周角定理，三角形的外角定理，根据圆周角定理∠CEB =∠EAB 是解决问题的关键．5、 (1)见解析(2)见解析(3)20【解析】【分析】（1）连接OE ，OP ，证明BEO △≌BPO △，可得BEO BPO ∠=∠，进而证明BC 是O 的切线；（2）由90BEO ACB ∠=∠=︒，可得//AC OE ，进而可得CAE OEA ∠=∠，由OA OE =得EAO OEA ∠=∠，进而可得∠CAE EAO =∠，即AE 平分CAB ∠（3）由（1）得：EP AB ⊥，证明//CG EP ，得QEH CHE ∠=∠，证明ACE ≌AQE （AAS ），四边形CHQE 是菱形，设HG x =，则2AG x =，102GQ x =-，在Rt QHG △中，勾股定理建立方程，解方程进而求得四边形CHQE 的面积．(1)连接OE ，OP ，∵AD 为直径，点Q 为弦EP 的中点，∴AB 垂直平分EP ，∴BP BE =，∵OE OP =，OB OB =， ∴BEO △≌BPO △， ∴BEO BPO ∠=∠， ∵BP 为O 的切线， ∴OP BP ⊥， ∴90BPO ∠=︒， ∴90BEO ∠=︒， ∴OE BC ⊥于点E ， ∵OE 是O 的半径， ∴BC 是O 的切线．(2)∵90BEO ACB ∠=∠=︒， ∴//AC OE ，∴CAE OEA ∠=∠， ∵OA OE =，∴EAO OEA ∠=∠， ∴∠CAE EAO =∠， ∴AE 平分CAB ∠．(3)由（1）得：EP AB ⊥， ∴90AQE ∠=︒． ∵CG AB ⊥，∴90CGA ∠=︒，∴90CGA AQE ∠=∠=︒，∴//CG EP ，即//CH EP ．∴QEH CHE ∠=∠．∵90ACE AQE ∠=∠=︒，AE AE =，由（2）得CAE EAO ∠=∠，∴ACE ≌AQE （AAS ），∴CEH QEH ∠=∠，CE QE =，∴CEH CHE ∠=∠，∴CH CE =，∴5CH QE ==，∵CH EP ∥，∴四边形CHQE 是平行四边形．∵CH CE =，∴四边形CHQE 是菱形，∴5QH EQ ==．设HG x =，则2AG x =，102GQ x =-，在Rt QHG △中，根据勾股定理得：222HG GQ QH +=，∴()2221025x x +-=，解得13x =，25x =（不合题意，舍去）．∴3HG =，1024GQ x =-=．∴四边形CHQE 的面积5420CH GQ =⋅=⨯=．【点睛】本题考查了切线的性质与判定，平行线的性质与判定，三角形全等的性质与判定，菱形的性质与判定，勾股定理，掌握以上知识是解题的关键．。

第 2 章 对称图形 —— 圆第 4 课时 切线长定理知识点 切线长定理的应用1． 如图 2－ 5－ 32，PA ，PB 分别切⊙ O 于 A ， B 两点．若∠ P ＝60° ， PA ＝ 2，则弦 AB的长为 ()A ． 1B ．2C ． 3D ． 4图 2－ 5－32图 2－ 5－33.如图 2－5－ 33， CD 是⊙ O 的切线 ，切点为 E ， AC ， BD 分别与⊙ O 相切于点 A ， B.如果 CD ＝7， AC ＝ 4，那么 BD 等于 ()A ． 5B ．4C ． 3D ． 23． [教材习题 2.5 第 13 题变式 ]如图 2－ 5－ 34，四边形 ABCD 的边AB ， BC ，CD ， DA 和⊙ O 分别相切．若四边形ABCD 的周长为 20，则 AB ＋ CD 等于 ()A ． 5B ． 8C ． 10D ．12︵4． 已知线段 PA ， PB 分别切⊙ O 于点 A ， B ，AB120°， ⊙ O 的半径为 4，则的度数为 线段 AB 的长为 ()A ． 8B ． 43C ． 6 3D ． 83图 2－ 5－34图 2－ 5－35.如图 2－5－ 35， PA， PB 是⊙ O 的切线，A ， B 为切点， AC 是⊙ O 的直径，∠P＝ 40°，则∠ BAC 的度数为 ________．6．如图 2－ 5－ 36，PA ， PB 分别切⊙ O 于点 A ， B ，∠ AOP ＝50°，则∠PAB ＝ ________°，∠ OPB＝ ________°.图2－ 5－36图2－ 5－377．如图 2－ 5－ 37，PA ， PB， DE 分别切⊙ O 于点 A， B， C，若⊙ O 的半径为5， OP＝13，则△ PDE 的周长为 ________．图2－ 5－388．如图 2－ 5－ 38，P 是⊙ O 的直径 AB 的延长线上一点， PC， PD 分别切⊙ O 于点C，D. 若 PA ＝ 6，⊙O 的半径为 2，则∠ CPD 的度数为 ________．9．如图 2－ 5－ 39，PA ， PB 为⊙ O 的两条切线， A ， B 为切点．若是⊙ O 的半径为5，∠OPA ＝ 30°，求两条切线的夹角∠APB 的度数及切线PA 的长．图2－ 5－39图 2－ 5－40 10． [2016 ·梁溪区一模 ]AB ＝ 4， AD ＝ 5，AD ， AB ， BC 分别与⊙BC 于点 M ，切点为 N ，则 DM 的长为 (O 相切于点)如图2－5－40，在矩形ABCD 中，E，F， G，过点 D 作⊙ O 的切线交139 A. 34 13C. 39D． 2511．如图 2－ 5－ 41， PA， PB 是⊙ O 的切线， A ， B 为切点， AC 是⊙ O 的直径，∠ ACB ＝ 70°.求∠ P 的度数．图2－ 5－4112．如图 2－ 5－ 42，△ ABC 的内切圆⊙ O 与 AC ， AB ， BC 分别相切于点D， E， F，且AB ＝5 cm， BC＝ 9 cm， AC ＝ 6 cm，求 AE ， BF 和 CD 的长．图2－ 5－4213．如图 2－ 5－ 43， PA， PB 为⊙ O 的两条切线，切点分别为 A ，B ，直线 CD 切⊙ O 于点 E.(1)试试究△ PCD 的周长与线段 PA 的数量关系；(2)若∠ P＝α，求∠ COD 的度数．图2－ 5－4314．如图 2－ 5－ 44， AB 是⊙ O 的直径， AM ， BN 分别切⊙ O 于点 A ， B， CD 分别交AM ， BN 于点 D ，C， DO 均分∠ ADC.(1)求证： CD 是⊙ O 的切线；(2)若 AD ＝ 4， BC＝9，求⊙ O 的半径 R.图2－ 5－4415．如图 2－ 5－ 45， PA， PB 分别与⊙ O 相切于点 A ， B，点 M 在 PB 上，且OM ∥ AP， MN ⊥ AP，垂足为 N.(1)求证： OM ＝ AN ；(2)若⊙ O 的半径 R＝ 3， PB＝ 9，求 OM 的长．图2－ 5－ 45详解详析1． B2． C3． C4． B5． 20°[ 剖析 ]∵ PA，PB是⊙ O的切线，A，B为切点，1∴PA ＝ PB，∴∠ BAP ＝∠ ABP ＝2×(180° － 40° )＝ 70° .由 PA 是⊙ O 的切线， A 为切点，AC 是⊙ O 的直径，得∠ PAC ＝ 90°，∴∠ BAC ＝90° － 70°＝20°. 6． 50 407． 24 [ 剖析 ]∵ PA，PB，DE分别切⊙ O于A，B，C三点，∴AD ＝ CD ， CE＝ BE ， PA＝ PB，OA ⊥ PA.在Rt△ OAP 中，依照勾股定理，得 AP ＝ 12，∴△ PDE 的周长为PD＋ DE＋ PE＝ PD＋ AD ＋ BE ＋ PE＝ 2PA ＝ 24.8． 60°[ 剖析 ] 连接 OC.∵ PA＝ 6，⊙O 的半径为2，∴OP＝ PA － OA ＝4.∵PC， PD 分别切⊙ O 于点 C，D ，∴∠ OPC＝∠ OPD， OC⊥ PC.∵OP＝ 2OC，∴∠ OPC＝ 30°，∴∠ CPD＝60° .9．解：连接 OA ， OB，则 OA ⊥PA， OB ⊥ PB.∵OA ＝ OB ，OP＝ OP，∴Rt△ OAP≌ Rt△ OBP ，∴∠ OPA＝∠ OPB，∴∠ APB ＝2∠ OPA＝ 60° .在Rt△ AOP 中，可求得 OP＝ 2OA ＝ 10，∴PA＝ OP2－ OA 2＝5 3.10． A [剖析 ] 如图，连接 OE， OF，ON ， OG.在矩形 ABCD 中，∠ A ＝∠ B ＝ 90°， CD ＝ AB ＝ 4.∵ AD ， AB ，BC 分别与⊙ O 相切于点 E， F，G，∴∠ AEO ＝∠ AFO ＝∠ OFB＝∠ BGO ＝ 90°.又∵ OE＝ OF＝ OG，∴四边形AFOE ，四边形 FBGO 是正方形，∴AF ＝ BF＝ AE ＝ BG ＝2，∴DE ＝ 3.∵ DM 是⊙ O 的切线，∴DN ＝ DE ＝3， MN ＝ MG ，∴CM ＝5－ 2－ MG ＝ 3－ MN.在Rt△ DMC 中， DM 2＝ CD2＋ CM 2，∴ (3＋ MN) 2＝ 42＋ (3－ MN) 2，4 4 13∴MN ＝3，∴ DM ＝ 3＋3＝3.应选 A.11．解：连接 AB.∵AC 是⊙ O 的直径，∴∠ CBA ＝ 90°，∴∠ BAC ＝ 90° －∠ ACB ＝ 20° .∵PA ， PB 是⊙ O 的切线，∴PA ＝ PB，∠ CAP＝ 90°，∴∠ PAB ＝90° － 20°＝ 70°.∵PA ＝ PB，∴∠ PBA ＝∠ PAB ＝ 70°，∴∠ P＝180° －∠ PAB －∠ PBA ＝ 40°.12．解：∵⊙ O 与△ ABC 的三边都相切，∴AE ＝ AD ，BE ＝ BF ，CD ＝ CF.设AE ＝ x cm， BF＝ y cm， CD＝z cm，x＋ y＝ 5，x＝1，{y＋z＝9，) {y＝4，)则 z＋ x＝ 6，解得z＝ 5.即AE ＝ 1 cm， BF＝ 4 cm， CD＝5 cm.13．解： (1) △ PCD 的周长＝ 2PA. 原由以下：∵ PA ， PB 分别切⊙ O 于点 A ， B ，CD 切⊙ O 于点 E，∴PA ＝ PB， AC ＝ CE， BD ＝ DE，∴△ PCD 的周长＝ PD＋DE ＋ PC＋ CE＝ PB＋ PA＝ 2PA ，即△ PCD 的周长＝ 2PA.(2)如图，连接 OA， OE， OB.由切线的性质，得OA⊥ PA，OB⊥PB，OE⊥ CD，BD＝DE，AC＝CE.∵OA ＝ OE＝OB ，易证△ AOC ≌△ EOC ，△EOD ≌△ BOD ，∴∠ AOC ＝∠ EOC，∠ EOD＝∠ BOD ，11∴∠ COD ＝∠ EOC＋∠ EOD＝ 2(∠ AOE ＋∠ BOE) ＝ 2∠ AOB.∵∠ P＝α，OA ⊥ PA， OB⊥PB ，∴∠ AOB ＝ 180°－α，1∴∠ COD ＝ 90°－2α.14 解： (1)证明：如图，过点 O 作 OE⊥ CD 于点 E.∵ AM 切⊙ O 于点 A，∴OA ⊥ AD.又∵ DO 均分∠ ADC ，∴OE＝ OA.∵ OA 为⊙ O 的半径，∴OE 是⊙ O 的半径，∴CD 是⊙ O 的切线．(2) 过点 D 作 DF⊥ BC 于点 F.∵ AM ，BN 分别切⊙ O 于点 A， B，∴AB ⊥ AD ，AB ⊥ BC，∴四边形 ABFD 是矩形，∴AD ＝ BF ， AB ＝ DF.又∵ AD ＝4， BC ＝ 9，∴ FC＝ 9－ 4＝5.∵AM ，BN ， DC 分别切⊙ O 于点 A ， B， E，∴ AD ＝ DE ，BC＝ CE，∴CD ＝ DE ＋ CE＝AD ＋ BC ＝ 4＋9＝13. 在 Rt△ DFC 中， CD2＝ DF2＋ FC2，∴DF ＝ CD2－ FC2＝ 12，∴AB ＝ 12，∴⊙ O 的半径 R 为 6.15．解： (1) 证明：如图，连接 OA ，则 OA ⊥PA.∵MN ⊥PA ，∴ MN ∥OA.∵OM ∥PA ，∴四边形ANMO 是平行四边形．又∵ MN ⊥ AP，∴?ANMO 是矩形，∴OM ＝AN.(2)如图，连接 OB，则 OB⊥ PB，∴∠ OBM ＝∠ MNP ＝ 90° .∵四边形ANMO 是矩形，∴OA ＝ MN.又∵ OA ＝OB ，∴OB ＝ MN.∵OM ∥AP ，∴∠ OMB ＝∠ MPN ，∴△ OBM ≌△ MNP ，∴ OM ＝ MP.设OM ＝x，则 MP＝ x， AN ＝ x.∵PA ＝ PB＝ 9，∴NP ＝9－ x.在Rt△ MNP 中，有 x2＝ 32＋ (9－ x)2，解得 x＝ 5，即 OM ＝ 5.。

切线长定理同步练习一、选择题（共10小题，每小题4分，共40分）1. 如图，P 为⊙O 外一点，PA ，PB 是⊙O 的切线，切点分别为A ，B ，若PA ＝5，则PB 的长是( )A ．2B ．3C ．4D ．52. 如图，PA 、PB 为圆O 的切线，切点分别为A 、B ，PO 交AB 于点C ，PO 的延长线交圆O 于点D ，下列结论不一定成立的是( )A ．PA ＝PB B ．∠BPD ＝∠APDC ．AB ⊥PD D ．AB 平分PD3. 如图，PA 切⊙O 于点A ，PB 切⊙O 于点B ，OP 交⊙O 于点C ，下列结论中，错误的是( )A ．∠1＝∠2B ．PA ＝PBC ．AB ⊥OPD ．∠PAB ＝2∠14.如图，PA ，PB 为⊙O 的切线，A ，B 分别为切点，∠APB ＝60°，点P 到圆心O 的距离OP ＝2，则⊙O 的半径为( )A ．12B ．1C ．32D ．2 5.如图，AB 是⊙O 的直径，点C 为⊙O 外一点，CA ，CD 是⊙O 的切线，A ，D 为切点，连接BD ，AD.若∠ACD ＝30°，则∠DBA 的大小是( )A ．15°B ．30°C ．60°D ．75°6. 一把直尺、含60°角的直角三角尺和光盘如图摆放，AB ＝3，则光盘的直径是( )A ．3B ．3 3C ．6D ．6 37. 如图，PA 、PB 分别与⊙O 相切于A 、B 两点，点C 为⊙O 上一点，连接AC 、BC ，若∠P ＝50°，则∠ACB 的度数为( )A ．60°B ．75°C ．70°D ．65°8. 如图，从⊙O 外一点P 引圆的两条切线PA 、PB ，切点分别为A 、B ，点C 是劣弧AB 上一点，过点C 的切线分别交PA 、PB 于点M ，N ，若⊙O 的半径为2，∠P ＝60°，则△PMN 的周长为( )A ．4B ．6C ．4 3D ．6 39. 如图，在矩形ABCD 中，AB ＝4，AD ＝5，AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点，过点D 作⊙O 的切线交BC 于点M ，切点为N ，则DM 的长为( )A.133B.92C.4313 D ．2 5 10. 如图，AB 为半圆O 的直径，AD ，BC 分别切半圆O 于A ，B 两点，CD 切半圆O 于点E ，AD 与CD 交于点D ，BC 与CD 交于点C ，连接OD 、OC ，下列结论：①AD ＋BC ＝CD ；②OD ＝OC ；③S 梯形ABCD ＝12CD·OA ；④∠DOC ＝90°.其中正确的有( )A ．①④B ．①②③C ．②③④D ．③④二．填空题（共6小题，每小题4分，共24分）11.如图，PA ，PB 切⊙O 于点A ，B ，已知∠APB ＝60°，⊙O 的半径为2，则切线PA 的长为_______．12. 如图，AB ，AC ，BD 是⊙O 的切线，P ，C ，D 为切点，如果AB ＝5，AC ＝3，则BD 的长为_______．13. 如图，PA ，PB 是⊙O 的切线，切点分别为A ，B ，点C 在AB ︵上，过点C 的切线分别交PA ，PB 于点E ，F.若△PEF 的周长为6，则线段PA 的长为________．14. 如图，在四边形ABCD 中，AB ＝16，CD ＝10，AB ，BC ，CD ，AD 与⊙O 分别相切于点E ，F ，G ，H ，则四边形ABCD 的周长为______．15. 如图，PA ，PB 分别切⊙O 于点A ，B ，点C 在⊙O 上，且∠ACB ＝50°，则∠P ＝______．16. 如图，在△ABC 中，∠C ＝90°，AC ＝3，BC ＝4，则△ABC 的内切圆半径r ＝________．三．解答题（共6小题， 56分）17．(6分) 如图，四边形ABCD的各边与⊙O分别相切于点E，F，G，H，说明AB＋CD 与BC＋AD的大小关系.18．(8分) 如图，PA，PB是⊙O的切线，A，B为切点，CD切⊙O于点E，连接OC，OD，△PCD的周长为12，∠P＝60°.求PA的长.19．(8分) 如图，PA，PB是⊙O的两条切线，A，B是切点，若∠APB＝60°，PO＝2，求⊙O的半径的长.20．(10分) 如图，已知AB为⊙O的直径，PA，PC是⊙O的切线，A，C为切点，∠BAC ＝30°.求∠P的大小.21．(12分) 已知：AB是⊙O的直径，AB＝2，弦DE＝1，直线AD与BE相交于点C，弦DE在⊙O上运动且保持长度不变，过点D的切线交BC于点F.若DE∥AB，求证：CF＝EF；22．(12分) 如图，直线AB，BC，CD分别与⊙O相切于点E，F，G，且AB∥CD，OB＝6 cm，OC＝8 cm.求：(1)∠BOC的度数；(2)BE＋CG的长；(3)⊙O的半径．参考答案1-5DDDBD 6-10DDCAA11．2 312．213．314．5215．80°16. 117. 解：由切线长定理，得AE ＝AH ，BE ＝BF ，CF ＝CG ，DG ＝DH ，∴AB ＋CD ＝AE ＋BE ＋CG ＋DG ＝AH ＋BF ＋CF ＋DH ＝AH ＋DH ＋BF ＋CF ＝BC ＋AD ，即AB ＋CD ＝BC ＋AD.18. 解：∵CA ，CE 都是⊙O 的切线，∴CA ＝CE ，同理DE ＝DB ，PA ＝PB ，∴△PDC 的周长＝PD ＋CD ＋PC ＝PD ＋PC ＋CA ＋BD ＝PA ＋PB ＝2PA ＝12，即PA 的长为619. ∵PA ，PB 是⊙O 的两条切线，∴∠APO ＝∠BPO ＝12∠APB ，∠PAO ＝90°.∵∠APB ＝60°，∴∠APO ＝30°.∵PO ＝2，∴AO ＝1.20. 解：∵PA 是⊙O 的切线，AB 为⊙O 的直径，∴PA ⊥AB ，∴∠BAP ＝90°.∵∠BAC ＝30°，∴∠CAP ＝90°－∠BAC ＝60°.又∵PA ，PC 切⊙O 于点A ，C ，∴PA ＝PC ，∴△PAC 为等边三角形，∴∠P ＝60°21. 证明：连接OD ，OE.∵AB ＝2，∴OA ＝OD ＝OE ＝OB ＝1.∵DE ＝1，∴OD ＝OE ＝DE.∴△ODE 是等边三角形.∴∠ODE ＝∠OED ＝60°.∵DE ∥AB ，∴∠AOD ＝∠ODE ＝60°，∠BOE ＝∠OED ＝60°.∴△AOD 和△BOE 都是等边三角形．∴∠OAD ＝∠OBE ＝60°. ∵DE ∥AB ，∴∠CDE ＝∠OAD ＝60°，∠CED ＝∠OBE ＝60°.∴△CDE 是等边三角形.∵DF 是⊙O 的切线，∴DF ⊥OD.∴∠ODF ＝90°.∴∠EDF ＝90°－∠CED ＝90°－60°＝30°.∴∠DFE ＝180°－∠EDF －∠CED ＝180°－30°－60°＝90°.∴DF ⊥CE.∴CF ＝EF.22. 解：(1)连接OF ，根据切线长定理，得BE ＝BF ，CF ＝CG ，∠OBF ＝∠OBE ，∠OCF ＝∠OCG.∵AB ∥CD ，∴∠ABC ＋∠BCD ＝180°，∴∠OBF ＋∠OCF ＝90°，∴∠BOC ＝90°(2)由(1)知，∠BOC ＝90°.∵OB ＝6 cm ，OC ＝8 cm ，∴由勾股定理，得BC ＝OB 2＋OC 2 ＝10 cm ，∴BE ＋CG ＝BC ＝10 cm(3)∵OF ⊥BC ，∴OF ＝OB·OC BC ＝4.8 cm。

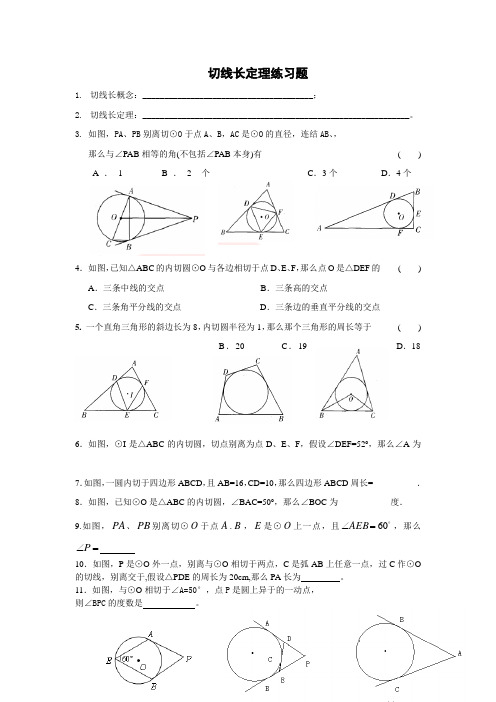
切线长定理练习题1. 切线长概念：_______________________________________；2. 切线长定理：_____________________________________________________________。

3. 如图，PA 、PB 别离切⊙O 于点A 、B ，AC 是⊙O 的直径，连结AB 、，那么与∠PAB 相等的角(不包括∠PAB 本身)有 ( )A ． 1B ．2个C ．3个D ．4个4． 如图，已知△ABC 的内切圆⊙O 与各边相切于点D 、E 、F ，那么点O 是△DEF 的 ( )A ．三条中线的交点B ．三条高的交点C ．三条角平分线的交点D ．三条边的垂直平分线的交点5. 一个直角三角形的斜边长为8，内切圆半径为1，那么那个三角形的周长等于 ( )B ．20C ．19D ．186．如图，⊙I 是△ABC 的内切圆，切点别离为点D 、E 、F ，假设∠DEF=52o ，那么∠A 为_____7．如图，一圆内切于四边形ABCD ，且AB=16，CD=10，那么四边形ABCD 周长=__________．8．如图，已知⊙O 是△ABC 的内切圆，∠BAC=50o ，那么∠BOC 为____________度．9.如图，PA 、PB 别离切⊙O 于点A .B ，E 是⊙O 上一点，且 60=∠AEB ，那么=∠P ____ 10．如图，P 是⊙O 外一点，别离与⊙O 相切于两点，C 是弧AB 上任意一点，过C 作⊙O 的切线，别离交于,假设△PDE 的周长为20cm,那么PA 长为 。

11．如图，与⊙O 相切于∠A=50°，点P 是圆上异于的一动点，则∠BPC 的度数是 。

PBAO12. 如图，PA、PB是⊙O的两条切线，切点别离为点A、B，假设直径AC= 12，∠P=60o，求弦AB的长．13.如图，PA、PB是⊙O的切线A、B为切点，∠OAB＝30°。

5.7 切线长定理一．选择题1．如图，P A，PB分别切⊙O与点A，B，MN切⊙O于点C，分别交P A，PB于点M，N，若P A＝7.5cm，则△PMN的周长是（）A．7.5cm B．10cm C．12.5cm D．15cm2．如图，⊙O内切于正方形ABCD，O为圆心，作∠MON＝90°，其两边分别交BC，CD 于点N，M，若CM+CN＝4，则⊙O的面积为（）A．πB．2πC．4πD．0.5π3．如图，四边形ABCD是⊙O的外切四边形，且AB＝10，CD＝12，则四边形ABCD的周长为（）A．44B．42C．46D．474．如图，AB、AC、BD是⊙O的切线，切点分别是P、C、D．若AB＝5，AC＝3，则BD 的长是（）A．4B．3C．2D．15．如图，一个菱形的边长与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿此菱形的四边做无滑动旋转，直至回到原出发位置时，这个圆共转了（）A．6圈B．5圈C．4.5圈D．4圈6．如图，⊙O是四边形ABCD的内切圆，下列结论一定正确的有（）个：①AF＝BG；②CG＝CH；③AB+CD＝AD+BC；④BG＜CG．A．1B．2C．3D．4二．填空题7．如图，从点P引⊙O的切线P A，PB，切点分别为A，B，DE切⊙O于C，交P A，PB于D，E．若△PDE的周长为20cm，则P A＝cm．8．如图，⊙O是四边形ABCD的内切圆，连接OA、OB、OC、OD．若∠AOB＝108°，则∠COD的度数是．9．如图，菱形ABCD，∠B＝60°，AB＝4，⊙O内切于菱形ABCD，则⊙O的半径为．10．以正方形ABCD的AB边为直径作半圆O，过点C作直线切半圆于点F，交AD边于点E，若△CDE的周长为12，则直角梯形ABCE周长为．11．如图，P A，PB是⊙O的切线，A，B为切点，∠OAB＝38°，则∠P＝°．12．如图，四边形ABCD是⊙O的外切四边形，且AB＝10，CD＝12，则四边形ABCD的周长为．13．已知：P A切⊙O于点A，PB切⊙O于点B，点C是⊙O上异于A、B的一点，过点C 作⊙O的切线分别交P A和PB于点D、E，若P A＝10cm，DE＝7cm，则△PDE的周长为cm．14．如图所示，P为⊙O外一点，P A、PB分别切⊙O于A、B，CD切⊙O于点E，分别交P A、PB于点C、D，若P A＝15，则△PCD的周长为．15．如图，△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，已知AD＝10cm，小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形（△AMN），则剪下的△AMN的周长为．16．如果圆的外切四边形的一组对边的和是5cm，那么这个四边形的周长是cm．三．解答题17．如图，P A、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠BAC＝20°，求∠P 的度数．18．如图，AB为⊙O直径，P A、PC分别与⊙O相切于点A、C，PQ⊥P A，PQ交OC的延长线于点Q．（1）求证：OQ＝PQ；（2）连BC并延长交PQ于点D，P A＝AB，且CQ＝6，求BD的长．19．如图，∠APB＝52°，P A、PB、DE都为⊙O的切线，切点分别为A、B、F，且P A＝6．（1）求△PDE的周长；（2）求∠DOE的度数．20．如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，OB＝6cm，OC＝8cm．求：（1）∠BOC的度数；（2）BE+CG的长；（3）⊙O的半径．21．已知P A、PB分别切⊙O于A、B，E为劣弧AB上一点，过E点的切线交P A于C、交PB于D．（1）若P A＝6，求△PCD的周长．（2）若∠P＝50°求∠DOC．22．如图，P A、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，交P A、PB于点E、F，已知P A＝12cm，∠P＝40°①求△PEF的周长；②求∠EOF的度数．23．如图，P A、PB切⊙O于A、B两点，CD切⊙O于点E，分别交P A、PB于点C、D．若P A、PB的长是关于x的一元二次方程x2﹣mx+m﹣1＝0的两个根，求△PCD的周长．24．已知：如图，P A、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O 的切线，交P A、PB于E、F点，已知P A＝12cm，求△PEF的周长．25．已知：如图△ABC中，∠ACB＝90°，以AC为直径的⊙O交AB于D，过D作⊙O的切线交BC于点E，EF⊥AB，垂足为F．（1）求证：DE＝BC；（2）若AC＝6，BC＝8，求S△ACD：S△EDF的值．参考答案一．选择题1．解：∵直线P A、PB、MN分别与⊙O相切于点A、B、C，∴MA＝MC，NC＝NB，∴△PMN的周长＝PM+PN+MC+NC＝PM+MA+PN+NB＝P A+PB＝7.5+7.5＝15（cm）．故选：D．2．解：设⊙O与正方形ABCD的边CD切于E，与BC切于F，连接OE，OF，则四边形OECF是正方形，∴CF＝CE＝OE＝OF，∠OEM＝∠OFN＝∠EOF＝90°，∵∠MON＝90°，∴∠EOM＝∠FON，∴△OEM≌△OFN（ASA），∴EM＝NF，∴CM+CN＝CE+CF＝4，∴OE＝2，∴⊙O的面积为4π，故选：C．3．解：∵四边形ABCD是⊙O的外切四边形，∴AD+BC＝AB+CD＝22，∴四边形ABCD的周长＝AD+BC+AB+CD＝44，故选：A．4．解：∵AC、AP为⊙O的切线，∴AC＝AP＝3，∵BP、BD为⊙O的切线，∴BP＝BD，∴BD＝PB＝AB﹣AP＝5﹣3＝2．故选：C．5．解：∵菱形的边长与它的一边相外切的圆的周长相等∴圆在菱形的边上转了4圈∵圆在菱形的四个顶点处共转了360°，∴圆在菱形的四个顶点处共转1圈∴回到原出发位置时，这个圆共转了5圈．故选：B．6．解：∵⊙O是四边形ABCD的内切圆，∴AF＝AE，BF＝BG，CG＝CH，DH＝DE，∴AB+CD＝AF+BF+CH+DH＝AE+BG+CG+DE＝AD+BC．①AF＝BG；④BG＜CG无法判断．正确的有②③故选：B．二．填空题7．解：∵P A、PB、DE分别切⊙O于A、B、C，∴P A＝PB，DA＝DC，EC＝EB；∴C△PDE＝PD+DE+PE＝PD+DA+EB+PE＝P A+PB＝20；∴P A＝PB＝10，故答案为10．8．解：如图所示：连接圆心与各切点，在Rt△DEO和Rt△DFO中，∴Rt△DEO≌Rt△DFO（HL），∴∠1＝∠2，同理可得：Rt△AFO≌Rt△AMO，Rt△BMO≌Rt△BNO，Rt△CEO≌Rt△CNO，∴∠3＝∠4，∠5＝∠7，∠6＝∠8，∴∠5+∠6＝∠7+∠8＝108°，∴2∠2+2∠3＝360°﹣2×108°，∴∠2+∠3＝∠DOC＝72°．故答案为：72°．9．解：设AB和BC上的切点分别为E、F，连接OA、OE、OB、OF，则OE⊥AB，OF⊥BC，∵⊙O内切于菱形ABCD，∴OE＝OF，∴OB平分∠ABC，∵∠ABC＝60°，∴∠ABO＝30°，同理得∠BAO＝60°，∴∠AOB＝90°，∴AO＝AB＝2，OB＝2，∴S△AOB＝AB•OE＝AO•OB，4OE＝2×，OE＝，故答案为：．10．解：设AE的长为x，正方形ABCD的边长为a，∵CE与半圆O相切于点F，∴AE＝EF，BC＝CF，∵EF+FC+CD+ED＝12，∴AE+ED+CD+BC＝12，∵AD＝CD＝BC＝AB，∴正方形ABCD的边长为4；在Rt△CDE中，ED2+CD2＝CE2，即（4﹣x）2+42＝（4+x）2，解得：x＝1，∵AE+EF+FC+BC+AB＝14，∴直角梯形ABCE周长为14．故答案为：14．11．解：∵P A，PB是⊙O的切线，∴P A＝PB，P A⊥OA，∴∠P AB＝∠PBA，∠OAP＝90°，∴∠PBA＝∠P AB＝90°﹣∠OAB＝90°﹣38°＝52°，∴∠P＝180°﹣52°﹣52°＝76°；故答案为：76．12．解：∵四边形ABCD是⊙O的外切四边形，∴AD+BC＝AB+CD＝22，∴四边形ABCD的周长＝AD+BC+AB+CD＝44，故答案为：44．13．解：分两种情况：①点C在劣弧AB上时，如图，当根据切线长定理得：AD＝CD，BE＝CE，P A＝PB，则△PDE的周长＝PD+DE+PE＝PD+CD+CE+PE＝PD+AD+PE+BE＝P A+PB＝2P A＝20cm．②点C在优弧AB上时，如图，当根据切线长定理得：AD＝CD，BE＝CE，P A＝PB，则△PDE的周长＝PD+DE+PE＝2P A+2DE＝20+2×7＝34cm．综上，△PDE的周长为20或34cm．故答案为：20或34．14．解：∵P A、PB切⊙O于A、B，∴P A＝PB＝15；同理，可得：EC＝CA，DE＝DB；∴△PDC的周长＝PC+CE+DE+DP＝PC+AC+PD+DB＝P A+PB＝2P A＝30．即△PCD的周长是：30．故答案为：30．15．解：∵△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，AD ＝10cm，∴设E、F分别是⊙O的切点，故DM＝MF，FN＝EN，AD＝AE，∴AM+AN+MN＝AD+AE＝10+10＝20（cm）．故答案是：20cm．16．解：∵四边形ABCD是圆的切线．∴AH＝AE，BE＝BF，CF＝CG，DH＝DG∴AH+DH+BF+CF＝AE+BE+CG+DG即：AD+BC＝AB+CD∴四边形的周长是10cm．故答案是：10．三．解答题17．解：根据切线的性质得：∠P AC＝90°，所以∠P AB＝90°﹣∠BAC＝90°﹣20°＝70°，根据切线长定理得P A＝PB，所以∠P AB＝∠PBA＝70°，所以∠P＝180°﹣70°×2＝40°．18．（1）证明：连接OP．∵P A、PC分别与⊙O相切于点A，C，∴P A＝PC，OA⊥P A，∵OA＝OC，OP＝OP，∴△OP A≌△OPC（SSS），∴∠AOP＝∠POC，∵QP⊥P A，∴QP∥BA，∴∠QPO＝∠AOP，∴∠QOP＝∠QPO，∴OQ＝PQ．（2）设OA＝r．∵OB＝OC，∴∠OBC＝∠OCB，∵OB∥QD，∴∠QDC＝∠B，∵∠OCB＝∠QCD，∴∠QCD＝∠QDC，∴QC＝QD＝6，∵QO＝QP，∴OC＝DP＝r，∵PC是⊙O的切线，∴OC⊥PC，∴∠OCP＝∠PCQ＝90°，在Rt△PCQ中，∵PQ2＝PC2+QC2，∴（6+r）2＝62+（2r）2，r＝4或0（舍弃），∴OP＝＝4，∵OB＝PD，OB∥PD，∴四边形OBDP是平行四边形，∴BD＝OP＝4．19．解：（1）∵P A、PB、DE都为⊙O的切线，∴DA＝DF，EB＝EF，P A＝PB＝6，∴DE＝DA+EB，∴PE+PD+DE＝P A+PB＝12，即△PDE的周长为12；（2）连接OF，∵P A、PB、DE分别切⊙O于A、B、F三点，∴OB⊥PB，OA⊥P A，∠BOE＝∠FOE＝∠BOF，∠FOD＝∠AOD＝∠AOF，∵∠APB＝52°，∴∠AOB＝360°﹣90°﹣90°﹣52°＝128°，∴∠DOE＝∠FOE+∠FOD＝（∠BOF+∠AOF）＝∠BOA＝64°．20．解：（1）连接OF；根据切线长定理得：BE＝BF，CF＝CG，∠OBF＝∠OBE，∠OCF ＝∠OCG；∵AB∥CD，∴∠ABC+∠BCD＝180°，∴∠OBE+∠OCF＝90°，∴∠BOC＝90°；（2）由（1）知，∠BOC＝90°．∵OB＝6cm，OC＝8cm，∴由勾股定理得到：BC＝＝10cm，∴BE+CG＝BC＝10cm．（3）∵OF⊥BC，∴OF＝＝4.8cm．21．解：（1）连接OE，∵P A、PB与圆O相切，∴P A＝PB＝6，同理可得：AC＝CE，BD＝DE，△PCD的周长＝PC+PD+CD＝PC+PD+CE+DE＝P A+PB＝12；（2）∵P A PB与圆O相切，∴∠OAP＝∠OBP＝90°∠P＝50°，∴∠AOB＝360°﹣90°﹣90°﹣50°＝130°，在Rt△AOC和Rt△EOC中，，∴Rt△AOC≌Rt△EOC（HL），∴∠AOC＝∠COE，同理：∠DOE＝∠BOD，∴∠COD＝∠AOB＝65°．22．解：①∵P A、PB是⊙O的切线，∴P A＝PB，又∵直线EF是⊙O的切线，∴EB＝EQ，FQ＝F A，∴△PEF的周长＝PE+PF+EF＝PE+PF+EB+F A＝P A+PB＝2P A＝24cm；②连接OE，OF，则OE平分∠BEF，OF平分∠AFE，则∠OEF+∠OFE＝（∠P+∠PFE）+∠（P+∠PEF）＝（180°+40°）＝110°，∴∠EOF＝180°﹣110°＝70°．23．解：∵P A、PB的长是关于x的一元二次方程x2﹣mx+m﹣1＝0的两个根，∴P A+PB＝m，P A•PB＝m﹣1，∵P A、PB切⊙O于A、B两点，∴P A＝PB＝，即•＝m﹣1，即m2﹣4m+4＝0，解得：m＝2，∴P A＝PB＝1，∵P A、PB切⊙O于A、B两点，CD切⊙O于点E，∴AD＝ED，BC＝EC，∴△PCD的周长为：PD+CD+PC＝PD+DE+EC+PC＝PD+AD+BC+PC＝P A+PB＝2．24．解：∵P A、PB是⊙O的切线，切点分别是A、B，∴P A＝PB＝12，∵过Q点作⊙O的切线，交P A、PB于E、F点，∴EB＝EQ，FQ＝F A，∴△PEF的周长是：PE+EF+PF＝PE+EQ+FQ+PF，＝PE+EB+PF+F A＝PB+P A＝12+12＝24，答：△PEF的周长是24．25．（1）证明：∵EC、ED都是⊙O的切线，∴EC＝ED，∠ECD＝∠EDC．∵∠EDC+∠EDB＝90°，∠ECD+∠B＝90°，∴∠EDB＝∠B．∴ED＝BE．∴DE＝BE＝EC．∴DE＝BC．（2）解：在Rt△ABC中，AC＝6，BC＝8，则AB＝10，根据射影定理可得：AD＝AC2÷AB＝3.6，BD＝BC2÷AB＝6.4，∴S△ACD：S△BCD＝AD：BD＝9：16，∵ED＝EB，EF⊥BD，∴S△EDF＝S△EBD，同理可得S△EBD＝S△BCD，∴S△EDF＝S△BCD，∴S△ACD：S△EDF＝．。

27.2.3 切线第2课时切线长定理及三角形的内切圆知|识|目|标1．经历折叠纸片的操作过程，归纳得出切线长定理并掌握切线长定理．2．经历教材中“试一试”的实践操作，理解三角形的内切圆及相关知识．目标一能探索并掌握切线长定理例1 教材补充例题如图27－2－12，已知⊙O的切线PA，PB，A，B为切点，把⊙O沿着直线OP对折，你能发现什么？请证明你所发现的结论．结论：PA＝________，∠OPA＝________.图27－2－12证明：如图27－2－13，连结OA，OB.∵PA，PB与⊙O相切，A，B是切点，∴OA⊥________，OB⊥________，即∠OAP＝________＝90°.∵__________________________，∴Rt△AOP≌Rt△BOP(H.L.)，∴PA＝________，∠OPA＝________．图27－2－13试用文字语言叙述你所发现的结论．例2 高频考题如图27－2－14，PA，PB分别切⊙O于A，B两点，∠OAB＝30°.(1)求∠APB的度数；(2)当OA＝3时，求AP的长．图27－2－14【归纳总结】切线长定理中的基本图形：如图27－2－15，PA，PB为⊙O的切线，A，B为切点，此图形中含有：图27－2－15(1)两个等腰三角形 (△PAB，△OAB)；(2)一条特殊的角平分线( OP平分∠APB和∠AOB);(3)三个垂直关系 (OA⊥PA, OB⊥PB，OP⊥AB)．目标二理解三角形的内切圆例3 教材补充例题如图27－2－16，已知△ABC的内切圆⊙O与各边分别相切于点D，E，F，则点O是△DEF的( )图27－2－16A．三条中线的交点B．三条高的交点C．三条角平分线的交点D．三条边的垂直平分线的交点例4 教材补充例题△ABC的内切圆的半径为r，△ABC的周长为l，求△ABC的面积S.【归纳总结】三角形“四心”的区别：提示：(1)这个顶点处的内角；三角形的内心都在三角形内部．(2)三角形的内切圆有且只有一个，而圆有无数个外切三角形．(3)常用S △ABC ＝12(a ＋b ＋c )r (其中a ，b ，c 为△ABC 的三边长)求三角形的内切圆的半径r .(4)若△ABC 为直角三角形(不妨设∠C ＝90°)，则△ABC 内切圆的半径r ＝a ＋b －c2或r ＝aba ＋b ＋c(其中a ，b ，c 分别为∠A ，∠B ，∠C 的对边)．知识点一 切线长及切线长定理(1)圆的切线上某一点与________之间的线段的长叫做这点到圆的切线长． (2)过圆外一点所画的圆的两条切线，________相等．这一点和圆心的连线平分____________________． 知识点二 三角形的内切圆(1)与三角形________________叫做这个三角形的内切圆，三角形的内切圆的圆心叫做这个三角形的________，这个三角形叫做这个圆的外切三角形．(2)三角形的内心就是三角形______________，三角形的内心到____________的距离相等．如图27－2－17是切线长定理的一个基本图形(PA ，PB 为⊙O 的切线，A ，B 为切点)，由切线长定理可以推出很多的结论，如：(1)垂直：OA ⊥________，OB ⊥________，AB ⊥________；(2)角相等：∠1＝∠________＝∠________＝∠________，∠5＝∠________＝∠________＝∠________；(3)线段相等：PA ＝________，AC ＝________； (4)弧相等：AD ︵＝________，AE ︵＝________．图27－2－17教师详解详析【目标突破】 例1 解：PB ∠OPB PA PB ∠OBP OA ＝OB ，OP ＝OP PB ∠OPB 用文字语言叙述结论：过圆外一点所画的圆的两条切线，它们的切线长相等．这一点和圆心的连线平分这两条切线的夹角． 例2 [解析] (1)方法一：根据切线的性质可知：∠OAP ＝∠OBP ＝90°.根据三角形的内角和为180°可求出∠AOB 的度数，再根据四边形的内角和为360°可求出∠APB 的度数；方法二：证明△ABP 为等边三角形，从而可求出∠APB 的度数．(2)方法一：作辅助线，连结OP.在Rt △OAP 中，利用三角函数可求出AP 的长；方法二：作辅助线，过点O 作OD ⊥AB 于点D.在Rt △OAD 中，求出AD 的长，从而求出AB 的长，即为AP 的长．解：(1)方法一：∵在△ABO 中，OA ＝OB ，∠OAB ＝30°， ∴∠AOB ＝180°－2×30°＝120°. ∵PA ，PB 是⊙O 的切线， ∴OA ⊥PA ，OB ⊥PB ， ∴∠OAP ＝∠OBP ＝90°， ∴在四边形OAPB 中，∠APB ＝360°－120°－90°－90°＝60°. 方法二：∵PA ，PB 是⊙O 的切线， ∴PA ＝PB ，OA ⊥PA. ∵∠OAB ＝30°，∴∠BAP ＝90°－30°＝60°， ∴△ABP 是等边三角形， ∴∠APB ＝60°.(2)方法一：如图①，连结OP. ∵PA ，PB 是⊙O 的切线， ∴PO 平分∠APB ， 即∠APO ＝12∠APB ＝30°.又∵在Rt △OAP 中，OA ＝3， ∴AP ＝OAtan 30°＝3 3.方法二：如图②，过点O 作OD ⊥AB 于点D. ∵在△OAB 中，OA ＝OB ， ∴AD ＝12AB.∵在Rt △AOD 中，OA ＝3，∠OAD ＝30°，∴AD ＝OA ·cos 30°＝3 32，∴AB ＝2AD ＝3 3， ∴AP ＝AB ＝3 3. 例3 [答案] D例4 解：如图，设△ABC 的内切圆⊙O 与三边分别相切于点D ，E ，F ，连结OA ，OB ，OC ，OD ，OE ，OF ，则OD ⊥AB ，OE ⊥BC ，OF ⊥AC.所以S ＝S △AOB ＋S △AOC ＋S △BOC ＝12AB ·OD ＋12AC ·OF ＋12BC ·OE ＝12lr.【总结反思】[小结] 知识点一 (1)切点(2)它们的切线长 这两条切线的夹角 知识点二 (1)各边都相切的圆 内心 (2)三条角平分线的交点 三角形三边[反思] (1)PA PB PO (2)2 3 4 6 7 8 (3)PB BC (4)BD ︵ BE ︵。

类型一：切线的证明考点一：通过证明三角形全等得出垂直如图，Rt△ABC中，∠A=90°，以AB为直径的⊙O交BC于点D，点E在⊙O 上，CE=CA，AB，CE的延长线交于点F.连接OE、OC，通过“ SSS”证明△AOC≌△EOC，从而推出∠CEO=90°，进而证明CF为⊙O的切线【经典例题1】如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD＝，AC＝8，求图中阴影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．【解析】证明：⑴如图，连接OC，∵PA切⊙O于A．∴∠PAO=90º．∵OP∥BC，∴∠AOP=∠OBC，∠COP=∠OCB．∵OC=OB，∴∠OBC=∠OCB，∴∠AOP=∠COP．又∵OA=OC，OP=OP，∴△PAO≌△PCO (SAS)．又∵OC 是⊙O 的半径，∴PC 是⊙O 的切线．⑵解法一：由（1）得PA ，PC 都为圆的切线，∴PA=PC ，OP 平分∠APC ，∠ADO=∠PAO=90 º，∴∠PAD+∠DAO=∠DAO+∠AOD ，∴∠PAD =∠AOD ，∴△ADO ∽△PDA ．∴AD/PD=DO/AD ，∴AD 2=PD*DO ，∵AC=8， PD=316， ∴AD=21AC=4，OD=3，AO=5， 由题意知OD 为△ABC 的中位线，∴BC=2OD=6，AB=10．∴S 阴=S 半⊙O －S △ACB=24825-π． 答：阴影部分的面积为24825-π． 解法二：∵AB 是⊙O 的直径，OP ∥BC ，∴∠PDC=∠ACB=90º．∵∠PCO=90 º，∴∠PCD+∠ACO=∠ACO+∠OCB=90 º，即∠PCD=∠OCB ．∴∠PCD=∠OBC ，∴△PDC ∽△ACB ， ∴PD/AC=DC/CB=PC/AB ．又∵AC=8， PD=316， ∴AD=DC=4，PC=320． ∴AB CB 32048316==， ∴CB=6，AB=10，∴S 阴=S 半⊙O-S △ACB=24825-π． 答：阴影部分的面积为24825-π． （3）如图，连接AE ，BE ，过点B 作BM ⊥CE 于点M ．∴∠CMB=∠EMB=∠AEB=90º，又∵点E 是AB 的中点，∴∠ECB=∠CBM=∠ABE=45º，CM=MB =23，BE=ABcos45º=25， ∴ EM=24，∴CE=CM+EM=27．答：CE 的长为27cm ．练习1-1如图，以Rt ABC ∆的直角边AC 为直径作⊙O 交斜边AB 于点E ，连接EO 并延长交BC 的延长线于点D ，作// OF AB 交BC 于点F ，连接.EF EC 、(1)求证:OF ⊥CE ；(2)求证:EF 是⊙O 的切线;(3)若⊙O 的半径为3，∠EAC=60°，求tan ∠ADE 的值.【解析】证明：（1）如图1，连接FO，∵F为BC的中点，AO=CO，∴OF∥AB，∵AC是O的直径，∴CE⊥AE，∵OF∥AB，∴OF⊥CE，∴OF所在直线垂直平分CE，∴FC=FE，OE=OC，∴∠FEC=∠FCE，∠0EC=∠0CE，∵∠ACB=90°，即：∠0CE+∠FCE=90°，∴∠0EC+∠FEC=90°，即：∠FEO=90°，∴FE为O的切线；（2）如图2，∵ O的半径为3，∴AO=CO=EO=3，∵∠EAC=60°，OA=OE，∴∠EOA=60°，∴∠COD=∠EOA=60°，∵在Rt△OCD中，∠COD=60°，OC=3，∴CD=23，∵在Rt△ACD中，∠ACD=90°，CD=23，AC=4，∴AD=27考点二：通过平行（垂直，互余等）如图，AB是⊙O的直径，C，D是⊙O上两点，且弧BC=弧CD，过点C的直线CF⊥AD于点F，交AB的延长线于点E，连接AC．连接OC，由弧BC=弧CD，OA=OC，∠CAD=∠CAB=∠OCA，推出OC∥AF，∠OCF=90°，进而证明EF为⊙PO的切线.26. (2019•襄阳)如图，点E是ABC△的外接圆圆△的内心，AE的延长线和ABC∥．O相交于点D，过D作直线DG BC(1)求证：DG是圆O的切线；(2)若6DE=，63BC=，求优弧BAC的长．【解析】(1)连接OD交BC于H，如图，∵点E是ABC△的内心，∠=∠，∴AD平分BAC∠，即BAD CAD=，∴BD CD=，∴OD BC，BH CH∥，∵DG BC⊥，∴OD DG∴DG 是圆O 的切线．(2)连接BD 、OB ，如图，∵点E 是ABC △的内心，∴ABE CBE ∠=∠，∵DBC BAD ∠=∠，∴DEB BAD ABE DBC CBE DBE ∠=∠+∠=∠+∠=∠，∴6DB DE ==， ∵1332BH BC ==， 在Rt BDH △中，333sin 62BH BDH BD ∠===， ∴60BDH ∠=︒，而OB OD =，∴OBD △为等边三角形，∴60BOD ∠=︒，6OB BD ==，∴120BOC ∠=︒，∴优弧BAC 的长=(360120)π68π180-⋅⋅=．如图， AB 是⊙O 的直径，C 为⊙O 上一点，经过点C 的直线与AB 的延长线交于点D ，连接AC ，BC ，∠BCD=∠CAB ，E 是⊙O 上一点，弧CE=弧CB ，连接AE 并延长与DC 的延长线交于点F ．求证：(1)DC 是⊙O 的切线． (2)若⊙O 的半径为3，sinD=53，求线段AF 的长．【经典例题2】如图，M ，N 是以AB 为直径的⊙O 上的点，且弧AN=弧BN ，弦MN 交AB 于点C ，BM 平分∠ABD ，MF ⊥BD 于点F ，（1）求证：MF 是⊙O 的切线；（2）若CN=3，BN=4，求CM 的长.【解析】如图，圆O 是ABC △的外接圆，AE 平分BAC ∠交圆O 于点E ，交BC 于点D ，过点E 作直线l BC ∥．（1）判断直线l 与圆O 的关系，并说明理由；（2）若ABC ∠的平分线BF 交AD 于点F ，求证：BE EF =；（3）在（2）的条件下，若5DE =，3DF =，求AF 的长．【解析】（1）直线l 与⊙O 相切．理由：如图1所示：连接OE 、OB 、OC ．∵AE 平分∠BAC ，∴∠BAE=∠CAE ．∴弧BE=弧CE ．∴∠BOE=∠COE ．又∵OB=OC ，∴OE ⊥BC ．∵l ∥BC ，∴OE ⊥l ．∴直线l 与⊙O 相切．（2）∵BF 平分∠ABC ，∴∠ABF=∠CBF ．又∵∠CBE=∠CAE=∠BAE ，∴∠CBE+∠CBF=∠BAE+∠ABF ．又∵∠EFB=∠BAE+∠ABF ，∴∠EBF=∠EFB ．∴BE=EF ．（3）由（2）得BE=EF=DE+DF=7．∵∠DBE=∠BAE ，∠DEB=∠BEA ，∴△BED ∽△AEB ．∴DE/BE=BE/AE ，即4/7=7/AE ，解得；AE=449． ∴AF=AE ﹣EF=449﹣7=421．(2017·营口)如图，点E 在以AB 为直径的⊙O 上，点C 是BE ︵的中点，过点C 作CD ⊥AE ，交AE 的延长线于点D ，连接BE 交AC 于点F.(1)求证：CD 是⊙O 的切线；(2)若cos ∠CAD ＝45，BF ＝15，求AC 的长．4．(2018·咸宁)如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC交BC的延长线于点E.(1)求证：DE是⊙O的切线；(2)若AB＝25，BC＝5，求DE的长．【解析】5．(2019·原创)如图，在△ABC中，CA＝CB，∠CAB＝30°，⊙O经过点C，且直径AD在线段AB上，连接OC，OE平分∠AOC交弧AC于点E，连接AE，EC.(1)求证：CB是⊙O的切线；(2)若M在边AC上，OM＝CM＝2，求△ABC的面积．6．(2018·成都)如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G.(1)求证：BC是⊙O的切线；(2)设AB＝x，AF＝y，试用x，y的代数式表示线段AD的长；(3)若BE＝8，sin B＝513，求DG的长．通过等腰三角形倒角证明切线已知：如图，在△ABC中，AC=BC，以AC为直径的⊙O交于点D，DE⊥BC．连接OD，由，AC=BC，OA=OD，推出∠A=∠B=∠ODA，推出OD∥BC，∠ODE=90°，进而证明为⊙的切线.如图，已知△ABC是等边三角形，以AB为直径作⊙O，交BC边于点D，交AC边于点F，作DE⊥AC于点E．求证：(1)DE是⊙O的切线．(1)若△ABC的边长为4，求EF的长度．通过弦切角定理证明切线如图，AB是⊙O的直径，点E是弧BD上一点，∠DAC=∠AED.由∠DAC=∠AED=∠ABD，推出∠BAC=90°，进而证明AC为⊙O的切线.补充弦切角定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．已知：⊙O是△ABC的外接圆，过点B作⊙O的切线MN.∠ABM、∠CBN即为弦切角．弦切角定理：弦切角的度数等于它所夹的弧所对的圆心角度数的一半，等于它所夹的弧所对的圆周角度数．即有∠ABM=∠ACB，∠CBN=∠BAC.【证明】连接BO并延长交⊙O于D，连接AD、CD、∵ BD是直径，∴∠BAD=∠BCD=90°.又∵∠BDC+∠DBC=90°，∠CBN+∠DBC=90°，∴∠CBN=∠BDC．同理可证：∠ABM=∠ADB.如图，AB为⊙O的直径，点D，E为⊙O上的两个点，延长AD至C，使∠CBD=∠BED．求证：(1)BC是⊙O的切线．(2)当点E为弧AD的中点且∠BED=30°时，⊙O半径为2，求DF的长度．【解析】（1）证明：∵AB为⊙O的直径，∴∠ADB=90°，∴∠A+∠DBA=90°，∵弧BD=弧BD，∴∠A=∠E，∵∠CBD=∠E，∴∠CBD=∠A，∴∠CBD+∠DBA=90°，∴AB⊥BC，∴BC 是⊙O 的切线，（2） ∵∠BED=30°，∴∠A=∠E=∠CBD=30°，∴∠DBA=60°，∵点E 为弧AD 的中点，∴∠EBD=∠EBA=30°，∵⊙O 半径为2，∴AB=4，BD=2，AD=23， 在Rt △BDF 中，∠DBF=90°，tan ∠DBF=DF/BD=33， ∴DF=332．如图，AB 为⊙O 的直径，C 为⊙O 上一点，过点C 作⊙O 的切线，交BA 的延长线交于点D ，过点B 作BE ⊥BA ，交DC 延长线于点E ，连接OE ，交⊙O 于点F ，交BC 于点H ，连接AC ．（1）求证：∠ECB=∠EBC ；（2）连接BF ，CF ，若CF=6，sin ∠FCB=53，求AC 的长．【解析】（1）证明：∵BE ⊥OB ，∴BE 是⊙O 的切线，∵EC 是⊙O 的切线，∴EC=EB ，∴∠ECB=∠EBC ．（2） 连接CF 、CO 、AC ．∵EB=EC ，OC=OB ，∴EO ⊥BC ，∴∠CHF=∠CHO=90°，在Rt △CFH 中，∵CF=6，sin ∠FCH=53， ∴FH=CF •sin ∠FCH=518，CH=52422=-FH CF ， 设OC=OF=x ，在Rt △COH 中，∵OC 2=CH 2+OH 2，∴x 2=（524）2+（x -518）2， ∴x =5，∴OH=57， ∵OH ⊥BC ，∴CH=HB ，∵OA=OB ，∴AC=2OH=514．4．(2018·兰州)如图，AB 为圆O 的直径，C 为圆O 上的一点，D 为BA 延长线上的一点，∠ACD ＝∠B.(1)求证：DC 为圆O 的切线；(2)线段DF 分别交AC ，BC 于点E ，F ，且∠CEF ＝45°，圆O 的半径为5，sin B ＝35，求CF 的长．如图，四边形ABCD 中，AB=AD=CD ，以AB 为直径的⊙O 经过点C ，连接AC 、OD 交于点E.(1)证明：OD ∥BC ；(2)若tan ∠ABC=2，证明：DA 与⊙O 相切；(3)在(2)条件下，连接BD 交⊙O 于点F ，连接EF ，若BC=1，求EF 的长。

知识点一、切线长定理1如图，一把直尺，60°的直角三角板和光盘如图摆放，A为60°角与直尺交点，AB=3，则光盘的直径是（）A．3 B．C．6 D．2. 如图，AB是⊙O 的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．（1）求证：OP⊥CD；（2）连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．3.如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．（1）求证：DA=DE；（2）若AB=6，CD=4，求图中阴影部分的面积．知识点二、正多边形和圆1.若正六边形的内切圆半径为2，则其外接圆半径为____________．2.如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，则∠BDF的度数是.知识点三、弧长和扇形面积1.如图，△ABC内接于⊙O，若∠A=45°，⊙O的半径r=4，则阴影部分的面积为( )A.4π-8B. 2πC.4πD. 8π-82. 若扇形的圆心角为90°，半径为6，则该扇形的弧长为（）A．32B．2πC．3πD．6π3.一个扇形的圆心角为135°，弧长为3πcm，则此扇形的面积是4.一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B 点从开始至结束所走过的路径长度为（ ）A ．B ．C ．4D ．2+5 如图,在Rt △ABC 中,∠ABC ＝90°,AB ＝＝2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )A.2πB.2πC.πD.2π6. 如图，在△AOC 中，OA =3cm ，OC =lcm ，将△AOC 绕点D 顺时针旋转90 °后得到△BOD ，则AC 边在旋转过程中所扫过的图形的面积为( )cm 2 A ．2πB ．2π C.178πD ．198π7.如图，分别以等边三角形ABC 的三个顶点为圆心，以边长为半径画弧，得到的封闭图形是莱洛三角形，若AB=2，则莱洛三角形的面积（即阴影部分面积）为（ ） A ．B ．C ．2D ．2知识点四、圆锥的侧面积1.已知一个圆锥的底面半径为3cm ，母线长为10cm ，则这个圆锥的侧面积为（ ）A ．30πcm 2B ．50πcm 2C ．60πcm 2D ．3πcm 22.用一块圆心角为216°的扇形铁皮，做一个高为40cm 的圆锥形工件（接缝忽略不计），那么这个扇形铁皮的半径是 cm ．3..如图是一个圆锥的主视图,根据图中标出的数据(单位：cm),计算这个圆锥侧面展开图圆心角的度数为________.4.如图，点O 为正六边形ABCDEF 的中心，点M 为AF 中点，以点O 为圆心，以OM 的长为半径画弧得到扇形MON ，点N 在BC 上；以点E 为圆心，以DE 的长为半径画弧得到扇形DEF ，把扇形MON 的两条半径OM ，ON 重合，围成圆锥，将此圆锥的底面半径记为r 1；将扇形DEF 以同样方法围成的圆锥的底面半径记为r 2，则r 1：r 2= ．知识点五、切线的性质和判定巩固练习1. 如图，已知三角形ABC 的边AB 是⊙O 的切线，切点为B ．AC 经过圆心O 并与圆相交于点D 、C ，过C 作直线CE 丄AB ，交AB 的延长线于点E ． （1）求证：CB 平分∠ACE ；（2）若BE=3，CE=4，求⊙O 的半径．2.如图，AB是⊙O的直径，点D在⊙O上（点D不与A，B重合），直线AD交过点B的切线于点C，过点D作⊙O的切线DE交BC于点E．（1）求证：BE=CE；（2）若DE∥AB，求sin∠ACO的值．3.已知：如图，AB、AC是⊙O的两条弦，且AB＝AC，D是AO延长线上一点，联结BD并延长交⊙O于点E，联结CD并延长交⊙O于点F．（1）求证：BD＝CD；（2）如果AB2＝AO•AD，求证：四边形ABDC是菱形．。