分解质因数练习题10道

分解质因数一填空1、一个数（），这样的数叫做质数．2、一个数（），这样的数叫做合数．3、20以内的质数有（）．4、把一个合数（），叫做分解质因数．5、一个数既是18的约数，又是18的倍数，把它写成两个质数相加的形式是（）或（）．6、最小的合数是（），最小的质数是（），既是偶数又是质数的数（），既是奇数又是合数的数最小是（）．7、10以内所有质数的积减去最小的三位数，差是（）．8、20以内差为1的两个合数有（）和（），（）和（），（）和（），（）和（）四对．9、一个两位数的质数，它个位上的数与十位上的数交换位置后，仍是一个质数．这样的数有（）．10、把下面两个数写成几个质数和的形式：15＝（）＋（） 20＝（）＋（）＝（）＋（）二、判断1、自然数不是质数就是合数．（）2、所有的质数都是奇数，所有的合数都是偶数．（）3、把24分解质因数可以写成24＝1×2×2×2×3．（）4、两个数的全部质因数相同，这两个数一定相同．（）5、只有两个约数的数，一定是质数．（）6、质数只有两个约数．（）7、两个自然数的和一定是合数，两个质数的和一定是偶数．（）8、2和5都是质因数．（）9、1是自然数，但它不是质数，也不是合数．（）10、合数只有3个约数．（）三、选择题．1、把36分解质因数可以写成（）．①36＝4×9 ②36＝1×2×3×2×3 ③36＝2×3×2×32、因为210＝2×3×5×7，所以说（）．①210有四个不同的约数②210有四个不同的质数③210有四个不同的质因数3、下面各式中属于分解质因数的是（）①42＝2×3×7 ②12＝3×4 ③54＝2×3×3×3×1 ④2×2×5＝204、最小的质数乘最小的合数，积是（）．①4 ②6 ③8 ④105、自然数按约数的个数分，可以分为（）．①质数和合数②奇数和偶数③质数、合数和0 ④质数、合数和16、质数与质数的积是（）①合数②质数③可能是质数、可能是合数．7、9和7叫63的（）①因数②质因数③质数8、37×（）的积是质数①1 ②可以是1，也可以是别的数③质数四解决问题1、食品店运来75个面包，如果每2个装一袋，能正好装完吗？如果每5个装一袋，能正好装完吗？如果每3个装一袋，能正好装完吗？为什么？2、晚上小明家正开着灯在吃晚饭，顽皮的弟弟按了5下开关，这时灯是亮还是暗？如果按了50下呢？3、幼儿园里有一些小朋友，王老师拿了32颗糖平均分给他们，正好分完。

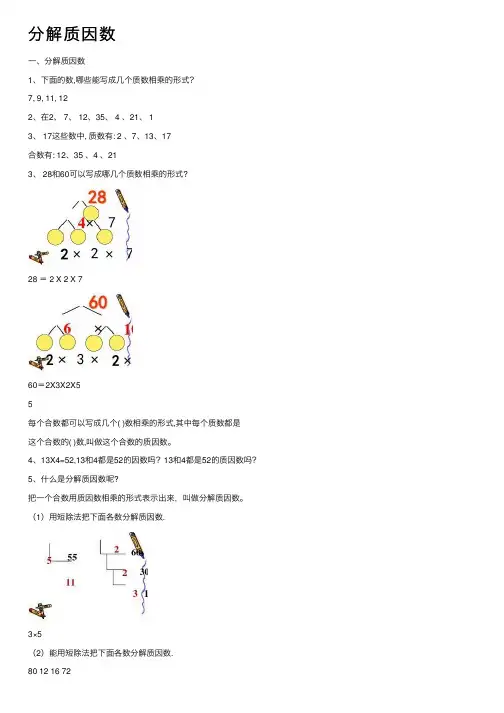
分解质因数⼀、分解质因数1、下⾯的数,哪些能写成⼏个质数相乘的形式？7, 9, 11, 122、在2、 7、 12、35、 4 、21、 13、 17这些数中, 质数有: 2 、7、13、17合数有: 12、35 、4 、213、 28和60可以写成哪⼏个质数相乘的形式?28 ＝ 2 X 2 X 760＝2X3X2X55每个合数都可以写成⼏个( )数相乘的形式,其中每个质数都是这个合数的( )数,叫做这个合数的质因数。

4、13X4=52,13和4都是52的因数吗？13和4都是52的质因数吗？5、什么是分解质因数呢?把⼀个合数⽤质因数相乘的形式表⽰出来，叫做分解质因数。

（1）⽤短除法把下⾯各数分解质因数.3×5（2）能⽤短除法把下⾯各数分解质因数.80 12 16 72练习：⼀、选⼀选。

(1)把10分解质因数是( )A.10=2×5B.10=1×2×5C.10=1×10(2)把27分解质因数是( )A.3×9=27B.3×3×3=27C.27=3×3×3（2）看谁是⼩判官①把35分解质因数是 35=1×5×7（）②把49分解质因数是7×7=49 ( )③把30分解质因数是30=2×3×5 ( )④51不能分解质因数. ( )⼆、⽤短除法找最⼤公因数1．⽤排列因数的⽅法求18和24的最⼤公因数。

2．⽤排列因数的⽅法求两个数的最⼤公约数⽅便吗？有没有⽐它简便的⽅法求最⼤公约数呢？今天我们就来研究求两个数的最⼤公因数简便⽅法。

．把18和24分解质因数。

如下：2 1 8 2 2 43 9 2 1 23 2 6318＝2×3×324＝2×2×2×3⑴18有哪⼏个质因数？24呢？⑵18和24相同的质因数有哪些？⑶它们相同的质因数叫做什么，给它们起⼀个名字：公有的质因数⑷18和24公有的质因数有哪⼏个？其它的2、2和3是公有的质因数吗？那这些质因数叫做什么质因数，给它们起⼀个名字：独有的质因数⑸你能根据18和24公有的质因数2和3计算出18和24所有的公因数吗？⑹怎么计算的？哪个最⼤？最⼤的是怎么计算出来的？⑺如果在2×3的后⾯再乘以⼀个质因数3，还是公约数吗？是最⼤公约数吗？多乘⼏个质因数呢？⑻如果在2×3的后⾯少乘以⼀个质因数3，还是公约数吗？是最⼤的公约数吗？⑼从这⾥可以看出：两个数的最⼤公因数是什么质因数的乘积？板书：所有的公有质因数的乘积＝最⼤公约数⑽“所有的公有质因数”是什么意思？你是怎么理解的？⑾从这⾥可以看出：⽤分解质因数的⽅法求两个数的最⼤公约数先⼲什么？然后⼲什么？最后⼲什么？18和24的最⼤公约数是：2×3＝6。

□□×□□=1288
例6、三个质数的和是80，这三个数的积最大可以是多少？
巩固、如果A＋B=70，A×B＝1161，那么A－B等于多少？
巩固、把1、2、3、4、5、6、7、8、9九张卡片分给甲、乙、丙三人，每人各3张。甲说：“我的三个数的积是48。”乙说：“我的三个数的和是16。”丙说：“我的三个数的积是63。”问甲、乙、丙各拿了哪几张卡片？
例7、一个两位数除310余37，这个数可以是（ ）或（ ）。
巩固、237除以一个两位数，所得的余数是6，请写出适合于这个条件的所有两位数。
巩固、5100除以一个三位数，余数是95，这个三位数最大是多少？
例8、小明用60元买了一种画片若干张，如果每张画片的价钱便宜1元钱，那么他还能多买3张。问小明买了多少张画片？
例1、把18个苹果平均分成若干份，每份大于1个，小于18个。一共有多少种不同的分法？
巩固、有60个同学分成人数相等的小组去慰问解放军叔叔，每组不少于6人，不多于15人，有哪几种分法？
巩固、195个同学排成长方形队伍做早操，行数和列数都大于1，共有几种排法？
例2、写出若干个连续的自然数，使它的积是15120。
巩固、有三个连续的自然数，乘积是39270立方厘米，求这个三个数的和。
巩固、有4个孩子，恰好一个比一个大1岁，4人的年龄积是3024，问这4个孩子中最大的几岁？
例3、将下面八个数平均分成两组，使这两组数的乘积相等。
2、5、14、24、27、55、56、99
巩固、有三个自然数a、b、c,已知a×b=30,b×c=35,c×a=42,求a×b×c的积是多少？
教学内容
分解质因数
教学目标
掌握分解质因数相关题型
重点
分解质因数
难点

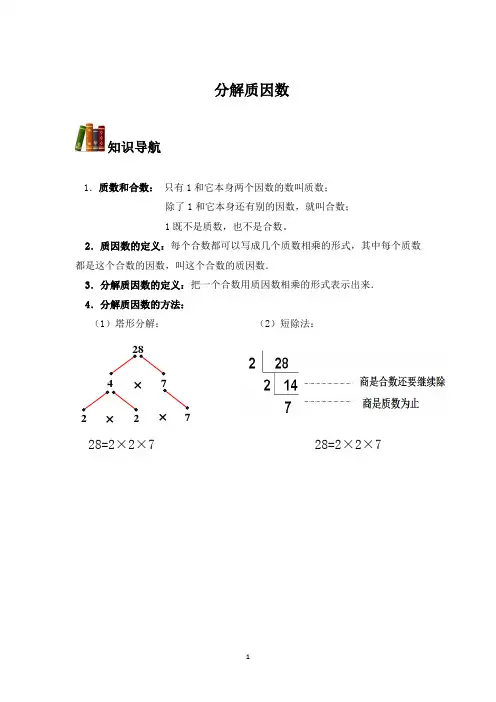
分解质因数知识导航1．质数和合数： 只有1和它本身两个因数的数叫质数；除了1和它本身还有别的因数，就叫合数； 1既不是质数，也不是合数。

2．质因数的定义：每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数，叫这个合数的质因数．3．分解质因数的定义：把一个合数用质因数相乘的形式表示出来． 4．分解质因数的方法：（1）塔形分解： （2）短除法：28=2×2×7 28=2×2×7×××7227428例题分析【理解一】质数和合数.1.找出1-20各数的因数，看看有什么规律：2.质数：只有1和它本身两个因数的数。

3.合数：除了1和它本身还有别的因数的数。

4.在自然数里，1既不是质数也不是合数。

5.找出100以内的质数，做一个质数表。

例1．在括号里填上适当的质数。

18=（）＋（）＋（）24=（）＋（）=（）＋（）=（）＋（）例2．A、B、C是三个不同的质数，且A-B=C，若得数最小，请写出一组符合要求的数：A=（）、B=（）、C=（）。

例3．一个四位数，千位上是最小的质数，百位上是最小的合数，十位上既不是质数也不是合数，个位上是10以内最大的质数，这个数是多少？例4.两个质数的和是 40，这两个质数分别是多少？它们的乘积最大是多少？巩固练习1．一个长方形的边长是以厘米为单位的质数，那么周长是以厘米为单位的（）．A．质数B．合数C．无法确定2．如果两个不同的质数相加还得到质数，其中一个质数必定是（）。

3.在括号里填上适当的数．①11与（）的积是合数②97与（）的积是质数③23与（）的积是偶数④17与（）的积能被3整除⑤13与（）的积能被5整除⑥29与（）的积能被2、3整除⑦37与（）的积能被3、5整除⑧41与（）的积能被2、3、5整除4．当a分别是1、2、3、4、5时，6a＋1是质数，还是合数?5．20以内的质数a和b的和是5的倍数，且a比b小4，这两个质数分别是多少？6.两个质数和为18，积是65，这两个质数是多少？【理解二】质因数和分解质因数．1.分解质因数：把一个合数用质因数相乘的形式表示出来。

分解质因数练习题10道一、填空1、在自然数中，既不是质数也不是合数，在偶数中，是质数．2、在自然数中，既是奇数又是质数的最小的数是，既是一位数奇数又是合数，既是偶数又是质数，既不是质数又不是合数．一个合数至少有个约数．3、用三个一位质数组成能同时被3和5整除的三位数，其中最大的是，最小的数是．、10～20之间的质数有，其中个位上的数字与十位上的数字交换位置后，仍是一个质数．、在1、2、4、10、11这几个数中，是整数，是奇数，是偶数，是质数，是合数．6、20以内差为4的两个质数是和，和，和．7、用最小的质数，最小的奇数，最小的合数和0组成一个四位数，其中能够被2和5同时整除的最大四位数是，只能被2整除的最小四位数是．8、28的约数有，这些数中，质数有，合数有，奇数有，偶数有．9、把下面各数分别填在指定的圈里．9、23、31、39、41、51、69、79、81、89、91、97二、判断1、能被2整除的数都不是质数．、在自然中，除2以外，所有的偶数都是合数．、边长是质数的正方形，它的周长一定是合数．4、只有两个约数的自然数一定是质数．5、自然数中只有质数和合数．、自然数中除了质数、合数，还有1．7.所有的质数都是奇数．8、有三个或三个以上约数的数一定是合数．9、合数有约数，质数没有约数． 10、两个质数的乘积一定是合数． 11.所有合数都是偶数． 12、除了2和5这两个数以外，个位上是0、2、4、6、8、5的数都是合数．三、按要求写数．1、一个四位数，个位上的数既不是质数也不是合数，十位上的数既是质数又是偶数，百位上的数是最小的合数，千位上的数既是奇数又是合数，这个四位数是、能同时被3、5整除的最小的三位数是3、两个质数和为18，积是65，这两个质数是和．4.用10以内的质数组成一个三位数，使它能同时被3、5整除，这个数最小是，最大是。

5.在括号里填上适当的质数①8=＋②12=＋＋③15=＋④18=＋＋⑤24=＋=＋=＋6.两个质数的和是18，积是65，这两个质数分别是多少？7.当a分别是1、2、3、4、5时，6a＋1是质数，还是合数？8.分解质因数。

一、选择题1. 下面分解质因数正确的是（）。

A．18＝3×6 B．30＝2×3×5 C．20＝2×2×5×12. 下面各式中，分解质因数的是（）。

A．B．15＝2＋13 C．18＝3×6 D．3. 6的质因数是（）。

A．6 B．3 C．2 D．2和34. 把12分解质因数，下列选项正确的是（）。

A．＝12 B．C．D．5. 下列各组分数，分母的最小公倍数是24的是（）。

A．和B．和C．和D．和二、填空题6. 两个不同的质数，它们的乘积是14，它们的和是( )。

7. A和B都是自然数，分解质因数A＝2×5×C；B＝3×5×C。

如果A和B的最小公倍数是60，那么C＝________。

8. 分解质因数。

84＝________×________×________×________。

（从小到大依次填写）9. 有两个小朋友，他们的年龄正好是两个连续的自然数，且他们年龄的积是56岁，这两个小朋友的年龄分别是( )岁、( )岁。

10. 两个数的最大公因数是8，最小公倍数是48。

这两个数可能是( )和( )，也可能是( )和( )。

三、解答题11. 一个长方体的长、宽、高是连续的3个自然数，它的体积是39270立方厘米，那么这个长方体的表面积是多少平方厘米？12. 三个连续自然数的乘积是210，求这三个数。

13. 圈出下面数中的合数，再把圈出的合数分解质因数。

11 12 24 19 2817 29 45 87 3114. 有两根绳子，长度分别是27米和45米，要把它们截成同样长的小段，没有剩余，每小段绳子最长是多少米？一共可以截成多少小段？。

分解质因数练习一、填空。

1、把一合数用几个（）的形式表示出来，叫做（）。

2、84的质因数有（）。

3、有三个小朋友，他们的年龄正好是三个连续的自然数，且他们年龄的积是210，这三个小朋友的年龄分别是（）岁、（）岁、（）岁。

4、A、B、C是三个不同的质数，且A-B=C，若得数最小，那么A=（）B=（）C=（）3、26、 1.1这几个数中，自然数有（），5、在0、3、140、17、11偶数有（），奇数有（），质数有（），合数有（）。

6、48的因数有（），它的质因数有（）。

7、最小的质数是（），在一位数中，既不是奇数又不是合数的数是（）。

8、只有（）的数，叫质数，也叫（）数。

9、分解质因数的方法有：（）分解质因数，用（）法分解质因数。

10、非0自然数按因数的个数可以分为（）、（）和（）三类。

11、一个质数，它的最大的因数就是（）。

12、一个正方形的边长是质数，它的周长一定是（）数。

二、判断题。

(对的在括号里画“√”,错的画“×”)1、一个数的因数一定比这个数的倍数小。

（）2、因为2.4÷0.6=4,所以0.6是2.4的倍数。

（）3、一个数的最小倍数与最大因数都是26，这个数一定是26.（）4、只要两个整数相除没有余数（0除外），就说被除数是除数的倍数。

（）三、用短除法分解质因数。

48 51 1321110 129 91分解质因数练习（答案）一、填空。

1、把一合数用几个（质数）的形式表示出来，叫做（分解质因数）。

2、84的质因数有（2、3、7 ）。

3、有三个小朋友，他们的年龄正好是三个连续的自然数，且他们年龄的积是210，这三个小朋友的年龄分别是（5）岁、（6）岁、（7）岁。

4、A、B、C是三个不同的质数，且A-B=C，若得数最小，那么A=（5）B=（3）C=（ 2 ）753、26、 1.1、15这几个数中，自然数有（0、3、140、5、在0、3、140、17、1117、26、15 ），偶数有（0、140、26），奇数有（3、17、15），质数有（3、17），合数有（140、26、15 ）。

8 16 5472
答案
一、1.把一个数写成几个质数相乘的形式2.质数相乘3.短除
4. 2 3
二、1. A 2. B 3. B 4. C
三、3 5 3×5 21 3 7 2×3×7 4 6 2 2 2 3 2×2×2×3
四、8=2×2×2 16=2×2×2×2 54=2×3×3×3 72=2×2×2×3×3
2、在算式20=4×5中，4和5都是20的（）。
A、质因数B、因数C、倍数
3、3和7都是21的（）。
A、质数B、质因数C、倍数
4、一个合数，至少有（）个因数。
A、1B、2C、3
三、把下面各数分解质因数。
15 42 24
（）×（）2×（）（）×（）
15=（）×（）（）×（）（）×（）
42=24=
四、用短除法把下面各数分解质因数。
把282828分解质因数的是分解质因数的是分解质因数的是28228228பைடு நூலகம்728728728281281281222在算式在算式在算式204204204和和和55都是都是都是202020aaa质因数质因数质因数bbb因数因数因数ccc倍数倍数倍数和和和77都是都是都是212121aaa质数质数质数bbb质因数质因数质因数ccc倍数倍数倍数444一个合数至少有一个合数至少有一个合数至少有个因数
5.5分解质因数
一、我会填。
四年级数学上册分解质因数练习题及答案
2、每个合数都可以写成几个（）的形式。
3、把一个合数分解质因数，为了简便，通常用（）法。
4、两个数都是质数的连续自然数是（）和（）。
二、我会选。
1、把28分解质因数的是（）。
A、28=2×2×7B、2×2×7=28C、28=1×2×2×7

小学数学分解质因数分解质因数是小学数学中的重要知识点，它能帮助学生了解一个数的因数及其素因数。

这里给出一份关于小学数学分解质因数的练习题，请同学们认真阅读题目，并用最合适的方法来解答。

每个问题都有配套的解析，希望能对同学们的学习有所帮助。

题目一：将下列数分解成质因数的乘积。

1. 12 =2. 16 =3. 28 =4. 36 =5. 48 =题目二：找出下列数的所有质因数。

1. 302. 423. 644. 755. 90题目三：将下列数分解成质因数的乘积。

1. 56 =2. 72 =3. 88 =4. 100 =5. 120 =题目四：请找出下列数的所有质因数。

1. 802. 983. 1084. 1265. 144题目五：将下列数分解成质因数的乘积。

1. 63 =2. 84 =3. 96 =4. 110 =5. 135 =解析：题目一：1. 12 = 2 × 2 × 3，所以分解质因数为 2 × 2 × 3。

2. 16 = 2 × 2 × 2 × 2，所以分解质因数为 2 × 2 × 2 × 2。

3. 28 = 2 × 2 × 7，所以分解质因数为 2 × 2 × 7。

4. 36 = 2 × 2 × 3 × 3，所以分解质因数为 2 × 2 × 3 × 3。

5. 48 = 2 × 2 × 2 × 2 × 3，所以分解质因数为 2 × 2 × 2 × 2 × 3。

题目二：1. 30 的质因数为 2、3、5。

2. 42 的质因数为 2、3、7。

3. 64 的质因数为 2。

4. 75 的质因数为 3、5。

5. 90 的质因数为 2、3、5。

分解质因数练习题
一：1：下面哪些数是合数，哪些是质数？是合数的分解质因数。

1，13，24，29，41，57，63，79，87
合数有：
质数有：
2：写出两个都是质数的连续自然数
3：写出两个既是奇数，又是合数的数
二：判断
1：任何一个自然数不是质数就是合数（）
2：偶数都是合数，奇数都是质数（）
3：7的倍数都是合数（）
4：20以内最大的质数乘以10以内最大的奇数，积是171
5：两个质数的积一定是质数（）
6:把28分解质因数的式子是28=1×2×2×7
7：45=5×3×3所以3，3，5分别是45的质因数（）
三：用短除法把下面各数分解质因数
65 56 94 78 122 189 77
四：在括号里填上合适的质数
15=（）×（）22=（）×（）
55=（）×（）91=（）×（）
39=（）×（）18=（）＋（）
24=（）＋（）28=（）＋（）
五：解决问题：
一个两位质数，交换十位与各位上的数，所得的两位数仍是质数，这个数是多少？
六：拓展：
边长为自然数，面积为105的形状不同的长方形共有多少种？。

五年级数学思维《分解质因数》专题训练
一、填空题（每小题6分，共60分）
1 有两个两位数的乘积是3927，这两个两位数的和是．
２ 151200有不少约数是两位数，这些两位约数中最大的是．
3 有五个连续奇数，它们的积是328185，则最大的一个奇数是．
4 一个质数的3倍与另一个质数的2倍之和为100，这两个质数的乘积是．
5 甲、乙、丙三人打靶，每人打了三枪，三个人各自中靶的环数之积
都是60，按个人中靶的总环数由高到低排列，依次为甲、乙、丙，则靶上4环的那一枪是打的．（环数是不超过10的正整数）
6 126共有个约数．
7 要使四个数的乘积135×1925×486×( )结果的最后五位数字
都是零，括号中的数最小应填．
8 三个年龄不到10岁的儿童在一起玩耍，已知她们的年龄之积为
90，那么她们的年龄之和为．
9 把5、6、7、14、15这五个数分成两组，使每组数的乘积相等，
这两组数分别为和．
10 200至220之间有唯一的质数，它是．
二、解答题（每小题20分，共60分）
11 将质数373拆开（不改变各数字间的顺序），所有可能只有3、
7、37、73这四种悄况，它们均是质数，请找出所有具有这样性
质的两位和两位以上的质数．
12 有三个自然数，最大的比最小的大6，另一个是它们的平均数，
且三数的乘积是42560，求这三个自然数．
13 有分别写有数字1、2、3、4、5、6、7、8、9的这9张纸牌中，
甲、乙、丙三人各拿3张．
甲说：“我的3张牌上数字的积是48.”
乙说：“我的3张牌上数字的和是15.”
丙说：“我的3张牌上数字的积是63.”
间：他们各拿了哪3张牌？。

第9讲分解质因数第一关【例1】把60分解质因数是60=1×2×2×3×5．（判断对错）×【答案】×【例2】把60分解质因数。

【答案】2×2×3×5【例3】请把下面的数分解质因数：（1）160；（2）598；（3）211【答案】（1）160=2×2×2×2×2×5；（2）598=2×13×23；（3）211=1×211【例4】把1112111这个对称的数分解质因数。

【答案】7×11×11×13×101【例5】像2，3，5，7 这样的只能被1和自身整除的大于1的自然数叫做质数或者素数．每一个自然数都能写成若干个质数（可以相同）的乘积，比如，4=2×2，6=2×3，8=2×2×2，9=3×3，10=2×5等，那么2×3×5×7-1写成这种形式为________________。

【答案】11×19【例6】像2，3，5，7这样只能被1和自身整除的大于1的自然数叫做质数或素数．每一个自然数都能写成若干个（可以相同）质数的乘积，比如，4=2×2，6=2×3，8=2×2×2，9=3×3，10=2×5等，那么，2×2×2×2×3×3-1写成这种形式为________________。

【答案】11×13【例7】像2，3，5，7这样只能被1和自身整除的大于1的自然数叫做质数或素数．每一个自然数都能写成若干个（可以相同）质数的乘积，比如，4=2×2，6=2×3，8=2×2×2，9=3×3，10=2×5等，那么，1938写成这种形式为________________。

五年级分解质因数练习题姓名班级1、找出下列数中的合数，再将合数分解质因数。

17 23 59 72 89 91 972、将下列各数分解质因数。

30 105 3603、三个连续的自然数的乘积是210，求这三个自然数。

4、有4个学生，他们的年龄恰好是一个比一个大1岁，而他们年龄的乘积是5040。

问他们年龄各是多少？5、求出60和360各数各有多少个因数？6、48与72的因数各有多少个？7、要使975×935×972×（）的乘积的最后四位数字为0，在括号里最小可以填数字是多少？8、要使135×115×35×（）的乘积的最后三位数字为0，在括号里最小可以填数字是多少？9、一个整数a与1080的乘积是一个完全平方数，求出a的最小值是？与这个平方数。

10、一个长方形的面积是51平方厘米，长和宽都是大于1的自然数，这个长方形的周长是多少？11、一次数学考试后，小明问老师自己得了多少分，老师说：“你的年龄与名次，得分乘积是1940，那么小明的年龄，名次，得分分别是多少？12、有两个数，已知其中一个数是另一个数的五倍，这两个数的积是3920，那么这两个数分别是？13、两个质数的和是39，求这两个质数的积是多少？14、王老师带领一班同学去植树，学生恰好分成4组，如果王老师和同学每人植树一样多，那么他们一共植树539棵。

这个班有多少学生？每人植树多少棵？15、如果两位数乘以两位数的积是2009，那么这两位数的和是（）16、求1650的因数个数？17、要使46×455×275×（）的乘积的最后四位数字为0，在括号里最小可以填数字是多少？18、一个整数甲与318的积正好是一个完全平方数乙，求甲最小是几？乙是几？参考答案1、72=2×2×2×3×3 91=7×132、30=2×3×5 105=3×5×7 360=2×2×2×3×3×53、210=2×3×5×74、 7、8、9、105、60=2×2×3×5 3×2×2=12个360=2×2×2×3×3×5 4×3×2=24个6、48=2×2×2×2×3 5×2=1072=2×2×2×3×3 4×3=127、208、2415=3×5×7×239、1080=2×2×2×3×3×3×5 2×3×5=302×2×3×3×5=18010、51=3×17 （3+17）×2=4011、1940=2×2×5×97 10岁第2名97分12、3920÷5=784 784=28×28 28×5=14013、2＋37=39 2×37=7414、539=7×7×11 学生48人，每人植树11棵15、2009=41×49 41+49=9016、1650=2×3×5×5×11 2×2×2×3=24（个）17、4018、318=2×3×53 318 318×318=101124。

五年级分解质因数练习题1.找出下列数中的合数，再将合数分解质因数：72（2^3× 3^2）、91（7 × 13）2.将下列各数分解质因数：30（2 × 3 × 5）、105（3 × 5 ×7）、360（2^3 × 3^2 × 5）3.三个连续的自然数的乘积是210，求这三个自然数：4、5、64.有4个学生，他们的年龄恰好是一个比一个大1岁，而他们年龄的乘积是5040.问他们年龄各是多少：5、6、7、85.求出60和360各数各有多少个因数：60（12个因数）、360（24个因数）6.48与72的因数各有多少个：48（10个因数）、72（12个因数）7.要使975×935×972×（）的乘积的最后四位数字为，在括号里最小可以填数字是多少：48.要使135×115×35×（）的乘积的最后三位数字为，在括号里最小可以填数字是多少：29.一个整数a与1080的乘积是一个完全平方数，求出a的最小值是与这个平方数：1510.一个长方形的面积是51平方厘米，长和宽都是大于1的自然数，这个长方形的周长是多少：20厘米11.一次数学考试后，XXX问老师自己得了多少分，老师说：“你的年龄与名次，得分乘积是1940，那么XXX的年龄，名次，得分分别是多少：10岁、17名、114分12.有两个数，已知其中一个数是另一个数的五倍，这两个数的积是3920，那么这两个数分别是：28和14013.两个质数的和是39，求这两个质数的积是多少：19014.XXX带领一班同学去植树，学生恰好分成4组，如果XXX和同学每人植树一样多，那么他们一共植树539棵。

这个班有多少学生每人植树多少棵：13个学生，每人植41棵树15.如果两位数乘以两位数的积是2009，那么这两位数的和是：6316.求1650的因数个数：24个因数17.要使46×455×275×（）的乘积的最后四位数字为，在括号里最小可以填数字是多少：2。

小学分解质因数练习题一、填空1、在自然数中，既不是质数也不是合数，在偶数中，是质数．2、在自然数中，既是奇数又是质数的最小的数是，既是一位数奇数又是合数，既是偶数又是质数，既不是质数又不是合数．一个合数至少有个约数．3、用三个一位质数组成能同时被3和5整除的三位数，其中最大的是，最小的数是．、10～20之间的质数有，其中个位上的数字与十位上的数字交换位置后，仍是一个质数．、在1、2、4、10、11这几个数中，是整数，是奇数，是偶数，是质数，是合数．6、20以内差为4的两个质数是和，和，和．7、用最小的质数，最小的奇数，最小的合数和0组成一个四位数，其中能够被2和5同时整除的最大四位数是，只能被2整除的最小四位数是．8、28的约数有，这些数中，质数有，合数有，奇数有，偶数有．9、把下面各数分别填在指定的圈里．9、23、31、39、41、51、69、79、81、89、91、97二、判断1、能被2整除的数都不是质数．、在自然中，除2以外，所有的偶数都是合数．、边长是质数的正方形，它的周长一定是合数．4、只有两个约数的自然数一定是质数．5、自然数中只有质数和合数．、自然数中除了质数、合数，还有1．7.所有的质数都是奇数．8、有三个或三个以上约数的数一定是合数．9、合数有约数，质数没有约数． 10、两个质数的乘积一定是合数． 11.所有合数都是偶数． 12、除了2和5这两个数以外，个位上是0、2、4、6、8、5的数都是合数．三、按要求写数．1、一个四位数，个位上的数既不是质数也不是合数，十位上的数既是质数又是偶数，百位上的数是最小的合数，千位上的数既是奇数又是合数，这个四位数是、能同时被3、5整除的最小的三位数是3、两个质数和为18，积是65，这两个质数是和．4.用10以内的质数组成一个三位数，使它能同时被3、5整除，这个数最小是，最大是。

5.在括号里填上适当的质数①8=＋②12=＋＋③15=＋④18=＋＋⑤24=＋=＋=＋6.两个质数的和是18，积是65，这两个质数分别是多少？7.当a分别是1、2、3、4、5时，6a＋1是质数，还是合数?8.分解质因数。

学前数学简单质因数分解练习题质因数分解是数学中的一项基本技巧，能够帮助我们将一个数分解成几个较小的质数的乘积。

在学前阶段，我们可以通过一些简单的练习题来帮助孩子们理解和掌握这一概念。

下面是一些适合学前儿童的简单质因数分解练习题。

1. 将数字10进行质因数分解。

解答：10可以分解为2乘以5。

2. 将数字24进行质因数分解。

解答：24可以分解为2乘以2乘以2乘以3。

3. 将数字35进行质因数分解。

解答：35可以分解为5乘以7。

4. 将数字48进行质因数分解。

解答：48可以分解为2乘以2乘以2乘以2乘以3。

通过这些简单的练习题，孩子们可以逐渐理解质因数分解的概念，并掌握如何将一个数进行分解。

希望以上练习题对学前儿童的数学学习有所帮助。

通过这些简单的质因数分解练习，他们可以逐步提高数学思维能力，并为以后更复杂的数学题目打下基础。

数学是一门需要反复练习和探索的学科，只有通过不断的实践和思考，孩子们才能真正理解和运用数学知识。

在教学过程中，教师可以采用互动的方式，鼓励孩子们参与其中。

例如，可以用彩色的图形或图片来表示质因数分解的过程，让孩子们通过观察和讨论，逐渐形成对质因数分解的理解。

同时，可以设计一些趣味性的小游戏或活动，让孩子们在玩耍中掌握质因数分解的方法。

除了以上的练习题，还可以自行扩展其他数字的质因数分解练习题，根据孩子们的年龄和数学水平来选择适当的题目。

逐步增加难度，帮助他们不断提高数学思维和解题能力。

总结起来，学前数学的简单质因数分解练习题对于培养孩子们的数学思维和解题能力非常重要。

通过实践和讨论，让孩子们逐步理解质因数分解的概念，并能够灵活运用于解决简单的数学问题。

希望通过这些练习题的学习，能够为孩子们今后的数学学习打下坚实的基础。

分解质因数运用10例(详解)例1、已知360×A=B×B，其中A、B均为自然数，求A的最小值是几？B的值又为几？分析与解答：因为360×A=B2，即为360×A也是一个完全平方数。

而360=5×3×3×2×2×2=（5×3×2）×（3×2×2），因此可得要使360×A是一个完全平方数，A的值只能为：5×2=10。

所以可得，A 的值最小为10。

这时B的值为60。

例2、A、B、C均为自然数，已知A×B=132，B×C=156，C×A=143。

求A×B×C的值是几？分析与解答：因为132=11×12，所以A×B =11×12。

156=12×13，所以B×C =12×13。

143=11×13，所以C×A =11×13。

比较以上各式可知，A=11；B=12；C=13。

所以A×B×C=11×12×13=1716。

例3、把棱长1厘米的小正方体2100个，堆在一个实心的大长方体，这个长方体的高为10厘米，并且长、宽均大于高，求这个长方体的表面积。

分析与解答：根据题中的条件可知，这个长方体的体积为2100立方厘米，因为长方体的高为10厘米，所以长方体的底面积为：2100÷10=210（平方厘米）。

又因为长方体的长、宽均大于10。

而210=2×5×3×7=（3×5）×（2×7）=15×14。

因此可得，这长方体的长为15厘米，宽为14厘米，高为10厘米。

它的表面积为：（15×14+15×10+14×10）×2=1000（平方厘米）。