数值传热学1

1. 质量守恒方程：单位时间内微元体中流体质量的增加=同一时间间隔内流入该微元体的净质量2. 动量守恒方程：微元体中流体动量的增加率=作用在微元体上各种力之和3. 能量守恒方程：微元体内热力学能的增加率=进入微元体的净热量+体积力与表面力对微元体做的功4. 控制方程的通用形式：展开形式：5. 控制方程的守恒与非守恒形式对比：1.从微元体的角度，控制方程的守恒形式与非守恒形式是等价的，都是物理的守恒定律的数学表示。

2.从数值计算的观点，守恒型的方程有两个优点。

A 守恒型的控制方程可以使激波的计算结果光滑而且稳定，而应用非守恒型方程时激波的计算结果会在激波前及后引起解的振荡，并导致错误的激波位置。

B 只有守恒型的控制方程才可以保证对有限大小的控制容积内所研究的物理量的守恒定律仍然得到满足。

6. 初始条件是所研究现象在过程开始时刻的各个求解变量的空间分布，必须予以给定。

对于稳态问题不需要初始条件。

边界条件是在求解区域的边界上所求解的变量或其一阶导数随地点及时间的变化规律。

7. 二维稳态层流控制方程：质量守恒方程：0=∂∂+∂∂yv x u动量守恒方程：)(1)()(2222yu xu xpy vu x uu ∂∂+∂∂+∂∂-=∂∂+∂∂νρ)(1)()(2222yv xv ypyvv x uv ∂∂+∂∂+∂∂-=∂∂+∂∂νρ能量守恒方程：)()()(2222yT xT a yvT xuT ∂∂+∂∂=∂∂+∂∂8. 偏微分方程的三种类型：双曲型b2-4ac>0，过该点有两条实的特征线；抛物型b2-4ac=0过该点有一条实的特征线；椭圆型b2-4ac<0过该点没有实的特征线。

9. 椭圆型方程：描写物理学中一类稳态问题，这种物理问题的变量与时间无关而需要在空间的一个闭区域内来求解。

这类问题又称边值问题。

稳态导热过程，有回流的流动与对流换热都属于椭圆型问题，其控制方程都是椭圆型的。

抛物型方程描写物理学中一类步进问题，这类问题中因变量与时间有关，或问题中有类似于时间的变量。

数值传热学 -回复
数值传热学（Numerical Heat Transfer）是一门研究热传递现象的学科，通过数值模拟和计算方法来分析热传导、对流和辐射等传热过程。

本文将介绍数值传热学的基本原理、方法和应用。

1. 基本原理
数值传热学基于传热学原理和计算数学方法，将传热过程建模为数学方程，并通过数
值方法求解这些方程，从而得到热传递的数值解。

主要的传热模型包括热传导、对流和辐
射传热。

2. 数值方法
数值传热学常用的方法包括有限差分法、有限元法和边界元法等。

有限差分法是最常
用的方法之一，将传热区域离散化为网格，通过差分近似计算网格点上的温度或热流量。

有限元法则是另一种常用的方法，将传热区域划分为元素，通过建立元素之间的关系来计
算温度场或热流场。

边界元法则是将问题转化为边界上的积分方程，通过求解积分方程得
到温度场或热流场。

3. 应用领域
数值传热学在各个领域都有广泛的应用。

在工程领域，数值传热学用于优化热交换器
的设计、预测电子器件温度分布、模拟流体在管道内的传热过程等。

在材料科学领域，数
值传热学用于研究材料的导热性能、相变过程以及焊接和烧结等工艺。

在能源领域，数值
传热学用于分析太阳能热收集器的性能、燃烧过程中的传热机制等。

通过数值传热学的研究，我们可以更加深入地了解热传递过程，并可以通过数值模拟
方法来预测和优化热传递的效果。

数值传热学也为各个领域的工程和科学研究提供了重要
的工具和方法。

通过不断的发展和创新，数值传热学将进一步推动热传递理论和应用的发展。

数值传热学是热力学的重要分支之一，研究物质中热量的传递和分布规律。

与传统的实验方法相比，数值传热学采用计算机模拟技术，通过数学模型和计算实验方法，能够更加深入、系统地研究热传递现象的规律和特性，为工程设计和实际生产提供重要的技术支持。

数值传热学的本质是热传递方程的数值求解。

热传递方程是描述物质中热量传递和分布的方程，它包含了热传导、热对流和热辐射三种传热方式。

热传导是指热量沿着物质内部的温度梯度传递，主要发生在固体和液体中；热对流是指热量随物质的流动而传递，主要发生在液体和气体中；热辐射是指热量通过辐射传递，主要发生在光学和辐射热转换材料中。

通过数值方法求解热传递方程，可以得到物体的温度分布、热传递速率和热流密度等参数，为材料和工程设计提供准确的数据支持。

数值传热学的核心是数值方法，主要包括有限差分、有限元和边界元等方法。

有限差分法是一种利用离散化方法求解微分方程的数值方法，它将微分方程中的连续变量离散化，将求解微分方程转化为求解线性方程组。

有限元法是一种利用有限元逼近方法解决偏微分方程的数值方法，采用对物体进行简单的几何划分，将问题离散化，通过数学建模来表示物体的温度分布和热流密度分布。

边界元法是一种较新的有限元法补充，它能够快速解决边界值问题，并且可以减少问题的维数。

数值传热学的应用范围广泛，包括热工和物理问题的研究、能源系统分析和设计、建筑工程中的热传递和能源效率研究等。

例如，在太阳能发电系统设计中，数值传热学可以帮助设计人员确定集热器表面温度和吸收率等参数，提高太阳能效率并减少系统成本。

在建筑工程中，数值传热学可以帮助设计师分析建筑物的保温性能，合理评估保温材料的性能和使用效果，确保建筑节能和环保。

在机械加工领域中，数值传热学可以帮助工程师分析材料切削过程中的热量和温度分布，挑选适合材料和刀具的加工工艺，提高机械切削效率。

数值传热学是现代科学技术的重要分支之一，是研究物质中热传递和分布规律的重要工具。

热流问题的数值计算Numerical Simulations of Thermal & Fluid Problems第一章 绪论主讲 陶文铨西安交通大学能源与动力工程学院 热流中心 CFD-NHT-EHT CENTER 2007年10月16日, 西安1/88物理问题数值解的基本思想 把原来在空间与时间坐标中连续的物理量的场 (如速度场,温度场,浓度场等),用一系列有限 个离散点(称为节点,node)上的值的集合来代替; 通过一定的原则建立起这些离散点上变量值之间关 系的代数方程 (称为离散方程,discretizationequation);求解所建立起来的代数方程以获得所求解变量的近似解.2/88大规模科学计算的重要性 传热与流动问题数值计算是应用计算机求解热量传 递过程中的速度场,温度场等的分支学科,是大规模 科学计算的重要组成部分,其重要性不言而喻. 2005年美国总统顾问委员会向美国总统提出要大 力发展计算科学以确保美国在世界上的竞争能力. 波音公司实现了对航空发动机的网格数达10亿量 级的直接数值模拟,以研究所设计发动机的性能.3/88现代科学研究的三大基本方法及其关系理论分析Analytical实验研究Experimental数值模拟Numerical4/88课程简介1. 学时- 30学时理论教学;6学时计算机作业 2. 考核- 平时作业/计算机大作业/考试: 20/30/50 3. 方法- 理解,参与,应用 努力将与数学处理相对应的物理背景联系起来理解. 4. 助手- 于乐 5. 参考教材-《计算流体力学与传热学》,中国建筑 工业出版社,19915/88学习方法建议1. 善于从物理过程基本特性来掌握理解数值方法; 2. 对数值方法-明其全而析其微:明其全-了解基本原理;析其微-掌握实施细节;3. 努力上机实践; 4. 学会分析计算结果: 合理性,规律性; 5. 应用商业软件与自编程序相结合.6/88《热流问题的数值计算》 主要教学内容第一章 绪论(物理与数学基础) 第二章 一维导热问题的数值解 第三章 多维导热问题的数值解 第四章 势流及管道内充分发展流动与换热的数值解 第五章 有回流的动与换热问题的数值解 第六章 二维涡量-流函数法通用程序介绍 第七章 原始变量法与湍流数值模拟简介7/88绪论1.1 流动与传热问题控制方程的基本类型 1.2 流动与传热问题数值计算的基本步骤 1.3 建立离散方程的方法 1.4 离散方程数学与物理特性分析简介8/881.1 流动与传热问题控制方程的基本类型1.1.1 流动与传热问题完整的数学描写 1.1.2 控制方程 1. 质量守恒方程 3. 能量守恒方程 1.1.3 单值性条件 1.1.4 建立数学描写举例 1.1.5 控制方程式的分类9/882. 动量守恒方程1.1 流动与传热问题控制方程的基本类型1.1.1 流动与传热问题完整的数学描写 1. 有关的守恒定律的偏微分方程(控制方程)一切宏观的流动与传热问题都由三个守恒定律所 支配:质量,动量与能量守恒(conservation law).2. 与表述守恒定律的偏微分方程相关的单值性条件.不同问题的区别主要在于单值性条件 (conditions for unique solution) 的不同:初始条件以,边界条件 以及物性数据.10/881.1.2 控制方程(Governing equations) Mass conservation1. 质量守恒方程r ( r u ) ( r v) ( r w) + + + =0 t x y z单位时间 内质量的 增加 单位时间内流 进微元体的净 质量物理意义:单位时间内空 间某一微元容积质量的增 加等于流入该微元容积的 净质量.11/88对不可压缩流体: r = const 对二维不可压缩流体:u v + =0 x yu v w + + =0 x y z对二维问题,速度矢量:ur u v 数学上称: + = div(U ) x yur r ur U =ui+v j为速度矢量的散度,因此对二维不可压流体有:ur div(U ) = 0下面只讨论不可压缩流体(incompressible flow).12/882. 动量守恒方程(Momentum conservation)对上图所示的微元体分别在三个坐标方向上应用 Newton第2定律(F=ma)在流体中的表现形式: [微元体内动量的增加率]=[作用在微元体上各种力之和] 可得出三个坐标方向的动量方程:u uu uv uw 1 p 2u 2u 2u + + + =+ n ( 2 + 2 + 2 ) + Fx t x y z r x x y z 1 p v vu vv vw 2v 2v 2v + + + =+ n ( 2 + 2 + 2 ) + Fy t x y z r y x y z 1 p w wu wv ww 2 w 2 w 2 w + + + =+ n ( 2 + 2 + 2 ) + Fz t x y z r z x y z微元体内动 量的增加率压力粘性力体积力13/883. 能量守恒方程(Energy conservation)[微元体内热力学能的增加率]=[通过流动与导热进入 微元体内的净热流量]+[体积力与表面力对微元体所做 的功率] 引入导热Fourier定律,假定热物性为常数,可得T (uT ) (vT ) ( wT ) 2T 2T 2T rcp[ + + + ] = l( 2 + 2 + 2 ) + S t x y z x y z微元体 内能增 加率 由于流动被带出 微元体的净功率 由于导热而进入 源项 微元体的净功率 生成 热14/88l =a rcp流体的热扩散率(thermal diffusivity)4. 对于二维稳态对流换热问题控制方程汇总u v + =0 x yuu uv 2u 2u 1 p + =+ n ( 2 + 2 ) + Fx y z r x x yvu vv 2v 2v 1 p + =+ n ( 2 + 2 ) + Fy y z r y x y(uT ) (vT ) 2T 2T + = a( 2 + 2 ) + ST x y x y对流项扩散项源项数值计算中常用的术语.15/88不同的二维,稳态求解问题之间的区别在于: (1)边界条件不同; (2)源项与扩散系数不同.5. 二点说明1. 所导出的三维非稳态Navier-Stokes方程,无论对 层流或是湍流都是适用的. 2. 辐射换热需要用积分方程来描述,课程中将不涉及 这类问题.16/881.1.3 单值性条件 1. 初始条件 2. 边界条件 (1) 第一类 (Dirichlet):t = 0, T = f ( x, y, z )TB = Tgiven(2) 第二类 (Neumann): qB = -l (T ) B = qgiven n(3) 第三类 (Rubin):规定了边界上被求函数的一阶导数与函数之间的关系: -l ( T ) B = h(TB - T f )n数值计算中计算区域的出口边界条件常常最难 确定,要做近似处理.17/881.1.4 建立数学描写举例 1. 问题与假设条件突扩区域中的对流传热:二维,稳态,不可压缩, 常物性,不计重力与黏性耗散.18/882. 控制方程u v + =0 x y1 p u u u u u +v =+n ( 2 + 2 ) r x x y x y 2 2 v v 1 p v v u +v =+n ( 2 + 2 ) x y r y x y2 2T T T T u +v = a( 2 + 2 ) x y x y2 219/883. 边界条件 (1)进口边界条件:给定u,v,T随y 的分布; (3)中心线: u = T = 0; v = 0 y y(4)出口边y x界:数学上要 求给定u,v,T 或其导数随y 的分布;实际 上做不到;数 值上近似处理20/88(2)固体边界条件:速度无滑移,温度无跳跃1.1.5 传热与流动问题的数学描写的分类 1. 从数学角度分类-椭圆型与抛物型椭圆型 (Elliptic)椭圆型方程数学上的特点是:所求解的因变量对每个 空间自变量均存在二阶导数项: 导热方程-所求解的因变量为温度T ,空间自变量x,y; 动量方程-所求解的因变量为速度u ,空间自变量x,y.21/88抛物型(Parabolic)抛物型方程数学上的特点是:所求解的因变量对某个 个自变量只存在一阶导数项: 非稳态导热方程-因变量T 对时间t仅有一阶导数; 边界层动量方程-u对空间自变量x仅有一阶导数. 仅存在一阶导数的自变量在物理过程上的重要特 点:过程只能沿该坐标的单个方向进行而不能逆向进 行.22/88抛物型与椭圆型流动的例子椭圆型方程的求解必须全场联立进行,而抛物性 方程的求解可以沿坐标正向逐步推进, 大大节省时间.23/88(1)椭圆型问题: 流动有回流,必须 全场同时求解; (2)抛物型问题:流动无回流,可以沿主流方向步 步逼进,不必全场同时求解,大大节省时间.Marching method24/882. 从物理角度分类-守恒型与非守恒型守恒型( Conservative)-对任意大小容积守恒特性 都能得到满足的方程; 凡对流项表示成散度形式的方程具有守恒性 . 非守恒型方程+u v v u u v u ++ u = 0= 0 u ( + ) = 0 x x y y x y (uu ) (uv) 1 p 2u 2 v =+n ( 2 + 2 ) + r x x x y x守恒型方程凡是从守恒型控制方程推导得到的用于数值求解 的代数方程也具有守恒特性.25/881.2 流动与传热问题数值求解的基本步骤1.2.1 流动与传热问题数值求解步骤 1. 建立数理模型 3. 方程的离散化 5.代数方程求解 1.2.2 区域离散化方法 2.区域的离散化 4. 边界条件离散 6. 求解结果分析1.区域离散化的任务 2. 区域离散方法1.2.3 网格系统标记方法26/881) 外节点法2. 内节点法1.2.1 流动与传热问题数值求解步骤把原来在空间与时间坐标中连续的物理量的场 (如速度场,温度场,浓度场等),用一系列有限个 离散点(称为节点,node)上的值的集合来代替;通过 一定的原则建立起这些离散点上变量值之间关系的代 数方程(称为离散方程,discretization equation);求 解所建立起来的代数方程以获得所求解变量的近似解.27/88(1) 区域离散 (2) (3) (4) (5) 代数求解 (6)28/88方程离散结果分析1.2.2 区域离散化1.区域离散化的任务将所计算的区域分割成许多不重叠的子区域,确 定每个子区域中节点的位置以及所代表的控制容积. 离散结果得出四种几何要素: (1) 节点(node):所求解未知量的位置; (2) 控制容积(control volume):实施守恒定律的最 小几何单位; (3) 界面(interface):控制容积的分界位置; (4) 网格线(grid lines):沿坐标方向相邻节点连接 成的曲线簇.29/882. 区域离散方法 (a) 外节点法:节点位于子区域的角顶;控制容积界 面位于两节点之间;生成过程:先节点后界面;又 称 Practice A.子区域控制容积30/88YPractice A-外节点法 x31/88(b) 内节点法:节点位于子区域的中心;子区域即为 控制容积;生成过程:先界面,后节点,又称 Practice B.子区域即为控制容积32/88YPractice B-内节点法 x33/88 1.2.3 内接点与外节点法的比较 (a)边界节点所代表的控制容积不同 方法A 边界节点代表半个CV方法B 边界节点代表零个CV(b)网格非均分时,节点作为控制容积的代表方法B 更合理 方法A 方法B34/881.2.3 网格系统表示方法 网格线-节点间连线,用实线表示;界面为虚线; 节点间距离-dx;界面间距离-Dx .35/881.2.4 网格独立解 当网格足够细密以至于再进一步加密网格已对 数值计算结果基本上没有影响时所得到的数值解称 为网格独立解(grid-independent solution).Int. Journal Numerical Methods in Fluids, 1998, 28: 1371-1387.36/881.3 建立离散方程的方法 1.3.1 一维模型方程( 1-D model equation ) 1.3.2 由Taylor 展开法导出导数的差分表示式 1.3.3 控制容积积分法导出导数的差分表示式 1.3.4 讨论37/881.3 建立离散方程的方法 1.3.1 一维模型方程( 1-D model equation ) 一维模型方程是一维非稳态有源项的对流-扩 散方程,具有四个特征项,便于离散方法的研讨. 非守恒型 守恒型 ( rf ) f f + ru = (G ) + Sf t t x xFDM采用 ( rf ) ( r uf ) f + = (G ) + Sf FVM采用 t t x x 瞬态 对流 扩散 源项38/88"麻雀虽小,五脏俱全!"1.3.2 由Taylor 展开法导出导数的差分表示式 1. 一阶导数的差分表达式的导出 将函数f ( x, t ) 在(i+1,n)的值对(i,n)点做Taylor展开:f 2f Dx 2 2 f (i + 1, n) = f (i, n) + )i ,n Dx + 2 )i ,n Dx + ..... x x 2!f f (i + 1, n) - f (i, n) Dx 2f ) i ,n = - ( 2 )i ,n + ... x Dx 2 x39/88O ( Dx ) 称为截断误差, truncation error,表示:随 Dx 的趋于零,用 f (i + 1, n) - f (i, n) 代替 f )i ,n 的误差 x Dxf f (i + 1, n) - f (i, n) )i ,n = + O(Dx) x Dx KD x, K 与 Dx 无关.D x 的方次称为截差的阶数(order of TE).用数值计算的近似解 fin 代替精确解 f (i, n)fin 1 - fin f )i ,n @ + , O(Dx) 得向前差分: x Dx40/88f -f f )i ,n @ 向后差分: x Dxn in i -1, O (Dx )fin 1 - fin 1 f )i , n @ + , O(Dx 2 ) 中心差分: x 2Dx2. 一,二阶导数的各种差分表达式. 表达差分结构的格式图案o构筑差分表达式的位置; 构筑差分表达式所用到的节点.41/88一阶导数的 常用差分表达式42/88二阶导数的常用差分表达式定性判别导数的差分表达式正确与否的方法: (1)量纲是否正确-与导数本身一致; (2)均匀场的各阶导数应为零.43/883. 一维模型方程的有限差分显式离散表示式 微分方程形式: 假设 ( rf ) f f + ru = (G ) t t x xr , u, G均为常数,显式差分表达式:fin +1 - fin fin 1 - fin 1 r + ru + = Dt 2Dx fin 1 - 2fin + fin 1 G + , O (Dt , Dx 2 ) Dx 2差分方程 截断误差44/88显式(Explicit)-空间导数均以初 始时刻之值计算.1.3.3 控制容积积分法导出导数的差分表示式 1. 控制容积积分法实施步骤 1. 将守恒型的方程对控制容积做积分; 2. 选定被求函数及其一阶导数对时间,空间的变化 曲线-型线; 3. 完成积分,整理成相邻节点间未知量的代数方程. 2. 两种常用型线 型线-被求函数随自变量的局部变化方式,本是 所求内容,近似求解需先假定.45/88随空间自变量的变化型线 型线 型线分段线性阶梯逼近46/88piece-wise linear step-wise approximation随时间自变量的变化型线分段线性 piece-wise linear阶梯逼近 step-wise approximation47/883. 一维模型方程的控制容积积分法离散 将守恒型控制方程对控制容积P 在[t, t+ Dt ]内 做积分, ( rf ) ( r uf ) ft立即可得e+xt +Dt t=xe(Gx)r ò (ft +Dt -ft )dx +rwò [(uf)òt- (uf)w ]dt =t +Dt=Gf f [( )e - ( ) w ]dt x xf 以及 x48/88继续积分,需要知道:f对空间与时间的变化型线.1. 非稳态项假设 f 对空间呈阶梯型变化:t t r ò (f t +Dt - f t )dx = r (f P+Dt - f P )Dx w e2. 对流项假设 f 对时间呈显示阶梯型变化:rt +Dtòt[(uf )e - (uf ) w ]dt = r[(uf )te - (uf )tw ]Dt49/88假设 f 对空间呈分段线性变化:fE + fP fP + fW fE - fW r[(uf ) - (uf ) ]Dt = r uDt ( ) = r uDt 2 2 2t e t w均分网格3. 扩散项f 假设 对时间呈显式阶梯型变化: xt +DtGòtf f f t f t [( )e - ( ) w ]dt = G[( )e - ( ) w ]Dt x x x x50/88假设 f 对空间呈分段线性变化:。

数值传热学习题答案数值传热学习题答案数值传热学是热力学的一个重要分支，主要研究热量在物质中传递的机理和规律。

在实际工程中，我们经常会遇到各种与传热有关的问题，通过数值计算可以得到准确的答案。

下面我将为大家提供一些数值传热学习题的答案，希望能够帮助大家更好地理解和应用这门学科。

1. 一个铝制热交换器的表面积为10平方米，其表面温度为100摄氏度，环境温度为20摄氏度。

已知铝的导热系数为200 W/(m·K)，求热交换器的传热速率。

答：根据传热定律，传热速率与传热面积、传热系数和温度差之间成正比。

传热速率 = 传热系数× 传热面积× 温度差。

将已知数据代入公式中，可得传热速率= 200 × 10 × (100 - 20) = 160,000 W。

2. 一个房间的尺寸为5米× 5米× 3米，墙壁和天花板的厚度为0.2米，墙壁和天花板的导热系数为0.5 W/(m·K)，室内温度为25摄氏度，室外温度为10摄氏度。

求房间的传热损失。

答：房间的传热损失可以通过计算墙壁和天花板的传热速率来得到。

墙壁和天花板的传热速率 = 传热系数× 传热面积× 温度差。

墙壁和天花板的传热面积 = 2 × (5 × 5) + 2 × (5 × 3) = 70平方米。

将已知数据代入公式中，可得墙壁和天花板的传热速率= 0.5 × 70 × (25 - 10) = 525 W。

因此，房间的传热损失为525瓦特。

3. 一个水箱的体积为1立方米，初始温度为20摄氏度，水的密度为1000千克/立方米，比热容为4186 J/(千克·摄氏度)，水箱的表面积为2平方米，表面温度为100摄氏度。

已知水的传热系数为0.6 W/(m^2·K)，求水箱内水的温度随时间的变化。

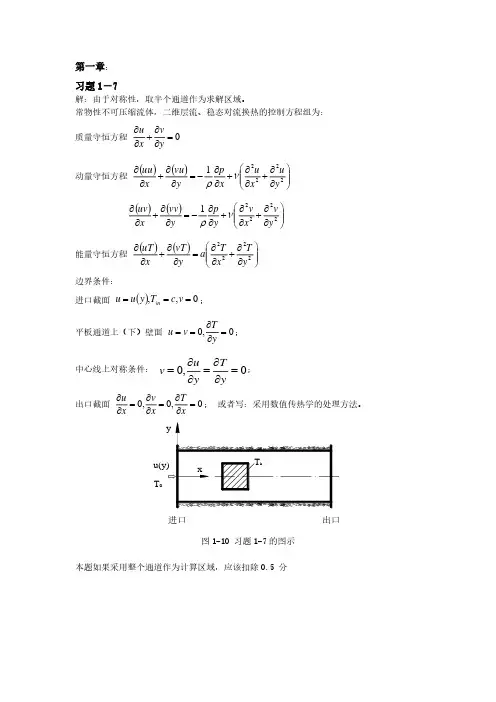
数值传热学的通用方程数值传热学的通用方程引言：传热学是研究热量在物体内传递的学科，它在实际生活中具有广泛的应用。

数值传热学是传热学的一个重要分支，借助数值计算方法和计算机模拟，能够更准确地预测和模拟热量的传递过程。

在数值传热学中，通用方程是一种重要的工具，它能够描述和计算物体内热量的传递方式。

本文将以数值传热学的通用方程为主题，通过分析其深度和广度，以全面评估和解释这一概念。

一、数值传热学的基础概念1.1 热量传递的三种方式热量传递有三种方式：传导、对流和辐射。

传导是指热量通过物质的直接接触和振动传递，对流是指热量通过流体的传输，辐射是指热量通过电磁波辐射传递。

这三种方式在不同的情况下起着不同的作用，同时它们也相互影响和耦合。

1.2 数值计算方法在传热学中的应用数值计算方法是数值传热学的核心工具，它可以通过数学模型和离散计算，模拟和预测物体内热量的传递过程。

常用的数值计算方法有有限元法、有限差分法和有限体积法等。

通过这些方法，我们可以更准确地计算和研究热量的传递规律。

二、数值传热学的通用方程2.1 传热方程的基本形式传热方程是描述热量传递过程的数学方程，它以物体内部的温度分布、热流和热导率等参数为基础，通过各种数学方法和推导，得到不同传热方式下的通用方程。

2.2 热传导方程热传导方程是描述热量通过传导方式传递的方程。

在传热过程中，热量会从高温处传向低温处，而传热率又与温度梯度和材料的热导率成正比。

热传导方程能够计算和描述热量在物体内部的传递过程，为热传导问题的分析和计算提供了基础。

2.3 流体传热方程流体传热方程是描述热量通过对流方式传递的方程。

流体传热过程中，流体的流动状态和温度梯度会影响热量的传递速率。

流体传热方程能够计算和描述流体内部的热量传递过程，对于流体传热问题的研究和分析具有重要意义。

2.4 辐射传热方程辐射传热方程是描述热量通过辐射方式传递的方程。

辐射传热过程中，热量通过电磁波的辐射传输，与物体的温度和辐射特性有关。

数值传热学一维非稳态导热
数值传热学一维非稳态导热是一个拟表达热量输运多方面考虑下的相关分析技术，例如光斑热传递，带有间断层热传导，恒定物质热传导等等。

本文将重点简要介绍一维非稳态导热模型中的理论方法，为解决该问题提供重要基础。

首先，我们讨论的一维非稳态导热模型是一维的，在这种模型中，温度的变化是由上下相邻的单元格热传导加权平均值决定的，从一个单元格到另一个单元格的变化必须满足偏微分方程的通用表达式。

其次，根据以上的假设，一维非稳态导热的数值解将以定义的步长迭代，用于求解温度在不同单元中的变化。

在数值模拟中，需要对边界条件、热导率和温度输入进行有效描述，以确定最终的解答模式。

同时，本次分析中，利用有限差分和蒙特卡罗方法来求解温度场。

这种有趣且可行的做法，不但实现了所需求解的模式，而且能够精确地给出结果。

此外，在电脑指令中，采取该方法对数值运算很有效，从而提高了计算机解的精度和实现的质量。

最后，一维非稳态导热模型是在一定物理场中进行计算的，通用性很强，其能够很好地模拟简单模型中物理场的变化。

因此，它经常被用于诸如热管道传热、滑动轴热传导、负载温度场仿真等多种领域的研究。

总而言之，一维非稳态导热的数值模拟具有良好的数学基础、使用简单的算法以及电脑指令，从而实现快速求解热传导问题的目的，是今后研究的重要课题。

数值传热学数值传热又称计算传热，是传热学与数值方法相结合的一门交叉学科，它采用数值方法描述流动和传热问题的控制方程，并用计算机求解。

数值换热，其基本思想是将原始坐标在空间和时间上连续的物理量场（如速度场、温度场和浓度场等），用一系列有限个离散点上的数值来代替，通过一定的原理建立离散点变量值之间的关系代数方程（称为离散方程）。

通过求解所建立的代数方程组，得到求解变量的近似值。

1简介数值传热学（numerical heat transfer）数值传热学，又称计算传热学，是指对描写流动与传热问题的控制方程采用数值方法，通过计算机求解的一门传热学与数值方法相结合的交叉学科。

数值传热学的基本思想是把原来在空间与时间坐标中连续的物理量的场（如速度场，温度场，浓度场等），用一系列有限个离散点上的值的集合来代替，通过一定的原则建立起这些离散点变量值之间关系的代数方程（称为离散方程）。

求解所建立起来的代数方程已获得求解变量的近似值。

2发展简史数值传热学，主要由20世纪中叶，S.V. Patankar和D.B.Spalding 等人在总结前人的研究基础上所提出。

E.M.Sparrow对数值传热学的发展也起到了一定的促进作用。

国内比较知名的学者是陶文铨教授。

陶文铨3研究方法数值传热学常用的数值方法1.有限差分法历史上最早采用的数值方法，对简单几何形状中的流动与换热问题最容易实施的数值方法。

其基本点是：将求解区域中用于坐标轴平行的一系列网格的交点所组成的点的集合来代替，在每个节点上，将控制方程中每一个导数用相应的差分表达式来代替，从而在每个节点上，形成一个代数方程，每个方程中包括了本节点及其附近一些节点上的未知值，求解这些代数方程就获得了所需的数值解。

2.有限容积法将所计算的区域划分成一系列控制容积划分为一系列控制容积，每个控制容积都有一个节点做代表。

通过将守恒型的控制方程对控制容积坐积分导出离散方程。

在导出过程中，需要对界面上的被求函数本身及其一阶导数的构成做出假定，是目前流动与换热问题的数值计算中应用最广的一种方法。

数值传热学数值传热学（numerical heat transfer）数值传热学，又称计算传热学，是指对描写流动与传热问题的控制方程采用数值方法，通过计算机求解的一门传热学与数值方法相结合的交叉学科。

数值传热学的基本思想是把原来在空间与时间坐标中连续的物理量的场（如速度场，温度场，浓度场等），用一系列有限个离散点上的值的集合来代替，通过一定的原则建立起这些离散点变量值之间关系的代数方程（称为离散方程）。

求解所建立起来的代数方程已获得求解变量的近似值。

数值传热学（numerical heat transfer）数值传热学，又称计算传热学，是指对描写流动与传热问题的控制方程采用数值方法，通过计算机求解的一门传热学与数值方法相结合的交叉学科。

数值传热学的基本思想是把原来在空间与时间坐标中连续的物理量的场（如速度场，温度场，浓度场等），用一系列有限个离散点上的值的集合来代替，通过一定的原则建立起这些离散点变量值之间关系的代数方程（称为离散方程）。

求解所建立起来的代数方程已获得求解变量的近似值。

数值传热学常用的数值方法1.有限差分法历史上最早采用的数值方法，对简单几何形状中的流动与换热问题最容易实施的数值方法。

其基本点是：将求解区域中用于坐标轴平行的一系列网格的交点所组成的点的集合来代替，在每个节点上，将控制方程中每一个导数用相应的差分表达式来代替，从而在每个节点上，形成一个代数方程，每个方程中包括了本节点及其附近一些节点上的未知值，求解这些代数方程就获得了所需的数值解。

2.有限容积法将所计算的区域划分成一系列控制容积划分为一系列控制容积，每个控制容积都有一个节点做代表。

通过将守恒型的控制方程对控制容积坐积分导出离散方程。

在导出过程中，需要对界面上的被求函数本身及其一阶导数的构成做出假定，是目前流动与换热问题的数值计算中应用最广的一种方法。

3.有限元法把计算区域划分为一系列原题（在二维情况下，元体多为三角形或四边形），由每个元体上去数个点作为节点，然后通过对控制方程做积分来获得离散方程。

数值传热学数值传热学是一门研究如何采用计算机技术模拟传热过程的学科。

它的出现，使得传热学在进行理论分析和数值计算方面更加具有实际意义。

以前要进行传热问题的求解，需要有丰富经验的工程师去积累相应的数据，而且也只能做到相对比较好的效果，这对于我们来说也并非难事，但是就目前情况来看，人工建立一个数值模型对于复杂的传热过程进行求解将会变得更加困难。

而且传统的工业过程模拟中大多都是依靠经验，但是这种经验往往又是片面的、偶然的。

因此，建立一个完整的数值传热学体系就成了当务之急。

然而数值传热学作为一门年轻的学科，它的许多思想都源于传热学的实际应用。

因此，对于传热学基础理论知识的掌握以及综合应用能力的培养对于该课程学习至关重要。

在教学过程中，除了注重学生自身素质的培养外，还应该结合教学内容，创新教学方法，在充分调动学生主观能动性的基础上，发挥他们的创造性思维，让学生参与其中。

另外，还可以借助多媒体教学等现代化教学手段，提高课堂效率，增强教学效果。

从而促进学生对于课程的理解，提升教学质量。

传统的传热学模型很难完全适用于现代化传热分析与设计。

针对于传热模型方面，首先，需要增加数值传热学模型，在原有的基础上引入新的概念和规则；其次，模型的编制需要精确考虑每一个单元模块之间的关联，在保证各个模块都能够单独准确地计算出结果的同时，还必须将他们联系起来。

例如，对于燃烧室内传热问题，由于温度的分布情况是非常复杂的，因此我们需要构造适当的网格进行相应的计算，将所有网格划分成细小的区域，再逐步地建立起燃烧室内温度场的整体结构，进而达到一个有效的、清晰的计算结果。

除此之外，计算结果的收敛速度和计算的精确度也是影响分析效率的两个主要因素。

但是随着对于这些相关领域研究人员的不断增多，一些技术已经可以得到大幅度的改善，甚至部分可以直接用于商业用途。

而计算流体力学（ CFD）就是在计算机运算能力不断增强的基础上逐渐形成的一门新兴学科，它可以通过在计算机上建立一些专门的数学模型，利用计算机仿真软件进行求解，最终获取相应的物理图像或者曲线，帮助工程师快速地找到解决方案。

数值传热学（Numerical Heat Transfer,NHT）又称计算传热学(Computational Heat Transfer,CHT)，是指对描写流动与传热问题的控制方程采用数值方法，通过计算机求解的一门传热学与数值方法相结合的交叉学科。

数值传热学的基本思想是把原来在空间与时间坐标中连续的物理量的场（如速度场，温度场，浓度场等），用一系列有限个离散点(称为节点)上的值的集合来代替，通过一定的原则建立起这些离散点变量值之间关系的代数方程（称为离散方程，discretization equation）,求解所建立起来的代数方程已获得求解变量的近似值。

一、数值传热学的研究作用与地位数值传热学在最近20年中得到飞速的发展，除了计算机硬件工业的发展给它提供了坚实的物质基础外，还主要因为无论分析的方法或实验的方法都有较大的限制，例如由于问题的复杂性，既无法做分析解，也因费用的昂贵而无力进行实验测定，而数值计算的方法正具有成本较低和能模拟复杂或较理想的过程等优点。

经过一定考核的数值计算软件可以拓宽实验研究的范围，减少成本昂贵的实验工作量。

在给定的参数下用计算机对现象进行一次数值模拟相当于进行一次数值实验，历史上也曾有过首先由数值模拟发现新现象而后由实验予以证实的例子。

在这里要指出对数值模拟结果准确度应持正确认识。

计算机本身不能创造信息，发现规律，它只是把人们送入的信息按照计算者所选定的规律进行处理，加工而已。

但一旦建立了实际问题合理的数学模型，数值模拟又能发挥很大的作用。

由于它本身的一些固定优点，它以发展成为工业界进行CAD/CAM及过程控制的重要手段,在多种工程领域中得到广泛应用。

例如：叶轮机器粘性三元流体的计算，电站锅炉炉堂内流场与温度场的模拟；大型初见凝固过程中温度场的预测；单晶拉制过程中温度场及磁场作用的分析；电子器件冷却过程中最高温的预算；换热器可测流场与温度场的三维仿真等。

在这段时间内，用于传热与流动数值模拟的商业软件市场也有了很大的发展，先后出现了一批像PHOENICS,FLUENT,STAR-CD,CFX,FLOW-3D等大型通用软件。