最新北师大版九年级数学下册3.3垂径定理公开课优质教案 (2)

在教学过程中，我注重引导学生从实际问题出发，通过观察和操作，发现垂径定理的内在规律。我设计了一系列的教学活动，包括直观演示、小组讨论、几何画板软件操作等，旨在激发学生的学习兴趣，提高学生的参与度。
同时，我还注重培养学生的逻辑思维能力，引导学生从特殊到一般，从具体到抽象的思考问题，让学生在理解垂径定理的同时，能够灵活运用该定理解决实际问题。
（三）学生小组讨论
1.设计具有挑战性和综合性的小组合作任务，让学生在合作中思考、交流、探究，提高学生的学习效果。
2.组织学生进行小组讨论，鼓励学生提出问题、分享思路、互相启发、互相学习，培养学生的批判性思维和问题解决能力。
3.教师在小组讨论过程中给予及时的反馈和指导，帮助学生更好地理解和掌握垂径定理。
（四）反思与评价
1.引导学生对学习过程进行反思，培养学生自我评价和自我调整的能力。
2.设计具有针对性和全面性的评价指标体系，对学生的知识与技能、过程与方法、情感态度与价值观进行全面评价。
3.利用自评、互评、师评等多种评价方式，给予学生客观、公正的评价，提高学生的自信心和积极性。
4.根据评价结果，调整教学策略和教学方法，为下一阶段的教学提供有益的参考。
北师大版九年级下册3.3垂径定理优秀教学案例
一、案例背景
北师大版九年级下册3.3垂径定理是圆的知识点中的一个重要定理，它揭示了圆中关于垂直于弦的直径的一系列性质。在本节课中，学生需要理解和掌握垂径定理的内容，并能够运用该定理解决相关问题。
在进行本节课的教学设计时，我充分考虑了学生的年龄特点和学习需求，以提高学生的几何思维能力和解决问题的能力为目标，力求通过丰富的教学活动和合理的教学设计，帮助学生理解和掌握垂径定理。
2.要求学生对自己的作业进行自我评价，培养学生的自我反思和自我调整能力。

1.概念讲解：明确垂径定理的定义，即圆的直径垂直于弦，并且平分弦。
2.证明过程：引导学生通过几何画板或实际操作，观察并思考如何证明垂径定理。在此基础上，给出严格的证明过程，强调证明方法与逻辑推理。
3.推论介绍：介绍垂径定理的两个重要推论，即弦的一半、弦心距和圆半径构成直角三角形，以及圆的弦垂直平分线相交于圆心。
4.通过对垂径定理及其推论的学习，使学生体会几何知识之间的联系，培养他们运用几何知识解决实际问题的能力。
（三）情感态度与价值观
1.激发学生对几何学的兴趣，培养他们主动探究、积极思考的学习态度。
2.通过对垂径定理的学习，使学生体会数学的简洁美和逻辑美，提高他们对数学的审美能力。
3.培养学生的团队合作精神，使他们学会在合作中交流、分享和互助，共同解决问题。
3.情感态度培养：鼓励学生勇于提出问题、发表见解，培养他们的自信心和批判性思维。
4.课后作业布置：布置适量的课后作业，让学生巩固所学知识，为下一节课的学习打下基础。
五、作业布置
为了巩固学生对垂径定理的理解和应用，以及培养学生的独立思考能力，特布置以下作业：
1.基础巩固题：请同学们完成课本第63页的练习题1、2、3，这些题目主要考察对垂径定理基本概念的理解和简单应用。
5.请同学们按时提交作业，教师将及时批改、反馈，帮助大家查漏补缺，提高学习效果。
2.教学难点：垂径定理的证明过程，以及在实际问题中的应用。
-证明过程涉及严密的逻辑推理，对于部分学生来说可能存在理解上的困难。
-在实际应用中，学生需要能够灵活运用定理，结合其他几何知识，解决更为复杂的问题。
（二）教学设想
1.采定理及其推论。
-教师应以鼓励和表扬为主，营造积极向上的课堂氛围，让学生在轻松的环境中学习。

弦，观察一下，还有与刚才类似的结论吗？
C
AE=BE， AC=BC，AD=BD
A
O E
B
D
探索新知——垂径定理及其逆定理
活动：
在圆纸片上画出图形，并沿CD折叠，实验后提出
猜想.
C
猜想：垂直于弦的直径
平分这条弦，并且平分弦所
O
对的弧.
E
A
B
D
你能写出已知求 证，并证明吗？
探索新知——垂径定理及其逆定理
别相等.
A M
B
O
B′ M′ A′
探索新知——垂径定理及其逆定理
（1）在探索圆的轴对称性的过程中，若沿两条直径 折叠可以是哪些位置关系呢？ 斜交，垂直
垂直是特殊情况，你能得出哪些等量关系？
C
A
B
O
D
AO=BO，CO=DO，AC=BC，AD=BD
探索新知——垂径定理及其逆定理
（2）若把AB向下平移到任意位置，变成非直径的
直径，并且CD⊥AB ，垂足为M.
C
求证：AE=BE， AC=BC， AD=BD.
若只证明AE=BE，还有什么方
A
法？
O E
B D
探索新知——垂径定理及其逆定理
猜想得以证明，命题是真命题，我们把真命题叫 做____定___理____.
垂径定理：垂直于弦的直径平分这条弦，并且平 分弦所对的弧.
垂径定理的推理格式
弓形CED.
弓形的高：从圆心向弦作垂 线,垂线被弦和弧所截的线段的长,
称为弓形的高.如EF .
C E
FD
O
应用实际
例2.已知：如图，在以O为圆心的两个同心圆中， 大圆的弦AB交小圆于C，D两点.

垂径定理一、教学目标1．利用圆的轴对称性研究垂径定理及其逆定理； 2．运用垂径定理及其逆定理解决问题． 二、教学重点和难点重点：利用圆的轴对称性研究垂径定理及其逆定理．难点：垂径定理及其逆定理的证明，以及应用时如何添加辅助线 三、教学过程 （一）情境引入：1．如图，AB 是⊙O 的一条弦，作直径CD ，使CD ⊥AB ，垂足为M ． （1）该图是轴对称图形吗？如果是，其对称轴是什么？ （2）你能图中有哪些等量关系？（3）你能给出几何证明吗？（写出已知、求证并证明）（二）知识探究：【探究一】通过上面的证明过程，我们可以得到：1.垂径定理_____________________________________________________2.注意：①条件中的“弦”可以是直径；②结论中的“平分弧”指平分弦所对的劣弧、优弧。

③定理中的两个条件缺一不可——______________，______________． 3.给出几何语言如图，已知在⊙O 中，AB 是弦，CD 是直径，如果CD ⊥AB,垂足为E, 那么AE=_______,⋂AC =______,⋂BD =________4．辨析：判断下列图形，能否使用垂径定理？1.，作一条平分AB于点M .（1）下图是轴对称图形吗？如果是，其对称轴是什么？ （2）图中有哪些等量关系？说一说你的理由.2.垂径定理的推论：______________________________________________________________ 3．辨析：“平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧．”如果该定理 少了“不是直径”，是否也能成立？ 反例：4.如图，在⊙O 中，AB 是弦（不是直径），CD 是直径， （1）如果AE=BE 那么CD____AB,⋂AC =____⋂BD =____ (2)如果⋂AC =⋂BC 那么CD____AB ，AE______BE ，⋂BD =____ （3）如果⋂AD =⋂BD 那么CD____AB ，AE_____BE ，⋂AC =______ （三）典例讲解：1．例：如图，一条公路的转弯处是一段圆弧（即图中⌒CD ,点0是⌒CD 所在圆的圆心），其中CD =600m ，E 为⌒CD 上的一点，且OE ⊥CD ，垂足为F ，EF =90m.求这段弯路的半径．2.如果圆的两条弦互相平行，那么这两条弦所夹的弧相等吗？为什么？（四）巩固训练： 题组一1.如图，在⊙O 中，AB 为弦，OC ⊥AB 于C ，若AO=5,OC=3,求弦AB 的长。

第三章圆3、垂径定理（1）一、学生学情分析学生的知识技能基础：学生在小学时已经学习过圆的概念，对圆有一定的认识。

本章又学习了圆有关的概念，这些都为这一节课的学习做好了铺垫。

圆的垂径定理是这一节的关键，为圆有关的计算证明都起到重要的作用。

本期我担任两个班级，9（1、2）.学生基础水平较差，因此在备课方面就要班级学生的差异性进行备课，难度较大。

练习以及作业的布置方面也有所不同，总之为了上好本课时在各个方面都必须下足功夫。

二、教学任务分析垂径定理是初中最重要的定理之一，关系到圆有关的计算及证明。

教学目标：【知识与技能】1、进一步认识圆，了解圆是轴对称图形.2、理解垂直于弦的直径的性质和推论，并能应用它解决一些简单的计算、证明。

【过程与方法】经历探索垂径定理的过程，培养学生类比的思想及发展有条理的思考及其语言表达能力.【情感态度与价值观】①通过学习垂径定理定理，理解事物拓延的内在本质，丰富数学情感与思想。

②结合已有的数学经验，解决新问题，获得成就感以及克服困难的方法和勇气.教学重、难点【重点】：垂径定理的理解及应用。

【难点】：理解垂径定理及其推论，并能应用它解决一些简单的计算、证明。

【关键点】理解并应用垂径定理。

三、教学过程设计本节课设计了6个教学环节：情景引入——讲授新课——典例精析——课堂练习——课堂小结——布置作业第一环节情景引入问题:你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵州桥主桥拱的半径吗？第二环节讲授新课垂径定理及其推论问题：如图,AB是⊙O的一条弦, 直径CD⊥AB, 垂足为P.你能发现图中有哪些相等的线段和劣弧? 为什么?通过分析归纳得出垂径定理：垂直于弦的直径平分这条弦,并且平分弦所对的弧.垂径定理的推论：平分弦（不是直径）的直径垂直于弦,并且平分弦所对的弧.温馨提示：垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.第三环节典例精析例1、如图，OE⊥AB于E，若⊙O的半径为10cm,OE=6cm,则AB= （）cm.分析：例2如图，一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD，垂足为F,EF=90m.求这段弯路的半径.分析：第四环节课堂练习1、如图，⊙O的弦AB＝8cm ，直径CE⊥AB于D，DC＝2cm，求半径OC的长.2、如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．3、已知：⊙O中弦AB∥CD,求证：AC＝BD.4、已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。

2024北师大版数学九年级下册3.3《垂径定理》教学设计一. 教材分析《垂径定理》是北师大版数学九年级下册第3.3节的内容，本节课主要介绍垂径定理及其应用。

垂径定理是指：圆中，如果一条直径垂直于一条弦，那么这条直径把这条弦平分。

这个定理是圆的基本性质之一，对于解决与圆有关的问题具有重要意义。

二. 学情分析学生在学习本节课之前，已经掌握了圆的基本概念、性质以及一些基本的运算。

但是，对于证明一个定理，他们可能还不是很熟悉。

因此，在教学过程中，需要引导学生通过观察、思考、推理等方法，逐步理解并证明垂径定理。

三. 教学目标1.理解垂径定理的内容，并掌握其证明过程。

2.能够运用垂径定理解决与圆有关的问题。

3.培养学生的观察能力、思考能力和推理能力。

四. 教学重难点1.教学重点：垂径定理的内容及其证明过程。

2.教学难点：如何引导学生通过观察、思考、推理等方法，证明垂径定理。

五. 教学方法1.引导法：通过提问、引导，激发学生的思考，帮助他们理解垂径定理。

2.推理法：引导学生通过观察、推理，证明垂径定理。

3.实例法：通过具体的例子，让学生学会如何运用垂径定理解决实际问题。

六. 教学准备1.教学PPT：包括垂径定理的定义、证明过程以及应用实例。

2.教学素材：一些与圆有关的问题，用于巩固和拓展学生的知识。

3.黑板：用于板书重要的概念和证明过程。

七. 教学过程1.导入（5分钟）通过一个简单的与圆有关的问题，引导学生复习之前学过的知识，为新课的学习做好铺垫。

2.呈现（10分钟）介绍垂径定理的定义和证明过程。

首先，让学生观察一些与圆有关的几何图形，引导他们发现其中的规律。

然后，通过推理和论证，得出垂径定理的结论。

3.操练（10分钟）让学生分组讨论，尝试用垂径定理解决一些与圆有关的问题。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）针对学生的讨论结果，进行讲解和分析，巩固他们对垂径定理的理解。

同时，通过一些具体的例子，让学生学会如何运用垂径定理解决实际问题。

北师大版九年级数学下册：3.3《垂径定理》教学设计一. 教材分析《垂径定理》是北师大版九年级数学下册第3章第3节的内容。

本节主要介绍圆中的垂径定理及其应用。

垂径定理是圆的基本性质之一，对于解决与圆相关的问题具有重要意义。

通过学习垂径定理，学生能够更深入地理解圆的性质，提高解决实际问题的能力。

二. 学情分析九年级的学生已经掌握了圆的基本概念和性质，具备了一定的观察、分析和推理能力。

但在学习垂径定理时，学生可能对定理的理解和应用还存在一定的困难。

因此，在教学过程中，教师需要关注学生的认知水平，引导学生逐步理解并掌握垂径定理。

三. 教学目标1.理解垂径定理的内容及证明过程。

2.能够运用垂径定理解决与圆相关的问题。

3.培养学生的观察能力、推理能力和解决问题的能力。

四. 教学重难点1.重点：垂径定理的理解和应用。

2.难点：垂径定理的证明过程。

五. 教学方法1.引导发现法：教师引导学生观察、分析、推理，发现垂径定理。

2.实例讲解法：教师通过具体例子，讲解垂径定理的应用。

3.合作交流法：学生分组讨论，分享学习心得和解决问题的方法。

六. 教学准备1.教学PPT：包含垂径定理的定义、证明和应用。

2.实例图片：用于讲解垂径定理的应用。

3.练习题：巩固所学内容。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾圆的基本性质，为新课的学习做好铺垫。

2.呈现（10分钟）教师展示PPT，介绍垂径定理的定义、证明和应用。

引导学生观察、分析，理解垂径定理的意义。

3.操练（10分钟）教师提出几个与垂径定理相关的问题，让学生分组讨论，共同解决问题。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）学生独立完成几道练习题，巩固所学内容。

教师选取部分题目进行讲解，分析解题思路。

5.拓展（10分钟）教师提出一些拓展问题，引导学生运用垂径定理解决实际问题。

学生分组讨论，分享解题方法。

6.小结（5分钟）教师引导学生总结本节课所学内容，回顾学习过程，分享学习心得。

垂径定理公开课优秀教案一、教学目标1. 知识与技能：（1）让学生掌握垂径定理的内容及应用；（2）培养学生运用几何知识解决实际问题的能力。

2. 过程与方法：（1）通过观察、实验、证明等环节，引导学生发现并证明垂径定理；（2）运用垂径定理解决一些相关的几何问题。

3. 情感态度与价值观：（1）培养学生对数学的兴趣和自信心；（2）培养学生合作交流、归纳总结的能力。

二、教学重点与难点1. 教学重点：（1）垂径定理的内容及其应用；（2）运用垂径定理解决一些相关的几何问题。

2. 教学难点：（1）垂径定理的证明；（2）在实际问题中灵活运用垂径定理。

三、教学方法1. 采用问题驱动法，引导学生发现并证明垂径定理；2. 运用几何画板软件，直观展示垂径定理的应用；3. 设计具有梯度的练习题，巩固学生对垂径定理的理解。

四、教学准备1. 教师准备：垂径定理的相关知识、课件、练习题；2. 学生准备：笔记本、几何画板软件。

五、教学过程1. 导入新课（1）复习相关知识：圆的基本概念、圆的性质；（2）提问：如何判断一条直线是否垂直于一条弦？2. 探究与发现（1）学生分组讨论，尝试发现垂径定理；（2）各组汇报讨论成果，师生共同总结垂径定理；（3）教师利用几何画板软件，演示垂径定理的应用。

3. 证明垂径定理（1）学生根据已知的圆的性质，尝试证明垂径定理；（2）教师引导学生归纳总结，给出垂径定理的证明过程。

4. 应用垂径定理（1）设计一组练习题，让学生运用垂径定理解决问题；（2）学生独立解答，教师点评并指导。

5. 课堂小结（1）学生总结本节课所学内容；（2）教师补充，强调垂径定理在几何中的应用。

6. 作业布置（1）请学生运用垂径定理解决一些实际问题；（2）复习本节课所学知识，为下一节课做准备。

六、教学拓展1. 引导学生思考：垂径定理在实际生活中的应用有哪些？2. 举例说明：如在建筑设计中，如何利用垂径定理确定圆形的建筑物的垂直结构。

七、课堂互动1. 学生之间互相提问关于垂径定理的问题，加深对知识的理解；2. 教师参与互动，解答学生提出的问题，及时纠正学生的错误。

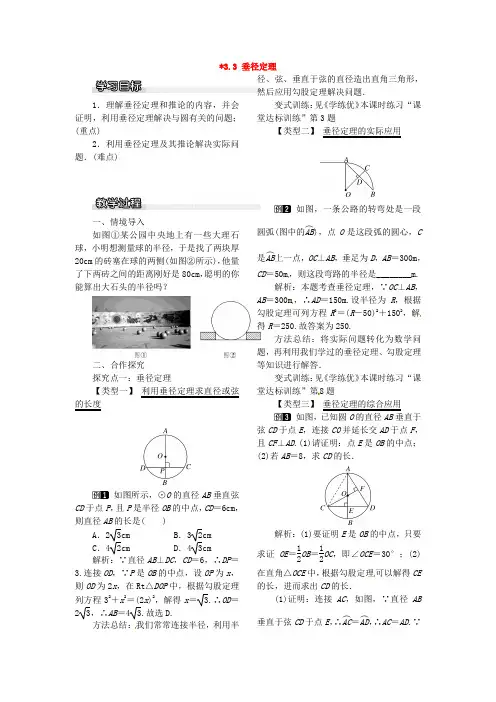
*3.3 垂径定理1．理解垂径定理和推论的内容，并会证明，利用垂径定理解决与圆有关的问题；(重点)2．利用垂径定理及其推论解决实际问题．(难点)一、情境导入如图①某公园中央地上有一些大理石球，小明想测量球的半径，于是找了两块厚20cm的砖塞在球的两侧(如图②所示)，他量了下两砖之间的距离刚好是80cm，聪明的你能算出大石头的半径吗？二、合作探究探究点一：垂径定理【类型一】利用垂径定理求直径或弦的长度如图所示，⊙O的直径AB垂直弦CD于点P，且P是半径OB的中点，CD＝6cm，则直径AB的长是( )A．23cm B．32cmC．42cm D．43cm解析：∵直径AB⊥DC，CD＝6，∴DP＝3.连接OD，∵P是OB的中点，设OP为x，则OD为2x，在Rt△DOP中，根据勾股定理列方程32＋x2＝(2x)2，解得x＝ 3.∴OD＝23，∴AB＝4 3.故选D.方法总结：我们常常连接半径，利用半径、弦、垂直于弦的直径造出直角三角形，然后应用勾股定理解决问题．变式训练：见《学练优》本课时练习“课堂达标训练”第3题【类型二】垂径定理的实际应用如图，一条公路的转弯处是一段圆弧(图中的AB︵)，点O是这段弧的圆心，C 是AB︵上一点，OC⊥AB，垂足为D，AB＝300m，CD＝50m，则这段弯路的半径是________m.解析：本题考查垂径定理，∵OC⊥AB，AB＝300m，∴AD＝150m.设半径为R，根据勾股定理可列方程R2＝(R－50)2＋1502，解得R＝250.故答案为250.方法总结：将实际问题转化为数学问题，再利用我们学过的垂径定理、勾股定理等知识进行解答．变式训练：见《学练优》本课时练习“课堂达标训练”第8题【类型三】垂径定理的综合应用如图，已知圆O的直径AB垂直于弦CD于点E，连接CO并延长交AD于点F，且CF⊥AD.(1)请证明：点E是OB的中点；(2)若AB＝8，求CD的长．解析：(1)要证明E是OB的中点，只要求证OE＝12OB＝12OC，即∠OCE＝30°；(2)在直角△OCE中，根据勾股定理可以解得CE 的长，进而求出CD的长．(1)证明：连接AC，如图，∵直径AB 垂直于弦CD于点E，∴AC︵＝AD︵，∴AC＝AD.∵过圆心O 的直线CF ⊥A D ，∴AF ＝DF ，即CF 是AD 的垂直平分线，∴AC ＝CD ，∴AC ＝AD ＝CD ，即△ACD 是等边三角形，∴∠FCD ＝30°.在Rt △COE 中，OE ＝12OC ，∴OE ＝12OB ，∴点E 为OB 的中点；(2)解：在Rt △OCE 中，AB ＝8，∴OC ＝OB ＝12AB ＝4.又∵BE ＝OE ，∴OE ＝2，∴CE＝OC 2－OE 2＝16－4＝23，∴CD ＝2CE ＝4 3.方法总结：解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里，运用勾股定理求解．变式训练：见《学练优》本课时练习“课后巩固提升”第5题探究点二：垂径定理的推论【类型一】 利用垂径定理的推论求角的度数如图所示，⊙O 的弦AB 、AC 的夹角为50°，M 、N 分别是AB ︵、AC ︵的中点，则∠MON 的度数是( )A ．100°B ．110°C ．120°D ．130°解析：已知M 、N 分别是AB ︵、AC ︵的中点，由“平分弧的直径垂直平分弧所对的弦”得OM ⊥AB 、ON ⊥AC ，所以∠AEO ＝∠AFO ＝90°，而∠BAC ＝50°，由四边形内角和定理得∠MON ＝360°－∠AEO －∠AFO －∠BAC ＝360°－90°－90°－50°＝130°.故选D.变式训练：见《学练优》本课时练习“课堂达标训练”第6题．【类型二】 利用垂径定理的推论求边的长度如图，点A 、B 是⊙O 上两点，AB＝10cm ，点P 是⊙O 上的动点(与A 、B 不重合)，连接AP 、BP ，过点O 分别作OE ⊥AP 于E ，OF ⊥PB 于F ，求EF 的长．解析：运用垂径定理先证出EF 是△ABP 的中位线，然后运用三角形中位线性质把要求的EF 与AB 建立关系，从而解决问题．解：在⊙O 中，∵OE ⊥AP ，OF ⊥PB ，∴AE ＝PE ，BF ＝PF ，∴EF 是△ABP 的中位线，∴EF ＝12AB ＝12×10＝5(cm)．方法总结：垂径定理虽是圆的知识，但也不是孤立的，它常和三角形等知识综合来解决问题，我们一定要把知识融会贯通，在解决问题时才能得心应手．变式训练：见《学练优》本课时练习“课后巩固提升”第2题【类型三】 动点问题如图，⊙O 的直径为10cm ，弦AB＝8cm ，P 是弦AB 上的一个动点，求OP 的长度范围．解析：当点P 处于弦AB 的端点时，OP 最长，此时OP 为半径的长；当OP ⊥AB 时，OP 最短，利用垂径定理及勾股定理可求得此时OP 的长．解：作直径MN ⊥弦AB ，交AB 于点D ，由垂径定理，得AD ＝DB ＝12AB ＝4cm.又∵⊙O的直径为10cm ，连接OA ，∴OA ＝5cm.在Rt △AOD 中，由勾股定理，得OD ＝OA 2－AD 2＝3cm.∵垂线段最短，半径最长，∴OP 的长度范围是3cm ≤OP ≤5cm.方法总结：解题的关键是明确OP 最长、最短时的情况，灵活利用垂径定理求解．容易出错的地方是不能确定最值时的情况．三、板书设计垂径定理1．垂径定理2．垂径定理的推论垂径定理是中学数学中的一个很重要的定理，由于它涉及的条件结论比较多，学生容易搞混淆，本节课采取了讲练结合、动手操作的教学方法，课前布置所有同学制作一张圆形纸片，课上利用此纸片探索、体验圆是轴对称图形，并进一步利用圆的轴对称性探究垂径定理，环环相扣、逐层深入，激发学生的学习兴趣，收到了很好的教学效果.3.3垂径定理一、教学目标1.通过手脑结合，充分掌握圆的轴对称性.2.运用探索、推理，充分把握圆中的垂径定理及其逆定理.3.拓展思维，与实践相结合，运用垂径定理及其逆定理进行有关的计算和证明.二、课时安排1课时三、教学重点运用探索、推理，充分把握圆中的垂径定理及其逆定理.四、教学难点运用垂径定理及其逆定理进行有关的计算和证明.五、教学过程（一）导入新课引导学生说出点与圆的位置关系：（二）讲授新课活动内容1：探究1：圆的相关概念——弧、弦、直径1.圆上任意两点间的部分叫做圆弧，简称弧.２.连接圆上任意两点的线段叫做弦.３.经过圆心的弦叫做直径探究2： AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M. 你能发现图中有哪些等量关系?与同伴说说你的想法和理由.小明发现图中有:理由：连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB，OM=OM，∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B 重合,AC BC,AD BD.和重合和重合AC BC,AD BD.∴==活动2：探究归纳定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

3.重点难点解析：在讲授过程中，我会特别强调垂径定理的定义及其证明过程这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与垂径定理相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作。这个操作将演示垂径定理的基本原理。
5.培养学生养成良好的学习习惯，提高自主学习、探究学习的能力，形成终身学习的观念。
三、教学难点与重点
1.教学重点
-理解垂径定理的概念：垂径定理是圆的基本性质之一，对于圆的认识具有重要意义。教学过程中应重点讲解垂径定理的定义，使学生明确垂直于弦的直径平分弦，并且平分弦所对的两条弧。
-掌握垂径定理的证明方法：通过运用勾股定理和圆周角定理，引导学生理解并掌握垂径定理的证明过程，培养学生严谨的逻辑推理能力。
此外，在总结回顾环节，学生们能够较好地掌握垂径定理的基本概念和应用。但我也注意到，部分学生在提问环节显得较为拘况，我将在课堂上鼓励学生大胆提问，充分表达自己的观点，同时给予他们更多的肯定和鼓励。
最后，针对本节课的教学，我认为以下方面需要改进：
a.引导学生观察图形，发现垂径定理的规律。
b.分步骤解释证明过程，强调勾股定理和圆周角定理的应用。
c.通过提问和互动，了解学生在证明过程中遇到的难点，并针对性地进行解答。
d.组织学生进行小组讨论，共同解决证明过程中的问题，培养学生的团队合作能力。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《垂径定理》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要找到圆中某个点，使得从这个点到圆周上某点的距离最短的情况？”（例如：如何在一张纸上剪出一个最大的圆）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索垂径定理的奥秘。

3.3 垂径定理 教学设计 2023--2024学年北师大版九年级数学下册
课题：
科目：
班级：
课时：计划1课时
教师：
单位：
一、教学内容分析
1. 本节课的主要教学内容为“垂径定理”。教学内容选自2023--2024学年北师大版九年级数学下册第3章第3节，主要包括垂径定理的定义、性质及其应用。
2. 教学内容与学生已有知识的联系：学生在八年级已经学习了圆的性质、圆的方程以及圆的切线，对圆的基本概念有了较为深入的理解。在此基础上，本节课将引导学生探索垂径定理，使学生进一步掌握圆的性质，并为后续学习圆的弦、弧等相关知识奠定基础。通过本节课的学习，学生将能更好地理解圆的相关性质，提高解决问题的能力。
3. 学生在学习垂径定理过程中可能遇到的困难和挑战有：理解并掌握垂径定理的证明过程，将定理应用于解决具体问题，特别是在涉及多步骤、综合性的几何问题时，可能会感到困惑。此外，对定理的灵活运用和拓展也可能会给学生带来挑战。
四、教学方法与手段
教学方法：
1. 讲授法：通过讲解垂径定理的定义、性质和证明过程，帮助学生建立清晰的知识体系。
2. 讨论法：组织学生分组讨论垂径定理的应用实例，培养学生的合作意识和解决问题的能力。
3. 实验法：引导学生通过画图、实际测量等实验方式，直观感受垂径定理的成立和运用。
教学手段：
1. 多媒体设备：运用PPT、动画等展示垂径定理的证明过程和应用实例，提高学生的学习兴趣。
2. 教学软件：利用几何画板等教学软件，让学生动手操作，加深对垂径定理的理解。
3. 垂径定理的性质：
a. 圆的直径平分弦，并且垂直于弦。
b. 圆的直径平分弦所对的两条弧。
c. 圆的半径垂直于弦，并且平分弦所对的弧。

三、教学重难点和教学设想
（一）教学重难点
1.重点：理解并掌握垂径定理及其证明过程，能够灵活运用垂径定理解决相关问题。
2.难点：
（1）从具体实例中抽象出垂径定理，理解其几何本质。
（2）运用逻辑推理证明垂径定理，培养学生的逻辑思维和推理能力。
（3）将垂径定理应用于解决与圆相关的实际问题，提高学生的应用能力。
5.小组合作题：安排一道需要团队合作完成的题目，要求学生在小组内部分工合作，共同解决问题。这样的题目有助于提高学生的沟通协作能力，同时也能让学生在合作中发现问题、解决问题。
作业要求：
1.学生需独立完成作业，书写规范，保持卷面整洁。
2.对于提高拓展题和实践应用题，鼓励学生尝试不同的解题方法，注重解题过程的逻辑性和思维的创造性。
为了巩固学生对垂径定理的理解和应用，以及提高他们的数学思维能力，特布置以下作业：
1.基础巩固题：请学生完成课后练习题中与垂径定理相关的前三题，旨在帮高拓展题：选择两道具有一定难度的题目，要求学生在理解垂径定理的基础上，结合其他几何知识，如圆周角定理、相似三角形等，解决问题。这样的题目旨在培养学生的综合解题能力和逻辑思维。
4.教学策略：
（1）注重分层教学，针对不同水平的学生，设计不同难度的教学任务，使每个学生都能在原有基础上得到提高。
（2）鼓励学生积极参与课堂讨论，培养学生的表达和倾听能力。
（3）关注学生的情感态度，营造轻松愉快的学习氛围，激发学生的学习兴趣。
四、教学内容与过程
（一）导入新课
1.复习引入：首先，引导学生复习圆的基本概念，如半径、直径、弦、弧等。通过提问方式，让学生回顾这些概念的定义及性质，为新课的学习打下基础。
3.小组合作题需明确每个成员的责任，确保每个学生都能积极参与，共同完成任务。

课题*3 垂径定理课时1课时上课时间45教学目标1.知识与技能(1)利用圆的轴对称性研究垂径定理及其逆定理.(2)运用垂径定理及其逆定理解决问题.2.过程与方法经历运用圆的轴对称性探索圆的相关性质的过程,进一步体会和理解研究几何图形的各种方法.3.情感、态度与价值观(1)培养学生类比分析,猜想探索的能力.(2)通过学习垂径定理及其逆定理的证明,使学生领会数学的严谨性和探索精神,培养学生实事求是的科学态度和积极参与的主动精神.教学重难点重点:利用圆的轴对称性研究垂径定理及其逆定理.难点:垂径定理及其逆定理的证明,以及应用时如何添加辅助线.教学活动设计二次设计课堂导入提出问题,引入新课:1.等腰三角形是轴对称图形吗?2.如果将一等腰三角形沿底边上的高对折,可以发现什么结论?3.如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?探索新知合作探究自学指导如图,AB是☉O的一条弦,作直径CD,使CD⊥AB,垂足为M.(1)该图是轴对称图形吗?如果是,其对称轴是什么?(2)你能发现图中有哪些等量关系?(3)你能给出几何证明吗?(写出已知、求证并证明)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.合作探究1.小组讨论自学指导中出现疑问的地方.2.如图,AB是☉O的弦(不是直径),作一条平分AB的直径CD,交AB于点M.(1)如图是轴对称图形吗?如果是,其对称轴是什么?(2)图中有哪些等量关系?说一说你的理由.(3)你能模仿垂径定理的证明过程,自行证明逆定理吗?续表探索新知合作探究(4)你能正确表述逆定理的内容吗?(5)“平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.”如果该定理少了“不是直径”,是否也能成立？点拨：条件:①CD是直径;②AM=BM.结论(等量关系):③CD⊥AB;④;⑤.垂径定理逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.学以致用思考如下问题:(1)如何利用所学定理添加辅助线?(2)这样添加辅助线的目的是什么?(3)你想利用直角三角形的什么知识来解决问题?(4)大家能合作完成求解过程吗?点拨(1)垂径定理中的两个条件缺一不可——直径(半径),垂直于弦.(2)垂径定理的逆定理中“不是直径”不可或缺,否则错误.尝试应用：1. (毕节中考)如图，在⊙O中，弦AB的长为8，OC⊥AB，垂足为C，且OC＝3，则⊙O的半径为( )A．5 B．10 C．8 D．61题 2题2. 如图，在⊙O中，直径AB＝4，弦CD⊥AB于P，OP＝3，则弦CD的长为____________．3. 1400年前，我国隋朝建造的赵州石拱桥的桥拱是圆弧形，它的跨度（弧所对的弦长）为37.4米，拱高（即弧的中点到弦的距离）为7.2米，求桥拱所在圆的半径．（结果精确到0.1米）．盘点提升1.学了本节课，你还有什么疑问？2.你的收获？知识：(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.(2)垂径定理逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.方法规律:解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连接半径等辅助线,为应用垂径定理创造条件.当堂达标1. 如图，⊙O的半径为5，AB为弦，半径OC⊥AB，垂足为点E，若OE=3，则AB的长是（）A．4 B．6 C．8 D．101题 2题 3题 4题2. 如图，圆O过点A、B，圆心O在正△ABC的内部，AB=2，OC=1，则圆O的半径为（）A．B．2 C．D．3.如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是（）A．3≤OM≤5 B．4≤OM≤5 C．3＜OM＜5 D．4＜OM＜54.如图，CD是⊙O的直径，弦AB⊥CD于点H，若∠D=30°，CH=1cm，则AB= cm．5.如图，MN是⊙O的直径，矩形ABCD的顶点A、D在MN上，顶点B、C在⊙O 上，若⊙O的半径为5，AB=4，则AD边的长为．5题 6题6. 如图所示，⊙O内有折线OABC，其中OA=2，AB=4，∠A=∠B=60°，则BC的长为．7．如图，⊙O的半径为2，弦AB=2，点C在弦AB上，AC=AB，求OC的长．智者加速8. 如图，⊙O的半径为10cm，弦AB∥CD，AB=16cm，CD=12cm，圆心O位于AB、CD的上方，求AB和CD间的距离．9．如图，一个宽为2cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），求该光盘的直径是多少？10．今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何．（选自《九章算术》卷第九“句股”中的第九题，1尺=10寸）．板书设计垂径定理1.垂径定理 3.例题2.垂径定理的逆定理。

垂径定理垂径定理的应用一、教学目标运用垂径定理及其逆定理解决问题．二、教学重点和难点重点：运用垂径定理及其逆定理解决问题．难点：运用垂径定理及其逆定理解决问题，以及应用时如何添加辅助线三、教学过程（一）复习回顾：1. 复述垂径定理和推论垂径定理_____________________________________________________垂径定理的推论：______________________________________________________________2.概念辨析：①垂直于弦的直线平分这条弦，并且平分弦所对的两条弧. （）②平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧.（）③经过弦的中点的直径一定垂直于弦. （）④圆的两条平行弦所夹的弧相等. （）⑤弦的垂直平分线一定平分这条弦所对的弧. （）（二）典型例题例1. 如图,一条公路的转弯处是一段圆弧,点O是这段弧的圆心,AB=300m,C是弧AB上一点,OC⊥AB,垂足为D,CD=45, 求这段弯路的半径。

解：连接OA例2：如图是两个同心圆，AB是大圆的弦，与小圆交于C、D两点，则AC=BD试说明理由例3：如图，直径AB与弦CD交于E点，且E是CD中点，CD=8, AE=2,求直径AB（三）、课堂练习：1.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示，已知AB=16m，半径OA=10m，则中间柱CD的高度为多少米？2.在直径为1000mm的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB=800mm，则油的最大深度为多少mm？3.如图，某花园小区一圆形管道破裂，修理工准备更换一段新管道，现在量得污水水面宽度为80cm，水面到管道顶部距离为20cm，则修理工应准备内直径是多少 cm的管道？4.如图是一单位拟建的大门示意图，上部是一段直径为10米的圆弧形，下部是矩形ABCD，其中AB=3.7米，BC=6米，则弧AD的中点到BC的距离是多少米？5. 一跨河桥，桥拱是圆弧形，跨度(AB)为16米，拱高(CD)为4米，求：⑴桥拱半径⑵若大雨过后，桥下河面宽度(EF)为12米，求水面涨高了多少？中国书法艺术说课教案今天我要说课的题目是中国书法艺术，下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。

3.3垂径定理一、教学目标1.通过手脑结合，充分掌握圆的轴对称性.2.运用探索、推理，充分把握圆中的垂径定理及其逆定理.3.拓展思维，与实践相结合，运用垂径定理及其逆定理进行有关的计算和证明.二、课时安排1课时三、教学重点运用探索、推理，充分把握圆中的垂径定理及其逆定理.四、教学难点运用垂径定理及其逆定理进行有关的计算和证明.五、教学过程（一）导入新课引导学生说出点与圆的位置关系：（二）讲授新课活动内容1：探究1：圆的相关概念——弧、弦、直径1.圆上任意两点间的部分叫做圆弧，简称弧.２.连接圆上任意两点的线段叫做弦.３.经过圆心的弦叫做直径探究2： AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M. 你能发现图中有哪些等量关系?与同伴说说你的想法和理由.小明发现图中有:理由：连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB，OM=OM，∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,和重合和重合AC BC,AD BD.∴==AC BC,AD BD.活动2：探究归纳定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧.ODCBA（三）重难点精讲例1.如图，在⊙O 中，CD 是直径，AB 是弦，且CD⊥AB，已知CD = 20，CM = 4，求AB.ODCBAM证明：连接OA ，∵ CD = 20，∴ AO = CO = 10. ∴ OM = OC – CM = 10 – 4 = 6. 在⊙O 中，直径CD ⊥AB ， ∴ AB =2AM ， △OMA 是直角三角形.在Rt △OMA 中，AO = 10，OM = 6， 根据勾股定理，得：222AO OM AM =+，2222AM AO OM 1068=-=-=， ∴ AB = 2AM = 2 × 8 = 16.例2.如图，两个圆都以点O 为圆心，小圆的弦CD 与大圆的弦AB 在同一条直线上.你认为AC 与BD 的大小有什么关系？为什么？解:作OG ⊥AB ， ∵AG=BG,CG=DG ， ∴AC=BD.例3.如图,一条公路的转弯处是一段圆弧(即图中CD ,点O 是CD 所在圆的圆心),其中CD=600m,E 是CD 上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.CE FDO解:连接OC.,(90).Rm OF R m =-设弯路的半径为则,OE CD ⊥11600300().22CF CD m ∴==⨯= 根据勾股定理得：222,OC CF OF =+即()22230090.R R =+-解这个方程得R=545∴这段弯路的半径为545米。

3.3 垂径定理教学设计1.通过圆的轴对称性质的学习，理解垂径定理及其推论.(重点).2.能运用垂径定理及其推论计算和解决实际问题.(难点)提出问题 ：你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶．它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m ，你能求出赵洲桥主桥拱的半径吗？阅读教材P 74～75，完成预习内容.（掌握好时间）(一)知识探究（图形，几何语言的描述）1.垂直于弦的直径平分这条弦，并且平分弦所对的两条弧，即一条直线如果满足：①AB 经过圆心O 且与圆交于A 、B 两点；②AB ⊥CD 交CD 于E ；那么可以推出：③CE ＝DE ；④CB ︵＝DB ︵；⑤CA ︵＝DA ︵.2.平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.(二)自学反馈1.如图，弦AB ⊥直径CD 于E ，相等的线段有：AE ＝EB ，CO ＝DO ；相等的弧有：AD ︵＝DB ︵，AC ︵＝BC ︵，CAD ︵＝CBD ︵.2.在⊙O 中，直径为10 cm ，圆心O 到AB 的距离OC 为3 cm ，则弦AB 的长为8_cm .活动1 小组讨论例 如图，一条公路的转弯处是一段圆弧(即图中CD ︵，点O 是CD ︵所在圆的圆心)，其中CD ＝600 m ，E 为CD ︵上一点，且OE ⊥CD ，垂足为F ，EF ＝90 m ，求这段弯路的半径.解：连接OC .设弯路的半径为R m ，则OF ＝(R －90)m .∵OE ⊥CD ，∴CF ＝12CD ＝12×600＝300(m ).在Rt △OCF 中，根据勾股定理，得OC 2＝CF 2＋OF 2，即R 2＝3002＋(R －90)2.解得R ＝545.所以，这段弯路的半径为545 m .常用辅助线：连接半径，由半径、半弦、弦心距构造直角三角形.活动2 跟踪训练1.如图，在⊙O 中，弦AB ＝4 cm ，点O 到AB 的距离OC 的长是2 3 cm ，则⊙O 的半径是4_cm .2.CD 是⊙O 的直径，AB 是弦，且AB ⊥CD ，垂足是E ，如果CE ＝2、AB ＝8，那么ED ＝8，⊙O 的半径r ＝5.3.已知：如图，线段AB 与⊙O 交于C 、D 两点，且OA ＝OB .求证：AC ＝BD .证明：作OE⊥AB于E.则CE＝DE.∵OA＝OB，OE⊥AB，∴AE＝BE.∴AE－CE＝BE－DE，即AC＝BD.活动3解决提出的问题即求出赵洲桥主桥拱的半径解决弦时常用的辅助线：过圆心作弦的垂线、连半径等构造直角三角形，根据垂径定理、勾股定理可解决：弦长、半径、弦心距、弓形高。