52第5章第2节区间估计
- 格式:ppt
- 大小:805.00 KB
- 文档页数:19

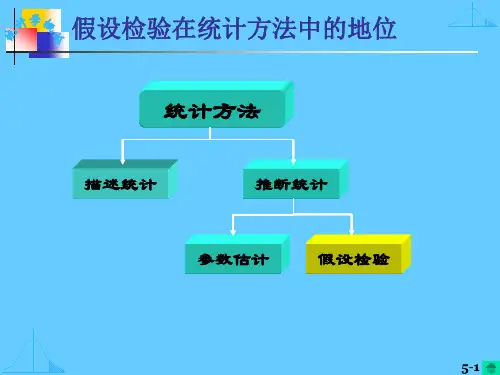




(1) P值是:1) 一种概率,一种在原假设为真的前提下出现观察样本以及更极端情况的概率。
2) 拒绝原假设的最小显著性水平。
3) 观察到的(实例的) 显著性水平。
4) 表示对原假设的支持程度,是用于确定是否应该拒绝原假设的另一种方法。
(2) P 值的计算:一般地,用X 表示检验的统计量,当H0 为真时,可由样本数据计算出该统计量的值C ,根据检验统计量X 的具体分布,可求出P 值。
具体地说:左侧检验的P 值为检验统计量X 小于样本统计值C 的概率,即:P = P{ X < C}右侧检验的P 值为检验统计量X 大于样本统计值C 的概率:P = P{ X > C}双侧检验的P 值为检验统计量X 落在样本统计值C 为端点的尾部区域内的概率的2 倍: P = 2P{ X > C} (当C位于分布曲线的右端时) 或P = 2P{ X< C} (当C 位于分布曲线的左端时) 。
若X 服从正态分布和t分布,其分布曲线是关于纵轴对称的,故其P 值可表示为P = P{| X| > C} 。
计算出P 值后,将给定的显著性水平α与P 值比较,就可作出检验的结论:如果α > P 值,则在显著性水平α下拒绝原假设。
如果α ≤ P 值,则在显著性水平α下接受原假设。
在实践中,当α = P 值时,也即统计量的值C 刚好等于临界值,为慎重起见,可增加样本容量,重新进行抽样检验。
整理自:区间估计区间估计(Interval Estimation)[编辑]什么是区间估计区间估计就是以一定的概率保证估计包含总体参数的一个值域,即根据样本指标和抽样平均误差推断总体指标的可能范围。
它包括两部分内容:一是这一可能范围的大小;二是总体指标落在这个可能范围内的概率。
区间估计既说清估计结果的准确程度,又同时表明这个估计结果的可靠程度,所以区间估计是比较科学的。
用样本指标来估计总体指标,要达到100%的准确而没有任何误差,几乎是不可能的,所以在估计总体指标时就必须同时考虑估计误差的大小。

(二)区间估计区间估计是指用样本指标、抽样误差和概率所构造的区间以估计总体指标存在的可能范围。
在进行区间估计的时候,根据所给定的条件不同,总体平均数和总体成数的估计有两条模式可供选择: 第一套:给定置信度要求,去推算抽样误差的可能范围。
第二套:根据已给定的抽样误差范围,求出概率保证程度。
1. 总体平均数的区间估计按照第一套模式,根据置信度F t ()的要求,估计极限抽样误差的可能范围)(∆∆∆或p x ,并指出估计区间(置信区间)。
具体步骤是:(1)抽取样本,并根据调查所得的样本单位标志值,计算样本平均数x ;计算样本标准差;在大样本下用以代替总体标准差推算抽样平均误差μ。
(2)根据给定的置信度F t ()的要求,查《正态分布概率表》,求得概率度t 值。
(3)根据概率度t 和抽样平均误差μx 计算极限抽样误差的可能范围μxx t =∆,并据以计算置信区间的上下限。
例14 麦当劳餐馆在7周内抽查49位顾客的消费额(元)如下,求在概率95%的保证下,顾客平均消费额的置信区间。
15 24 38 26 30 42 1830 25 26 34 44 20 3524 26 34 48 18 28 4619 30 36 42 24 32 4536 21 47 26 28 31 4245 36 24 28 27 32 3647 35 22 24 32 46 26第一步:根据样本计算样本平均数和标准差:x x n ==∑32 (元) S n x x ==-∑2945().(元),用样本标准差代替总体标准差σ=945.(元) 样本平均误差 x n μσ===94549135..(元)第二步:根据给定的置信度F t ()=95%,查概率表得t =196. 第三步:根据概率度t 和抽样平均误差推算抽样极限误差的可能范围。
65.235.196.1=⨯==∆μxx t (元) 将μxx ,的值代入区间估计公式 )(65.34)(35.2965.23265.232元元≤≤+≤≤-+≤≤-∆∆X X x X x xx计算结果表明,以95%的概率保证,麦当劳餐馆顾客消费额在29.35~34.65元之间。


数理统计与数据分析第三版答案第一章简介1.1 概述本章主要介绍了数理统计与数据分析的基本概念和作用。
数理统计是对数据进行收集、整理和分析的方法,数据分析则是从数据中提取有用的信息和结论。
1.2 数理统计的基本概念与分析步骤数理统计的基本概念包括总体、样本、参数和统计量等。
分析步骤包括收集数据、描述性统计、概率分布、参数估计和假设检验等。
1.3 数据分析的基本方法数据分析的基本方法包括描述统计和推断统计。
描述统计主要是对数据的总体特征进行描述,推断统计则是通过样本数据对总体进行推断。
第二章概率分布2.1 离散型随机变量离散型随机变量是在有限个或可列无限个数值中取值的随机变量。
本节介绍了离散型随机变量的概率质量函数、分布函数、期望和方差等。
2.2 连续型随机变量连续型随机变量是在某个区间内取值的随机变量。
本节介绍了连续型随机变量的概率密度函数、分布函数、期望和方差等。
第三章参数估计3.1 点估计点估计是用样本数据估计总体参数的方法。
本节介绍了点估计的基本原理和常用的点估计方法,包括最大似然估计和矩估计。
3.2 区间估计区间估计是通过样本数据估计总体参数的范围。
本节介绍了区间估计的基本原理和常用的区间估计方法,包括置信区间和预测区间。
第四章假设检验4.1 基本概念假设检验是用样本数据对总体参数的假设进行检验的方法。
本节介绍了假设检验的基本概念,包括原假设、备择假设、显著性水平和拒绝域等。
4.2 单样本均值检验单样本均值检验是对总体均值是否等于某个给定值进行检验的方法。
本节介绍了单样本均值检验的假设检验步骤和常用的检验方法,包括正态总体和非正态总体的检验。
第五章方差分析5.1 单因素方差分析单因素方差分析是对一个因素的影响进行分析的方法。
本节介绍了单因素方差分析的基本原理和常用的分析方法,包括单因素方差分析的假设检验和效应大小的度量。
5.2 多因素方差分析多因素方差分析是对多个因素的交互作用进行分析的方法。


第五章抽样调查及参数估计5.1 抽样与抽样分布5.2 参数估计的基本方法5.3 总体均值的区间估计5.4 总体比例的区间估计5.5 样本容量的确定一、简答题1.什么是抽样推断?用样本指标估计总体指标应该满足哪三个标准才能被认为是优良的估计?2.什么是抽样误差,影响抽样误差的主要因素有哪些?3.简述概率抽样的五种方式二、填空题1.抽样推断是在随机抽样的基础上,利用样本资料计算样本指标,并据以推算总体数量特征的一种统计分析方法。
2.从全部总体单位中随机抽选样本单位的方法有两种,即重复抽样和不重复抽样。
3.常用的抽样组织形式有简单随机抽样、类型抽样、等距抽样、整群抽样等四种。
4.影响抽样误差大小的因素有总体各单位标志值的差异程度、抽样单位数的多少、抽样方法和抽样调查的组织形式。
5.总体参数区间估计必须具备估计值、概率保证程度或概率度、抽样极限误差等三个要素。
6.从总体单位数为N的总体中抽取容量为n的样本,在重复抽样和不重复抽样条件下,可能的样本个数分别是______________和_____________。
7.简单随机_抽样是最基本的抽样组织方式,也是其他复杂抽样设计的基础。
8.影响样本容量的主要因素包括总体各单位标志变异程度_、__允许的极限误差Δ的大小、_抽样方法_、抽样方式、抽样推断的可靠程度F(t)的大小等。
三、选择题1.抽样调查需要遵守的基本原则是( B )。
A.准确性原则 B.随机性原则 C.代表性原则 D.可靠性原则2.抽样调查的主要目的是( A )。
A.用样本指标推断总体指标 B.用总体指标推断样本指标C.弥补普查资料的不足 D.节约经费开支3.抽样平均误差反映了样本指标与总体指标之间的( B )。
A.实际误差 B.实际误差的平均数C.可能的误差范围 D.实际的误差范围4.对某种连续生产的产品进行质量检验,要求每隔一小时抽出10分钟的产品进行检验,这种抽查方式是( D )。
A.简单随机抽样 B.类型抽样 C.等距抽样 D.整群抽样5.在其他情况一定的情况下,样本单位数与抽样误差之间的关系是( B )。
关于区间估计的课程设计一、课程目标知识目标:1. 学生能够理解区间估计的基本概念,掌握其定义和性质。
2. 学生能够运用区间估计方法,对总体参数进行估计,并解释估计结果的含义。
3. 学生能够掌握区间估计的误差分析,了解影响区间估计精度的因素。
技能目标:1. 学生能够运用统计软件或计算器进行区间估计的计算。
2. 学生能够根据实际问题,选择合适的区间估计方法,并解决实际问题。
3. 学生能够通过实例分析,提高数据处理和分析能力。
情感态度价值观目标:1. 学生能够认识到统计学在实际生活中的广泛应用,增强学习统计学的兴趣。
2. 学生能够培养严谨的科学态度,注重数据分析的客观性和准确性。
3. 学生能够通过小组合作,培养团队协作能力和沟通表达能力。
课程性质分析:本课程为高中统计学课程,旨在帮助学生掌握区间估计的基本方法,提高数据处理和分析能力。
学生特点分析:高中学生具备一定的数学基础和逻辑思维能力,但对于统计学方法的应用还较为陌生,需要通过实例和实际操作来加深理解。
教学要求:1. 注重理论与实践相结合,让学生在实际问题中感受区间估计的应用价值。
2. 强调计算能力的培养,引导学生熟练使用统计软件或计算器进行计算。
3. 鼓励学生积极参与讨论和分享,提高课堂互动效果。
二、教学内容1. 区间估计基本概念:总体参数、样本统计量、估计量、置信区间。
2. 区间估计的原理与方法:中心极限定理、标准误差、正态分布的性质。
3. 置信区间的计算与应用:- 单个总体均值的区间估计。
- 单个总体比例的区间估计。
- 两个总体均值差的区间估计。
- 两个总体比例差的区间估计。
4. 影响区间估计精度的因素:样本容量、总体标准差、置信水平。
5. 实际问题中的应用:分析实际问题,选择合适的区间估计方法,解决实际问题。
教学大纲安排:第一课时:区间估计基本概念,总体参数与样本统计量。
第二课时:中心极限定理,标准误差,正态分布性质。
第三课时:单个总体均值和比例的区间估计。
关于区间估计的课程设计一、课程目标知识目标:1. 学生能够理解区间估计的基本概念,掌握其定义及作用;2. 学生能够掌握计算置信区间的公式,并能够运用到实际问题中;3. 学生能够了解置信区间的性质,如包含概率、置信水平等。
技能目标:1. 学生能够运用所学的区间估计方法,对给定的数据进行估计,并解释结果;2. 学生能够运用统计软件或计算器进行区间估计的计算,提高数据处理能力;3. 学生能够通过实例分析,培养解决实际问题时运用区间估计的能力。
情感态度价值观目标:1. 学生能够认识到统计学在生活中的广泛应用,激发对统计学学习的兴趣;2. 学生能够通过小组合作,培养团队协作能力和沟通表达能力;3. 学生能够理解数据不确定性,培养科学、严谨的思维方式,提高解决问题的信心。
分析课程性质、学生特点和教学要求,本课程目标旨在帮助学生掌握区间估计的基本概念和计算方法,培养学生运用统计学知识解决实际问题的能力。
课程目标具体、可衡量,以便教师进行教学设计和评估,确保学生在本章节学习中取得预期成果。
二、教学内容本章节教学内容主要包括以下几部分:1. 区间估计的基本概念:- 定义及作用- 置信区间的理解2. 置信区间的计算方法:- 样本均值和方差的置信区间- 不同分布下的置信区间计算3. 置信区间的性质:- 包含概率- 置信水平- 置信区间的宽度4. 区间估计在实际问题中的应用:- 实例分析- 统计软件或计算器的使用5. 教学内容的安排与进度:- 第一节课:区间估计的基本概念及置信区间的定义- 第二节课:置信区间的计算方法及性质- 第三节课:实际问题中的应用及实例分析教学内容参考教材相关章节,结合课程目标进行系统组织。
通过以上教学内容的学习,使学生能够掌握区间估计的基本知识,培养解决实际问题的能力,同时注重理论与实践相结合,提高学生的统计学素养。
三、教学方法针对本章节内容,采用以下多样化的教学方法,以激发学生的学习兴趣和主动性:1. 讲授法:- 对区间估计的基本概念、性质和计算方法进行系统讲解,使学生建立完整的知识结构;- 结合实际案例,讲解区间估计在统计学中的应用,提高学生的实际运用能力。